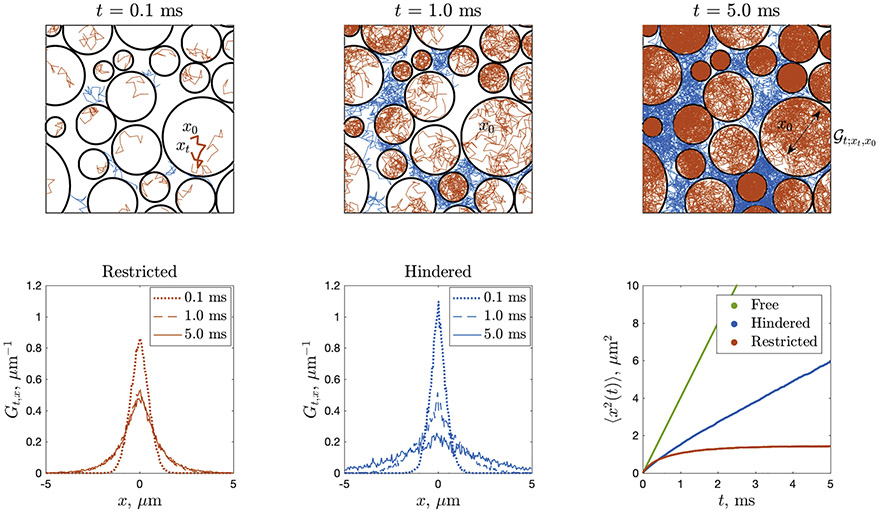
Fig. 1.

dMRI propagator G_t,x, Eq. (2), as an ensemble-average of the local diffusion propagator ${\mathcal{G}}_{t;x_t,x_0}$ (see text), here sampled using Monte Carlo (MC) simulations in the geometry of non-overlapping impermeable circular “cells” of diameters 0.35–6.25 μm. The intra-cellular (restricted) ${\mathcal{G}}_{t;x_t,x_0}$, sampled by red MC paths, for long enough t fills up each cell, such that the net restricted contribution G_t,x averaged over all red paths remains non-Gaussian, as shown in bottom-left panel (G_t,x is bounded in x, and it becomes t-independent practically after t ≳ 1ms, with a bounded variance (1) plotted in bottom-right panel). The extra-cellular (hindered) ${\mathcal{G}}_{t;x_t,x_0}$, sampled by blue MC paths, is allowed to spread infinitely far, hence its ensemble-average G_t;x asymptotically spreads as a Gaussian with variance growing asymptotically linearly with t, Eq. (1), with the slope D(t)∣_t→∞ = D_∞ < D₀. Bottom-left and middle panels show the ensemble-averaged propagator projected onto the x-axis, by integrating the displacements along the y-axis. Bottom-right panel also shows Eq. (1) for the free diffusion, with D = D₀, as a reference. Most of the information about cell sizes, shapes and their packing is washed out after the ensemble averaging. Figure courtesy of Lee (2019).