FIGURE 1.

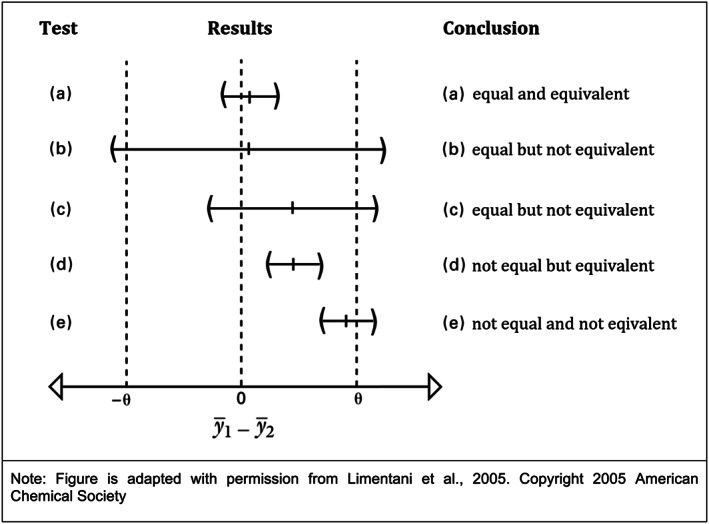
Equivalence testing versus difference testing. For testing equivalence, a reversal of the traditional null and alternative hypotheses is required, such that we can then demonstrate equivalence that is statistically significant, practical, and precise. The “two‐sided equivalence test” (TOST), designed specifically for equivalence testing, begins with a null hypothesis that the two mean values are not equivalent, then attempts to demonstrate that they are equivalent (or “similar”) within an a priori determined “equivalence interval” that provides evidence of statistically significant equivalence or similarity. Unlike the two‐sample t‐test, TOST penalizes poor precision and/or small n values and places the burden on the analyst to prove that the parameters are equivalent. The figure below, adapted with permission from Limentani et al. (2005), illustrates the differences between the conclusions one can draw from the traditional t‐test versus those from an equivalence test, based on confidence intervals for mean difference ${\overline{y}}_1-{\overline{y}}_2$, and equivalence interval ±θ