Deformation Aware Augmented Reality for Craniotomy using 3D/2D Non-rigid Registration of Cortical Vessels

Abstract

Intra-operative brain shift is a well-known phenomenon that describes non-rigid deformation of brain tissues due to gravity and loss of cerebrospinal fluid among other phenomena. This has a negative influence on surgical outcome that is often based on pre-operative planning where the brain shift is not considered. We present a novel brain-shift aware Augmented Reality method to align pre-operative 3D data onto the deformed brain surface viewed through a surgical microscope. We formulate our non-rigid registration as a Shape-from-Template problem. A pre-operative 3D wire-like deformable model is registered onto a single 2D image of the cortical vessels, which is automatically segmented. This 3D/2D registration drives the underlying brain structures, such as tumors, and compensates for the brain shift in sub-cortical regions. We evaluated our approach on simulated and real data composed of 6 patients. It achieved good quantitative and qualitative results making it suitable for neurosurgical guidance.

1. Introduction

Brain shift is a well-known intra-operative phenomenon that occurs during neurosurgical procedures. This phenomenon consists of deformation of the brain that changes the location of structures of interest from their locations in pre-operative imaging [2] [17]. Neurosurgical procedures are often based on pre-operative planning. Therefore, estimating intra-operative brain shift is important since it may considerably impact the surgical outcome. Many approaches have been investigated to compensate for brain shift, either using additional intra-operative imaging data [14] [20] [11] [21] or advanced brain models to predict intra-operative outcome pre-operatively [3] [8] [7]. The latter approach has the advantage of being hardware-independent and does not involve additional imaging in the operating room. However, even sophisticated brain models have difficulty modeling events that occur during the procedure. Additional data acquisition is then necessary to obtain a precise brain shift estimation. Various types of imaging techniques have been proposed to acquire intra-operative information such as ultra-sound [11] [21] [20], Cone-Beam Computed Tomography [19] or intra-operative MRI [14].

During a craniotomy, the cortical brain surface is revealed and can be used as an additional source of information. Filipe et al. [16] used 3 Near-Infrared cameras to capture brain surface displacement which is then registered to MRI scans using the coherent point drift method by considering vessel centerlines as strong matching features. A new deformed MRI volume is generated using a thin plate spline model. The approach presented by Luo et al. [15] uses an optically tracked stylus to identify cortical surface vessel features; a model-based workflow is then used to estimate brain shift correction from these features after a dural opening. Jiang et al. [12] use phase-shifted 3D measurement to capture 3D brain surface deformations. This method highlights the importance of using cortical vessels and sulci to obtain robust results. The presence of a stereo-miscroscope in the operating room makes it very convenient to deploy such methods clinically. Sun et al. [23] proposed to pre-compute brain deformations to build an atlas from a sparse set if image-points extracted from the cortical brain surface. These image-points are extracted using an optically tracked portable laser range scanner. Haouchine et al. [9] proposed to use a finite element model of the brain shift to propagate cortical deformation captured from the stereoscope to substructures. In a similar way Mohammadi et al. [18] proposed a projection-based stereovision process to map brain surface with a pre-operative finite element model. A pre-defined pattern is used to recover the 3D brain surface. In order to build a dense brain surface and gather more precise positions, Ji et al. [10] proposed a stereo-based optical flow shape reconstruction. The 3D shapes are recovered at different surgical stages to obtain undeformed and deformed surfaces. These surfaces can be registered to determine the deformation of the exposed brain surface during surgery.

Contribution: We propose a novel method to register pre-operative scans onto intra-operative images of the brain surface during the craniotomy. As shown in the pipeline of figure 1, our method uses images from a surgical microscope (or possibly a ceiling mounted camera), rather than intra-operative ultrasound or MRI which requires significant cost and time. Unlike previous methods, we rely solely on a single image to avoid tedious calibration of the stereo camera, laser range finder or optical stylus. Our method considers cortical vessels centerlines as strong features to drive the non-rigid registration. The intra-operative centerlines are automatically extracted from the image using convolutional deep neural networks, while the pre-operative centerlines are modelled as a network of linked beams capable of handling non-linear deformations. Our approach is formulated as a force-based shape-from-template problem to register the undeformed pre-operative 3D centerlines onto the deformed intra-operative 2D centerlines. This problem is solved by satisfying a combination of physical and projective constraints. We present our results through the microscope occulars using Augmented Reality view by overlaying the tumor model in the miscropcic view after accounting for the estimated brain shift deformation.

Fig. 1:

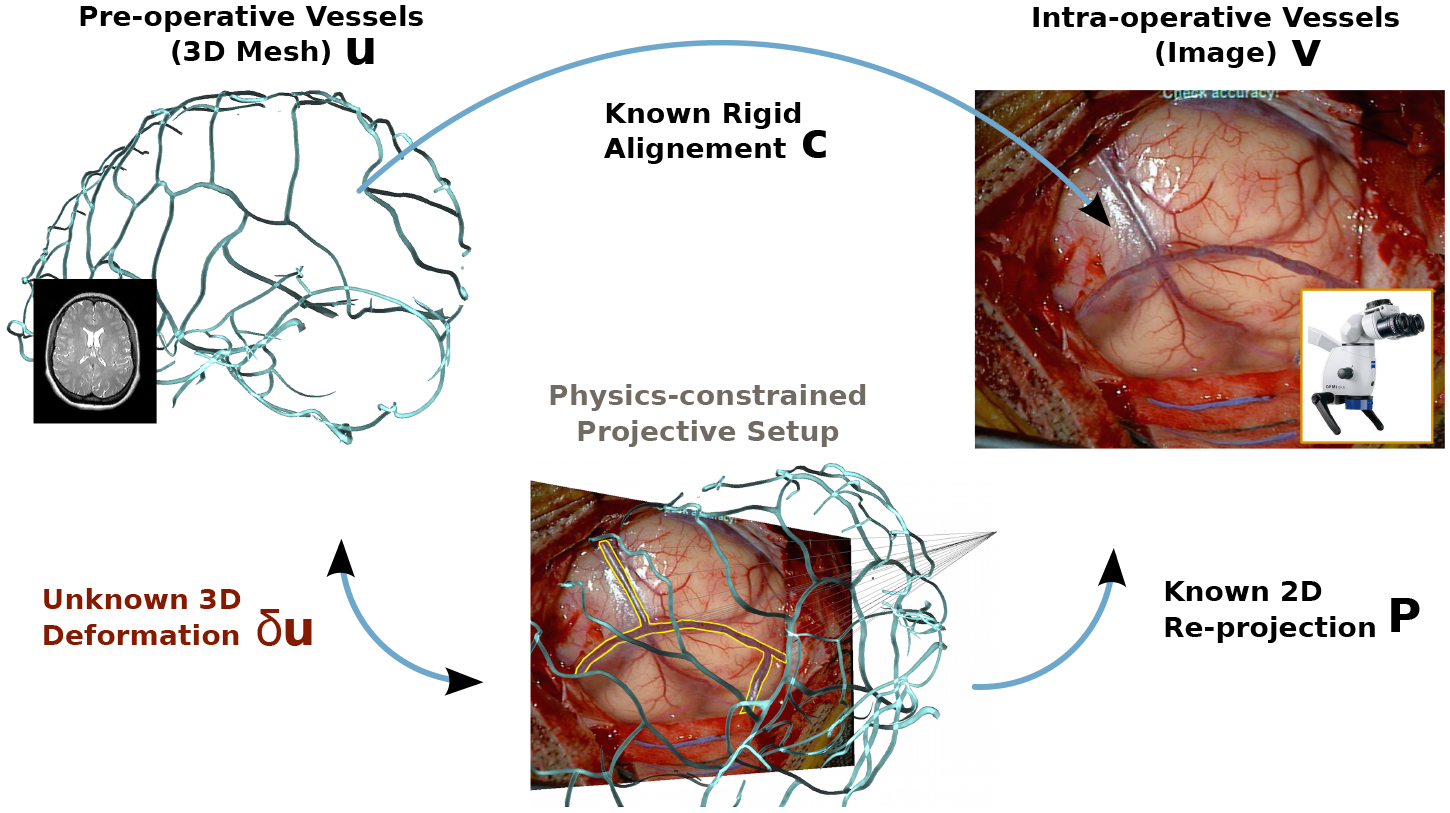
Problem formulation: we aim at recovering the deformed 3D vessels shape δu from its known reprojection in the image v, the known pre-operative 3D vessels at rest u and known rigid alignment c, satisfying physical and reprojective constraints P.

2. Method

2.1. Extracting 2D Cortical Brain Vessels

To extract the vessels from microscopic images we rely on a deep convolutional network following a typical U-Net architecture [22]. The input is a single RGB image of size 256 × 256 × 3 and the final layer is a pixel-wise Softmax classifier that predicts a class label {0, 1} for each pixel. The output image is represented as a binary image of size 256 × 256 as illustrated in Figure 2. the segmentation can suffer from class imbalance because microsopic images of the cortical surface are composed of veins, arteries and parenchyma of different sizes. We thus rely on a weighted cross-entropy loss L to account for imbalanced depths [6], formulated as follows:

$$L=-\frac{1}{n}\sum _i{w}_{c_i}\cdot c_i^{*}\cdot log\left(c_i\right)\mathit{\text{ with }}{c}_i=\frac{e^{z_i}}{{\sum }_c{e}^{z_i,c_i}}and{w}_{c_i}=\frac{\text{med}\left(f_{c_i}\mid c_i\in C\right)}{f_{c_i}}$$ (1)

where n is the number of pixels, C is the set of classes, $c_i^{*}$ is the ground truth label of pixel i, c_i is the probability of classifying pixel i with class c_i. (z_i, c_i) is the output of the response map and $w_{c_i}$ is the class-balanced weight for class c_i, with $f_{c_i}$ being the frequencies of class c_i and med(·) the median. Once segmented, the vessel centerlines are extracted from the binary image by skeletonization. We denote v, the vector of 2D points corresponding to the intra-operative centerlines.

Fig. 2:

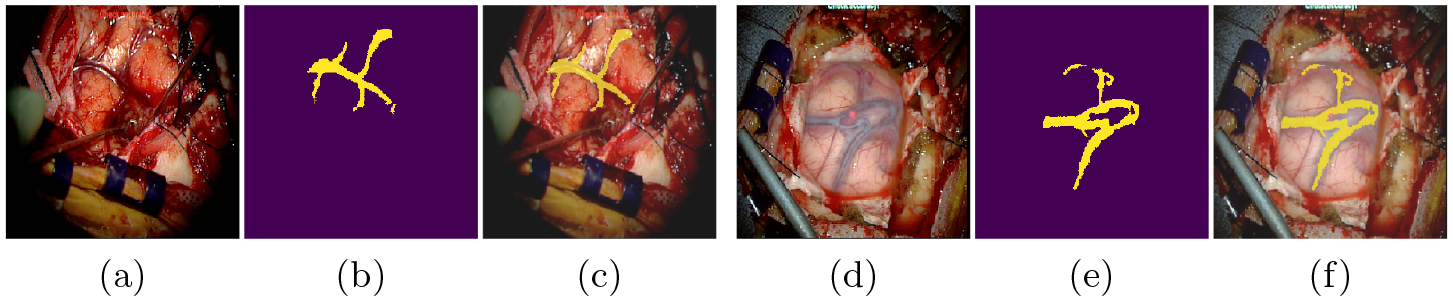
Extracting 2D cortical brain vessels: A classical U-Net architecture is used to segment the microscopic images. The input images (a) or (d) are segmented to obtain a binary image (b) or (e). The images (c) and (f) consist of overlays.

2.2. 3D Vascular Network Modelling

Let us denote u the vector of 3D vertices representing the vessel centerlines derived from MRI scans. This set of vertices is used to build a non-rigid wire-like model that represents the behaviour of cortical vessels. More precisely, the vessels are modeled with serially linked beam elements that can handle geometric non-linearities while maintaining real-time computation. This model has previously been used to simulate guide wires and catheters [4]. Each beam element is delimited by two nodes each having 3 spatial and angular degrees of freedom. These node positions relate to the forces applied to them thanks to a stiffness matrix K_e and account for rotational degrees of freedom through a rotational matrix R_e. At each node i, the internal forces f_i generated by the deformation of the structures is formulated as:

$$f_i=\sum _{e=i-1}^i{R}_e(u)K_e\left(R_e{(u)}^T\left(u-u_e\right)-u^{\mathit{\text{rest}}}\right)$$ (2)

where e is the index of the two beams connected to this i^th node. u_i−1, u_i and u_i+1 are the degrees of freedom vectors of the three nodes (respectively i − 1, i, i + 1) and belong to the two beams in the global frame. u_ej denotes the middle frame of the j^th beam that is computed as an intermediate between the two nodes of the beam, where u^rest corresponds to the degrees of freedom at rest in the local frame. The global force f emanating from the 3D vessels can be computed as $f={\sum }_j^{n_u}{f}_j$, with n_u being the number of nodes of the vascular tree.

2.3. Force-based Shape-from-Template

A shape-from-template problem is defined as finding a 3D deformed shape from a single projected view knowing the 3D shape in rest configuration [1]. In our case, the 3D shape at rest consists of the pre-operative 3D centerlines u. The single projected view consists of the 2D intra-operative centerlines v. The unknown 3D deformed shape δu is the displacement field induced by a potential brain shift. As in most registration methods, an initial set of n_c correspondences c between the image points and the model points has to be established. We thus initialise our non-rigid registration with a rough manual rigid alignment. Once aligned, a vector c is built so that if a 2D point v_i corresponds to a 3D point u_j then c_i = j for each point of the two sets. Assuming that the camera projection matrix P is known and remains constant, registering the 3D vessels to their corresponding 2D projections amounts to minimize the re-projection error $\Vert P{u}_{c_i}-v_i\Vert$ for i ∈ n_c. However, minimizing this error does not necessarily produces a correct 3D representation since many 3D shapes may have identical 2D projections. To overcome this issue, we add to the re-projection constraints the vessels’ physical priors following the beams model introduced in Eq. 2. This will force the shape of the vascular tree to remain consistent in 3D while minimizing the reprojection error in 2D. This leads to the following force minimization expression:

$$\underset{\delta u}{\text{argmin}}\sum _i^{n_c}{\left(f_{c_i}-\kappa \Vert P{u}_{c_i}-v_i\Vert \right)}^2$$ (3)

where κ is the stiffness coefficient that permits the image re-projection error to be translated to an image bending force. Note the subscript c_i that denotes the correspondence indices between the two point sets. This minimization can be seen as enforcing 3D vessel centerlines to fit sightlines from the camera position to 2D vessels centerlines while maintaining a coherent 3D shape.

2.4. Mapping Tumors with Cortical Vessels Deformation

In order to propagate the surface deformation to tumors and other sub-cortical structures, we use a linear geometrical barycentric mapping function. We restrict the impact of the cortical vessel deformations to the immediate underlying structures (see Figure 6).

Fig. 6:

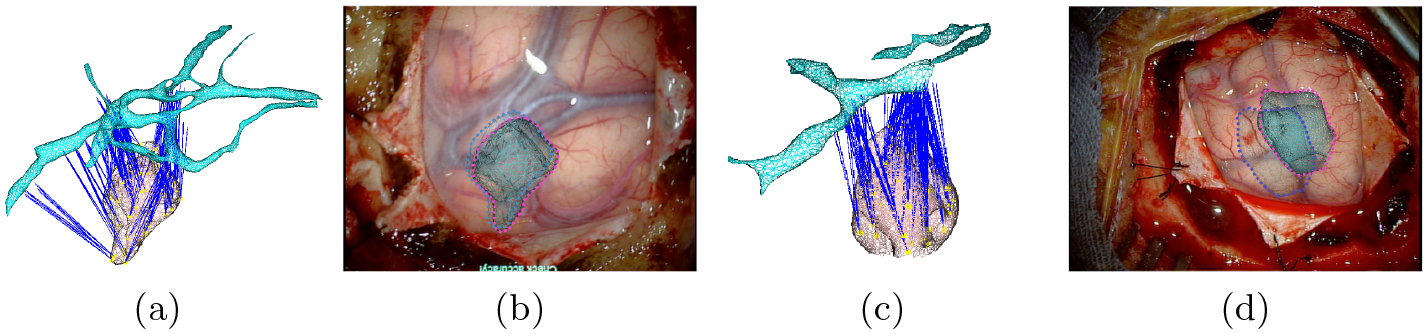
Mapping tumors with cortical vessels: In (a) and (c), a visualization of the mapping mechanism. Blue lines represent the attachments. In (b) and (d), an Augmented Reality visualization of the tumors with the estimate displacement induced from the mapping w.r.t to initial positions (dotted blue lines).

Formally speaking, if we denote the vector of vertices representing a 3D tumor by t, we can express each vertex t_i using barycentric coordinates of facet vertices u, such that $t_i={\sum }_{j=1}^3{\varphi }_j\left(x_i,y_i,z_i\right)u_j$, where ϕ(x, y, z) = a + bx + cy with (a, b, c) being the barycentric coordinates of the triangle composed of nodal points u_j, with 1 ≤ j ≤ 3. This mapping is computed at rest and remains valid during the deformation.

3. Results

We tested our method on simulated data of a 3D synthetic human brain. The 3D vessel centerlines were extracted from the vessels mesh surface using a mean curvature skeletonization technique. The number of centerline nodes to build the wire-like model is set in a range between 12 and 30 nodes (only a subset of the vascular network has been considered). The stiffness matrix of the vessels is built with a Young’s modulus set to 0.6 MPa and Poisson’s ratio to 0.45 to simulate a quasi-elastic and incomprehensible behaviour where vessels thickness is set to 0.5 mm [5]. We used the Sofa framework (www.sofa-framework.org) to build the 3D beam-elements model.

We quantitatively evaluated our method by measuring the target registration error (TRE) on different locations. We considered four in-depth locations from 0 mm to 45 mm, 0 mm being the cortical surface. We simulated a brain shift to mimic a protrusion deformation that can occur due to brain swelling after the craniotomy. The deformations were of increasing amplitudes: Def1 = 1.7 mm, Def2 = 4 mm, Def3 = 6 mm and Def4 = 10 mm. We extracted 2D centerlines of each deformation by projecting the deformed 3D centerlines w.r.t a known virtual camera. We added Gaussian noise with a standard deviation of 5 mm and a 5 clustering decimation on the set of 2D points composing the centerlines. The results reported in Figure 3 suggest that using our method achieves small TRE ranging from 0.53 mm to 1.93 mm, on the cortical surface and the immediate sub-cortical structures (≤ 15 mm). Since the TRE depends on the amount of brain shift, we also quantify the brain-shift compensation by measuring the difference between the initial and the corrected error (normalized by the initial error). Brain shift compensation of up to 68.2 % is achieved, and at least a 24.6 % compensation is reported for the worst configuration. We can also observe that errors and compensation at the cortical surface are very close to the immediate sub-cortical location (≤ 15 mm). They increase when the targets are located deeper in the brain (≥ 30 mm) or the amount of deformation increases (≥ 6 mm).

Fig. 3:

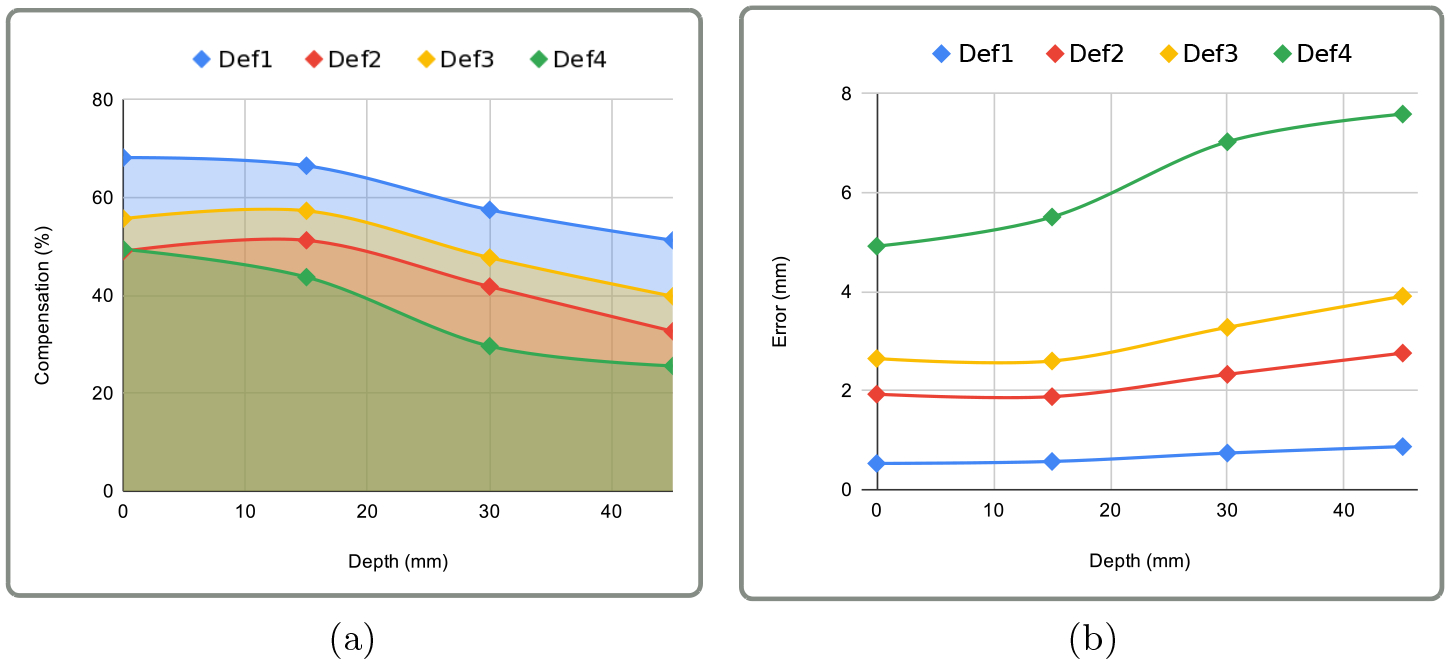
Quantitative evaluation on simulated data: Charts (a) and (b) show the percentage of compensation and target registration error respectively w.r.t to depth and brain shift amplitude. The depth axis correspond to the position of the target in the brain where 0mm represent the cortical surface and 45mm the deep brain.

Our craniotomy dataset was composed of 1630 microscopic image patches with labels obtained through manual segmentation. The model is trained on mini-batches of size 32 for 200 epochs using Adam optimizer [13] with a learning rate of 0.001 that is decreased by a factor of 10 each 100 epochs. We used the Tensorflow framework (www.tensorflow.org) on an NVidia GeForce GTX 1070.

We tested our method on 6 patient data sets retrospectively. The cortical vessels, brain parenchyma, skull and tumors were segmented using 3D Slicer (www.sliced.org). The miscroscopic images were acquired with a Carl Zeiss surgical microscope. We only used the left image of the sterescopic camera.

The pre-operative vessels are first aligned manually on the image to obtain the rigid transform, then the 3D/2D non-rigid registration was performed, and used to drive deformation of the underlying tumors. Figure 4 shows the resulting Augmented Reality rendering and exhibits good mesh-to-image overlay. Figure 5 shows the measured deformation amplitude on each vessel after non-rigid registration. The deformations range from 0 to 3 mm and are non-uniformly distributed on the vascular trees which suggest a non-rigid deformation.

Fig. 4:

Augmented Reality views after applying our method on 6 patient data sets retrospectively. The non-rigid registration provided a good estimation of deformation of the cortical surface, as viewed by overlays of the deformed 3D vessels on their 2D projections seen through the surgical microscope.

Fig. 5:

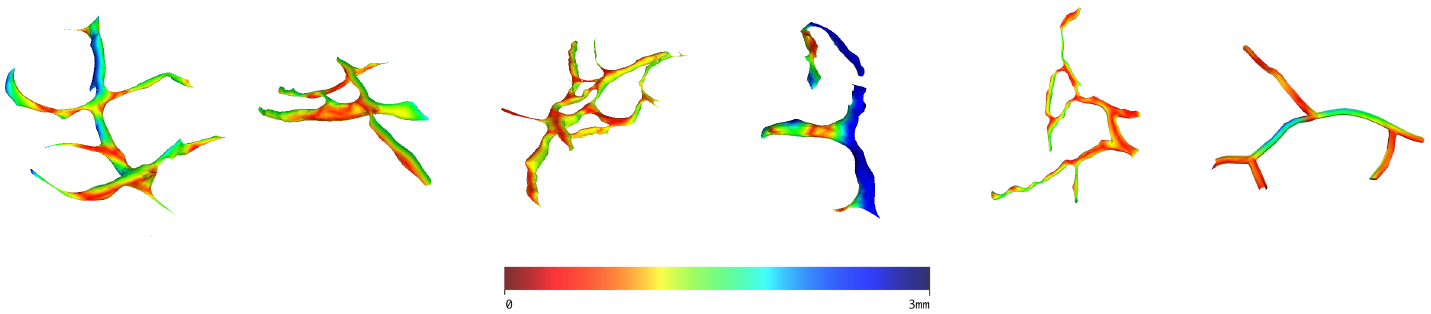
Color-coded estimated deformation on the vessels.

Finally, we show in Figure 6 the ability of our method to rectify tumor positions through their mapping with the cortical vessels. We can clearly see that tumor positions are corrected according to the brain shift estimated from the cortical vessels registration.

4. Conclusion and Discussion

We proposed here a brain-shift aware Augmented Reality method for craniotomy guidance. Our method follows a 3D/2D non-rigid process between pre-operative and intra-operative cortical vessel centerlines using a single image instead of a stereo pair. Restricting our method to a single image makes it more acceptable in operating rooms but turns the registration process into an ill-posed problem. To tackle this issue we proposed a force-based shape-from-template formulation that adds physical constraints to the classical reprojection minimization. In addition, our pipeline takes advantage of recent advances in deep learning to automatically extract vessels from microscopic images. Our results show that low TRE can be obtained at cortical and sub-cortical levels and compensation for brain shift with up to 68% can be achieved. Our method is however sensitive to the outcome of the cortical vessels segmentation. A fragmented segmentation may lead to discontinuous centerlines and thus produce aberrant vascular trees that can affect the whole pipeline. One solution could be the use of the complete vessels segmentation in addition to centerlines to make advantage of the use of more featured such as radii, curves and bifurcations. Future work will consist of developing a learning-based method to perform the non-rigid registration without manual initialisation, with the aim of facilitating its usage by surgeons in clinical routines.