Abstract
Since the first official case of COVID-19 was reported, many researchers around the world have spent their time trying to understand the dynamics of the virus by modeling and predicting the number of infected and deaths. The rapid spread and highly contagiousness motivate the necessity of monitoring cases in real-time, aiming to keep control of the epidemic. As pointed out by [3], some pitfalls like limited infrastructure, laboratory confirmation and logistical problems may cause reporting delay, leading to distortions of the real dynamics of the confirmed cases and deaths. The aim of this study is to propose a suitable statistical methodology for modeling and forecasting daily deaths and reported cases of COVID-19, considering key features as overdispersion of data and correction of notification delay. Both, reporting delays and forecasting consider a Bayesian approach in which the daily deaths and the confirmed cases are modelled using the negative binomial (NB) distribution in order to accommodate the population heterogeneity. For the correction of notification delay, the mean number of occurrences regarding time t notified at time (mean delayed notifications) is associated to the temporal and the delay lag evolution of the notification process through a log link. With regard to daily forecasting, the functional form adopted for the number of deaths and reported cases of COVID-19 is related to the sigmoid growth equation. A variable regarding week days or days off was considered in order to account for possible reduction of the records due to the lower offer of tests on days off. To illustrate the methodology, we analyze data of deaths and infected cases of COVID-19 in Espírito Santo, Brazil. We also obtain long-term predictions.
Keywords: COVID-19, Notification delay, Prediction, Overdispersion
1. Introduction
The new coronavirus (SARS-CoV-2) is contagious among humans and causes the COVID-19 disease. COVID-19 was firstly reported in December 2019 after the appearence of an unidentified pneumonia. In Brazil, the first confirmed case of infection by SARS-CoV-2 was reported by the Health Ministry on February 26, 2020. Subsequently, in March 2020, the World Health Organization (WHO) announced the COVID-19 as a pandemic because of the growing number of infected cases outside China, where the outbreak started. According to the reports of the panel at WHO (https://covid19.who.int/), in July 2020 there were more than 17 million cases of COVID-19, including near 700.000 deaths around the world, affecting more than 200 countries and territories. At the same month, official data in Brazil indicated approximately 2.5 million confirmed cases of COVID-19 and more than 90.000 deaths.
The severity of the COVID-19 range from mild to severe respiratory symptoms. Some researchers call attention to the existence of severe neurological complications [21]. Older people and people of any age with comorbidities (obesity, type 2 diabetes mellitus, serious heart conditions, etc.) present higher risks for severe illness, requiring hospitalization, intensive care and/or mechanical ventilation. The most serious cases of COVID-19 may lead to death.
As pointed out by [27], the virus has the potential to spread rapidly and infect a large fraction of the population, overwhelming health care systems. Given the rapid rate of spread, [27] suggest that a combination of control measures, including early and active surveillance, quarantine and especially strong social distancing efforts, is needed to slow down or stop the spread of the virus.
Unfortunately, the COVID-19 pandemic is evolving rapidly and is not only a medical emergency and public health tragedy, but it is also affecting economic activities. With no urgent actions, the socioeconomic effects could have wide implications for trade, travel, provision of aid, economic markets, supply chains and the daily lives of people living around the world [30]. As pointed out by [19], COVID-19 is a medical problem with immense societal consequences. The world's scientists need to come together to find the proper solution for controlling this pandemic event, manage its consequences, and prevent future recurrences of similar pandemics.
To prepare the health care system for COVID-19 patients, it is necessary to quickly identify cases and keep control of the epidemic. [3] discuss the difficulties in monitoring epidemics in real-time and indicate the reporting delay as a crucial issue because it distorts the relationship between the reported disease incidence and the true disease incidence. According to them, reporting delays may be due to laboratory confirmation, logistical problems, infrastructure difficulties, and so on.
Many institutions and research groups around the world are dedicated to modeling and prediction of the number of confirmed cases and deaths associated to COVID-19. Different methodologies have been considered for these purposes, as can be seen in [29], [20] and [22]. In [13], attention is drawn to the problem of collective dynamics in human populations in different scenarios, such as crowd disasters, crime, terrorism, war and disease spreading. The authors discuss the complexity to propose analytic and predictive models. Regarding global pandemics, [13] also present a history of the development of mathematical models in this context until nowadays, showing that, despite of challenges, complex science has produced major advances in modeling the dynamics of global epidemics and it includes quantitative, realistic, and even predictive models, bringing together statistical data analysis, modeling efforts, analytical approaches, and laboratory experiments. One of the most popular modeling strategies in this scenario is the use of compartmental models [6], [28], [15], [26], including the well-known SIR model and its extensions, such as the SEIR model [4], [10] and the SIDARTHE model [11], among others. Basically, SIR-type models partition the population in “compartments” and define a system of nonlinear ordinary differential equations describing the transitions among these groups, which must be solved numerically. An improvement of the SIR model, including more realistic assumptions such as the effect of births and deaths due to other causes is suggested by [1]. The research of [12] shows that a SEIR model underestimates peak infection rates and substantially overestimates epidemic persistence after the peak has passed. The mathematical structure of SIR model and a discussion about the limitation of the method in the literature is described by [8].
Regarding stochastic models, [31] provide an estimate of the size of the epidemic in Wuhan on the basis of the number of cases exported from Wuhan to cities outside mainland China and forecast the extent of the domestic and global public health risks of epidemics, accounting for social and non-pharmaceutical prevention interventions. For this, they consider a stochastic modelling in terms of the SEIR model with the basic reproductive number () being estimated using the Gibbs sampling and non-informative flat prior. The is defined by [7] as the average number of infectious contacts that an infected individual has before recovering and becoming immune (or dying). It is one of the most crucial quantities in infectious diseases and, as pointed out in [16], measures how contagious a disease is. For , the disease is expected to stop spreading, but for an infected individual can infect on an average 1 person, that is, the spread of the disease is stable. The disease can spread and become epidemic if . The nowcasting considered in [31] is related to the impact of the social distancing measures, use of face masks and improved personal hygiene and other in the transmissibility of the virus and not with the reporting delays as proposed by [3]. An extensive simulation of the epidemic forecasts for Wuhan and five other Chinese cities assuming that the transmissibility of SARS-CoV-2 was reduced by 0%, 25%, and 50% after Wuhan was quarantined on Jan 23, 2020 and with 0% and 50% mobility reduction inter-city was performed by [31].
In Brazil, [9] provides a web page and an app with daily updates of the number of infected people and deaths and also presents the short (1 to 2 weeks) and long term prediction for COVID-19. The statistical methodology considered by them is a hierarchical Bayesian model where the number of infected or deaths is modelled by a Poisson distribution with a time invariant non-linear predictor for the mean. A well known limitation of the Poisson distribution is the equidispersion, which intrinsically assumes that the mean and the variance of the response variable are equal. For many observed count data, it is common to identify overdispersion, which occurs when the sample variance is greater than the sample mean [14]. The simplest strategy to deal with overdispersion is to use the negative binomial regression and it is recommended when the extra variations presented on the data are caused by the heterogeneity of the population [5].
[7] show that the population heterogeneity can significantly impact the disease-induced immunity due to SARS-CoV-2 and argue that many SIR-type models assume a homogeneously mixing population in which all individuals are equally susceptible, and equally infectious if they become infected. The authors propose to accommodate this heterogeneity by categorizing the community into different age cohorts, with heterogeneous mixing between the different age cohorts, and their social active level.
From the previous discussion, the heterogeneity mentioned by [7] may induce overdispersion on COVID-19 data. In order to accommodate this phenomenon, we propose an extension of the model developed by [9], considering a negative binomial distribution instead of the Poisson. We have performed a reparameterization of the model in terms of more meaningfully quantities, allowing an easier prior elicitation. We have also incorporated other important features in the model. Specifically, we include an explanatory variable regarding week days and days off, in order to account for possible reduction of the records due to the lower offer of tests on days off, which, to the best of our knowledge, has not been considered in any mathematical or statistical analysis. We have also allowed time variation of the model parameters in order to account for the unstable nature of the pandemic.
We use data from Espírito Santo State in Brazil (ES/BR) to illustrate the proposed methodology. The purpose here is to predict the daily number of confirmed infections and deaths caused by COVID-19 for short and long term. Two main reasons have motivated us to analyze these data: (1) since 16/04/2020, the technical report of the non-governmental organization Open Knowledge Brasil (OKBR) identifies the state of ES/BR as one of the most transparent states in the dissemination of data regarding the COVID-19 in Brazil; (2) unlike most of the states in Brazil, the daily number of confirmed cases and deaths are aggregated at the date of occurrence (day of realization of the test or day of the death), not the date of notification, which is much more advisable to better reproduce the pandemic dynamics.
Despite the benefit of reason (2) aforementioned, it is worth to point out that even with a good transparency, the lack of reagents of molecular biology tests have caused delay in the laboratory confirmation of the COVID-19 in ES/BR (see [24], [25], [2]). This naturally causes updates of the numbers of previous days. Therefore, prior fitting the proposed model, in order to correct for delayed notifications, we extent the method in [3] by considering week days and days off and dropping the assumption of a delay window.
The remainder of this article is organized as follows: in Section 2, we present the methodology for correcting the notification delay and to predict the daily deaths and daily reported cases. In Section 3, we apply the methodology developed in Section 2 on COVID-19 dataset from Espírito Santo/Brazil. Finally, we make some concluding remarks in Section 4. The method proposed in this paper is implemented in R [23]. All codes are available with the authors upon request.
2. Methodology
2.1. Correcting notification delay
We are interested on the counts of some event at the time t, denoted by . In particular, we will apply the method in this section to the daily number of deaths and daily reported cases of COVID-19. These data naturally present a notification delay, so that is not truly known at time t and notifications occurred at t may be reported at instants . In this paper, inspired by the study in [3], we will describe this behavior as follows. Let be the total of occurrences at t notified until s, . We assume
| (1) |
where represents the number of occurrences regarding time t notified at time (delayed notifications). In this context, j will be referred to as the delay lag. The model in Equation (1) is particularly appealing in this case, since we do not have the whole evolution of the data, in particular, the data was provided only from T to , such that, when , it is only possible to obtain , for . For simplicity, we may write .
Here, aiming to account for possible overdispersion, we assume that the delayed notifications follow a Negative Binomial distribution with and , which will be denoted by . The mean satisfy
| (2) |
where λ denotes the overall mean, and accommodate respectively the temporal and the delay lag evolution of the notification process and allows for temporal changes in the delay lag effect. Equation (2) could be easily generalized to incorporate covariate effects. For simplicity, the parameter vector and the collection of observed notifications are represented by
and
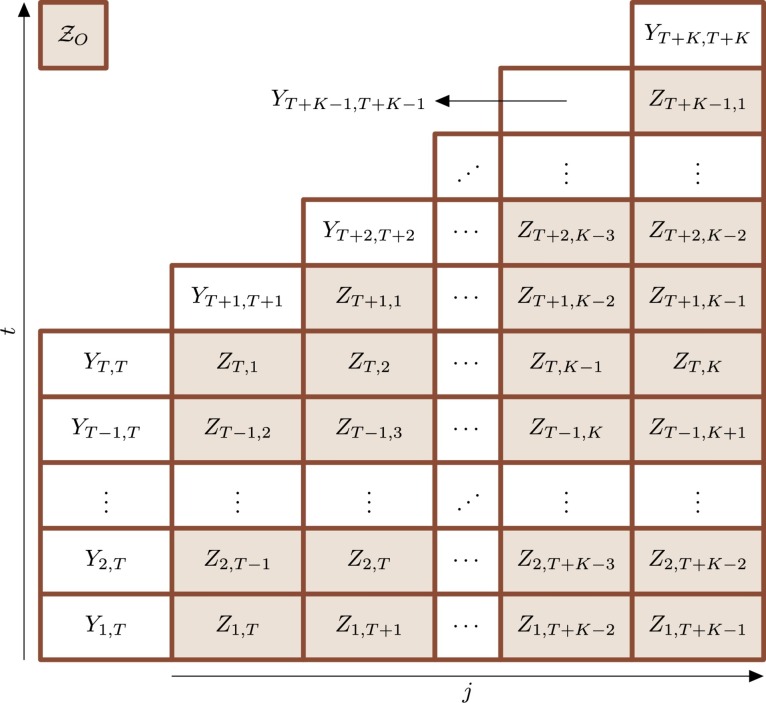
respectively. Fig. 1 shows an illustration of the data. Note that the set , , may be rewritten as , .
Fig. 1.
Organization of delayed notification data. The Zt,j (colored rectangles) denote the number of occurrences regarding time t notified at time t + j. Note that the number of available delayed notifications reduces as t increases. The Yt,s is the total of occurrences at t reported until s, s ≥ t (see Equation (1)). For example, the total of occurrences at t updated in T + K (Yt,T+K) is given by the total of occurrences at t reported until T (Yt,T) plus the delayed notifications Zt,j, .
In order to correct the notification delay, we resort to the following Bayesian approach. Aiming to accommodate the unstable nature of , and , we assume the following evolution structure:
where and we fix the variances as to ensure the parameters do not change more than 5% with probability 0.95. Fixing a correction window , for each , from Equation (1), we observe that the (future) unobserved total may be written as function of the observed total and the unobserved delayed notifications , . More precisely, we have
For simplicity, we define the collection
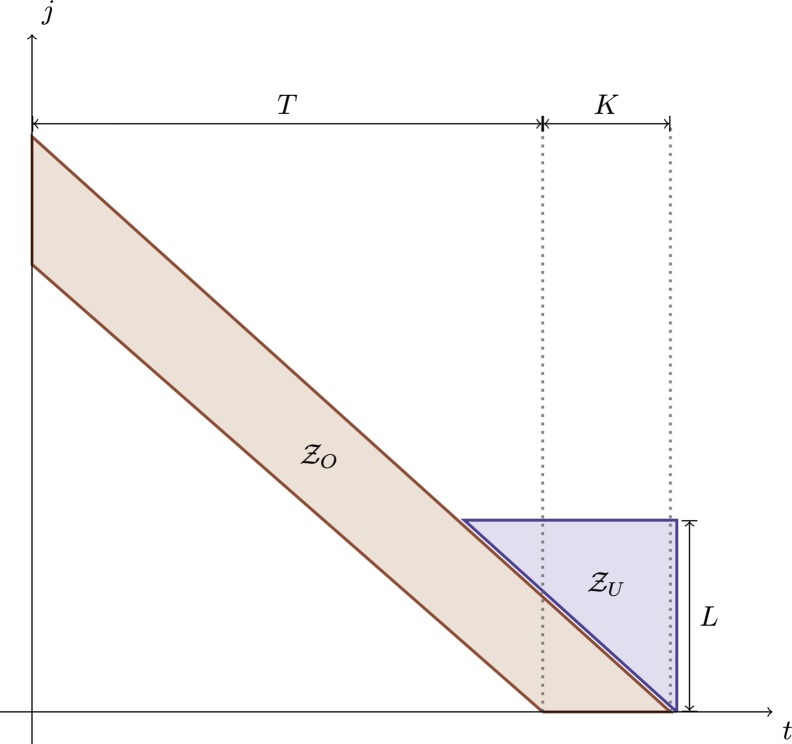
of unobserved variables. One illustration of the and collections is provided in Fig. 2 .
Fig. 2.
Observed and unobserved delayed notifications data sets represented by (red) and (blue), respectively. The unobserved set consists of the first L unobserved delayed notifications. The idea is to generate plausible observations of the unobserved set based on information of the observed set . Note that, for fixed t, the smaller the number of delayed notifications in , the greater the number of delayed notifications in . (For interpretation of the colors in the figure(s), the reader is referred to the web version of this article.)
The delay correction is implemented by drawing samples from the posterior distribution of . Assuming independence of and (conditional on Φ), this sampling can be performed using Markov Chain Monte Carlo (MCMC) methods. Here, we take as prior distributions , , , , and , where denotes the gamma distribution with expectation and variance . This means that and a priori. These values of mean and variance for ϕ express our prior belief of overdispersion for the delayed notifications in the considered data.
The delay corrected observations are
where, in this case, denote the sample mean calculated on the correspondent draws from . An illustration of the delay correction is presented in Fig. 3 .
Fig. 3.
Schematic for notification delay correction. The N = T + K denotes the more recent time. The strategy consists of generating plausible upcoming delayed notifications (up to a total of L) and synthetically update the total of occurrences (Yt,N). Note that it is necessary to generate more synthetic unobserved delayed notifications to update total of occurrences for more recent days. Specifically, we aggregate the generated to the observed total of occurrences YN−L+l,N, forming the delayed corrected total , l = 1,…,L.
2.2. Forecasting
We now discuss the methodology for daily deaths and daily reported cases prediction. For simplicity, since we will apply the method here discussed to data corrected for delayed notifications, we drop the previous notation and denote the count variable by . Once again, in order to account for possible overdispersion, we assume . We will consider a Bayesian approach to fit the model. The main step here is to choose a suitable functional form for . In this paper, inspired by [9], the starting point is to consider a generalized logistic curve to describe the expected cumulative growth denoted by . In particular, we assume
where a denotes the maximum value of , f is a skewness parameter and, when , b and c denote the inflection point and the logistic growth rate (or steepness) of , respectively. In this context, the associated functional form for is given by
| (3) |
From the pandemic point of view, the day of maximum and the maximum number of occurrences are key features. We denote these quantities by and , respectively. Rewriting (3) in terms of and will make inference and prior elicitation simpler. From (which may be obtained from ) and , we obtain these values in terms of the original parameters as
Note that, as mentioned above, when , the inflection point is . Therefore, Equation (3) may be rewritten as
| (4) |
Let denote the cumulative total of occurrences, such is . Thus, we may rewrite
| (5) |
For the daily reported cases data, a preliminary exploratory study has shown that it might be necessary to include a factor regarding week days and days off. This covariate will be denoted by . The preliminary investigation also indicates that only affects the height of , such that Equation (4) is extended to
| (6) |
where is the multiplicative effect when t refers to a day off.
Similarly to delay correction, due to the unstable nature of the phenomenon, we will assume the following dynamic evolution to parameters , and c:
where means that V follows the lognormal distribution with and and we fix the variances as to ensure the parameters do not change more than 2.5% with probability 0.95. For simplicity, the parameter vector and the collection of observed daily occurrence numbers are represented by
and
respectively. The inference was carried out by using MCMC for drawing samples from the posterior distribution of . The prior distributions for starting the evolutionary parameters were set as , and , which means that, a priori, at the beginning of the observation period we expect that, at the log scale, the day of the maximum and the daily maximum will be and , respectively. We take a bad scenario with , that is, a priori, we believe that it will take 50 more days to arise the maximum. The choice of and will be explained in Section 3. For constant parameters, we elicited the following prior distributions: ; ; and . Similarly to Subsection 2.1, this means that and a priori. Again, these values of mean and variance for θ express our prior belief of overdispersion for the daily occurrences in the considered data.
3. Application
In this section, we apply the methodology developed previously to analyze the daily deaths and the daily reported cases of COVID-19 data in Espírito Santo, Brazil. The data were obtained by systematically accessing https://coronavirus.es.gov.br/painel-covid-19-es and monitoring and recording the daily changes in the provided data.
3.1. Daily deaths
The constant parameters for the delay correction model were estimated and are presented in Table 1 . The negative values for the overall mean parameter μ indicate that the contributions to delayed notifications are mostly from the time index t and the delay lag j. Note the relatively small dispersion parameter ϕ, indicating that daily deaths notifications are moderately overdispersed.
Table 1.
Means and 0.95 HPD credibility intervals of the constant parameters.
| Measure | μ | ϕ |
|---|---|---|
| Lower | -2.0482 | 4.2033 |
| Mean | -1.6053 | 7.3644 |
| Upper | -1.1565 | 11.7102 |
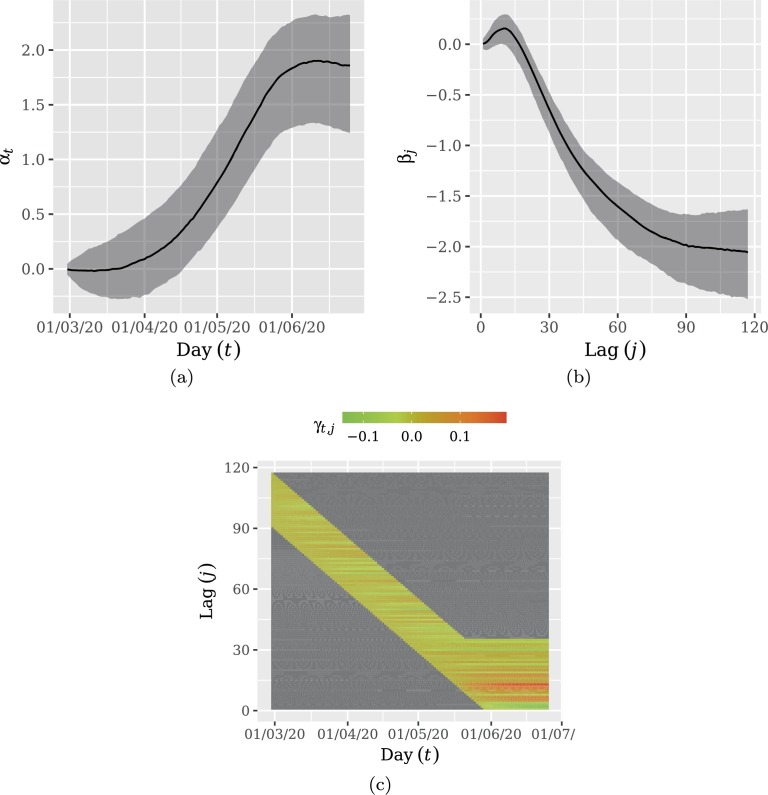
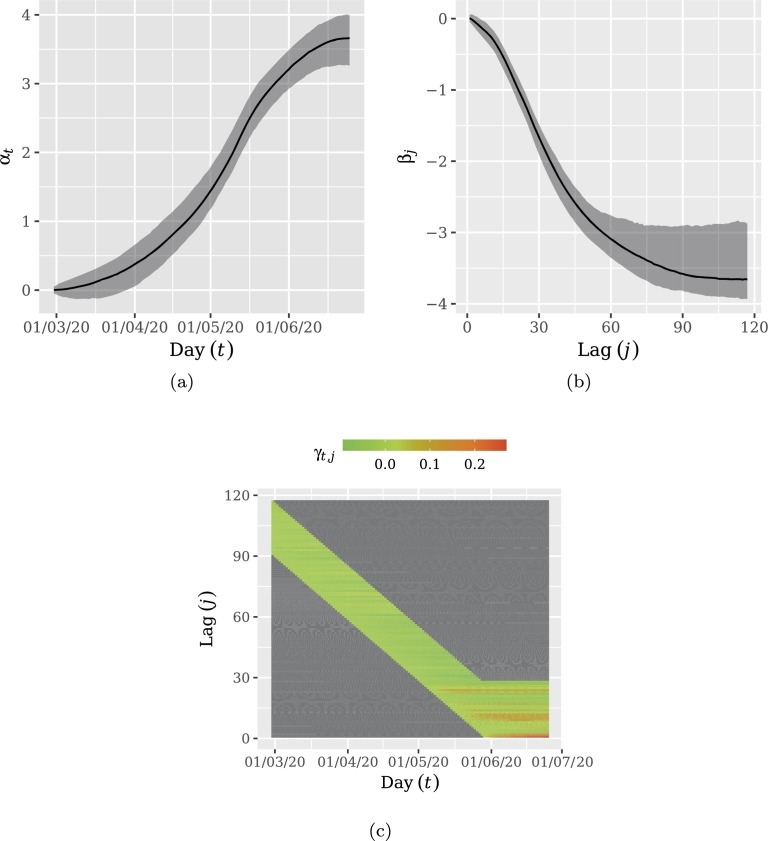
Fig. 4 display the estimated coefficients. In Figs. 4a and 4b the shaded areas represent the Highest Posterior Density (HPD) intervals with 0.95 credibility. As expected, Fig. 4a indicates that delayed notification increases with time. On the other hand, Fig. 4b shows a non-monotonous behavior, increasing for small delay lags and decreasing after a peak around a delay lag of 10 days after the corresponding day. Most delayed notifications seems to occur until 30 days after the respective day. This led us to choose the correction window as . Note the resemblance of the shapes displayed in Fig. 2, Fig. 4c. Fig. 4c indicates that delay lag increment experiences an increase for more recent days.
Fig. 4.
Coefficient evolution: (a) temporal increment, αt; (b) delay lag increment, βj; (c) temporal increment in the delay lag effect, γt,j. Shaded areas in (a) and (b) represent the Highest Posterior Density (HPD) intervals with 0.95 credibility. Frame (a) indicates that delayed notification increases with time. Frame (b) shows a non-monotonous behavior, increasing for small delay lags and decreasing after a peak around a delay lag of 10 days after the corresponding day. Frame (c) indicates that delay lag increment experiences an increase for more recent days.
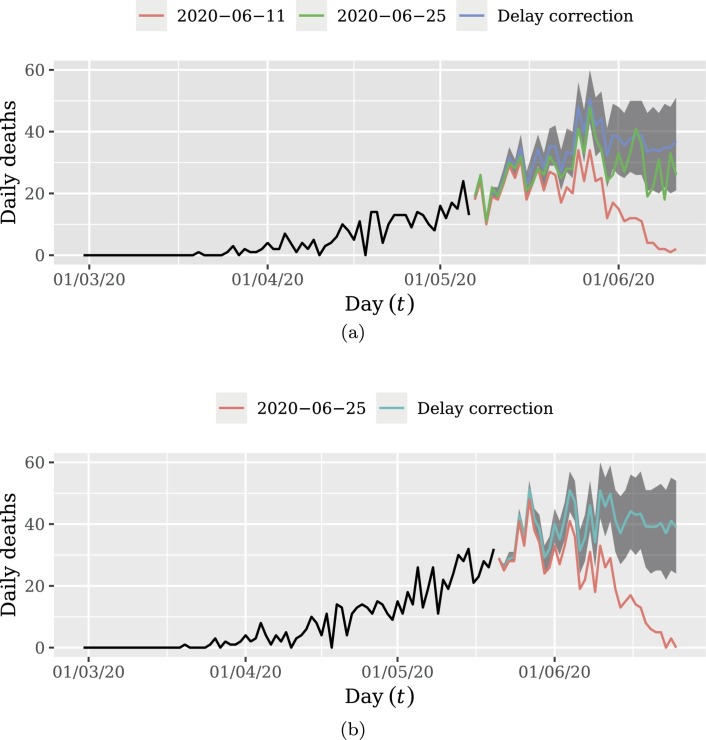
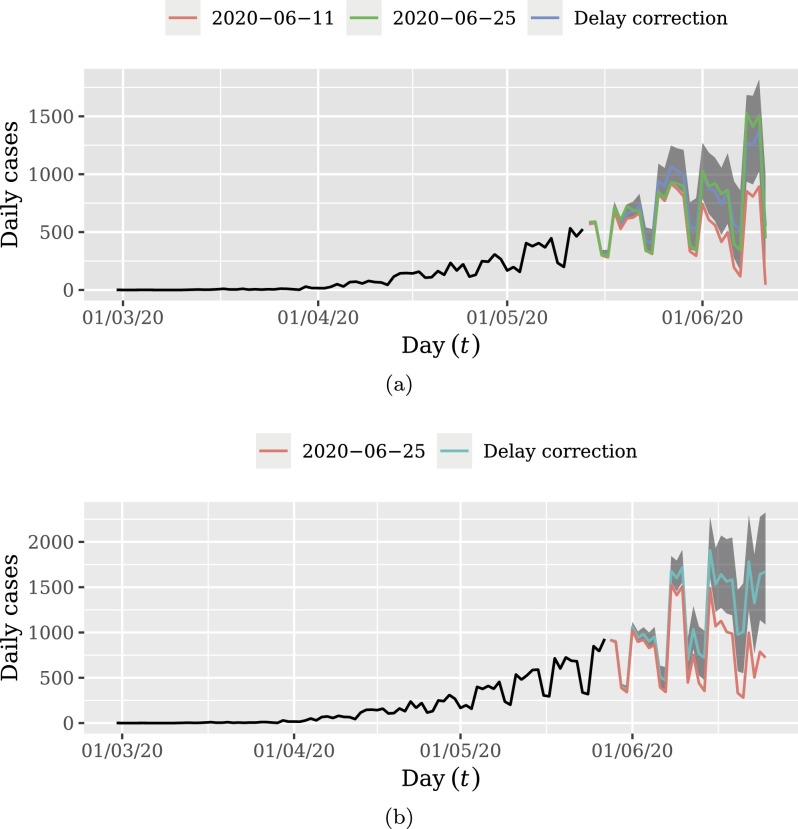
Fig. 5 shows the results of the proposed method for delay correction. Shaded areas are the 0.95 credibility intervals for delay correction. In Fig. 5a, the 14 more recent days were discarded in order to visually inspect the performance of delay correction. We note that 14 days after delay correction, the updated data tends to be inside the credibility interval. Fig. 5b presents the result of delay correction considering the whole sample, which will be used for forecasting. This plot evidences the high degree of impact caused by delayed notifications.
Fig. 5.
Delay correction of daily deaths: (a) discarding the 14 more recent days; (b) the whole data. Frame (a) shows that the methodology is able to accurately correct the total of occurrences of the period for the unobserved delayed notifications. This also evidence the high impact of disregarding future delayed notifications from the analysis. Frame (b) shows the complete delayed corrected dataset. The corrected data displayed in Frame (b) will be used to perform the forecasting.
The 14 more recent days were discarded in order to visually inspect the performance of delay correction. We note that 14 days after delay correction, the updated data tends to be inside the credibility interval. Fig. 5b presents the result of delay correction considering the whole sample, which will be used for forecasting. This plot evidences the high degree of impact caused by delayed notifications.
We now turn to investigation of the forecasting for daily deaths. We applied the methodology in Subsection 2.2 to the delay corrected daily deaths data presented in Fig. 5b. In this study, a priori, we tried to be conservative by considering bad scenarios when fitting the model. The value was taken to be around the double of the maximum observed daily deaths, which gives . In addition, considering a lethality of 4%, a underreporting percentage guess of 10%, a 50% contamination to slow down the spread of COVID-19 and the Espírito Santo state population of ≈3800000, a priori, we take the total of deaths as . Considering a symmetric behavior (), we compute the initial value using Equation (5), which gives . The estimated constant parameters are presented in Table 2 . For the ζ parameter, following [18], according to the 0.95 HPD interval, the number of daily deaths is not statistically affected by the week days and days off, since that, given the observed data, the null effect lie within the interval with the most plausible values of ζ. The estimated f indicates a right skew shape of the curve, that is the decay of the daily deaths will be slower than the growth stage.
Table 2.
Means and 0.95 HPD credibility intervals of the constant parameters.
| Measure | ζ | f | θ |
|---|---|---|---|
| Lower | -0.2925 | 1.3109 | 12.3850 |
| Mean | -0.1522 | 1.7692 | 19.8102 |
| Upper | 0.0062 | 2.3110 | 26.8390 |
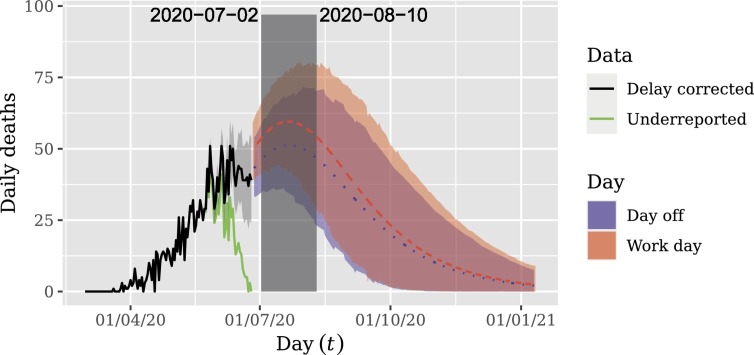
The forecast is displayed in Fig. 6 . This figure shows that the peak of daily deaths was not reached yet and will occur between July 2, 2020 and August 10, 2020 with 0.95 credibility.
Fig. 6.
Long-term forecasts for delay corrected daily deaths. Shaded areas represent 0.95 HPD forecast intervals. Note that the peak of daily deaths was not reached yet and will occur between July 2, 2020 and August 10, 2020.
3.2. Daily reported cases
The constant parameters for the delay correction model were estimated and are presented in Table 3 . Note the small dispersion parameter ϕ, indicating that daily reported cases are dramatically overdispersed.
Table 3.
Means and 0.95 HPD credibility intervals of the constant parameters.
| Measure | μ | ϕ |
|---|---|---|
| Lower | 0.0288 | 0.3490 |
| Mean | 0.3119 | 0.3877 |
| Upper | 0.6266 | 0.4300 |
Fig. 7 display the evolution of the estimated coefficients. In Figs. 7a and 7b the shaded areas represent the HPD 0.95 credibility intervals. Again, Fig. 7a indicates that delayed notification increases with time. Unlike the daily deaths data, in this case, delayed notifications present a monotonous decreasing behavior in function of delay lag (Fig. 7b). Similarly to daily deaths, most delayed notifications seem to occur until 30 days after the corresponding day. This led us to choose the correction window as . Note the resemblance of the shapes displayed in Fig. 2, Fig. 7c. Fig. 7c indicates that delay lag increment experiences an increase for more recent days.
Fig. 7.
Coefficient evolution: (a) temporal increment, αt; (b) delay lag increment, βj; (c) temporal increment in the delay lag effect, γt,j. Shaded areas in (a) and (b) represent the Highest Posterior Density (HPD) intervals with 0.95 credibility. Frame (a) indicates that delayed notification increases with time. Frame (b) shows a monotonous decreasing behavior of the delay lag increment, that is, the greater the lag the smaller the increment in the delayed notifications mean. Frame (c) indicates that delay lag increment experiences an increase for more recent days.
Fig. 8 presents the results of the proposed method for delay correction. Shaded areas are the HPD 0.95 credibility intervals for delay correction. In Fig. 8a, the 14 more recent days were discarded in order to visually inspect the performance of delay correction. We note that 14 days after delay correction, the updated data tend to be inside the credibility interval. Fig. 8b presents the result of delay correction considering the whole sample, which will be used for forecasting. This plot illustrates the major impact caused by delayed notifications.
Fig. 8.
Delay correction of daily reported cases: (a) discarding the 14 more recent days; (b) the whole data. Frame (a) shows that the methodology is able to accurately correct the total of occurrences of the period for the unobserved delayed notifications. This also evidence the high impact of disregarding future delayed notifications from the analysis. Frame (b) shows the complete delayed corrected dataset. The corrected data displayed in Frame (b) will be used to perform the forecasting.
We now turn to investigation of the forecasting for daily reported cases. The methodology of Subsection 2.2 was applied to the corrected data in Fig. 8b. For the daily reported cases, we use similar arguments to specify the initial values. The value was taken to be around the double of the maximum observed daily reported cases, which gives . In addition, considering a underreporting percentage guess of 10%, a 50% contamination to slow down the spread of COVID-19 and the Espírito Santo state population of ≈3800000, a priori, we take the total of reported cases as . Considering a symmetric behavior (), we compute the initial value using Equation (5), which gives . The estimated constant parameters are presented in Table 4 . At a 0.95 credibility level, the HPD interval for the ζ parameter shows a strong evidence to support a negative effect of day offs in reported cases. The estimated f indicates a right skewed curve, that is the decay of the daily reported cases will be slower than the growth stage.
Table 4.
Means and 0.95 HPD credibility intervals of the constant parameters.
| Measure | ζ | f | θ |
|---|---|---|---|
| Lower | -0.7429 | 1.1358 | 16.2158 |
| Mean | -0.6388 | 1.3019 | 24.2250 |
| Upper | -0.5306 | 1.5000 | 31.7097 |
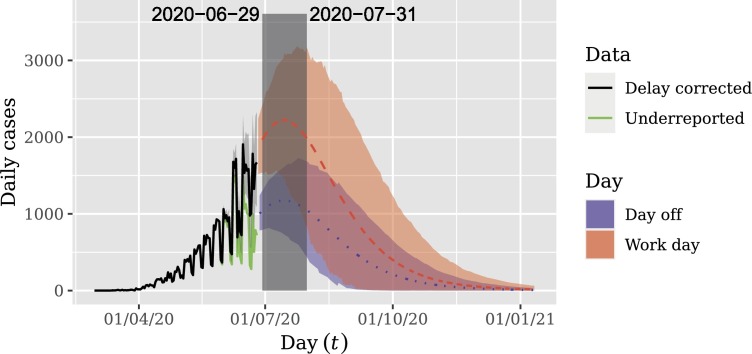
The forecast is displayed in Fig. 9 . This figure shows that the peak of daily deaths was not reached yet and will occur between June 29, 2020 and July 31, 2020 with 0.95 credibility.
Fig. 9.
Long-term forecasts for delay corrected daily reported cases. Shaded areas represent 0.95 HPD forecast intervals. Note that the peak of daily reported cases was not reached yet and will occur between June 29, 2020 and July 31, 2020.
4. Final remarks
This paper focuses in the correction of notification delay and predictions of daily COVID-19 cases and deaths. The proposed models were estimated from a Bayesian point of view. In both methods, we resorted to the negative binomial distribution in order to accommodate the overdispersion caused by the usual population heterogeneity.
The first methodology has presented good performance and has been able to capture delayed notifications. It was observed that daily death notifications are moderately overdispersed. Additionally, delayed notifications increase with time. The model was also able to show the high impact caused by delayed notifications. Another interesting result was the finding of the skewness of the curve, that is, the decay of the daily deaths will be slower than the growth stage.
The functional form and the inclusion of an explanatory variable regarding week days and days off, adopted for the prediction method, was able to explain satisfactorily the data dynamics and to provide posterior inference for maximum number of occurrences and for the peak of the occurrences. The model showed that the reported cases are highly overdispersed. Unlike the daily deaths, delayed notifications show a monotonous decreasing behavior in function of the delay lag. At last, there was strong evidence on the effect of the day in reported cases.
Although the results in this paper indicate that the proposed methods are promising, we envision as potential way of improving the results to consider the impact of media in COVID-19 dynamics. This impact has recently been considered by [17] and it would be interesting to extend our model in a similar manner.
Submitted by S.G. Krantz
References
- 1.Adamu H.A., Muhammad M., Jingi A.M., Usman M.A. Mathematical modelling using improved SIR model with more realistic assumptions. Int. J. Eng. Appl. Sci. 2019;6(1):64–69. [Google Scholar]
- 2.Avilez L. Coronavírus no ES: pacientes relatam longa espera por resultado de teste. A Gazeta. 2020 https://www.agazeta.com.br/es/cotidiano/coronavirus-no-es-pacientes-relatam-longa-espera-por-resultado-de-teste-0620 Vitória (ES/BR), accessed in April 11, 2020. [Google Scholar]
- 3.Bastos L.S., Economou T., Gomes M.F., Villela D.A., Coelho F.C., Cruz O.G., Stoner O., Bailey T., Codeço C.T. A modelling approach for correcting reporting delays in disease surveillance data. Stat. Med. 2019;38(22):4363–4377. doi: 10.1002/sim.8303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Biswas M.H.A., Paiva L.T., d M., de Pinho R. A SEIR model for control of infectious diseases with constraints. Math. Biosci. Eng. 2014;11(4):761–784. [Google Scholar]
- 5.Borges P., Godoi L.G. Pǿlya–Aeppli regression model for overdispersed count data. Stat. Model. 2019;19(4):362–385. [Google Scholar]
- 6.Brauer F. In: Mathematical Epidemiology. Brauer F., van den Driessche P., Wu J., editors. Springer Berlin Heidelberg; 2008. Compartmental models in epidemiology; pp. 19–79. [Google Scholar]
- 7.Britton T., Ball F., Trapman P. A mathematical model reveals the influence of population heterogeneity on herd immunity to SARS-CoV-2. Science. 2020;369(6505):846–849. doi: 10.1126/science.abc6810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen D. In: Analyzing and Modeling Spatial and Temporal Dynamics of Infectious Diseases. Chen D., Moulin B., Wu J., editors. John Wiley & Sons; 2014. Modeling the spread of infectious diseases: a review; pp. 19–42. [Google Scholar]
- 9.CovidLPTeam . Statistics Department, Federal University of Minas Gerais; Brazil: 2020. CovidLP: short and long term prediction for COVID-19.http://est.ufmg.br/covidlp/home/en/ Tech. Rep. accessed in June 06, 2020. [Google Scholar]
- 10.Fang Y., Nie Y., Penny M. Transmission dynamics of the COVID-19 outbreak and effectiveness of government interventions: a data-driven analysis. J. Med. Virol. 2020;92(6):645–659. doi: 10.1002/jmv.25750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Giordano G., Blanchini F., Bruno R., Colaneri P., Di Filippo A., Di Matteo A., Colaneri M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020;26:855–860. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Grant A. Dynamics of COVID-19 epidemics: SEIR models underestimate peak infection rates and overestimate epidemic duration. 2020. https://doi.org/10.1101/2020.04.02.20050674 medRxiv.
- 13.Helbing D., Brockmann D., Chadefaux T., Donnay K., Blanke U., Woolley-Meza O., Moussaid M., Johansson A., Krause J., Schutte S., et al. Saving human lives: what complexity science and information systems can contribute. J. Stat. Phys. 2015;158(3):735–781. doi: 10.1007/s10955-014-1024-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hinde J., Demétrio C.G., et al. Overdispersion: models and estimation. Comput. Stat. Data Anal. 1998;27(2):151–170. [Google Scholar]
- 15.Khajanchi S., Sarkar K. Forecasting the daily and cumulative number of cases for the COVID-19 pandemic in India, chaos: an interdisciplinary. J. Nonlinear Sci. 2020;30(7) doi: 10.1063/5.0016240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Khajanchi S., Bera S., Roy T.K. Mathematical analysis of the global dynamics of a HTLV-I infection model, considering the role of cytotoxic T-lymphocytes. Math. Comput. Simul. 2021;180:354–378. [Google Scholar]
- 17.Khajanchi S., Sarkar K., Mondal J. Dynamics of the COVID-19 pandemic in India. 2021. arXiv:2005.06286
- 18.Lindley D.V. Cambridge University Press; 1965. Introduction to Probability and Statistics from a Bayesian Viewpoint (Part 2) [Google Scholar]
- 19.Moradian N., Ochs H.D., Sedikies C., Hamblin M.R., Camargo C.A., Martinez J.A., Biamonte J.D., Abdollahi M., Torres P.J., Nieto J.J., et al. The urgent need for integrated science to fight COVID-19 pandemic and beyond. J. Transl. Med. 2020;18(1):1–7. doi: 10.1186/s12967-020-02364-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Panda S.K. Applying fixed point methods and fractional operators in the modelling of novel coronavirus 2019-nCoV/SARS-CoV-2. Results Phys. 2020;19 doi: 10.1016/j.rinp.2020.103433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Paterson R.W., Brown R.L., Benjamin L., Nortley R., Wiethoff S., Bharucha T., Jayaseelan D.L., Kumar G., Raftopoulos R.E., Zambreanu L., et al. The emerging spectrum of COVID-19 neurology: clinical, radiological and laboratory findings. Brain. 2020;143(10):3104–3120. doi: 10.1093/brain/awaa240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Perc M., Gorišek Miksić N., Slavinec M., Stožer A. Forecasting COVID-19. Front. Phys. 2020;8:127. [Google Scholar]
- 23.R Core Team . R Foundation for Statistical Computing; Vienna, Austria: 2020. R: A Language and Environment for Statistical Computing.https://www.R-project.org/ [Google Scholar]
- 24.Redação Folha Vitória Com falta de insumos para exame de COVID-19 no ES, 3 mil amostras são encaminhadas para o Paraná. Folha Vitória. 2020 https://www.folhavitoria.com.br/geral/noticia/05/2020/com-falta-de-insumos-para-exame-de-covid-19-no-es-3-mil-amostras-sao-encaminhadas-para-o-parana Vitória (ES/BR), accessed in April 30, 2020. [Google Scholar]
- 25.Redação Folha Vitória Coronavírus: com atraso na entrega de resultados, capixabas sofrem sem saber quadro clínico. Folha Vitória. 2020 https://www.folhavitoria.com.br/geral/noticia/06/2020/coronavirus-com-atraso-na-entrega-de-resultados-capixabas-sofrem-sem-saber-quadro-clinico Vitória (ES/BR), accessed in June 02, 2020. [Google Scholar]
- 26.Samui P., Mondal J., Khajanchi S. A mathematical model for COVID-19 transmission dynamics with a case study of India. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sanche S., Lin Y., Xu C., Romero-Severson E., Hengartner N., Ke R. High contagiousness and rapid spread of severe acute respiratory syndrome coronavirus 2. Emerg. Infect. Dis. 2020;26(7):1470–1477. doi: 10.3201/eid2607.200282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sarkar K., Khajanchi S., Nieto J.J. Modeling and forecasting the COVID-19 pandemic in India. Chaos Solitons Fractals. 2020;139 doi: 10.1016/j.chaos.2020.110049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schumacher F.L., Ferreira C.S., Prates M.O., Lachos A., Lachos V.H. A robust nonlinear mixed-effects model for COVID-19 deaths data. Stat. Interface. 2021;14(1):49–57. [Google Scholar]
- 30.Whitworth J. COVID-19: a fast evolving pandemic. Trans. R. Soc. Trop. Med. Hyg. 2020;114(4):241–248. doi: 10.1093/trstmh/traa025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395(10225):689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]