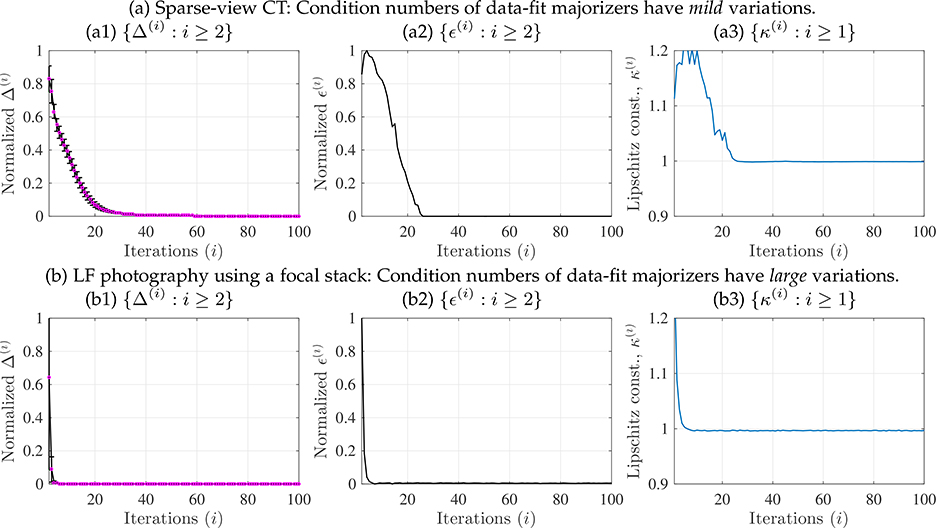
Fig. 3.

Empirical measures related to Assumption 4 for guaranteeing convergence of Momentum-Net using dCNNs refiners (for details, see (19) and §4.2.1), in different applications. See estimation procedures in §A.2. (a) The sparse-view CT reconstruction experiment used fan-beam geometry with 12.5% projections views. (b) The LF photography experiment used five detectors and reconstructed LFs consisting of 9×9 sub-aperture images. (a1, b1) For both the applications, we observed that Δ⁽ⁱ⁾ → 0. This implies that the z⁽ⁱ⁺¹⁾-updates in (Alg.1.1) satisfy the asymptotic block-coordinate minimizer condition in Assumption 4. (Magenta dots denote the mean values and black vertical error bars denote standard deviations.) (a2) Momentum-Net trained from training data-fits, where their majorization matrices have mild condition number variations, shows that ϵ⁽ⁱ⁾ → 0. This implies that paired NNs $({\mathcal{R}}_{{\theta }^{(i+1)}},{\mathcal{R}}_{{\theta }^{(i)}})$ in (Alg.1.1) are asymptotically nonexpansive. (b2) Momentum-Net trained from training training data-fits, where their majorization matrices have mild condition number variations, shows that ϵ⁽ⁱ⁾ becomes close to zero, but does not converge to zero in one hundred iterations. (a3, b3) The NNs, ${\mathcal{R}}_{{\theta }^{(i+1)}}$ in (Alg.1.1), become nonexpansive, i.e., its Lipschitz constant κ⁽ⁱ⁾ becomes less than 1, as i increases.