Short-term predictions and prevention strategies for COVID-19: A model-based study

Abstract

An outbreak of respiratory disease caused by a novel coronavirus is ongoing from December 2019. As of December 14, 2020, it has caused an epidemic outbreak with more than 73 million confirmed infections and above 1.5 million reported deaths worldwide. During this period of an epidemic when human-to-human transmission is established and reported cases of coronavirus disease 2019 (COVID-19) are rising worldwide, investigation of control strategies and forecasting are necessary for health care planning. In this study, we propose and analyze a compartmental epidemic model of COVID-19 to predict and control the outbreak. The basic reproduction number and the control reproduction number are calculated analytically. A detailed stability analysis of the model is performed to observe the dynamics of the system. We calibrated the proposed model to fit daily data from the United Kingdom (UK) where the situation is still alarming. Our findings suggest that independent self-sustaining human-to-human spread ($R_0>1,$$R_c>1$) is already present. Short-term predictions show that the decreasing trend of new COVID-19 cases is well captured by the model. Further, we found that effective management of quarantined individuals is more effective than management of isolated individuals to reduce the disease burden. Thus, if limited resources are available, then investing on the quarantined individuals will be more fruitful in terms of reduction of cases.

1. Introduction

In December 2019, an outbreak of coronavirus disease (COVID-19), was first noted in Wuhan, Central China [1]. The outbreak was declared a public health emergency of international concern on 30 January 2020 by WHO. Coronaviruses belong to the Coronaviridae family and widely distributed in humans and other mammals [31]. The virus is responsible for a range of symptoms including dry cough, fever, fatigue, breathing difficulty, and bilateral lung infiltration in severe cases, similar to those caused by Severe Acute Respiratory Syndrome Coronavirus (SARS-CoV) and Middle East Respiratory Syndrome Coronavirus (MERS-CoV) infections [27], [31]. Many people may experience non-breathing symptoms including nausea, vomiting and diarrhea [3]. Some patients have reported radiographic changes in their ground-glass lungs; normal or lower than average white blood cell lymphocyte, and platelet counts; hypoxaemia; and deranged liver and renal function. Most of them were said to be geographically connected to the Huanan seafood wholesale market, which was subsequently claimed by journalists to be selling freshly slaughtered game animals [2]. The Chinese health authority said the patients initially tested negative for common respiratory viruses and bacteria but subsequently tested positive for a novel coronavirus [16]. The SARS-CoV-2 virus spreads from person to person as confirmed in [16]. It has become an epidemic outbreak with more than 73 million confirmed infections and above 1.5 million deaths worldwide as of 14 December 2020. The current epidemic outbreak result in 1,869,666 confirmed cases and 64,402 deaths in the UK [4].

Since the first discovery and identification of coronavirus in 1965, three major outbreaks occurred, caused by emerging, highly pathogenic coronaviruses, namely the 2003 outbreak of SARS-CoV in mainland China [28], [39], the 2012 outbreak of MERS-CoV in Saudi Arabia [23], [49], and the 2015 outbreak of MERS-CoV in South Korea [21], [34]. These outbreaks resulted in SARS-CoV and MERS-CoV cases confirmed by more than 8000 and 2200, respectively [37]. The COVID-19 is caused by a new genetically similar coronavirus to the viruses that cause SARS-CoV and MERS-CoV. Despite a relatively lower death rate compared to SARS-CoV and MERS-CoV, the COVID-19 spreads rapidly and infects more people than the SARS-CoV and MERS-CoV outbreaks. In spite of strict intervention measures implemented in the region where the infection originated, the infection spread locally in Wuhan, in China and around globally.

On 31 January 2020, the UK reported the first confirmed case of acute respiratory infection due to coronavirus disease 2019 (COVID-19) and initially responded to the spread of infection by quarantining at-risk individuals. As of 14 December 2020, there were 1,869,666 confirmed cases and 64,402 confirmed deaths [4]. Within the hospitals, the infection rate is higher than in the population. On March 23, the UK government implemented a lock-down and declared that everyone should start social distancing immediately, suggesting that contact with others will be avoided as far as possible. Entire households should also quarantine themselves for 14 days if anyone has a symptom of COVID-19, and anyone at high risk of serious illness should isolate themselves for 12 weeks, including pregnant women, people over 70 and those with other health conditions. The country is literally at a standstill and the disease has seriously impacted the economy and the livelihood of the people.

As the COVID-19 is expanding rapidly in UK, real-time analyzes of epidemiological data are required to increase situational awareness and inform interventions. Earlier, in the first few weeks of an outbreak, real-time analysis shed light on the severity, transmissibility, and natural history of an emerging pathogen, such as SARS-CoV, the 2009 influenza pandemic, and Ebola [18], [19], [26], [40]. Analysis of detailed patient line lists is especially useful for inferring key epidemiological parameters, such as infectious and incubation periods, and delays between infection and detection, isolation and case reporting [18], [19]. However, official patient’s health data seldom become available to the public early in an outbreak, when the information is most required. In addition to medical and biological research, theoretical studies based on either mathematical or statistical modeling may also play an important role throughout this anti-epidemic fight in understanding the epidemic character traits of the outbreak, in predicting the inflection point and end time, and in having to decide on the measures to reduce the spread. To this end, many efforts have been made at the early stage to estimate key epidemic parameters and forecast future cases in which the statistical models are mostly used [15], [38], [44]. An Imperial College London study group calculated that 4000 (95% CI: 1000–9700) cases had occurred in Wuhan with symptoms beginning on January 18, 2020, and an estimated basic reproduction number was 2.6 (95% CI: 1.5-3.5) using the number of cases transported from Wuhan to other countries [32]. Leung et al. reached a similar finding, calculating the number of cases transported from Wuhan to other major cities in China [6] and also suggesting the possibility for the spreading of risk [11] for travel-related diseases. Mathematical modeling based on dynamic equations [7], [12], [36], [45], [46], [50], [51] may provide detailed mechanism for the disease dynamics. However, several studies were based on the UK COVID-19 situation [20], [22], [33], [35]. Davies et. al [22] studied the potential impact of different control measures for mitigating the burden of COVID-19 in the UK. They used a stochastic age-structured transmission model to explore a range of intervention scenarios. These studies have broadly suggested that control measures could reduce the burden of COVID-19. However, there is a scope of comparing popular intervention strategies namely, quarantine and isolation utilizing recent epidemic data from the UK.

In this study, we aim to study the control strategies that can significantly reduce the outbreak using a mathematical modeling framework. By mathematical analysis of the proposed model, we would like to explore transmission dynamics of the virus among humans. Another goal is the short-term prediction of new COVID-19 cases in the UK.

2. Model formulation

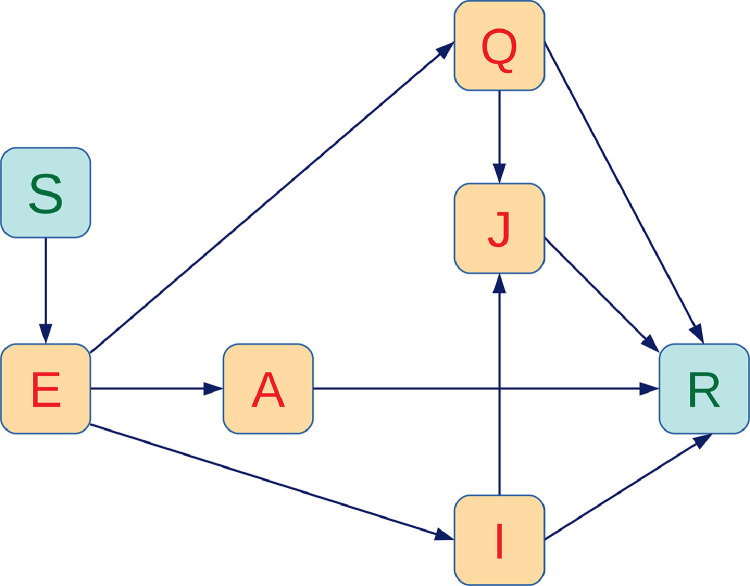
General mathematical models for the spread of infectious diseases have been described previously [25], [30], [41]. The well-known SEIR (Susceptible-Exposed-Infectious-Recovered) model has been developed by Wu et al. [55] to explain the transmission dynamics and to estimate the national and global spread of COVID-19, based on recorded data from 31 December 2019 to 28 January 2020. According to their study, the basic reproductive number for COVID-19 was found to be around 2.68. Read et al. [47] registered a value of 3.1 for the basic reproduction number based on the SEIR model, using an approximation of Poisson-distributed daily time increments. A sequence of SEIR models was designed and developed by Chen et al. [17] to explain the mechanisms of its transmission from the source of infection, reservoir, hosts to humans, since the mathematical model can draw known and definite conclusions about the outbreak of COVID-19. A generalised time-varying SEIR disease model subject to delays, which may include mixed regular and impulsive vaccination laws, was discussed in [24]. L.H.A. Monteiro investigates a SAIR epidemic model of COVID-19, which specifically takes into account four pathways of person-to-person transmission involving asymptomatic and symptomatic individuals [42]. This study shows an oscillatory convergence to the endemic steady-state, which suggests the presence of a sequence of peaks as time passes in the number of infected people. In another study, L.H.A. Monteiro et al. proposed and simulated a SAIR epidemic model based on PCA for the spread of COVID-19 [43]. This research discussed the long-term behavior of this contagious infection and, unfortunately, its transitory phase is still going on. However, we have proposed a new SEIR model for COVID-19 in the current manuscript. Two distinct classes namely, quarantine and isolation individuals are newly incorporated in the general SEAIR (Susceptible-Exposed-Asymptomatic-Infectious-Recovered) model. Here we emphasize that after successful contact, four classes of quarantine, asymptomatic, symptomatic and isolated hospitalised populations can spread the diseases to susceptible people at different intensity. Therefore, the model monitors the dynamics of seven sub-populations, namely susceptible $\left(S\right(t\left)\right),$ exposed $\left(E\right(t\left)\right),$ quarantined $\left(Q\right(t\left)\right),$ asymptomatic $\left(A\right(t\left)\right),$ symptomatic $\left(I\right(t\left)\right),$ isolated $\left(J\right(t\left)\right)$ and recovered $\left(R\right(t\left)\right)$ individuals. The total population size is $N\left(t\right)=S\left(t\right)+E\left(t\right)+Q\left(t\right)+A\left(t\right)+I\left(t\right)+J\left(t\right)+R\left(t\right)$. In this model, quarantine refers to the separation of COVID-19 infected individuals from the general population when the populations are infected but not infectious, whereas isolation describes the separation of COVID-19 infected individuals when the populations become symptomatic infectious. Our model incorporates some demographic effects by assuming a proportional natural death rate $\mu >0$ in each of the seven sub-populations of the model. In addition, our model includes a net inflow of susceptible individuals into the region at a rate $\Pi$ per unit time. This parameter includes new births, immigration and emigration. The flow diagram of the proposed model is displayed in Fig. 1 .

Fig. 1.

Compartmental flow diagram of the proposed model.

Susceptible population (S(t)):

By recruiting individuals into the region, the susceptible population is increased and reduced by natural death. Also, the susceptible population decreases after infection, acquired through interaction between a susceptible individual and an infected person who may be quarantined, asymptomatic, symptomatic, or isolated. For these four groups of infected individuals, the transmission coefficients are $\beta ,$ $r_Q\beta ,$ $r_A\beta ,$ and $r_J\beta$ respectively. We consider the $\beta$ as a transmission rate along with the modification factors for quarantined $r_Q,$ asymptomatic $r_A$ and isolated $r_J$ individuals. The interaction between infected individuals (quarantined, asymptomatic, symptomatic or isolated) and susceptible is modeled in the form of total population without quarantined and isolated individuals using standard mixing incidence [25], [30], [41]. The rate of change of the susceptible population can be expressed by the following equation:

$${\displaystyle \frac{dS}{dt}}=\Pi -\frac{S(\beta I+r_Q\beta Q+r_A\beta A+r_J\beta J)}{N}-\mu S,$$ (2.1)

Exposed population(E(t)):

Population who are exposed are infected individuals but not infectious for the community. The exposed population decreases with quarantine at a rate of ${\gamma }_1,$ and become asymptomatic and symptomatic at a rate $k_1$ and natural death at a rate $\mu$. Hence,

$${\displaystyle \frac{dE}{dt}}=\frac{S(\beta I+r_Q\beta Q+r_A\beta A+r_J\beta J)}{N}-({\gamma }_1+k_1+\mu )E$$ (2.2)

Quarantine population (Q(t)):

These are exposed individuals who are quarantined at a rate ${\gamma }_1$. For convenience, we consider that all quarantined individuals are exposed who will begin to develop symptoms and then transfer to the isolated class. Assuming that acertain portion ofuninfected individuals are also quarantined would be more plausible, but this would drastically complicate the model and require the introduction of many parameters and compartments. In addition, the error caused by our simplification is to leave certain people in the susceptible population who are currently in quarantine and therefore make less contacts. The population is reduced by the growth of clinical symptoms at a rate of $k_2$ and transferred to the isolated class. ${\sigma }_1$ is the recovery rate of quarantine individuals and $\mu$ is the natural death rate of the human population. Thus,

$${\displaystyle \frac{dQ}{dt}}={\gamma }_{1}E-(k_2+{\sigma }_1+\mu )Q$$ (2.3)

Asymptomatic population(A(t)):

Asymptomatic individuals were exposed to the virus but clinical signs of COVID have not yet developed. The exposed individuals become asymptomatic at a rate $k_1$ by a proportion $p$. The recovery rate of asymptomatic individuals is ${\sigma }_2$ and the natural death rate is $\mu$. Thus,

$${\displaystyle \frac{dA}{dt}}=p{k}_{1}E-({\sigma }_2+\mu )A$$ (2.4)

Symptomatic population(I(t)):

The symptomatic individuals are produced by a proportion of $(1-p)$ of exposed class after the exposer of clinical symptoms of COVID by exposed individuals. ${\gamma }_2$ is the isolation rate of the symptomatic individuals, ${\sigma }_3$ is the recovery rate and natural death at a rate $\mu$. Thus,

$${\displaystyle \frac{dI}{dt}}=(1-p)k_{1}E-({\gamma }_2+{\sigma }_3+\mu )I$$ (2.5)

Isolated population(J(t)):

The isolated individuals are those who have been developed by clinical symptoms and been isolated at the hospital. The isolated individuals have come from quarantined communities at a rate $k_2$ and symptomatic group at a rate ${\gamma }_2$. The recovery rate of isolated individuals is ${\sigma }_4,$ disease induced death rate is $\delta$ and natural death rate is $\mu$. Thus,

$${\displaystyle \frac{dJ}{dt}}=k_{2}Q+{\gamma }_{2}I-(\delta +{\sigma }_4+\mu )J$$ (2.6)

Recovered population(R(t)):

Quarantined, asymptomatic, symptomatic and isolated individuals recover from the disease at rates ${\sigma }_1,$ ${\sigma }_2,$ ${\sigma }_3$ and ${\sigma }_4$; respectively, and this population is reduced by a natural death rate $\mu$. It is still unclear whether the immunity due to COVID-19 is life-long or not, and hence we do not consider immunity loss in the present study. Therefore, recovered persons will not get infected even if they contact with infectious people. Thus,

$${\displaystyle \frac{dR}{dt}}={\sigma }_{1}Q+{\sigma }_{2}A+{\sigma }_{3}I+{\sigma }_{4}J-\mu R$$ (2.7)

From the above considerations, the following system of ordinary differential equations governs the dynamics of the system:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dS}{dt}}& =& \Pi -\frac{S(\beta I+r_Q\beta Q+r_A\beta A+r_J\beta J)}{N}-\mu S,\hfill \\ \hfill {\displaystyle \frac{dE}{dt}}& =& \frac{S(\beta I+r_Q\beta Q+r_A\beta A+r_J\beta J)}{N}-({\gamma }_1+k_1+\mu )E,\hfill \\ \hfill {\displaystyle \frac{dQ}{dt}}& =& {\gamma }_{1}E-(k_2+{\sigma }_1+\mu )Q,\hfill \\ \hfill {\displaystyle \frac{dA}{dt}}& =& p{k}_{1}E-({\sigma }_2+\mu )A,\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& =& (1-p)k_{1}E-({\gamma }_2+{\sigma }_3+\mu )I,\hfill \\ \hfill {\displaystyle \frac{dJ}{dt}}& =& k_{2}Q+{\gamma }_{2}I-(\delta +{\sigma }_4+\mu )J,\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}& =& {\sigma }_{1}Q+{\sigma }_{2}A+{\sigma }_{3}I+{\sigma }_{4}J-\mu R,\hfill \end{array}$$ (2.8)

All the parameters and their biological interpretation are given in Table 1 respectively.

Table 1.

Description of parameters used in the model.

Parameters	Interpretation	Value	Reference
$\Pi$	Recruitment rate	2274	[4]
$\beta$	Transmission rate	0.8883	Estimated
$r_Q$	Modification factor for quarantined	0.3	Assumed
$r_A$	Modification factor for asymptomatic	0.45	Assumed
$r_J$	Modification factor for isolated	0.6	Assumed
${\gamma }_1$	Rate at which the exposed individuals are diminished by quarantine	0.0486	Estimated
${\gamma }_2$	Rate at which the symptomatic individuals are diminished by isolation	0.1001	Estimated
$k_1$	Rate at which exposed become infected	1/7	[1]
$k_2$	Rate at which quarantined individuals are isolated	0.4129	Estimated
$p$	Proportion of asymptomatic individuals	0.13166	[52]
${\sigma }_1$	Recovery rate from quarantined individuals	0.2553	Estimated
${\sigma }_2$	Recovery rate from asymptomatic individuals	0.9982	Estimated
${\sigma }_3$	Recovery rate from symptomatic individuals	0.46	[1]
${\sigma }_4$	Recovery rate from isolated individuals	0.4449	Estimated
$\delta$	Diseases induced mortality rate	0.0015	[4]
$\mu$	Natural death rate	0.3349 $\times$${10}^{-4}$	[5]

3. Mathematical analysis

3.1. Positivity and boundedness of the solution

This subsection is provided to prove the positivity and boundedness of solutions of the system (2.8) with initial conditions ${(S\left(0\right),E\left(0\right),Q\left(0\right),A\left(0\right),I\left(0\right),J\left(0\right),R\left(0\right))}^T\in {\mathbb{R}}_{+}^7$. We first state the following lemma.

Lemma 3.1

Suppose$\Omega \subset \mathbb{R}\times {\mathbb{C}}^n$is open,$f_i\in C(\Omega ,\mathbb{R}),i=1,2,3,\dots ,n$. If$f_i{|}_{x_i\left(t\right)=0,X_t\in {\mathbb{C}}_{+0}^n}\ge 0,$$X_t={(x_{1t},x_{2t},\dots .,x_{1n})}^T,i=1,2,3,\dots .,n,$then${\mathbb{C}}_{+0}^n\{\varphi =({\varphi }_1,\dots .,{\varphi }_n):\varphi \in \mathbb{C}([-\tau ,0],{\mathbb{R}}_{+0}^n)\}$is the invariant domain of the following equations

$$\frac{d{x}_i\left(t\right)}{dt}=f_i(t,X_t),t\ge \sigma ,i=1,2,3,\dots ,n.$$

where${\mathbb{R}}_{+0}^n=\{(x_1,\dots .x_n):x_i\ge 0,i=1,\dots .,n\}$[56].

Proposition 1

The system(2.8)is invariant in${\mathbb{R}}_{+}^7$.

Proof

By re-writing the system (2.8) we have

$$\frac{dX}{dt}=M\left(X\left(t\right)\right),X\left(0\right)=X_0\ge 0$$ (3.1)

$M\left(X\left(t\right)\right)={(M_1\left(X\right),M_2\left(X\right),\cdots ,M_7\left(X\right))}^T$

We note that

$$\begin{array}{cc}\hfill \frac{dS}{dt}{|}_{S=0}& =\Pi \ge 0,\frac{dE}{dt}{|}_{E=0}=\frac{S(\beta I+r_Q\beta Q+r_A\beta A+r_J\beta J)}{S+Q+A+I+J+R}\ge 0,\hfill \\ \hfill \frac{dQ}{dt}{|}_{Q=0}& ={\gamma }_{1}E\ge 0,\frac{dA}{dt}{{|}_{A=0}=p{k}_{1}E\ge 0,\frac{dI}{dt}|}_{I=0}=(1-p)k_{1}E\ge 0,\hfill \\ \hfill \frac{dJ}{dt}{|}_{J=0}& =k_{2}Q+{\gamma }_{2}I\ge 0,\frac{dR}{dt}{|}_{R=0}={\sigma }_{1}Q+{\sigma }_{2}A+{\sigma }_{3}I+{\sigma }_{4}J\ge 0.\hfill \end{array}$$

Then it follows from the Lemma 3.1 that ${\mathbb{R}}_{+}^7$ is an invariant set. □

Proposition 2

The system(2.8)is bounded in the region

$\Omega =\{(S,E,Q,A,I,J,R)\in {\mathbb{R}}_{+}^7|S+E+Q+A+I+J+R\le \frac{\Pi }{\mu }\}$

Proof

We observed from the system that

$$\begin{array}{cc}& \frac{dN}{dt}=\Pi -\mu N-\delta J\le \Pi -\mu N\hfill \\ & ⟹\underset{t\to \infty }{lim}supN\left(t\right)\le \frac{\Pi }{\mu }\hfill \end{array}$$

Hence the system (2.8) is bounded. □

3.2. Diseases-free equilibrium and control reproduction number

The diseases-free equilibrium can be obtained for the system (2.8) by putting $E=0,Q=0,A=0,I=0,J=0,$ which is denoted by $P_1^0=(S^0,0,0,0,0,0,R^0),$ where

$$S^0=\frac{\Pi }{\mu },R^0=0.$$

The control reproduction number, a central concept in the study of the spread of communicable diseases, is e the number of secondary infections caused by a single infective in a population consisting essentially only of susceptibles with the control measures in place (quarantined and isolated class) [53]. This dimensionless number is calculated at the DFE by next generation operator method [25], [54] and it is denoted by $R_c$.

For this, we assemble the compartments which are infected from the system (2.8) and decomposing the right hand side as $\mathcal{F}-\mathcal{V},$ where $\mathcal{F}$ is the transmission part, expressing the production of new infection, and the transition part is $\mathcal{V},$ which describe the change in state.

$$\begin{array}{cc}\hfill \mathcal{F}& =\left(\begin{array}{c}\frac{S(\beta I+r_Q\beta Q+r_A\beta A+r_J\beta J)}{N}\\ 0\\ 0\\ 0\\ 0\end{array}\right),\mathcal{V}=\left(\begin{array}{c}({\gamma }_1+k_1+\mu )E\\ -{\gamma }_{1}E+(k_2+{\sigma }_1+\mu )Q\\ -p{k}_{1}E+({\sigma }_2+\mu )A\\ -(1-p)k_{1}E+({\gamma }_2+{\sigma }_3+\mu )I\\ -k_{2}Q-{\gamma }_{2}I+(\delta +{\sigma }_4+\mu )J\end{array}\right)\hfill \end{array}$$

Now we calculate the jacobian of $\mathcal{F}$ and $\mathcal{V}$ at DFE $P_1^0$

$$\begin{array}{c}\hfill F=\frac{\partial \mathcal{F}}{\partial X}=\left(\begin{array}{ccccc}0& r_Q\beta & r_A\beta & \beta & r_J\beta \\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right),\end{array}$$

$$\begin{array}{c}\hfill V=\frac{\partial \mathcal{V}}{\partial X}=\left(\begin{array}{ccccc}{\gamma }_1+k_1+\mu & 0& 0& 0& 0\\ -{\gamma }_1& k_2+{\sigma }_1+\mu & 0& 0& 0\\ -p{k}_1& 0& {\sigma }_2+\mu & 0& 0\\ -(1-p)k_1& 0& 0& {\gamma }_2+{\sigma }_3+\mu & 0\\ 0& -k_2& 0& -{\gamma }_2& \delta +{\sigma }_4+\mu \end{array}\right).\end{array}$$

Following [29], $R_c=\rho \left(F{V}^{-1}\right),$ where $\rho$ is the spectral radius of the next-generation matrix ($F{V}^{-1}$). Thus, from the model (2.8), we have the following expression for $R_c$:

$$\begin{array}{cc}\hfill R_c& =\frac{r_Q\beta {\gamma }_1}{({\gamma }_1+k_1+\mu )(k_2+{\sigma }_1+\mu )}+\frac{r_A\beta p{k}_1}{({\gamma }_1+k_1+\mu )({\sigma }_2+\mu )}\hfill \\ \hfill & +\frac{\beta k_1(1-p)}{({\gamma }_1+k_1+\mu )({\gamma }_2+{\sigma }_3+\mu )}+\frac{r_J\beta {\gamma }_1{k}_2}{({\gamma }_1+k_1+\mu )(k_2+{\sigma }_1+\mu )(\delta +{\sigma }_4+\mu )}\hfill \\ \hfill & +\frac{r_J\beta (1-p)k_1{\gamma }_2}{({\gamma }_1+k_1+\mu )({\gamma }_2+{\sigma }_3+\mu )(\delta +{\sigma }_4+\mu )}\hfill \\ \hfill \end{array}$$ (3.2)

3.3. Stability of DFE

Theorem 3.1

The diseases free equilibrium(DFE) $P_1^0=(S^0,0,0,0,0,0,R^0)$ of the system (2.8) is locally asymptotically stable if $R_c<1$ and unstable if $R_c>1$ .

Proof

We calculate the Jacobian of the system (2.8) at DFE, and is given by

$$\begin{array}{c}\hfill J_{P_1^0}=\left(\begin{array}{ccccccc}-\mu & 0& -r_Q\beta & -r_A\beta & -\beta & -r_J\beta & 0\\ 0& -({\gamma }_1+k_1+\mu )& r_Q\beta & r_A\beta & \beta & r_J\beta & 0\\ 0& {\gamma }_1& -(k_2+{\sigma }_1+\mu )& 0& 0& 0& 0\\ 0& p{k}_1& 0& -({\sigma }_2+\mu )& 0& 0& 0\\ 0& (1-p)k_1& 0& 0& -({\gamma }_2+{\sigma }_3+\mu )& 0& 0\\ 0& 0& k_2& 0& {\gamma }_2& -(\delta +{\sigma }_4+\mu )& 0\\ 0& 0& {\sigma }_1& {\sigma }_2& {\sigma }_3& {\sigma }_4& -\mu \end{array}\right),\end{array}$$

Let $\lambda$ be the eigenvalue of the matrix $J_{P_1^0}$. Then the characteristic equation is given by $det(J_{P_1^0}-\lambda I)=0$.

$\Rightarrow$$r_J\beta {\gamma }_1{k}_2(\lambda +{\sigma }_2+\mu )(\lambda +{\gamma }_2+{\sigma }_3+\mu )+r_J\beta {\gamma }_2{k}_1(\lambda +k_2+{\sigma }_1+\mu )\left[(1-p)(\lambda +{\sigma }_2+\mu )\right]+r_A\beta p{k}_1(\lambda +{\gamma }_2+{\sigma }_3+\mu )(\lambda +\delta +{\sigma }_4+\mu )(\lambda +k_2+{\sigma }_1+\mu )+\beta k_1\left[(1-p)(\lambda +{\sigma }_2+\mu )\right](\lambda +\delta +{\sigma }_4+\mu )(\lambda +k_2+{\sigma }_1+\mu )-(\lambda +{\gamma }_1+k_1+\mu )(\lambda +{\sigma }_2+\mu )(\lambda +{\gamma }_2+{\sigma }_3+\mu )(\lambda +\delta +{\sigma }_4+\mu )(\lambda +k_2+{\sigma }_1+\mu )=0$.

Which can be written as

$$\begin{array}{cc}& \frac{r_Q\beta {\gamma }_1}{(\lambda +{\gamma }_1+k_1+\mu )(\lambda +k_2+{\sigma }_1+\mu )}+\frac{r_A\beta p{k}_1}{(\lambda +{\gamma }_1+k_1+\mu )(\lambda +{\sigma }_2+\mu )}\hfill \\ \hfill & +\frac{\beta k_1(1-p)}{(\lambda +{\gamma }_1+k_1+\mu )(\lambda +{\gamma }_2+{\sigma }_3+\mu )}\hfill \\ \hfill & +\frac{r_J\beta {\gamma }_1{k}_2}{(\lambda +{\gamma }_1+k_1+\mu )(\lambda +k_2+{\sigma }_1+\mu )(\lambda +\delta +{\sigma }_4+\mu )}\hfill \\ \hfill & +\frac{r_J\beta (1-p)k_1{\gamma }_2}{(\lambda +{\gamma }_1+k_1+\mu )(\lambda +{\gamma }_2+{\sigma }_3+\mu )(\lambda +\delta +{\sigma }_4+\mu )}=1=G_1\left(\lambda \right)\left(say\right).\hfill \end{array}$$

We rewrite $G_1\left(\lambda \right)$ as $G_1\left(\lambda \right)=G_{11}\left(\lambda \right)+G_{12}\left(\lambda \right)+G_{13}\left(\lambda \right)+G_{14}\left(\lambda \right)+G_{15}\left(\lambda \right)$

Now if $Re\left(\lambda \right)\ge 0,$ $\lambda =x+iy,$ then

$$\begin{array}{cc}\hfill |G_{11}\left(\lambda \right)|& \le \frac{r_Q\beta {\gamma }_1}{|\lambda +{\gamma }_1+k_1+\mu \parallel \lambda +k_2+{\sigma }_1+\mu |}\le G_{11}\left(x\right)\le G_{11}\left(0\right)\hfill \\ \hfill |G_{12}\left(\lambda \right)|& \le \frac{r_A\beta p{k}_1}{|\lambda +{\gamma }_1+k_1+\mu \parallel \lambda +{\sigma }_2+\mu |}\le G_{12}\left(x\right)\le G_{12}\left(0\right)\hfill \\ \hfill |G_{13}\left(\lambda \right)|& \le \frac{\beta k_1(1-p)}{|\lambda +{\gamma }_1+k_1+\mu \parallel \lambda +{\gamma }_2+{\sigma }_3+\mu |}\le G_{13}\left(x\right)\le G_{13}\left(0\right)\hfill \\ \hfill |G_{14}\left(\lambda \right)|& \le \frac{r_J\beta {\gamma }_1{k}_2}{|\lambda +{\gamma }_1+k_1+\mu \parallel \lambda +k_2+{\sigma }_1+\mu \parallel \lambda +\delta +{\sigma }_4+\mu |}\le G_{14}\left(x\right)\le G_{14}\left(0\right)\hfill \\ \hfill |G_{15}\left(\lambda \right)|& \le \frac{r_J\beta (1-p)k_1{\gamma }_2}{|\lambda +{\gamma }_1+k_1+\mu \parallel \lambda +{\gamma }_2+{\sigma }_3+\mu \parallel \lambda +\delta +{\sigma }_4+\mu |}\le G_{15}\left(x\right)\le G_{15}\left(0\right)\hfill \end{array}$$

Then $G_{11}\left(0\right)+G_{12}\left(0\right)+G_{13}\left(0\right)+G_{14}\left(0\right)+G_{15}\left(0\right)=G_1\left(0\right)=R_c<1,$ which implies $|G_1\left(\lambda \right)|\le 1$.

Thus for $R_c<1,$ all the eigenvalues of the characteristics equation $G_1\left(\lambda \right)=1$ has negative real parts.

Therefore if $R_c<1,$ all eigenvalues are negative and hence DFE $P_1^0$ is locally asymptotically stable.

Now if we consider $R_c>1$ i.e $G_1\left(0\right)>1,$ then

$$\underset{\lambda \to \infty }{lim}{G}_1\left(\lambda \right)=0.$$

Then there exist ${\lambda }_1^{*}>0$ such that $G_1\left({\lambda }_1^{*}\right)=1$.

That means there exist positive eigenvalue ${\lambda }_1^{*}>0$ of the Jacobian matrix.

Hence DFE $P_1^0$ is unstable whenever $R_c>1$. □

Theorem 3.2

The diseases free equilibrium (DFE) $P_1^0=(S^0,0,0,0,0,0,R^0)$ is globally asymptotically stable (GAS) for the system (2.8) if $R_c<1$ and unstable if $R_c>1$ .

Proof

We rewrite the system (2.8) as

$$\begin{array}{cc}\hfill \frac{dX}{dt}& =F(X,V)\hfill \\ \hfill \frac{dV}{dt}& =G(X,V),G(X,0)=0\hfill \end{array}$$

where $X=(S,R)\in R_2$ (the number of uninfected individuals compartments), $V=(E,Q,A,I,J)\in R_5$ (the number of infected individuals compartments), and $P_1^0=(\frac{\Pi }{\mu },0,0,0,0,0,0)$ is the DFE of the system (2.8). The global stability of the DFE is guaranteed if the following two conditions are satisfied:

• 1.For $\frac{dX}{dt}=F(X,0),$ $X^{*}$ is globally asymptotically stable,
• 2.$G(X,V)=BV-\widehat{G}(X,V),$$\widehat{G}(X,V)\ge 0$ for $(X,V)\in \Omega ,$

where $B=D_{V}G(X^{*},0)$ is a Metzler matrix and $\Omega$ is the positively invariant set with respect to the model (2.8). Following Castillo-Chavez et al [13], we check for aforementioned conditions. For system (2.8),

$$F(X,0)=\left(\begin{array}{c}\Pi -\mu S\\ 0\end{array}\right),$$

$$B=\left(\begin{array}{ccccc}-({\gamma }_1+k_1+\mu )& r_Q\beta & r_A\beta & \beta & r_J\beta \\ {\gamma }_1& -(k_2+{\sigma }_1+\mu )& 0& 0& 0\\ p{k}_1& 0& -({\sigma }_2+\mu )& 0& 0\\ (1-p)k_1& 0& 0& -({\gamma }_2+{\sigma }_3+\mu )& 0\\ 0& k_2& 0& {\gamma }_2& -(\delta +{\sigma }_4+\mu )\end{array}\right)$$

and

$$\begin{array}{c}\hfill \widehat{G}(X,V)=\left(\begin{array}{c}{r}_Q\beta Q(1-\frac{S}{N})+r_A\beta A(1-\frac{S}{N})+\beta I(1-\frac{S}{N})+r_J\beta J(1-\frac{S}{N})\\ 0\\ 0\\ 0\\ 0\end{array}\right).\end{array}$$

Clearly, $\widehat{G}(X,V)\ge 0$ whenever the state variables are inside $\Omega$. Also it is clear that $X^{*}=(\frac{\Pi }{\mu },0)$ is a globally asymptotically stable equilibrium of the system $\frac{dX}{dt}=F(X,0)$. Hence, the theorem follows. □

3.4. Existence and local stability of endemic equilibrium

In this section, the existence of the endemic equilibrium of the model (2.8) is established. Let us denote

$$\begin{array}{cc}\hfill m_1& ={\gamma }_1+k_1+\mu ,m_2=k_2+{\sigma }_1+\mu ,m_3={\sigma }_2+\mu ,\hfill \\ \hfill m_4& ={\gamma }_2+{\sigma }_3+\mu ,m_5=\delta +{\sigma }_4+\mu .\hfill \end{array}$$

Let $P_1^{*}=(S^{*},E^{*},Q^{*},A^{*},I^{*},J^{*},R^{*})$ represents any arbitrary endemic equilibrium point (EEP) of the model (2.8). Further, define

$${\eta }^{*}=\frac{\beta (I^{*}+r_Q{Q}^{*}+r_A{A}^{*}+r_J{J}^{*})}{N^{*}}$$ (3.3)

It follows, by solving the equations in (2.8) at steady-state, that

$$\begin{array}{cc}\hfill S^{*}& =\frac{\Pi }{{\eta }^{*}+\mu },E^{*}=\frac{{\eta }^{*}{S}^{*}}{m_1},Q^{*}=\frac{{\gamma }_1{\eta }^{*}{S}^{*}}{m_1{m}_2},A^{*}=\frac{p{k}_1{\eta }^{*}{S}^{*}}{m_1{m}_3},\hfill \\ \hfill I^{*}& =\frac{(1-p)k_1{\eta }^{*}{S}^{*}}{m_1{m}_4},J^{*}=\frac{{\eta }^{*}{S}^{*}(k_2{\gamma }_1{m}_4+(1-p)k_1{\gamma }_2{m}_2)}{m_1{m}_2{m}_4{m}_5}\hfill \\ \hfill R^{*}& =\frac{{\eta }^{*}{S}^{*}[{\sigma }_1{\gamma }_1{m}_3{m}_4{m}_5+p{k}_1{\sigma }_2{m}_2{m}_4{m}_5+(1-p)k_1{\sigma }_3{m}_2{m}_3{m}_5+m_3{\sigma }_4(k_2{\gamma }_1{m}_4+(1-p)k_1{\gamma }_2{m}_2)]}{\mu m_1{m}_2{m}_3{m}_4{m}_5}\hfill \end{array}$$ (3.4)

Substituting the expression in (3.4) into (3.3) shows that the non-zero equilibrium of the model (2.8) satisfy the following linear equation, in terms of ${\eta }^{*}$:

$$A{\eta }^{*}+B=0$$ (3.5)

where

$$\begin{array}{cc}\hfill A& =\mu [m_2{m}_3{m}_4{m}_5+{\gamma }_1{m}_3{m}_4{m}_5+p{k}_1{m}_2{m}_4{m}_5+(1-p)k_1{m}_2{m}_3{m}_5+k_2{\gamma }_1{m}_3{m}_4\hfill \\ & +(1-p)k_1{\gamma }_2{m}_2{m}_3]+{\sigma }_1{\gamma }_1{m}_3{m}_4{m}_5+{\sigma }_{2}p{k}_1{m}_2{m}_4{m}_5+(1-p)k_1{\sigma }_3{m}_2{m}_3{m}_5\hfill \\ & +{\sigma }_4{k}_2{\gamma }_1{m}_3{m}_4+(1-p){\sigma }_4{\gamma }_2{k}_1{m}_2{m}_3\hfill \\ \hfill B& =\mu m_1{m}_2{m}_3{m}_4{m}_5(1-R_c)\hfill \end{array}$$

Since $A>0,$ $\mu >0,$ $m_1>0,$ $m_2>0,$ $m_3>0,$ $m_4>0$ and $m_5>0,$ it is clear that the model (2.8) has a unique endemic equilibrium point (EEP) whenever $R_c>1$ and no positive endemic equilibrium point whenever $R_c<1$. This rules out the possibility of the existence of equilibrium other than DFE whenever $R_c<1$. Furthermore, it can be shown that, the DFE $P_1^0$ of the model (2.8) is globally asymptotically stable (GAS) whenever $R_c<1$.

From the above discussion we have concluded that

Theorem 3.3

The model(2.8)has a unique endemic (positive) equilibrium, given by$P_1^{*},$whenever$R_c>1$and has no endemic equilibrium for$R_c\le 1$.

Now we will prove the local stability of endemic equilibrium.

Theorem 3.4

The endemic equilibrium$P_1^{*}$is locally asymptotically stable if$R_C>1$.

Proof

Let $x={(x_1,x_2,x_3,x_4,x_5,x_6,x_7)}^T={(S,E,Q,A,I,J,R)}^T$. Thus, the model (2.8) can be re-written in the form $\frac{dx}{dt}=f\left(x\right),$ with $f\left(x\right)=(f_1\left(x\right),\dots .,f_7\left(x\right)),$ as follows:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{x}_1}{dt}}& =& \Pi -\frac{x_1(\beta x_5+r_Q\beta x_3+r_A\beta x_4+r_J\beta x_6)}{x_1+x_2+x_3+x_4+x_5+x_6+x_7}-\mu x_1,\hfill \\ \hfill {\displaystyle \frac{d{x}_2}{dt}}& =& \frac{x_1(\beta x_5+r_Q\beta x_3+r_A\beta x_4+r_J\beta x_6)}{x_1+x_2+x_3+x_4+x_5+x_6+x_7}-({\gamma }_1+k_1+\mu )x_2,\hfill \\ \hfill {\displaystyle \frac{d{x}_3}{dt}}& =& {\gamma }_1{x}_2-(k_2+{\sigma }_1+\mu )x_3,\hfill \\ \hfill {\displaystyle \frac{d{x}_4}{dt}}& =& p{k}_1{x}_2-({\sigma }_2+\mu )x_4,\hfill \\ \hfill {\displaystyle \frac{d{x}_5}{dt}}& =& (1-p)k_1{x}_2-({\gamma }_2+{\sigma }_3+\mu )x_5,\hfill \\ \hfill {\displaystyle \frac{d{x}_6}{dt}}& =& k_2{x}_3+{\gamma }_2{x}_5-(\delta +{\sigma }_4+\mu )x_6,\hfill \\ \hfill {\displaystyle \frac{d{x}_7}{dt}}& =& {\sigma }_1{x}_3+{\sigma }_2{x}_4+{\sigma }_3{x}_5+{\sigma }_4{x}_6-\mu x_7,\hfill \end{array}$$ (3.6)

The Jacobian matrix of the system (3.6) $J_{P_1^0}$ at DFE is given by

$$\begin{array}{c}\hfill J_{P_1^0}=\left(\begin{array}{ccccccc}-\mu & 0& -r_Q\beta & -r_A\beta & -\beta & -r_J\beta & 0\\ 0& -({\gamma }_1+k_1+\mu )& r_Q\beta & r_A\beta & \beta & r_J\beta & 0\\ 0& {\gamma }_1& -(k_2+{\sigma }_1+\mu )& 0& 0& 0& 0\\ 0& p{k}_1& 0& -({\sigma }_2+\mu )& 0& 0& 0\\ 0& (1-p)k_1& 0& 0& -({\gamma }_2+{\sigma }_3+\mu )& 0& 0\\ 0& 0& k_2& 0& {\gamma }_2& -(\delta +{\sigma }_4+\mu )& 0\\ 0& 0& {\sigma }_1& {\sigma }_2& {\sigma }_3& {\sigma }_4& -\mu \end{array}\right),\end{array}$$

Here, we use the central manifold theory method to determine the local stability of the endemic equilibrium by taking $\beta$ as bifurcation parameter [14]. Select $\beta$ as the bifurcation parameter and gives critical value of $\beta$ at $R_C=1$ is given as

$${\beta }^{*}=\frac{({\gamma }_1+k_1+\mu )(k_2+{\sigma }_1+\mu )({\sigma }_2+\mu )({\gamma }_2+{\sigma }_3+\mu )(\delta +{\sigma }_4+\mu )}{[r_Q{\gamma }_1({\sigma }_2+\mu )({\gamma }_2+{\sigma }_3+\mu )(\delta +{\sigma }_4+\mu )+r_{A}p{k}_1(k_2+{\sigma }_1+\mu )({\gamma }_2+{\sigma }_3+\mu )(\delta +{\sigma }_4+\mu )+Z]}$$

where, $Z=k_1(1-p)(k_2+{\sigma }_1+\mu )({\sigma }_2+\mu )(\delta +{\sigma }_4+\mu )+r_J{\gamma }_1{k}_2({\sigma }_2+\mu )({\gamma }_2+{\sigma }_3+\mu )+r_J(1-p)k_1{\gamma }_2(k_2+{\sigma }_1+\mu )({\sigma }_2+\mu )$

The Jacobian of (2.8) at $\beta ={\beta }^{*},$ denoted by $J_{P_1^0}{|}_{\beta ={\beta }^{*}}$ has a right eigenvector (corresponding to the zero eigenvalue) given by $w={(w_1,w_2,w_3,w_4,w_5,w_6,w_7)}^T$, where

$$\begin{array}{cc}& w_1=-\frac{{\gamma }_1+k_1+\mu }{\mu }{w}_2,w_2=w_2>0,w_3=\frac{{\gamma }_1}{k_2+{\sigma }_1+\mu }{w}_2,w_4=\frac{p{k}_1}{{\sigma }_2+\mu }{w}_2,\hfill \\ & w_5=\frac{(1-p)k_1}{{\gamma }_2+{\sigma }_3+\mu }{w}_2,w_6=\frac{k_2{\gamma }_1}{(\delta +{\sigma }_4+\mu )(k_2+{\sigma }_1+\mu )}{w}_2+\frac{{\gamma }_2(1-p)k_1}{(\delta +{\sigma }_4+\mu )({\gamma }_2+{\sigma }_3+\mu )}{w}_2\hfill \\ & w_7=\frac{1}{\mu }[\frac{{\sigma }_1{\gamma }_1}{k_2+{\sigma }_1+\mu }{w}_2+\frac{{\sigma }_{2}p{k}_1}{{\sigma }_2+\mu }{w}_2+\frac{{\sigma }_3(1-p)k_1}{{\gamma }_2+{\sigma }_3+\mu ]w_2}+\frac{{\sigma }_4{k}_2{\gamma }_1}{(\delta +\sigma +\mu )(k_2+{\sigma }_1+\mu )}{w}_2\hfill \\ & +\frac{{\sigma }_4{\gamma }_2(1-p)k_1}{(\delta +\sigma +\mu )({\gamma }_2+{\sigma }_3+\mu )}{w}_2].\hfill \end{array}$$

Similarly, from $J_{P_1^0}{|}_{\beta ={\beta }^{*}},$ we obtain a left eigenvector $v=(v_1,v_2,v_3,v_4,v_5,v_6,v_7)$ (corresponding to the zero eigenvalue), where

$$\begin{array}{cc}& v_1=0,v_2=v_2>0,v_3=\frac{r_Q{\beta }^{*}}{k_2+{\sigma }_1+\mu }{v}_2+\frac{k_2{r}_J{\beta }^{*}}{(k_2+{\sigma }_1+\mu )(\delta +{\sigma }_4+\mu )}{v}_2,v_4=\frac{r_A{\beta }^{*}}{{\sigma }_2+\mu }{v}_2,\hfill \\ & v_5=\frac{{\beta }^{*}}{{\gamma }_2+{\sigma }_3+\mu }{v}_2+\frac{{\gamma }_2{r}_J{\beta }^{*}}{({\gamma }_2+{\sigma }_3+\mu )(\delta +{\sigma }_4+\mu )}{v}_2,v_6=\frac{r_J{\beta }^{*}}{\delta +{\sigma }_4+\mu }{v}_2,v_7=0.\hfill \end{array}$$

We calculate the following second order partial derivatives of $f_i$ at the disease-free equilibrium $P_1^0$ to show the stability of the endemic equilibrium and obtain

$$\begin{array}{cc}\hfill \frac{{\partial }^2{f}_2}{\partial x_3\partial x_2}& =-\frac{\beta r_Q\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_4\partial x_2}=-\frac{\beta r_A\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_5\partial x_2}=-\frac{\beta \mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_6\partial x_2}=-\frac{\beta r_J\mu }{\Pi },\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_2\partial x_3}& =-\frac{\beta r_Q\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_3\partial x_3}=-\frac{2\beta r_Q\mu }{\pi },\frac{{\partial }^2{f}_2}{\partial x_4\partial x_3}=-\frac{\beta r_Q\mu }{\Pi }-\frac{\beta r_A\mu }{\Pi },\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_5\partial x_3}& =-\frac{\beta r_Q\mu }{\Pi }-\frac{\beta \mu }{\pi },\frac{{\partial }^2{f}_2}{\partial x_6\partial x_3}=-\frac{\beta r_Q\mu }{\pi }-\frac{\beta r_J\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_7\partial x_3}=-\frac{\beta r_Q\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_2\partial x_4}=-\frac{\beta r_A\mu }{\Pi },\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_3\partial x_4}& =-\frac{\beta r_A\mu }{\Pi }-\frac{\beta r_Q\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_4\partial x_4}=-\frac{2\beta r_A\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_5\partial x_4}=-\frac{\beta r_A\mu }{\Pi }-\frac{\beta \mu }{\Pi },\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_6\partial x_4}& =-\frac{\beta r_A\mu }{\Pi }-\frac{\beta r_J\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_7\partial x_4}=-\frac{\beta r_A\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_2\partial x_5}=-\frac{\beta \mu }{\Pi },\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_3\partial x_5}& =-\frac{\beta \mu }{\Pi }-\frac{\beta r_Q\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_4\partial x_5}=-\frac{\beta \mu }{\Pi }-\frac{\beta r_A\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_5\partial x_5}=-\frac{2\beta \mu }{\Pi },\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_6\partial x_5}& =-\frac{\beta \mu }{\pi }-\frac{\beta r_J\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_7\partial x_5}=-\frac{\beta \mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_2\partial x_6}=-\frac{\beta r_J\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_3\partial x_6}=-\frac{\beta r_J\mu }{\Pi }-\frac{\beta r_Q\mu }{\Pi },\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_4\partial x_6}& =-\frac{\beta r_J\mu }{\Pi }-\frac{\beta r_A\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_5\partial x_6}=-\frac{\beta r_J\mu }{\Pi }-\frac{\beta \mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_6\partial x_6}=-\frac{2\beta r_J\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_7\partial x_6}=-\frac{\beta r_J\mu }{\Pi },\hfill \\ \hfill \frac{{\partial }^2{f}_2}{\partial x_3\partial x_7}& =-\frac{\beta r_Q\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_4\partial x_7}=\frac{\beta r_A\mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_5\partial x_7}=-\frac{\beta \mu }{\Pi },\frac{{\partial }^2{f}_2}{\partial x_6\partial x_7}=-\frac{\beta r_J\mu }{\Pi }\hfill \end{array}$$

Now we calculate the coefficients $a$ and $b$ defined in Theorem 4.1 [14] of CastilloChavez and Song as follow

$$a=\sum _{k,i,j=1}^7{v}_k{w}_i{w}_j\frac{{\partial }^2{f}_k(0,0)}{\partial x_i\partial x_j}$$

and

$$b=\sum _{k,i=1}^7{v}_k{w}_i\frac{{\partial }^2{f}_k(0,0)}{\partial x_i\partial \beta }$$

Replacing the values of all the second-order derivatives measured at DFE and $\beta ={\beta }^{*},$ we get

$$a=-\frac{2{\beta }^{*}\mu v_2}{\Pi }(r_Q{w}_3+r_A{w}_4+w_5+r_J{w}_6)(w_2+w_3+w_4+w_5+w_6+w_7)<0$$

and

$$b=v_2(r_Q{w}_3+r_A{w}_4+w_5+r_J{w}_6)>0$$

Since $a<0$ and $b>0$ at $\beta ={\beta }^{*},$ therefore using the Remark 1 of the Theorem 4.1 stated in [14], a transcritical bifurcation occurs at $R_C=1$ and the unique endemic equilibrium is locally asymptotically stable for $R_C>1$. □

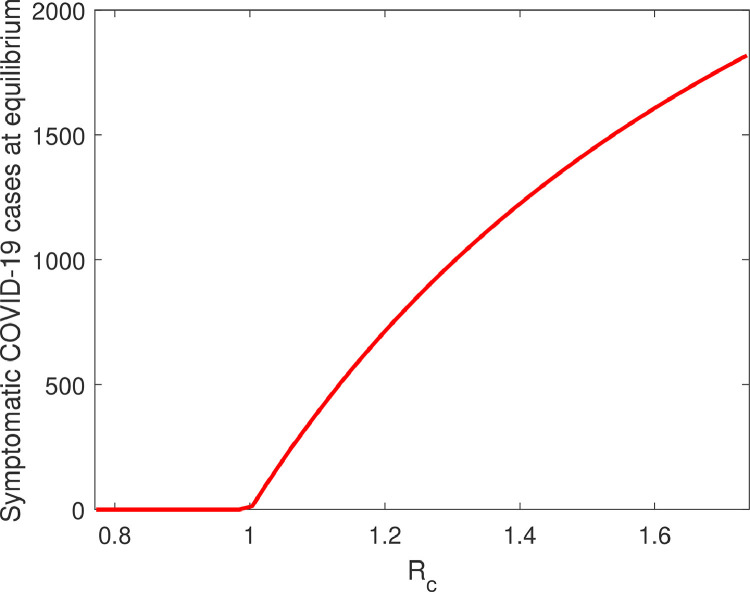
The transcritical bifurcation diagram is depicted in Fig. 2 .

Fig. 2.

Forward bifurcation diagram with respect to $R_c$. All the fixed parameters are taken from Table 1 with ${\gamma }_1=0.0001,$${\gamma }_2=0.0001,$$k_2=0.0632,$${\sigma }_1=0.2158,$${\sigma }_2=0.03$${\sigma }_4=0.4521$ and $0.2<\beta <0.35$.

3.5. Threshold analysis

In this section, the impact of quarantine and isolation is measured qualitatively on the disease transmission dynamics. A threshold study of the parameters correlated with the quarantine of exposed individuals ${\gamma }_1$and the isolation of the infected symptomatic individuals ${\gamma }_2$ is performed by measuring the partial derivatives of the control reproduction number $R_c$ with respect to these parameters. We observe that

$$\begin{array}{cc}\hfill \frac{\partial R_c}{\partial {\gamma }_1}& =\frac{r_Q\beta (k_1+\mu )}{{({\gamma }_1+k_1+\mu )}^2(k_2+{\sigma }_1+\mu )}-\frac{r_A\beta p{k}_1}{{({\gamma }_1+k_1+\mu )}^2({\sigma }_2+\mu )}-\frac{\beta k_1(1-p)}{{({\gamma }_1+k_1+\mu )}^2({\gamma }_2+{\sigma }_3+\mu )}\hfill \\ & +\frac{r_J\beta }{{({\gamma }_1+k_1+\mu )}^2(\delta +{\sigma }_4+\mu )}[\frac{k_2(k_1+\mu )}{k_2+{\sigma }_1+\mu }-\frac{(1-p)k_1{\gamma }_2}{{\gamma }_2+{\sigma }_3+\mu }]\hfill \end{array}$$

so that, $\frac{\partial R_c}{\partial {\gamma }_1}<0$ $(>0)$ iff $r_Q<r_{{\gamma }_1}$ ($r_Q>r_{{\gamma }_1}$) where

$$\begin{array}{cc}\hfill 0<r_{{\gamma }_1}& =\frac{k_2+{\sigma }_1+\mu }{k_1+\mu }[\frac{r_{A}p{k}_1}{{\sigma }_2+\mu }+\frac{k_1(1-p)}{{\gamma }_2+{\sigma }_3+\mu }]\hfill \\ & +\frac{r_J(k_2+{\sigma }_1+\mu )}{(k_1+\mu )(\delta +{\sigma }_4+\mu )}[\frac{(1-p)k_1{\gamma }_2}{{\gamma }_2+{\sigma }_3+\mu }-\frac{k_2(k_1+\mu )}{k_2+{\sigma }_1+\mu }]\hfill \end{array}$$

From the previous analysis, it is obvious that if the relative infectiousness of quarantine individuals $r_Q$ will not cross the threshold value $r_{{\gamma }_1},$ then quarantining of exposed individuals results in reduction of the control reproduction number $R_c$ and therefore reduction of the disease burden. On the other side, if $r_Q>r_{{\gamma }_1},$ then the control reproduction number $R_c$ would rise due to the increase in the quarantine rate and thus the disease burden will also rise and therefore the use of quarantine in this scenario is harmful. The result is summarized in the following way:

Theorem 3.5

For the model(2.8), the use of quarantine of the exposed individuals will have positive (negative) population-level impact if$r_Q<r_{{\gamma }_1}$$(r_Q>r_{{\gamma }_1})$.

Similarly, measuring the partial derivatives of $R_c$ with respect to the isolation parameter ${\gamma }_2$is used to determine the effect of isolation of infected symptomatic individuals. Thus, we obtain

$$\begin{array}{cc}\hfill \frac{\partial R_c}{\partial {\gamma }_2}& =\frac{r_J\beta (1-p)k_1}{({\gamma }_1+k_1+\mu )({\gamma }_2+{\sigma }_3+\mu )(\delta +{\sigma }_4+\mu )}-\frac{r_J\beta (1-p)k_1{\gamma }_2}{({\gamma }_1+k_1+\mu ){({\gamma }_2+{\sigma }_3+\mu )}^2(\delta +{\sigma }_4+\mu )}\hfill \\ & -\frac{\beta k_1(1-p)}{({\gamma }_1+k_1+\mu ){({\gamma }_2+{\sigma }_3+\mu )}^2}\hfill \end{array}$$

Thus, $\frac{\partial R_c}{\partial {\gamma }_2}<0$ $(>0)$ iff $r_J<r_{{\gamma }_2}$ ($r_J>r_{{\gamma }_2}$) where

$$0<r_{{\gamma }_2}=\frac{\delta +{\sigma }_4+\mu }{{\sigma }_3+\mu }$$

The use of isolation of infected symptomatic individuals will also be effective in controlling the disease in the population if the relative infectiousness of the isolated individuals $r_J$ does not cross the threshold $r_{{\gamma }_2}$. The result is summarized below:

Theorem 3.6

For the model(2.8), the use of isolation of infected symptomatic individuals will have positive (negative) population-level impact if$r_J<r_{{\gamma }_2}$$(r_J>r_{{\gamma }_2})$.

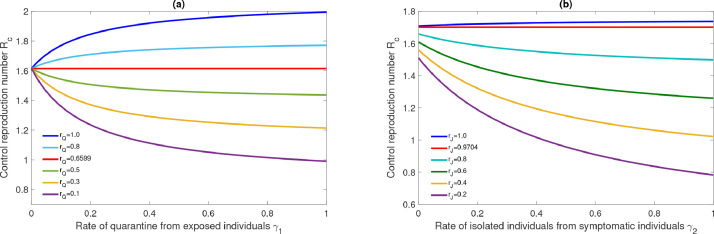
The control reproduction number $R_c$ is a decreasing (non-decreasing) function of the quarantine and isolation parameters ${\gamma }_1$ and ${\gamma }_2$ if the conditions $r_Q<r_{{\gamma }_1}$ and $r_J<r_{{\gamma }_2}$ are respectively satisfied. See Fig. 7(a) and (b) obtained from model simulation in which the results correspond to the theoretical findings discussed.

Fig. 7.

Effect of isolation parameters ${\gamma }_1$ and ${\gamma }_2$ on control reproduction number $R_c$.

3.6. Model without control and basic reproduction number

We consider the system in this section when there is no control mechanism, that is, in the absence of quarantined and isolated classes. Setting ${\gamma }_1={\gamma }_2=0$ in the model (2.8) give the following reduce model

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dS}{dt}}& =& \Pi -\frac{S(\beta I+r_A\beta A)}{\widehat{N}}-\mu S,\hfill \\ \hfill {\displaystyle \frac{dE}{dt}}& =& \frac{S(\beta I+r_A\beta A)}{\widehat{N}}-(k_1+\mu )E,\hfill \\ \hfill {\displaystyle \frac{dA}{dt}}& =& p{k}_{1}E-({\sigma }_2+\mu )A,\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& =& (1-p)k_{1}E-({\sigma }_3+\mu )I,\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}& =& {\sigma }_{2}A+{\sigma }_{3}I-\mu R,\hfill \end{array}$$ (3.7)

Where $\widehat{N}=S+E+A+I+R$. The diseases-free equilibrium can be obtained for the system (3.7) by putting $E=0,A=0,I=0,$ which is denoted by $P_2^0=(S^0,0,0,0,R^0),$ where

$$S^0=\frac{\Pi }{\mu },R^0=0.$$

We will follow the convention that the basic reproduction number is defined in the absence of control measure, denoted by $R_0$ whereas we calculate the control reproduction number when the control measure is in place. The basic reproduction number $R_0$ is defined as the expected number of secondary infections produced by a single infected individual in a fully susceptible population during his infectious period [8], [25], [30]. We calculate $R_0$ in the same way as we calculate $R_c$ by using next generation operator method [54]. Now we calculate the jacobian of $\mathcal{F}$ and $\mathcal{V}$ at DFE $P_2^0$

$$\begin{array}{c}\hfill F=\frac{\partial \mathcal{F}}{\partial X}=\left(\begin{array}{ccc}0& r_A\beta & \beta \\ 0& 0& 0\\ 0& 0& 0\end{array}\right),V=\frac{\partial \mathcal{V}}{\partial X}=\left(\begin{array}{ccc}{\gamma }_1+k_1+\mu & 0& 0\\ -p{k}_1& {\sigma }_2+\mu & 0\\ -(1-p)k_1& 0& {\gamma }_2+{\sigma }_3+\mu \end{array}\right).\end{array}$$

Following [29], $R_0=\rho \left(F{V}^{-1}\right),$ where $\rho$ is the spectral radius of the next-generation matrix ($F{V}^{-1}$). Thus, from the model (3.7), we have the following expression for $R_0$:

$$R_0=\frac{r_A\beta p{k}_1}{(k_1+\mu )({\sigma }_2+\mu )}+\frac{\beta k_1(1-p)}{(k_1+\mu )({\sigma }_3+\mu )}$$ (3.8)

Thus, $R_0$ is $R_c$ with ${\gamma }_1={\gamma }_2=0$. From, the expression of $R_0$ it is clear that it consists of two parts i.e, $\frac{r_A\beta p{k}_1}{(k_1+\mu )({\sigma }_2+\mu )},$ $\frac{\beta k_1(1-p)}{(k_1+\mu )({\sigma }_3+\mu )}$ which come from asymptomatic and symptomatic patients respectively. Also, note that when $p=0$ or all the COVID-19 patients are symptomatic the expression of $R_0$ only have the symptomatic part of the expression. On the other hand, when $p=1$ or all the patients are asymptomatic then the expression of $R_0$ only have the asymptomatic part of the expression. We list few expressions of $R_0$ from existing COVID-19 models in Table 2 . The description of each parameters in the expressions can be found in the respective references. From these expressions, we can observe that the terms in the expression of $R_0$ are determined by the number of infectious compartments in the models. Suwardi et al. [9] has a single term as they have considered one infectious compartment whereas Sardar et al. [50], Monteiro et al. [42] and Monteiro [43] have two terms as they considered both asymptomatic and symptomatic patients. The expression of $R_0$ of our proposed model also has two terms representing contribution from asymptomatic and symptomatic patients. Similarly, Jayrold et al. [10] and Silvio et al. [48] have got three terms in the expression as they considered three infectious compartments in their models.

Table 2.

Some previously reported expressions of $R_0$ for COVID-19.

Study	$R_0$	Epidemiological meaning
Suwardi et al. [9] ($SEIR$)	$\frac{\alpha \beta \mu }{(\mu +\beta )(\mu +\nu )({\mu }_i+\delta +\mu )}$	The term $\frac{\alpha }{\mu +\beta }$ is the contact rate with exposed people. An infected individual spends on average a time $\frac{1}{{\mu }_i+\delta +\mu }$ in the infective compartment before entering in the recovered class. $R_0$ is proportional to $\frac{1}{\nu +\mu }$ which represent the proportion of susceptibles who can not get the disease.
Sardar et al. [50] ($SEAICR$)	$\frac{{\beta }_1\kappa \sigma }{(\mu +\sigma )({\gamma }_2+\tau +\mu )}+\frac{\rho {\beta }_1(1-\kappa )\sigma }{(\mu +\sigma )({\gamma }_1+\mu )}$	The two terms of the expression are due to asymptomatic and symptomatic patients respectively. An exposed individual spends on average a time $\frac{1}{\mu +\sigma }$ in the exposed class before entering in the asymptomatic and symptomatic class with rate $(1-\kappa )\sigma$ and $\kappa \sigma$ respectively. An asymptomatic and symptomatic individual spends on average a time $\frac{1}{{\gamma }_1+\mu }$ and $\frac{1}{{\gamma }_2+\tau +\mu }$ before entering in the hospitalized class.
Jayrold et al. [10] ($SE{I}_a{I}_{s}UR$)	$\omega (\frac{{\beta }_e}{{\delta }_e+{\nu }_e}+\frac{f{\beta }_s}{{\gamma }_s+{\mu }_s+{\nu }_s}+\frac{(1-f){\beta }_a}{{\gamma }_a})\frac{S^{*}}{N^{*}}$	The term $\frac{\omega {\beta }_e}{{\delta }_e+{\nu }_e}$ represents the contact rate with exposed during the average latency period $\frac{1}{{\delta }_e+{\nu }_e}$. The term $\frac{\omega f{\beta }_s}{{\gamma }_s+{\mu }_s+{\nu }_s}$ is the contact rate with symptomatic during the average infection period, and the last one is the part of asymptomatic.
Silvio et al. [48] ($SE{I}_A{I}_S{I}_{D}RD$)	$\frac{\alpha ϵ}{\zeta +{\eta }_A}+\frac{\beta (1-ϵ)}{{\theta }_s+{\eta }_s+\kappa }+\frac{\gamma }{{\theta }_D+{\kappa }_D}[\frac{ϵ}{\zeta +{\eta }_A}{\eta }_A+\frac{1-ϵ}{{\theta }_s+{\eta }_s+\kappa }{\eta }_s]$	An asymptomatic and symptomatic individual spends on average a time $\frac{1}{\delta }$ in the exposed compartment before entering in the infective asymptomatic and symptomatic compartment with rate $ϵ\delta$ and $(1-ϵ)\delta$ respectively, where she/he spends on average a time $\frac{1}{\zeta +{\eta }_A}$ and $\frac{1}{{\theta }_s+{\eta }_s+\kappa },$ occurs with a rate $\beta$. Finally a diagnosed individual, that spends on average a time $\frac{1}{{\theta }_D+{\kappa }_D}$ and can infect with rate $\gamma ,$ can either be originated by an asymptomatic symptomatic individual with rate ${\eta }_A$ and ${\eta }_s$ respectively.
L.H.A. Monteiro et al. [43] ($SAIR$)	$\frac{x{a}_{1}N}{b_1+c_1}+\frac{(1-x)a_{2}N}{b_2+c_2}$	The two terms of the expression are due to asymptomatic and symptomatic patients respectively. The term $\frac{x{a}_{1}N}{b_1+c_1}$ represents the contact rate with asymptomatic during the average time period $\frac{1}{b_1+c_1}$. The term $\frac{(1-x)a_{2}N}{b_2+c_2}$ represents the contact rate with symptomatic during the average time period $\frac{1}{b_2+c_2}$.
L.H.A. Monteiro [42] ($SAIR$)	$|\frac{nN}{2p}+\sqrt{{\left(\frac{nN}{2p}\right)}^2+\frac{m{N}^2}{p}}|$	In this case, two terms of the expression consist of mixed effects from both symptomatic and asymptomatic patients.

3.6.1. Stability of DFE of the model3.7

Theorem 3.7

The diseases free equilibrium (DFE) $P_2^0=(S^0,0,0,0,R^0)$ of the system (3.7) is locally asymptotically stable if $R_0<1$ and unstable if $R_0>1$ .

Proof

We calculate the Jacobian of the system (3.7) at DFE $P_2^0,$ is given by

$$\begin{array}{c}\hfill J_{P_2^0}=\left(\begin{array}{ccccc}-\mu & 0& -r_A\beta & -\beta & 0\\ 0& -(k_1+\mu )& r_A\beta & \beta & 0\\ 0& p{k}_1& -({\sigma }_2+\mu )& 0& 0\\ 0& (1-p)k_1& 0& -({\sigma }_3+\mu )& 0\\ 0& 0& {\sigma }_2& {\sigma }_3& -\mu \end{array}\right)\end{array}$$

Let $\lambda$ be the eigenvalue of the matrix $J_{P_2^0}$. Then the characteristic equation is given by $det(J_{P_2^0}-\lambda I)=0$.

$$\Rightarrow r_A\beta p{k}_1(\lambda +{\sigma }_3+\mu )+\beta k_1\left[(1-p)(\lambda +{\sigma }_2+\mu )\right]-(\lambda +k_1+\mu )(\lambda +{\sigma }_2+\mu )(\lambda +{\sigma }_3+\mu )=0.$$

which implies

$$\frac{r_A\beta p{k}_1}{(\lambda +k_1+\mu )(\lambda +{\sigma }_2+\mu )}+\frac{\beta k_1(1-p)}{(\lambda +k_1+\mu )(\lambda +{\sigma }_3+\mu )}=1=G_2\left(\lambda \right)\left(say\right).$$

We rewrite $G_2\left(\lambda \right)$ as $G_2\left(\lambda \right)=G_{21}\left(\lambda \right)+G_{22}\left(\lambda \right)$

Now if $Re\left(\lambda \right)\ge 0,$ $\lambda =x+iy,$ then

$$\begin{array}{cc}\hfill |G_{21}\left(\lambda \right)|& \le \frac{r_A\beta p{k}_1}{|\lambda +k_1+\mu \parallel \lambda +{\sigma }_2+\mu |}\le G_{21}\left(x\right)\le G_{21}\left(0\right)\hfill \\ \hfill |G_{22}\left(\lambda \right)|& \le \frac{\beta k_1(1-p)}{|\lambda +k_1+\mu \parallel \lambda +{\sigma }_3+\mu |}\le G_{22}\left(x\right)\le G_{22}\left(0\right)\hfill \end{array}$$

Then $G_{21}\left(0\right)+G_{22}\left(0\right)=G_2\left(0\right)=R_0<1,$ which implies $|G_2\left(\lambda \right)|\le 1$.

Thus for $R_0<1,$ all the eigenvalues of the characteristics equation $G_2\left(\lambda \right)=1$ has negative real parts.

Therefore if $R_0<1,$ all eigenvalues are negative and hence DFE $P_2^0$ is locally asymptotically stable.

Now if we consider $R_0>1$ i.e $G_2\left(0\right)>1,$ then

$$\underset{\lambda \to \infty }{lim}{G}_2\left(\lambda \right)=0.$$

Then there exist ${\lambda }^{*}>0$ such that $G_2\left({\lambda }^{*}\right)=1$.

That means there exist positive eigenvalue ${\lambda }^{*}>0$ of the Jacobian matrix.

Hence DFE $P_2^0$ is unstable whenever $R_0>1$. □

Theorem 3.8

The diseases free equilibrium (DFE) $P_2^0=(S^0,0,0,0,R^0)$ is globally asymptotically stable for the system (3.7) if $R_0<1$ and unstable if $R_0>1$ .

Proof

We rewrite the system (3.7)as

$$\begin{array}{cc}\hfill \frac{dX}{dt}& =F_1(X,V)\hfill \\ \hfill \frac{dV}{dt}& =G_1(X,V),G_1(X,0)=0\hfill \end{array}$$

where $X=(S,R)\in R_2$ (the number of uninfected individuals compartments), $V=(E,A,I)\in R_3$ (the number of infected individuals compartments), and $P_2^0=(\frac{\Pi }{\mu },0,0,0,0)$ is the DFE of the system (3.7). The global stability of the DFE is guaranteed if the following two conditions are satisfied:

• 1.For $\frac{dX}{dt}=F_1(X,0),$ $X^{*}$ is globally asymptotically stable,
• 2.$G_1(X,V)=BV-{\widehat{G}}_1(X,V),$${\widehat{G}}_1(X,V)\ge 0$ for $(X,V)\in \widehat{\Omega },$

where $B=D_V{G}_1(X^{*},0)$ is a Metzler matrix and $\widehat{\Omega }$ is the positively invariant set with respect to the model (3.7). Following Castillo-Chavez et al [13], we check for aforementioned conditions.

For system (3.7),

$$\begin{array}{ccc}\hfill F_1(X,0)& =& \begin{array}{c}\Pi -\mu S\hfill \\ 0\hfill \end{array},\hfill \\ \hfill B& =& \begin{array}{ccc}-(k_1+\mu )\hfill & r_A\beta \hfill & \beta \hfill \\ p{k}_1\hfill & -({\sigma }_2+\mu )\hfill & 0\hfill \\ (1-p)k_1\hfill & 0\hfill & -({\sigma }_3+\mu )\hfill \end{array}\hfill \end{array}$$

and

$$\begin{array}{c}\hfill {\widehat{G}}_1(X,V)=\left(\begin{array}{c}{r}_A\beta A(1-\frac{S}{\widehat{N}})+\beta I(1-\frac{S}{\widehat{N}})\\ 0\\ 0\end{array}\right).\end{array}$$

Clearly, ${\widehat{G}}_1(X,V)\ge 0$ whenever the state variables are inside $\widehat{\Omega }$. Also it is clear that $X^{*}=(\frac{\Pi }{\mu },0)$ is a globally asymptotically stable equilibrium of the system $\frac{dX}{dt}=F_1(X,0)$. Hence, the theorem follows. □

3.6.2. Existence and local stability of endemic equilibrium

In this section, the existence of the endemic equilibrium of the model (3.7) is established. Let us denote

$$h_1=k_1+\mu ,h_2={\sigma }_2+\mu ,h_3={\sigma }_3+\mu .$$

Let $P_2^{*}=(\widehat{S},\widehat{E},\widehat{A},\widehat{I},\widehat{R})$ represents any arbitrary endemic equilibrium point (EEP) of the model (3.7). Further, define

$${\lambda }^{*}=\frac{\beta (\widehat{I}+r_A\widehat{A})}{\widehat{N}}$$ (3.9)

It follows, by solving the equations in (3.7) at steady-state, that

$$\begin{array}{cc}\hfill \widehat{S}& =\frac{\Pi }{{\lambda }^{*}+\mu },\widehat{E}=\frac{{\lambda }^{*}\widehat{S}}{h_1},\widehat{A}=\frac{p{k}_1{\lambda }^{*}\widehat{S}}{h_1{h}_2},\hfill \\ \hfill \widehat{I}& =\frac{(1-p)k_1{\lambda }^{*}\widehat{S}}{h_1{h}_3},\widehat{R}=\frac{{\lambda }^{*}\widehat{S}[p{k}_1{\sigma }_2{h}_3+(1-p)k_1{\sigma }_3{h}_2]}{\mu h_1{h}_2{h}_3}\hfill \end{array}$$ (3.10)

Substituting the expression in (3.10) into (3.9) shows that the non-zero equilibrium of the model (3.7) satisfy the following linear equation, in terms of ${\lambda }^{*}$:

$$X{\lambda }^{*}+Y=0$$ (3.11)

where

$$\begin{array}{cc}\hfill X& =\mu h_2{h}_3+\mu p{k}_1{h}_3+\mu (1-p)k_1{h}_2+{\sigma }_{2}p{k}_1{h}_3+(1-p)k_1{\sigma }_3{h}_2\hfill \\ \hfill Y& =\mu h_1{h}_2{h}_3(1-R_0)\hfill \end{array}$$

Since $X>0,$ $\mu >0,$ $h_1>0,$ $h_2>0$ and $h_3>0,$ it is clear that the model (3.7) has a unique endemic equilibrium point (EEP) whenever $R_0>1$ and no positive endemic equilibrium point whenever $R_0<1$. This rules out the possibility of the existence of equilibrium other than DFE whenever $R_0<1$. Furthermore, it can be shown that, the DFE $P_2^0$ of the model (3.7) is globally asymptotically stable (GAS) whenever $R_0<1$.

From the above discussion we have concluded that

Theorem 3.9

The endemic equilibrium$P_2^{*}$is locally asymptotically stable if$R_0>1$.

Proof

A straightforward procedure same as the proof of Theorem 3.4 will prove this theorem. □

4. Model Calibration and epidemic potentials

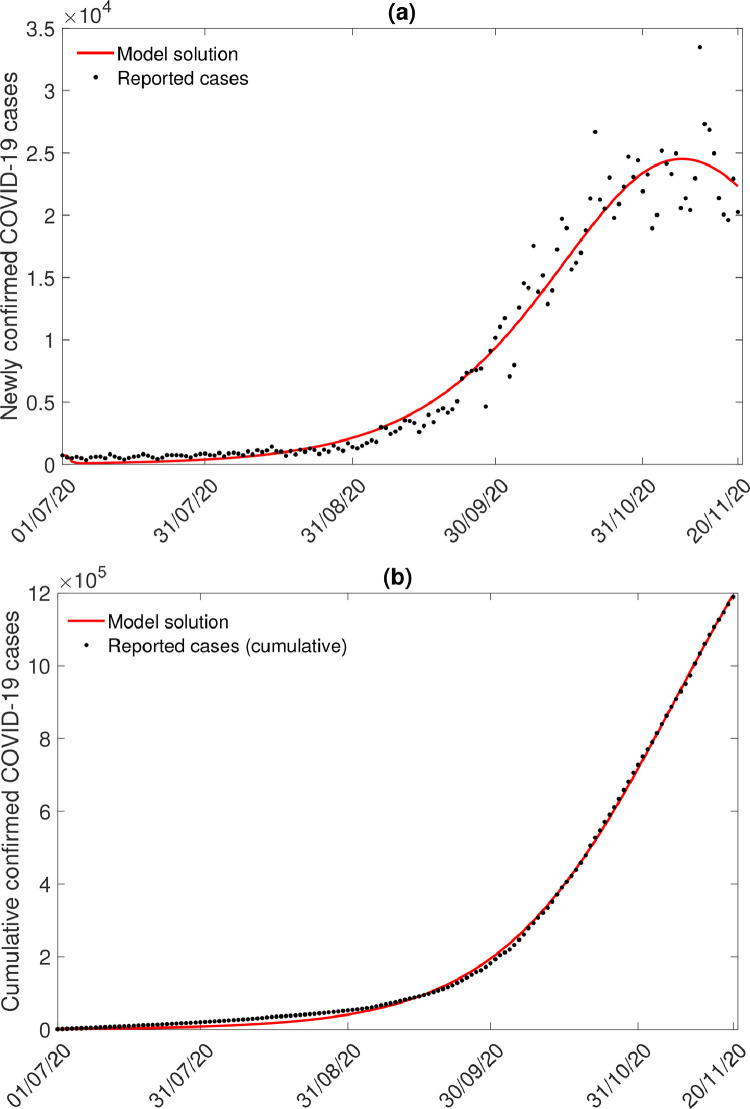
We calibrated our model (2.8) to the daily new COVID-19 cases for the UK. Daily COVID-19 cases are collected for the period 1 July, 2020 - 4 December, 2020 [4]. We divide the 157 data points into training periods and testing periods, viz., 1 July - 20 November and 21 November - 4 December respectively. We fit the model (2.8) to daily new isolated cases of COVID-19 in the UK. Due to the highly transmissible virus, the notified cases are immediately isolated, and therefore it is convenient to fit the isolated cases to reported data.

Also, we fit the model (2.8) to cumulative isolated cases of COVID-19. We estimate the diseases transmission rates by humans, $\beta$, quarantine rate of exposed individuals, ${\gamma }_1,$ isolation rate of infected individual, ${\gamma }_2,$ rate at which quarantined individuals are isolated, $k_2,$ recovery rate from quarantined individuals, ${\sigma }_1,$ recovery rate from asymptomatic individuals, ${\sigma }_2,$ recovery rate from isolated individuals, ${\sigma }_4,$ and initial population sizes. The COVID-19 data are fitted using the optimization function ’fminsearchbnd’ (MATLAB, R2017a). The estimated parameters are given in Table 1. We also estimate the initial conditions of the human population and the estimated values are given by Table 3 . The fitting of the daily isolated COVID-19 cases in the UK are displayed in Fig. 3 .

Table 3.

Estimated initial population sizes for the UK.

Initial values	Value	Source
$S\left(0\right)$	20,341,362	Estimated
$E\left(0\right)$	561	Estimated
$Q\left(0\right)$	2718	Assumed
$A\left(0\right)$	1092	Estimated
$I\left(0\right)$	3	Estimated
$J\left(0\right)$	751	Data
$R\left(0\right)$	10	Assumed

Fig. 3.

(a) Model solutions fitted to daily new isolated COVID cases in the UK. (b) Model fitting with cumulative COVID-19 cases in the UK. Observed data points are shown in black circle and the solid red line depicts the model solutions. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Using these estimated parameters and the fixed parameters from Table 1, we calculate the basic reproduction numbers ($R_0$) and control reproduction numbers ($R_c$) for the UK. The values for $R_0$ and $R_c$ are found to be 1.7291 and 1.5549 respectively. $R_c$ value is above unity, which indicates that they should increase the control interventions to limit future COVID-19 cases.

5. Short-term predictions

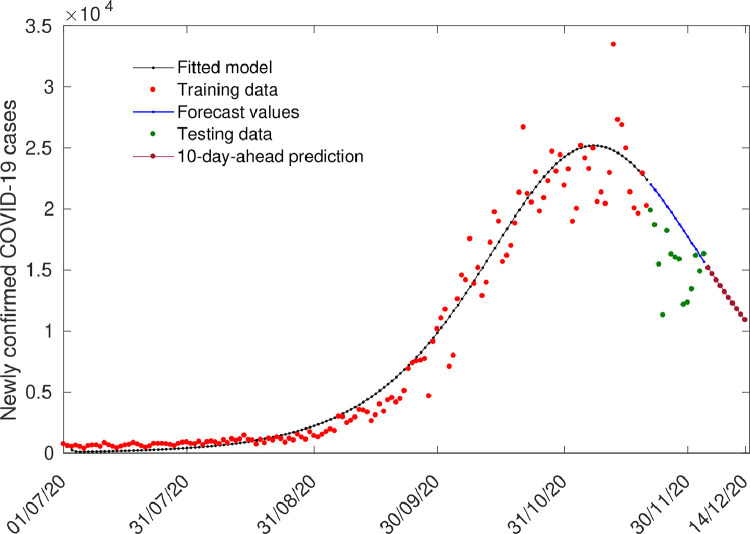
In this section, the short-term prediction capability of the model 2.8 is studied. Using parameters form Tables 1 and 3, we simulate the newly isolated COVID-19 cases for the period 21 November, 2020 - 4 December, 2020 to check the accuracy of the predictions. Next, 10-day-ahead predictions are reported for the UK. The short-term prediction for the UK is depicted in Fig. 4 .

Fig. 4.

Short term predictions for the UK. The blue line represent the predicted new isolated COVID cases while the solid dots are the actual cases. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

We calculate two performance metrics, namely Mean Absolute Error (MAE) and Root Mean Square Error (RMSE) to assess the accuracy of the predictions. This is defined using a set of performance metrics as follows:

Mean Absolute Error (MAE):

$$MAE=\frac{1}{N_p}\sum _{i=1}^{N_p}|Y\left(i\right)-\widehat{Y}\left(i\right)|$$

Root Mean Square Error (RMSE):

$$RMSE=\sqrt{\frac{1}{N_p}{\sum }_{i=1}^{N_p}{(Y\left(i\right)-\widehat{Y}\left(i\right))}^2}$$

where $Y\left(i\right)$ represent original cases, $\widehat{Y\left(i\right)}$ are predicted values and $N_p$ represents the sample size of the data. These performance metrics are found to be MAE=3522 and RMSE=4227. We found that the model performs excellently in case of the UK. The decreasing trend of newly isolated COVID-19 cases is also well captured by the model.

6. Control strategies

In order to get an overview of the most influential parameters, we compute the normalized sensitivity indices of the model parameters with respect to $R_c$. We have chosen parameters transmission rate between human population $\beta ,$ the control related parameters, ${\gamma }_1,$ ${\gamma }_2$ and $k_2,$ the recovery rates from quarantine individuals ${\sigma }_1,$ asymptomatic individuals ${\sigma }_2$ and isolated individuals ${\sigma }_4$ and the effect of diseases induced mortality rate $\delta$ for sensitivity analysis. We compute normalized forward sensitivity indices of these parameters with respect to the control reproduction number $R_c$. We use the parameters from Tables 1 and 3. However, the mathematical definition of the normalized forward sensitivity index of a variable $m$ with respect to a parameter $\tau$ (where $m$ depends explicitly on the parameter $\tau$) is given as:

$$X_m^{\tau }=\frac{\partial m}{\partial \tau }\times \frac{\tau }{m}.$$

The sensitivity indices of $R_c$ with respect to the parameters $\beta ,$ ${\gamma }_1,$ ${\gamma }_2,$ $k_2,$ ${\sigma }_1,$ ${\sigma }_2,$ ${\sigma }_4$ and $\delta$ are given by Table 4 .

Table 4.

Normalized sensitivity indices of some parameters of the model 2.8.

$X_{R_c}^{\beta }$	$X_{R_c}^{{\gamma }_1}$	$X_{R_c}^{{\gamma }_2}$	$X_{R_c}^{k_2}$	$X_{R_c}^{{\sigma }_1}$	$X_{R_c}^{{\sigma }_2}$	$X_{R_c}^{{\sigma }_4}$	$X_{R_c}^{\delta }$
1.0000	0.0964	0.0344	0.0033	0.0402	0.3214	0.1358	0.0005

The fact that $X_{R_c}^{\beta }=1$ means that if we increase 1% in $\beta ,$ keeping other parameters be fixed, will produce 1% increase in $R_c$. Similarly, $X_{R_c}^{{\sigma }_2}=-0.3214$ means increasing the parameter ${\sigma }_2$ by 1%, the value of $R_c$ will be decreased by 0.3214% keeping the value of other parameters fixed. Therefore, the transmission rate between susceptible humans and COVID-19 infected humans is positively correlated and the recovery rate from asymptomatic class is negatively correlated with respect to control reproduction number respectively.

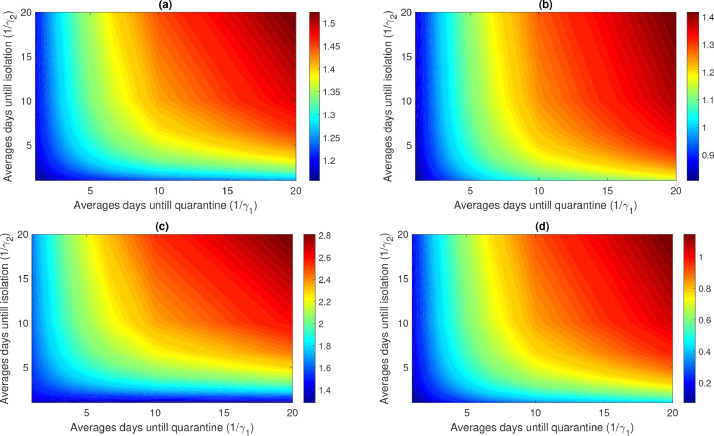
In addition, we draw the contour plots of $R_c$ with respect to the parameters ${\gamma }_1$ and ${\gamma }_2$ for the model (2.8) to investigate the effect of the control parameters on control reproduction number $R_c,$ see Fig. 5 .

Fig. 5.

Contour plots of $R_c$ versus average days to quarantine ($1/{\gamma }_1$) and isolation ($1/{\gamma }_2$) for the UK, (a) in the presence of both modification factors for quarantined ($r_Q$) and isolation ($r_J$); (b) in the presence of modification factors for isolation ($r_J$) only; (c) in the presence of modification factors for quarantined ($r_Q$) only and (d) in the absence of both modification factors for quarantined ($r_Q$) and isolation ($r_J$). All parameter values other than ${\gamma }_1$ and ${\gamma }_2$ are given in Table 1.

The contour plots of Fig. 5 show the dependence of $R_c$ on the quarantine rate ${\gamma }_1$ and the isolation rate ${\gamma }_2$ for the UK. The axes of these plots are given as average days from exposed to quarantine ($1/{\gamma }_1$) and average days from starting of symptoms to isolation ($1/{\gamma }_2$). For both cases, the contours show that increasing ${\gamma }_1$ and ${\gamma }_2$ reduces the amount of control reproduction number $R_c$ and, therefore, COVID cases. We find that quarantine and isolation are not sufficient to control the outbreak (see Fig. 5(a) and (c)). With these parameter values, as ${\gamma }_1$ increases, $R_c$ decreases and similarly, when ${\gamma }_2$ increases, $R_c$ decreases. But, in both cases $R_c>1,$ and therefore the disease will persist in the population (i.e. the above control measures cannot lead to effective control of the epidemic). By contrast, our study shows that when the modification factor for quarantine become zero (so that $r_Q=0$), the outbreak can be controlled (see Fig. 5(b) and (d)). From the above finding, it follows that neither the quarantine of exposed individuals nor the isolation of symptomatic individuals will prevent the disease with the high value of the modification factor for quarantine. This control can be obtained by a significant reduction in COVID transmission during quarantine (that is reducing $rQ$).

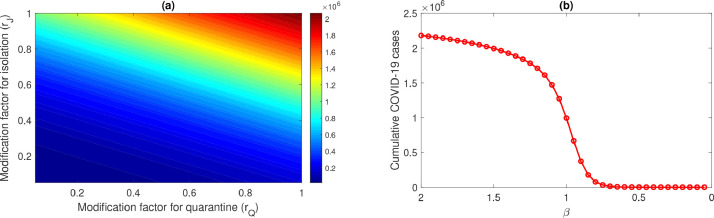
Furthermore, we study the effect of the parameters modification factor for quarantined individuals ($r_Q$), modification factor for isolated individuals ($r_J$) and transmission rate ($\beta$) on the cumulative new isolated COVID-19 cases ($J_{cum}$) in the UK. The cumulative number of isolated cases has been computed at day 100 (chosen arbitrarily). The effect of controllable parameters on ($J_{cum}$) are shown in Fig. 6 .

Fig. 6.

Effect of controllable parameters ${\gamma }_1,$${\gamma }_2$ and $\beta$ on the cumulative number of isolated COVID-19 cases. The left panel shows the variability of the $J_{cum}$ with respect to $\frac{1}{{\gamma }_1}$ and $\frac{1}{{\gamma }_2}$. The right panel shows $J_{cum}$ with decreasing transmission rate $\beta$.

We observe that all the three parameters have a significant effect on the cumulative outcome of the epidemic. From Fig. 6(a) it is clear that decrease in the modification factor for quarantined and isolated individuals will significantly reduce the value of $J_{cum}$. On the other hand, Fig. 6(b) indicates, reduction in transmission rate will also slow down the epidemic significantly. These results point out that all the three control measures are quite effective in the reduction of the COVID-19 cases in the UK. Thus, quarantine and isolation efficacy should be increased by means of proper hygiene and personal protection by health care stuffs. Additionally, the transmission coefficient can be reduced by avoiding contacts with suspected COVID-19 infected cases.

Furthermore, We numerically calculated the thresholds $r_{{\gamma }_1}$ and $r_{{\gamma }_2}$ for the UK. The analytical expression of the thresholds are given in subsection (3.5). The effectiveness of quarantine and isolation depends on the values of the modification parameters $r_Q$ and $r_J$ for the reduction of infected individuals. The threshold value of $r_Q$ corresponding to quarantine parameter ${\gamma }_1$ is $r_{{\gamma }_1}=0.6599$ and the threshold value of $r_J$ corresponding to isolation parameter ${\gamma }_2$ is $r_{{\gamma }_2}=0.9704$.

From Fig. 7(a) it is clear that quarantine parameter ${\gamma }_1$ has positive population-level impact ($R_c$ decreases with increase in ${\gamma }_1$) for $r_Q<0.6599$ and have negative population level impact for $r_Q>0.6599$. Similarly from the Fig. 7(b), it is clear that, isolation has positive level impact for $r_J<0.9704,$ whereas isolation has negative impact if $r_J>0.9704$. This result indicate that isolation and quarantine programs should run effective so that the modification parameters remain below the above mentioned threshold.

7. Conclusions

During the period of an epidemic when human-to-human transmission is established and reported cases of COVID-19 are rising worldwide, forecasting is of utmost importance for health care planning and control of the virus with limited resources. In this study, we have formulated and analyzed a compartmental epidemic model of COVID-19 to predict and control the outbreak. The basic reproduction number and control reproduction number are calculated for the proposed model. It is also shown that whenever $R_0<1,$ the DFE of the model without control is globally asymptotically stable. The efficacy of quarantine of exposed individuals and isolation of infected symptomatic individuals depends on the size of the modification parameter to reduce the infectiousness of exposed ($r_Q$) and isolated ($r_J$) individuals. The usage of quarantine and isolation will have positive population-level impact if $r_Q<r_{{\gamma }_1}$ and $r_J<r_{{\gamma }_2}$ respectively. We calibrated the proposed model to fit daily data from the UK. Using the parameter estimates, we then found the basic and control reproduction numbers for the UK. Our findings suggest that independent self-sustaining human-to-human spread ($R_0>1,$ $R_c>1$) is already present in the UK. The estimates of the control reproduction number indicate that sustained control interventions are necessary to reduce the future COVID-19 cases. The health care agencies should focus on the successful implementation of control mechanisms to reduce the burden of the disease.

The calibrated model then have checked for short-term predictability. It is seen that the model performs excellently (Fig. 4). The model predicted that the new cases in the UK will show a decreasing trend in the near future. However, if the control measures are increased (or $R_c$ is decreased below unity to ensure GAS of the DFE) and maintained efficiently, the subsequent outbreaks can be controlled.

Having an estimate of the parameters and prediction results, we performed control intervention related numerical experiments. Sensitivity analysis reveals that the transmission rate is positively correlated and quarantine and isolation rates are negatively correlated with respect to control reproduction number. This indicates that increasing quarantine and isolation rates and decreasing transmission rate will decrease the control reproduction number and consequently will reduce the disease burden.

While investigating the contour plots 5, we found that effective management of quarantined individuals is more effective than management of isolated individuals to reduce the control reproduction number below unity. Thus if limited resources are available, then investing in the quarantined individuals will be more fruitful in terms of reduction of cases.

Finally, we studied the effect of modification factor for quarantined population, modification factor for isolated population and transmission rate on the newly infected symptomatic COVID-19 cases. Numerical results show that all the three control measures are quite effective in reduction of the COVID-19 cases in the UK (Fig. 6). The threshold analysis reinforce that the quarantine and isolation efficacy should be increased to reduce the epidemic (Fig. 7). Thus, quarantine and isolation efficacy should be increased using proper hygiene and personal protection by health care stuffs. Additionally, the transmission coefficient can be reduced by avoiding contacts with suspected COVID-19 infected cases.

In summary, our study suggests that COVID-19 has a potential to be endemic for quite a long period but it is controllable by social distancing measures and efficiency in quarantine and isolation. Moreover, if limited resources are available, then investing in the quarantined individuals will be more fruitful in terms of the reduction of cases. The ongoing control interventions should be adequately funded and monitored by the health ministry. Health care officials should supply medications, protective masks and necessary human resources in the affected areas.