Are dishonest politicians more likely to be reelected? A Bayesian view

Politicians who lie are more likely to be reelected. That is what Janezic and Gallego (1) conclude. They asked 816 Spanish mayors to toss a coin, with only heads resulting in a desired personalized report of the study results. Mayors reported heads more often (68%) than expected by chance (50%), and reporting heads significantly predicted reelection in the subsequent elections. However, for the conclusion the authors rely exclusively on the P value. In a Bayesian reanalysis we demonstrate that the data do not warrant the original conclusions.

Relying on P values has several disadvantages, including reliance on an arbitrary cutoff point, with small differences in P values leading to very different conclusions (2). Consider, for instance, the four statistical models used by Janezic and Gallego (1) (Table 1). When relying on the conventional alpha = 0.05, the reported coin toss significantly predicts reelection rates only without controlling for any confounds (model 1), but not with increasing control for possible confounders (models 2, 3, and 4).* For middling P values such as 0.03 obtained in model 1—which Janezic and Gallego base their conclusion on—the null hypothesis does not predict the observed data much worse than the alternative hypothesis (5), and rejection of the null may be premature.

Table 1.

Does dishonesty predict reelection?

	Model 1 (no controls); n = 758	Model 2 (cf. model1 but now controlling for several variables, e.g. actually running for reelection); n = 754	Model 3 (cf. model 2 but additionally controlling for interaction between reporting heads and competitiveness elections); n = 754	Model 4 (cf. model 1 but additionally excluding mayors who did not actually run for reelection); n = 624
Statistical significance (P value linear regression)	0.03	0.08	0.07	0.06
Effect size (eta2)*	0.01	0.00	0.00	0.01
BF01 (Bayes factor Bayesian linear regression)	1.17	2.98	2.75	1.56

P values, effect sizes, and Bayes factors for the four regression analyses used by Janezic and Gallego (1). Models 1 through 4 are exactly the same as those reported by the authors in table 2 of ref. 1. While the outcome variable is binary (heads or tails), we followed the authors’ choice for a linear regression.

^*Because the P value does not speak to the magnitude of the effect, the additional reporting of effect size measures has been recommended (7). Table 1 shows that eta²—which can be interpreted as proportion of explained variance—is close to zero, across all models. A benefit of Bayesian analyses over effect size measures is the ability to differentiate absence of evidence from evidence of absence (the larger BF₀₁, the stronger the evidence for the null; ref. 8).

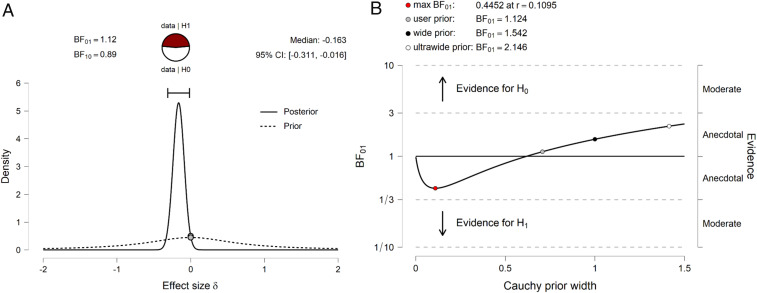
Moving beyond the P value, a Bayesian analysis allows the quantification of evidence by comparing the predictive performance of the null hypothesis against that of the alternative hypothesis (6). Fig. 1A shows that the Bayesian analysis undercuts the authors’ conclusions—the null hypothesis predicts the data about as well as the alternative hypothesis, a pattern that holds irrespective of whether the alternative hypothesis favors small or large effect sizes, the prior plausibility of the hypothesis, and specific data-analytic decisions (Table 1 and Fig. 1B). In sum, the Bayesian analyses indicate that the reported P values reflect an absence of evidence and do not provide statistical backing for strong claims that could harm people’s trust in politicians.

Fig. 1.

Results of the Bayesian independent sample t test. (A) A plot of the prior (dashed line; a Cauchy distribution with width r = 0.707) and the posterior (solid line) and the corresponding Bayes factor. (B) The results of a robustness check across a wide range of prior specifications.

Of note, money was not used as an incentive in the study because it led to strong complaints during pilot testing: Politicians were offended and wanted to avoid accusations of corruption. Perhaps, then, this should have been a signal that politicians are not as deceptive as claimed by the authors.

Data Availability.

We used the data file posted by the authors in Harvard Dataverse at https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/MPAZUD. The JASP files and the R scripts of all analyses reported in our paper can be found in Open Science Framework at https://osf.io/zbxkg/.