Anionic electron within an electride was visualized with atomic resolution using differential phase-contrast imaging.
Abstract
Electrides are an unusual family of materials that feature loosely bonded electrons that occupy special interstitial sites and serve as anions. They are attracting increasing attention because of their wide range of exotic physical and chemical properties. Despite the critical role of the anionic electrons in inducing these properties, their presence has not been directly observed experimentally. Here, we visualize the columnar anionic electron density within the prototype electride Y5Si3 with sub-angstrom spatial resolution using differential phase-contrast imaging in a scanning transmission electron microscope. The data further reveal an unexpected charge variation at different anionic sites. Density functional theory simulations show that the presence of trace H impurities is the cause of this inhomogeneity. The visualization and quantification of charge inhomogeneities in crystals will serve as valuable input in future theoretical predictions and experimental analysis of exotic properties in electrides and materials beyond.
INTRODUCTION
Electrides are a unique class of compound materials that comprise a framework of cation and anion sublattices with a net positive effective charge that is compensated by “anionic electrons” that are loosely bonded and localized at interstitial sites, forming an effective anion sublattice (1–6). Starting in the 1980s, electrides were studied as bulk materials, with several seminal papers highlighting their potential for unconventional physical and chemical properties (1–6). In the past decade, electrides became the focus of a rapidly growing number of papers with the discovery of layered electrides (7, 8), in which the anionic electrons form sheets in the van der Waals gaps between atomic layers, exhibiting very high electron mobility, very small work function, and strong magnetic anisotropy. At about the same time, electrides with anionic electrons localized in one-dimensional (1D) channels gained prominence (9, 10). Very recently, several electrides have been predicted to feature topological behavior (11–13). Overall, anionic electrons in electrides have been demonstrated to exhibit catalytic activity (9, 14, 15), high mobility and unconventional magnetism (7, 8), superconductivity (16, 17), nontrivial topological behavior (11–13), and strong correlations (18) and to behave like solvated ions in solutions (19). Electrides have also been demonstrated to be good for storing hydrogen (20, 21). All these features nurture expectations for real applications. However, electrides have so far been characterized only with macroscopic experiments, such as measurements of the work function (1, 2, 5, 7), while the highly localized anionic charge density has only been studied theoretically (4, 6, 11, 22–24).
Aberration-corrected scanning transmission electron microscopy (STEM) routinely achieves sub-angstrom resolution and has been applied to directly characterize the structural, chemical, and bonding properties of materials at the atomic scale (25–27). While conventional STEM techniques are insensitive to local variations in the charge density, phase-contrast imaging, such as inline electron holography, recently demonstrated the capability to visualize a 2D electron gas with a spatial resolution of several nanometers (28, 29). Concurrently, differential phase contrast (DPC) in STEM, which can be obtained by using either segmented detectors (30–32) or 4D-STEM data sets from a pixelated detector (33, 34), has recently been shown to map local electric fields and charge densities at an unprecedented sub-angstrom spatial resolution (30, 31, 33–36). That capability renders STEM-DPC a powerful potential technique for probing the atomic-scale localization of the charge density at anionic sites in electrides.
In this work, we use STEM-DPC to directly probe the charge density in the interstitial columns of Y5Si3, a prototype electride, using a pixelated detector (or 4D-STEM). Y5Si3 contains spatially localized electrons within 1D channels of ~4 Å diameter (9). Previous theoretical calculations determined that these electrons are loosely bonded, occupying electronic states near the Fermi energy, leading to catalytic reactivity for Y5Si3 (9) and exotic quantum properties, such as superconductivity and Mott-insulating behavior in similar structures (17, 18, 37). Here, we use STEM-DPC to analyze the total charge density in Y5Si3 and, more specifically, electrons that accumulate at the interstitial columns surrounded by hexagonal rings of six Y atoms. The STEM-DPC results are complemented by density functional theory (DFT) calculations of the electric field and charge density, yielding good agreement between the theoretical results and the experimental data averaged over a large number of columns. However, by analyzing a large field of view of the electride, we find an unexpected variance in the observed anionic charge density at different interstitial columns. DFT simulations suggest that the likely origin of the observed inhomogeneities are H impurities, which are known to be ubiquitous in materials, but often difficult to detect in small concentrations.
RESULTS
Crystal structure of Y5Si3
Y5Si3 crystallizes in a hexagonal Mn5Si3-type structure with the P63/mcm space group. Its structure in the [001] projection (Fig. 1A) shows six yttrium (Y) atomic columns forming hexagonal rings, each of which is composed of two alternating staggered layers of three Y triangles along the [001] projection. We have marked these atoms as YR on the schematic and the other Y sites as Y1 to help distinguish between the two for the remainder of the article. The centers of the Y rings form an interstitial column with a diameter of ~4 Å.
Fig. 1. The crystal structure of electride Y5Si3.
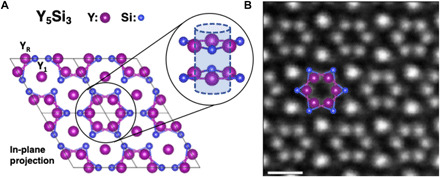
(A) Schematic of the Y5Si3 structure in the [001] projection. Black solid boxes indicate unit cells. Inset circles: Projected and side views of a hexagonal Y ring, with the center forming a column of electrons. (B) HAADF image of Y5Si3 with overlaid atoms defining an interstitial electron column. Scale bar, 5 Å.
Y5Si3 crystals were prepared by arc-melting high-purity Y and Si sources, following Lu et al. (9). A powder x-ray diffraction pattern (fig. S1) revealed the synthesized Y5Si3 as being a single-phase system in the as-cast ingot, with refined lattice parameters [a = 8.4087(1) Å and c = 6.3422(1) Å] that are consistent with those in a previous report (9). The Y5Si3 phase was air stable and water durable, as reported by Lu et al. (9). Ground fine powders were dispersed onto TEM grids in a helium-filled glovebox for the STEM experiments. TEM specimens are exposed to air during specimen loading, which is about 3 min.
Electric field and charge density maps in Y5Si3
Figure 1B shows a high-angle annular dark-field (HAADF) image for a 3 nm × 3 nm region of Y5Si3 oriented along the [001] axis. Owing to the Z-contrast nature of HAADF imaging (where Z is the atomic number), the intensity increases as the total number of atoms and/or their atomic number increase in each column. Thus, the brightest spots in the HAADF are the Y1 sites, which have double the number of Y atoms per unit cell as the YR sites. The YR atoms of the hexagonal ring are visible (and marked in the schematic in Fig. 1B), while the Si atoms are not observed in the HAADF images because of their proximity to the heavier Y atoms. The invisibility of Si atoms in HAADF images is confirmed by STEM image simulations, as shown in fig. S2.
In the DPC experiment, the electron beam is rastered across the region of interest (ROI) and the convergent-beam electron diffraction (CBED) pattern is measured by a high-speed pixelated detector to form a 4D-STEM dataset. Because only the direct beam is used for 4D-STEM, a HAADF image can be acquired simultaneously without disrupting the DPC acquisition. For each probe position in the 4D-STEM dataset, the gradient of the electrostatic potential, i.e., the electric field in the sample, can be determined by measuring the shifts in the center of mass (CoM) of the CBED pattern. For thin objects, CoM shifts are proportional to the electric field experienced by the incident electron beam, allowing atomic-scale mapping of the local electric fields and charge densities (33, 35, 38).
Figure 2 shows a DPC acquisition of Y5Si3 with an interstitial column in the middle. The simultaneously acquired HAADF image is shown in Fig. 2A. A schematic of how different signs of charge influence the CBED pattern and result in CoM shifts is shown in Fig. 2B; near a localized positive charge the incoming electron beam experiences a Coulomb attraction, whereas near a localized negative charge density the electron beam experiences Coulomb repulsion, while both result in a measurable shift of the distribution of electrons within the central disc of the CBED pattern.
Fig. 2. Differential phase contrast in Y5Si3.
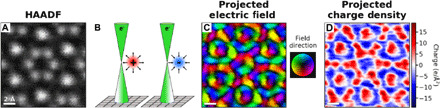
(A) HAADF image of an interstitial column in Y5Si3. (B) Schematics for beam interaction with positive and negative charge densities generating CoM shifts. (C) Projected magnitude and direction of the electrostatic field in the sample as obtained from the CoM shifts. (D) Charge density derived from the divergence of the CoM shifts. The charge density color scale displays positive values on a white-to-red scale, negative values on a white-to-blue scale, and net zero charges as white. Note that the bonding electrons between Y and Si atoms are not discernible in (D) because of the broadened nuclear charges. The interstitial electrons, which are the focus of this work, are seen in blue in the column at the center of the map.
The deflection of the beam in milliradians can be converted to a momentum transfer for each probe position, and for thin specimens (less than 5 nm), the momentum transfer can be quantitatively related to the projected electric field via Ehrenfest’s theorem (38–40). Using position-averaged CBED (PACBED) from the dataset, we measured our sample to be ~7 unit cells thick (corresponding to a thickness of 4.4 nm that is supported by electron-energy loss spectroscopy log-ratio analysis) (see figs. S3 and S4 for more details), allowing us to convert the CoM shifts into the projected electric field of the electride, as shown in Fig. 2C.
At the Y1 sites, we observe the characteristic DPC profile of an atomic column corresponding to highly localized positive charge: a toroidal intensity profile, centered at the nucleus, with a radially outward directional profile. Although the CoM shifts corresponding to each probe position are the combined result from the electron cloud, the nuclei, and chemical bonding, it is the highly localized positive nuclear charges that dominate the atomic columns. However, the interstitial column is well isolated from its nearest atoms, i.e., YR atoms. The distance between the interstitial column center to its nearest YR columns is ~2.05 Å in the beam projection. The electric field surrounding the interstitial column center—i.e., the centers of the YR hexagonal ring—has the same toroidal intensity profile but with a radially inward directional profile, indicating that the region contains spatially localized negative charge.
The projected electric field vectors can be converted to the projected charge density through Gauss’s law, allowing us to examine the localization of charges directly and quantitatively, as plotted in Fig. 2D. As expected, the Y1 and YR sites are positive, corresponding to the high proton density, and are maximized at the positions of the nuclei, while in the interstitial column we observe a distinct negative charge density, consistent with the theoretically predicted anionic electrons for the electride. We note that such an electric field profile could also be produced simply from probe tails interacting with the nuclei surrounding the site, as was reported previously for graphene (32). However, in this case, the contributions from the surrounding Y ring are mitigated because the implemented experimental probe size is ~1 Å (full width at half maximum), while the distance between the six YR and the center of the interstitial site is much larger, ~2 Å. To confirm the detection of anionic electrons, comparisons of DPC experimental results with the simulated charge density from DFT calculations can provide a trustworthy view of the charge density distribution in materials (34, 38, 39).
Comparisons of DPC measurements with simulated charge density from DFT
To better understand the DPC measurements, DFT calculations were performed to determine the charge density in the interstitial columns in Y5Si3. As shown in fig. S5, calculations confirm the presence of localized electrons in the interstitial columns. These interstitial electrons mainly sit within 1 eV from the Fermi energy (fig. S6) and are largely contributed by anionic electrons, as reported by Lu et al. (9).
Validation of DPC measurements is performed by comparing the experimental observations of an interstitial unit cell (Fig. 3A) with the total charge density map calculated using DFT calculations (Fig. 3B), which has been proven to be an effective method. Here, the DFT total charge density map (Fig. 3B) is constructed by combining the electron density (obtained directly from the DFT calculation) with the proton density (obtained from positions and charges of the point nuclei in the projected field of view). Both the electron and proton densities were convolved with a probe function to match the spatial resolution of the electron beam, before being combined to form the total charge density (see detailed methods in fig. S7). Pseudopotentials, which treat the nuclei and core electrons together as screened nuclei with finite radii, were used in calculations. All-electron DFT calculations were also performed to validate the use of pseudopotentials. As shown in fig. S8, the electric field profile and electron density at the interstitial region are both nearly identical to the results obtained from the pseudopotential calculations, confirming the reliability of the calculations.
Fig. 3. Quantitative comparison to theory.
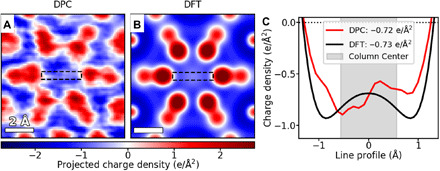
The total charge density in an interstitial unit cell of Y5Si3 as determined by (A) DPC and (B) DFT showing a strong qualitative match for the entire unit cell charge profile. (C) Line profiles [across the anionic column, from the regions highlighted with dashed lines in (A) and (B)] for both methods. The average charge density is calculated for the center (1-Å radius) region (marked by the gray area) of each interstitial column, demonstrating an excellent quantitative match between theory and experiment.
As shown in Fig. 3, the charge density map from DPC measurements matches well with that from DFT calculations: Both exhibit similar charge density profiles around a single unit cell; both consist of highly localized positive charge densities of the nuclei at each atomic site; both show a constantly negative charge density throughout the interstitial column; and both resolve the same spacing distances between the Y1 site and YR/Si atoms. These agreements are encouraging, as they indicate that the directions of the CoM shifts are consistent with the gradient of the potential. It has been shown that for samples that are too thick to perform quantitative DPC, the direction of the measured field tends to deviate notably (38).
Quantitative comparisons between DFT and DPC results are shown in Fig. 3C, where line profiles of the respective charge densities across the interstitial column are compared. While the DPC profile shows a slight asymmetry, the average experimental charge density at the column center is in excellent agreement with the calculated value, −0.73 e/Å2 for DFT and −0.72 e/Å2 for DPC, respectively. Methods of finding the center of the interstitial columns and averaging the column charge density are based on atomic positions obtained from corresponding simulated bright-field images and are described in detail in fig. S9. Results in Fig. 3 therefore demonstrate that DPC is sufficiently sensitive to probe local charge densities at the atomic scale, and comparisons of DPC and DFT measurements provide quantitative information of localized anionic electrons in electrides.
It is noted that, in contrast to the interstitial sites, relatively large intensity differences between DFT and DPC measurements are observed on Y sites. This disparity is largely induced by the dynamic scattering effect in electron imaging and the pseudopotentials adopted in the DFT calculations, because the former imposes a more dominant effect on heavy elements compared to light elements (38, 41, 42), while the latter treats the nuclei and core electrons together as screened nuclei with finite radii. While these factors likely do limit the quantitative comparison between the DPC and DFT results at the atomic sites, the region of the electride that we care most about, namely, the anionic electron columns, is spatially isolated from the atomic nuclei and is not influenced by dynamic scattering in this case.
Inhomogeneity of anionic charge density in Y5Si3
The ability to quantitatively probe the electrons at the atomic scale allows us to examine the distribution of anionic electrons within the specimen. The charge density map of a relatively large region, shown in Fig. 4A, reveals an unexpected phenomenon—the presence of a qualitative and quantitative inhomogeneity in the charge density profile across the different interstitial columns. Four distinct unit cells were highlighted in Fig. 4A for a further quantitative comparison. Horizontal line profiles of the average charge density in each unit cell are plotted against the corresponding profile from the DFT, as shown in Fig. 4 (B to E). The variation of charge density at the anionic electron sites (the intensity of the middle of the line profile) can be clearly seen. Unit cells C1 and C2 (Fig. 4, B and C) show a close quantitative match with the DFT column charge density, similar to that we analyzed in Fig. 3. Instead, unit cells C3 and C4 (Fig. 4, D and E) present a nearly neutral charge density at the center of the anionic column and deviate from the expected negative charge density. Quantitative analysis of spatial averaging of the charge densities within the center region of 1-Å radius allows us to further determine the average charge density of each cell to be 0.76, 0.75, 0.23, and 0.39 e/Å2, respectively. Such an intensity variation suggests that most anionic columns have the predicted negative electron density, while some sites deviate from the pristine anionic charge density and show a lowered electron charge density. Further, these results also demonstrate that DPC not only is sensitive enough to probe small charge densities at the atomic scale but also enables direct atomistic analysis of the charge density in electrides through the combination with DFT calculations.
Fig. 4. Inhomogeneity of anionic charge density of Y5Si3.
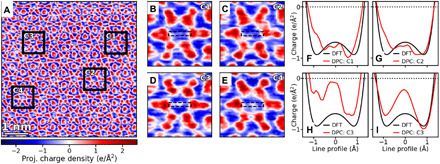
(A) Charge density map of a large area of Y5Si3 showing an inconsistent profile across the center of the interstitial columns. (B to E) Zoomed-in views of columns having both the uniform negative electron density of the electride (B and C) and an inhomogeneity in the anionic electrons observed across the entire dataset (defined by a sharp peak of close to neutral charge density at interstitial column center) (D and E). (F to I) Line profiles across the column centers compared to the DFT line profile from Fig. 3, demonstrating that columns that do not show the inhomogeneity peak match quantitatively with the predicted DFT charge density (F and G), and the ones that have the inhomogeneity show the sharpest difference directly at the column center (H and I).
It is recognized that experimental artifacts could potentially be present in the measurements, but they are not likely to be the cause of the inhomogeneous charge density. First, the heterogeneity is randomly distributed across the 36 columns, while experimental artifacts, primarily induced by specimen thickness or beam illumination conditions, would vary in a rather continuous way. For instance, potential errors induced by beam tilts from scanning would induce systematic differences in the electric field between the top-left and bottom-right corners in each experimental map and introduce approximately the same effect to the interstitial columns as to their nearby atoms, neither of which was observed in our experimental data, as shown in Fig. 4A and figs. S10, S12, and S13.
In addition, no corresponding qualitative changes to the Y or Si intensities are associated with the DPC charge density variation in anionic columns, as shown in Fig. 4 (B to E) and fig. S10, where quantitative charge density of anionic columns and their surrounding YR from a larger region of the specimen are shown to confirm that there is no correlation between the column and its surrounding YR charge densities. Such an independence between the variations in interstitial columns and their neighboring YR columns again indicates that electron beam (e.g., scanning noise and beam tilts), specimen thickness, and surface contamination are unlikely to be the cause.
Moreover, the variation in charge density distributions is higher for Y columns compared to that of interstitial columns, which were calculated to be ±35% for one of the YR columns and ±19% for the interstitial columns, respectively (fig. S11), showing that the inhomogeneity observed among the interstitial columns is genuine. Further validation of the presence of charge variation among anionic columns is obtained by examining charge density maps from specimen regions with different thickness and using multiple different experimental conditions (fig. S12). The inhomogeneity is observed randomly distributed across the different columns in every dataset, demonstrating that the effect can be observed repeatably and that it is real.
Furthermore, the inhomogeneity among the interstitial columns is also proved not to originate from scanning noise, as shown in fig. S13, which overlays the field shift directions on top of the charge density maps for a single unit cell that exhibits deviated charge density and for a unit cell that features the expected charge density. The field directions show that the charge density profile is consistent in both the fast-scanning (x direction) and slow-scanning (y direction) directions. These extensive tests and discussions indicate that while the presence of these potential effects cannot be completely excluded from our DPC experiments, neither of them could be the key cause of the observed inhomogeneity. Instead, such a large inhomogeneous distribution should be associated with a real feature in the material itself.
Origin of charge density inhomogeneity in anionic columns
The column-resolved inhomogeneity could not have been observed in other experiments on electride materials, because, so far, only macroscopic techniques, which are insensitive to these local variations, have been used to characterize the presence of anionic charges. Potential origins of the inhomogeneity in anionic columns are lattice defects in YR sites or impurity atoms at anionic sites. The contrast variation of YR atoms in STEM-HAADF images (e.g., Fig. 1B and figs. S2 and S3) is very small, while a missing YR atom should be clearly visible in STEM images if present, considering the specimen thickness, which only contains seven atoms in total per YR column. Impurity atoms are potentially present in the interstitial sites. Considering the zero contrast in STEM-HAADF and the small contrast in DPC images, the only possible impurity is hydrogen.
To illustrate the possibility that H atoms in the interstitial columns cause the observed inhomogeneity, we calculate the total charge density via DFT in the presence of different numbers of H atoms per interstitial column. Figure 5 (A to F) shows charge density plots in the cases of 0, 1, 2, 5, 10, and 20 H atoms per 10 unit cells, hence fractional values of 0, 0.1, 0.2, 0.5, 1, and 2 H atoms per interstitial site or half those values per formula unit (additional details shown in fig. S14). It can be seen that the charge density observed in the center of the column is sensitive to H concentrations. More critically, the incorporation of H results in a partial charge cancellation at the very center of the interstitial columns that is similar to the inhomogeneity observed in DPC. These total charge density maps are therefore directly comparable to the experimental maps obtained from DPC imaging. The intensity line profiles across their anionic columns are then plotted in Fig. 5G, and an apparent dependence of the charge density at the anionic site on the concentration of H can be seen. The charge density values averaged at the center of these reference interstitial columns (1-Å radius region) and their polynomial fits are further plotted in Fig. 5H, showing a nearly linear relationship between charge density and the concentration of H/site.
Fig. 5. Quantitative charge density maps of Y5Si3 with various H integrations.
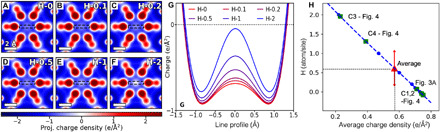
(A to F) DFT calculated charge density maps (after probe convolution) with the integrations of 0, 0.1, 0.5, 1, and 2 H atoms per interstitial layer. (G) Line profiles across the column centers in (A) to (F), showing the dependence of charge density on the concentration of H at the anionic site. (H) Plot of average charge density within the central region (1-Å radius) of the interstitial column versus H concentrations based on (A) to (F). A nominal polynomial fit of the calculated charge density data (blue dots) is shown by a dashed blue curve. The experimental interstitial cells highlighted in Figs. 3 and 4 are plotted as green squares on this nominal line. The red triangle symbol represents the average H concentration in Y5Si3 based on the experimental DPC of Fig. 4A, and its error bar is presented by the SD of all analyzed interstitial cells.
We can then use this relationship as a reference to estimate the H concentration of each single interstitial column in the specimen. The interstitial columns analyzed in Figs. 3 and 4 are plotted on this line to establish estimates for the H incorporation. The unit cells in Fig. 3, as well as those in Fig. 4 (B and C), are apparently pristine (zero H), while those in Fig. 4 (D and E), which showed a near neutral charge density at the column center, are estimated to have about 1.2 H and 1.9 H per interstitial site, respectively. Moreover, the average H integration of all interstitial columns in Fig. 4A can be found on the plot as ~0.6 H atom/site, on the basis of its average charge density of −0.56 e/Å2 (fig. S11). In view of the ultrahigh synthesis temperature (>2000°C) and a very short time ambient exposure (~3 min) of the specimen, such a high fraction per site indicates that Y5Si3 incorporates H atoms quite easily. This result is consistent with an earlier report that, under high H2 pressure and at an elevated temperature, the H concentrations in Y5Si3 can be as high as six per formula unit (20). The energy barrier for a H atom to enter the interstitial column from the surface, calculated by manually stepping the H atom out of the crystal using DFT, is ~0.5 eV (fig. S16), which is an upper bound so that more sophisticated calculations are not necessary. Such a barrier is sufficiently low for H to enter the lattice at room temperature, explaining experimental observations. The possibility of carbon contaminants, a common phenomenon during TEM observations, can be excluded because of the high positive contrast that even one single carbon atom can induce (fig. S15). Electronic excitations at room temperature can also be ruled out, because the density of excited electrons is relatively small even if one assumes that electronic excitations are local as opposed to Bloch-like. Therefore, H integration is most likely the cause for the inhomogeneity observed.
Inelastic neutron scattering (INS) spectroscopy (see Materials and Methods) was used to provide direct evidence for the presence of H in samples prepared using the same synthesis conditions and experiencing similar ambient exposure as the STEM sample. The result is shown in Fig. 6. To identify the peak position contributed by H, DFT phonon calculation was performed using Phonopy (43) for pristine Y5Si3 and 0.5H-Y5Si3. The results were used as input to the OCLIMAX software (44) to simulate INS spectra. The experimental spectrum is compared with the simulated spectra in Fig. 6. Here, we see that below ~350 cm−1 the vibrational response is dominated by Y and Si vibrational modes, and an excellent match is observed between the experiment and both the hydrogenated and pristine simulations. However, above 350 cm−1, no significant vibrational modes are observed in the pristine simulation, but in the hydrogenated simulation and the experiment, we see significant vibrational intensity in this regime, confirming the presence of a significant concentration of H in the material. The possibility of these two distinctive peaks originating from surface absorption of OH can be ruled out, as the typical frequency range for the vibration band of surface OH is 400 to 1000 cm−1, with strong intensities at lower frequencies, and then decays with increasing frequency, a peak profile quite different from the experimental spectrum (45). The presence of two peaks observed in a similar frequency range in the experimental spectra proves the existence of H in the sample.
Fig. 6. Inelastic neutron scattering spectroscopy.
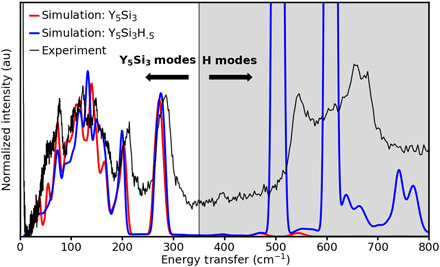
Comparison of the measured INS spectrum with the simulated spectra for Y5Si3 and Y5Si3H0.5. au, arbitrary unit.
Using the simulations in Fig. 6, we estimated the H concentration in the sample, as measured by INS to be of order 0.2 H per site, which is within the error bars of the value of the DPC quantification shown in Fig. 5H, 0.6 ± 0.5 H per site (there exists one site per two formula units). We note that the STEM experiments are performed on the absolute thinnest sample area (thickness, ~5 nm), while the powder used for INS has predominantly micrometer-scale dimensions (fig. S17). Thus, the surface-to-volume ratio could play a significant role in the difference between the INS and DPC values. However, both techniques strongly indicate that a high concentration of hydrogen is present in the material and support the conclusion that H is the origin of the observed inhomogeneity in the measured anionic charge density.
DISCUSSION
Our knowledge on anionic electrons in electrides, including their origin, distribution, and function, is still in its infancy. This work provides a technique that directly visualizes and quantifies anionic electrons, providing an unprecedented tool to the research of electrides. Detection and quantification of charge variation at anionic electron sites that is revealed and confirmed in this work can be used as input to the analysis of the exotic properties in electrides, in both experimental and theoretical studies, to help understand electrides better. The ability to directly probe spatially distributed electrons in materials opens up new opportunities to exploit real-space charge distributions, e.g., anionic electrons in electrides, the local charge redistribution caused by Moiré superlattices in bilayer 2D materials (46, 47), or the 2D electron gas that forms at some oxide interfaces (48, 49), to tailor these exciting materials for energy and quantum applications.
MATERIALS AND METHODS
Bulk sample preparation
Polycrystalline Y5Si3 sample was prepared by directly arc-melting high-purity yttrium (99.99% pure; AMES) and Si (99.9999% pure; Alfa Aesar) elements with a molar ratio of 5:3 (9). Before melting, the arc-melter chamber was evacuated and back-filled with Ar for a few times. Zr was used as an oxygen getter and melted before Y and Si were arc-melted. The melted button was flipped over and remelted for five times to create a homogeneous sample. The weight loss during arc-melting was less than 0.1 mass %. The obtained ingot is extremely stable under air and also water durable (9). Nevertheless, after arc-melting, the ingot was transferred immediately into a He-filled glovebox for grinding and TEM specimen preparation.
X-ray diffraction
Room temperature powder x-ray diffraction pattern was recorded on a PANalytical X’pert Pro MPD powder diffractometer using Cu Kα1 radiation. Powder data were analyzed using the WinCSD program package (50).
STEM data acquisition
All the STEM data were acquired on a dedicated aberration-corrected Nion UltraSTEM100 equipped with a cold field-emission electron source, operated at an accelerating voltage of 100 kV. The probe is ~20 pA with a convergence semi-angle of 30 mrad. HAADF-STEM images were collected using the ~86 to 200 mrad semi-angle range.
DPC imaging was performed on a Nion 2020 Ronchigram camera, with a Hamamatsu ORCA ultra-low noise scientific CMOS sensor and a 2048 × 2048 pixel display. This camera can operate at a rate of 400 megapixels/second, with a readout noise of 1.6 well e− (root mean square). The display readout capability for this camera is between dedicated pixelated detectors and direct electron detectors (33). The full detector is cropped to read out a 48 × 48 pixel region for each Ronchigram. The acquisition time for all dataset in this work was 1 ms per Ronchigram image. The camera length of the microscope was adjusted to produce a diffraction plane calibration of 2.5 mrad per pixel.
DPC works by correlating the momentum transfer into the beam with the electric field experienced by the beam electrons. By using the pixelated detector, we can accurately measure the CoM of the CBED pattern, which, for extremely thin samples, corresponds to the momentum transfer because of the projected electric field in the material. Here, we use the thinnest observable regions in the electride for our DPC analysis, and these areas are still thick for direct quantitative analysis for atomic columns of heavy elements but provide a strong qualitative match to theory for anionic electron columns (more details in later sections). By equating the direction and magnitude of the CoM shifts to the electric field, we can take the divergence of the electric field to find the crystal charge density through Gauss’s law. The HAADF images were recorded simultaneously to the DPC datasets.
DFT calculations
DFT calculations based on pseudopotentials were performed using the VASP package (51). All-electron DFT calculations were performed using ELK (52). We used the projector augmented wave (53) pseudopotential method and the Perdew-Burke-Ehrenhof (PBE) (54) generalized gradient approximation (GGA) for exchange and correlation. The GGA-PBE pseudopotentials are found to produce more accurate lattice constants than the local density approximation as shown in table S1. The unit cell was relaxed with a convergence of 10−8 eV for the total energy and 10−5 eV/Å for the forces on each atom. The plane-wave energy cutoff is 500 eV. The electronic k-space integration was performed with the tetrahedron method, involving a Γ-centered 12 × 12 × 16 k-mesh. In the DFT calculations, the unit cell is divided into a 128 × 128 × 6 mesh for the charge density, electrostatic potential, and electric field. We also performed calculations using a 2 × 2 × 1 supercell. The resulting charge density, electric field, etc. are the same as using unit cell.
HAADF and PACBED simulations
The HAADF image and PACBED simulations were performed using the frozen phonon model with a 100-kV probe with a probe-forming aperture semi-angle of 30 mrad via μSTEM code (55). A supercell of 67.2 Å × 72.7 Å viewed along the [110] orientation comprising 256 × 256 pixels was used. By comparing experimental PACBED with the simulations, we determined that the experimental specimen thickness is 7 unit cells (= 44.1 Å) (fig. S3). The experimental defocus was set in the middle of the specimen thickness, and therefore, we used C1 = 22 Å in the simulation.
INS spectroscopy
The INS spectrum of the sample was measured at the VISION beam line at the Spallation Neutron Source (Oak Ridge National Laboratory), an accelerator-based pulsed neutron source operating at 1.4-MW proton beam power. VISION is an inverted geometry spectrometer for neutron energy loss vibrational spectroscopy. It measures incident neutron energy by time of flight. The final neutron energy (3.5 meV) is set by a series of curved pyrolytic graphite mirrors. The dynamic range is from 0 to 8000 cm−1 with a nearly uniform resolution of 1 to 1.5% across this dynamic range. The sample was then cooled to 5 K in a top-loading, closed-cycle refrigerator at the beam line and measured for ~10 hours. The spectrum of the empty sample holder was subtracted to obtain the signal from the sample. INS quantification is performed by using 0.5H-Y5Si3 as a reference and calculating the relative intensity of scattering by H versus that by the bulk crystal (energy transfer region, 20 to 300 cm−1).
Acknowledgments
M.C. gratefully acknowledges the valuable discussions and support from H. Hosono and his colleagues at the Tokyo Institute of Technology. Funding: The microscopy work was supported by an Early Career project supported by DOE Office of Science FWP #ERKCZ55–KC040304. All microscopy technique development was performed and supported by Oak Ridge National Laboratory’s (ORNL) Center for Nanophase Materials Sciences (CNMS), which is a DOE Office of Science User Facility. Q.Z., J.Y., and B.C.S. were supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), Materials Sciences and Engineering Division. Q.Z. thanks the partial support by the NSF-MRSEC. Theoretical work by T.F. and S.T.P. was supported, in part, by DOE grant DE-FG0209ER46554 and by the McMinn Endowment. Y.I., N.S., and R.I. were supported by the Nanotechnology Platform (project no.12024046) from MEXT, Japan, JST-SENTAN, and JST-PRESTO, respectively. The computations partially used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility funded through contract no. DE-AC02-05CH11231, and partially used the Extreme Science and Engineering Discovery Environment (XSEDE). The neutron scattering experiment was performed at ORNL’s Spallation Neutron Source, supported by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. DOE, under contract no. DE-AC0500OR22725 with UT Battelle, LLC. Author contributions: M.C. and Q.Z. conceived the project. Q.Z., J.Y., J.X., and B.C.S. synthesized the sample. Q.Z. and J.A.H. acquired the experimental data. T.F. and S.T.P. performed the DFT calculations. J.A.H. performed the experimental data analysis. R.I. performed image simulations. J.C.I. did initial image simulations. Q.Z., T.F., J.A.H., M.C., and S.T.P. prepared the manuscript. Y.C. and L.D. performed neutron scattering experiments. All authors were involved in the interpretation of data and the writing of the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/15/eabe6819/DC1
REFERENCES AND NOTES
- 1.Dawes S. B., Ward D. L., Huang R. H., Dye J. L., First electride crystal structure. J. Am. Chem. Soc. 108, 3534–3535 (1986). [Google Scholar]
- 2.Huang R. H., Faber M. K., Moeggenborg K. J., Ward D. L., Dye J. L., Structure of K+(cryptand[2.2.2J]) electride and evidence for trapped electron pairs. Nature 331, 599–601 (1988). [Google Scholar]
- 3.Dye J. L., Electrides: Ionic salts with electrons as the anions. Science 247, 663–668 (1990). [DOI] [PubMed] [Google Scholar]
- 4.Singh D. J., Krakauer H., Haas C., Pickett W. E., Theoretical determination that electrons act as anions in the electride Cs+ (15-crown-5)2·e. Nature 365, 39–42 (1993). [Google Scholar]
- 5.Wagner M. J., Huang R. H., Eglin J. L., Dye J. L., An electride with a large six-electron ring. Nature 368, 726–729 (1994). [Google Scholar]
- 6.Matsuishi S., Toda Y., Miyakawa M., Hayashi K., Kamiya T., Hirano M., Tanaka I., Hosono H., High-density electron anions in a nanoporous single crystal: [Ca24Al28O64]4+·4e−. Science 301, 626–629 (2003). [DOI] [PubMed] [Google Scholar]
- 7.Lee K., Kim S. W., Toda Y., Matsuishi S., Hosono H., Dicalcium nitride as a two-dimensional electride with an anionic electron layer. Nature 494, 336–340 (2013). [DOI] [PubMed] [Google Scholar]
- 8.Park J., Lee K., Lee S. Y., Nandadasa C. N., Kim S., Lee K. H., Lee Y. H., Hosono H., Kim S.-G., Kim S. W., Strong localization of anionic electrons at interlayer for electrical and magnetic anisotropy in two-dimensional Y2C electride. J. Am. Chem. Soc. 139, 615–618 (2017). [DOI] [PubMed] [Google Scholar]
- 9.Lu Y., Li J., Tada T., Toda Y., Ueda S., Yokoyama T., Kitano M., Hosono H., Water durable electride Y5Si3: Electronic structure and catalytic activity for ammonia synthesis. J. Am. Chem. Soc. 138, 3970–3973 (2016). [DOI] [PubMed] [Google Scholar]
- 10.Zhang Y., Xiao Z., Kamiya T., Hosono H., Electron confinement in channel spaces for one-dimensional electride. J. Phys. Chem. Lett. 6, 4966–4971 (2015). [DOI] [PubMed] [Google Scholar]
- 11.Zhang Y., Wang H., Wang Y., Zhang L., Ma Y., Computer-assisted inverse design of inorganic electrides. Phys. Rev. X 7, 011017 (2017). [Google Scholar]
- 12.Park C., Kim S. W., Yoon M., First-principles prediction of new electrides with nontrivial band topology based on one-dimensional building blocks. Phys. Rev. Lett. 120, 026401 (2018). [DOI] [PubMed] [Google Scholar]
- 13.Hirayama M., Matsuishi S., Hosono H., Murakami S., Electrides as a new platform of topological materials. Phys. Rev. X 8, 031067 (2018). [Google Scholar]
- 14.Kitano M., Inoue Y., Yamazaki Y., Hayashi F., Kanbara S., Matsuishi S., Yokoyama T., Kim S.-W., Hara M., Hosono H., Ammonia synthesis using a stable electride as an electron donor and reversible hydrogen store. Nat. Chem. 4, 934–940 (2012). [DOI] [PubMed] [Google Scholar]
- 15.Kitano M., Kanbara S., Inoue Y., Kuganathan N., Sushko P. V., Yokoyama T., Hara M., Hosono H., Electride support boosts nitrogen dissociation over ruthenium catalyst and shifts the bottleneck in ammonia synthesis. Nat. Commun. 6, 6731 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Miyakawa M., Kim S. W., Hirano M., Kohama Y., Kawaji H., Atake T., Ikegami H., Kono K., Hosono H., Superconductivity in an inorganic electride 12CaO·7Al2O3:e−. J. Am. Chem. Soc. 129, 7270–7271 (2007). [DOI] [PubMed] [Google Scholar]
- 17.Zhang Y., Wang B., Xiao Z., Lu Y., Kamiya T., Uwatoko Y., Kageyama H., Hosono H., Electride and superconductivity behaviors in Mn5Si3-type intermetallics. npj Quantum Mater. 2, 45 (2017). [Google Scholar]
- 18.Lu Y., Wang J., Li J., Wu J., Kanno S., Tada T., Hosono H., Realization of Mott-insulating electrides in dimorphic Yb5Sb3. Phys. Rev. B 98, 125128 (2018). [Google Scholar]
- 19.Kim S. W., Shimoyama T., Hosono H., Solvated electrons in high-temperature melts and glasses of the room-temperature stable electride [Ca24Al28O64]4+·4e−. Science 333, 71–74 (2011). [DOI] [PubMed] [Google Scholar]
- 20.McColm I. J., Kotrocvo V., Button T. W., Clark N. J., Bruer B., Hydrogen sorption properties of D88-type systems: I. Hydrides of Y5Si3. J. Less Common Met. 115, 113–125 (1986). [Google Scholar]
- 21.McColm I. J., Ward J. M., Hydrogen sorption properties of D88-type systems: IV. Y5Ge3 and Y5Si3-Y5Ge3 solid solutions. J. Alloys Compd. 178, 91–100 (1992). [Google Scholar]
- 22.Zhang X., Xiao Z., Lei H., Toda Y., Matsuishi S., Kamiya T., Ueda S., Hosono H., Two-dimensional transition-metal electride Y2C. Chem. Mater. 26, 6638–6643 (2014). [Google Scholar]
- 23.Inoshita T., Jeong S., Hamada N., Hosono H., Exploration for two-dimensional electrides via database screening and Ab Initio Calculation. Phys. Rev. X 4, 031023 (2014). [Google Scholar]
- 24.Jing Y., Ma Y., Li Y., Heine T., GeP3: A small indirect band Gap 2D crystal with high carrier mobility and strong interlayer quantum confinement. Nano Lett. 17, 1833–1838 (2017). [DOI] [PubMed] [Google Scholar]
- 25.Rojac T., Bencan A., Drazic G., Sakamoto N., Ursic H., Jancar B., Tavcar G., Makarovic M., Walker J., Malic B., Damjanovic D., Domain-wall conduction in ferroelectric BiFeO3 controlled by accumulation of charged defects. Nat. Mater. 16, 322–327 (2017). [DOI] [PubMed] [Google Scholar]
- 26.Han Y., Li M.-Y., Jung G.-S., Marsalis M. A., Qin Z., Buehler M. J., Li L.-J., Muller D. A., Sub-nanometre channels embedded in two-dimensional materials. Nat. Mater. 17, 129–133 (2017). [DOI] [PubMed] [Google Scholar]
- 27.Krivanek O. L., Chisholm M. F., Nicolosi V., Pennycook T. J., Corbin G. J., Dellby N., Murfitt M. F., Own C. S., Szilagyi Z. S., Oxley M. P., Pantelides S. T., Pennycook S. J., Atom-by-atom structural and chemical analysis by annular dark-field electron microscopy. Nature 464, 571–574 (2010). [DOI] [PubMed] [Google Scholar]
- 28.Song K., Ryu S., Lee H., Paudel T. R., Koch C. T., Park B., Lee J. K., Choi S.-Y., Kim Y.-M., Kim J. C., Jeong H. Y., Rzchowski M. S., Tsymbal E. Y., Eom C.-B., Oh S. H., Direct imaging of the electron liquid at oxide interfaces. Nat. Nanotechnol. 13, 198–203 (2018). [DOI] [PubMed] [Google Scholar]
- 29.Lee H., Campbell N., Lee J., Asel T. J., Paudel T. R., Zhou H., Lee J. W., Noesges B., Seo J., Park B., Brillson L. J., Oh S. H., Tsymbal E. Y., Rzchowski M. S., Eom C. B., Direct observation of a two-dimensional hole gas at oxide interfaces. Nat. Mater. 17, 231–236 (2018). [DOI] [PubMed] [Google Scholar]
- 30.Shibata N., Findlay S. D., Kohno Y., Sawada H., Kondo Y., Ikuhara Y., Differential phase-contrast microscopy at atomic resolution. Nat. Phys. 8, 611–615 (2012). [Google Scholar]
- 31.Shibata N., Seki T., Sánchez-Santolino G., Findlay S. D., Kohno Y., Matsumoto T., Ishikawa R., Ikuhara Y., Electric field imaging of single atoms. Nat. Commun. 8, 15631 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ishikawa R., Findlay S. D., Seki T., Sánchez-Santolino G., Kohno Y., Ikuhara Y., Shibata N., Direct electric field imaging of graphene defects. Nat. Commun. 9, 3878 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hachtel J. A., Idrobo J. C., Chi M., Sub-Ångstrom electric field measurements on a universal detector in a scanning transmission electron microscope. Adv. Struct. Chem. Imaging 4, 10 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fang S., Wen Y., Allen C. S., Ophus C., Han G. G. D., Kirkland A. I., Kaxiras E., Warner J. H., Atomic electrostatic maps of 1D channels in 2D semiconductors using 4D scanning transmission electron microscopy. Nat. Commun. 10, 1127 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Müller K., Krause F. F., Béché A., Schowalter M., Galioit V., Löffler S., Verbeeck J., Zweck J., Schattschneider P., Rosenauer A., Atomic electric fields revealed by a quantum mechanical approach to electron picodiffraction. Nat. Commun. 5, 5653 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gao W. P., Addiego C., Wang H., Yan X., Hou Y., Ji D., Heikes C., Zhang Y., Li L., Huyan H., Blum T., Aoki T., Nie Y., Schlom D. G., Wu R., Pan X., Real-space charge-density imaging with sub-ångström resolution by four-dimensional electron microscopy. Nature 575, 480–484 (2019). [DOI] [PubMed] [Google Scholar]
- 37.Lv B., Zhu X. Y., Lorenz B., Wei F. Y., Xue Y. Y., Yin Z. P., Kotliar G., Chu C. W., Superconductivity in the Mn5Si3-type Zr5Sb3 system. Phys. Rev. B 88, 134520 (2013). [Google Scholar]
- 38.Müller-Caspary K., Krause F. F., Grieb T., Löffler S., Schowalter M., Béché A., Galioit V., Marquardt D., Zweck J., Schattschneider P., Verbeeck J., Rosenauer A., Measurement of atomic electric fields and charge densities from average momentum transfers using scanning transmission electron microscopy. Ultramicroscopy 178, 62–80 (2017). [DOI] [PubMed] [Google Scholar]
- 39.Sánchez-Santolino G., Lugg N. R., Seki T., Ishikawa R., Findlay S. D., Kohno Y., Kanitani Y., Tanaka S., Tomiya S., Ikuhara Y., Shibata N., Probing the internal atomic charge density distributions in real space. ACS Nano 12, 8875–8881 (2018). [DOI] [PubMed] [Google Scholar]
- 40.Ehrenfest P., Bemerkung über die angenäherte Gültigkeit der klassischen Mechanik innerhalb der Quantenmechanik. Z. Phys. 45, 455–457 (1927). [Google Scholar]
- 41.Lubk A., Zweck J., Differential phase contrast: An integral perspective. Phys. Rev. A 91, 023805 (2015). [Google Scholar]
- 42.Cao M. C., Han Y. M., Chen Z., Jiang Y., Nguyen K. X., Turgut E., Fuchs G. D., Muller D. A., Theory and practice of electron diffraction from single atoms and extended objects using an EMPAD. Microscopy 67, i150–i161 (2018). [DOI] [PubMed] [Google Scholar]
- 43.Togo A., Tanaka I., First principles phonon calculations in materials science. Scripta Mater. 108, 1–5 (2015). [Google Scholar]
- 44.Cheng Y. Q., Daemen L. L., Kolesnikov A. I., Ramirez-Cuesta A. J., Simulation of inelastic neutron scattering spectra using OCLIMAX. J. Chem. Theory Comput. 15, 1974–1982 (2019). [DOI] [PubMed] [Google Scholar]
- 45.Hood Z. D., Cheng Y. Q., Evans S. F., Adhikari S. P., Paranthaman M. P., Unraveling the structural properties and dynamics of sulfonated solid acid carbon catalysts with neutron vibrational spectroscopy. Catal. Today 358, 387–393 (2020). [Google Scholar]
- 46.Regan E. C., Wang D., Jin C., Utama M. I. B., Gao B., Wei X., Zhao S., Zhao W., Zhang Z., Yumigeta K., Blei M., Carlström J. D., Watanabe K., Taniguchi T., Tongay S., Crommie M., Zettl A., Wang F., Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020). [DOI] [PubMed] [Google Scholar]
- 47.Jiang Y. H., Lai X. Y., Watanabe K., Taniguchi T., Haule K., Mao J. H., Andrei E. Y., Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91–95 (2019). [DOI] [PubMed] [Google Scholar]
- 48.Ohtomo A., Hwang H. Y., A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004). [DOI] [PubMed] [Google Scholar]
- 49.Gariglio S., Reyren N., Caviglia A. D., Triscone J.-M., Superconductivity at the LaAlO3/SrTiO3 interface. J. Phys. Condens. Matter 21, 164213 (2009). [DOI] [PubMed] [Google Scholar]
- 50.Akselrud L., Grin Y., WinCSD: Software package for crystallographic calculations (Version 4). J. Appl. Cryst. 47, 803–805 (2014). [Google Scholar]
- 51.Kresse G., Hafner J., Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993). [DOI] [PubMed] [Google Scholar]
- 52.The Elk Code; http://elk.sourceforge.net/.
- 53.Blöchl P. E., Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
- 54.Perdew J. P., Burke K., Ernzerhof M., Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
- 55.Allen L. J., D’Alfonso A. J., Findlay S. D., Modelling the inelastic scattering of fast electrons. Ultramicroscopy 151, 11–22 (2015). [DOI] [PubMed] [Google Scholar]
- 56.Parthé E., The crystal structure of Y5Si3 and Y5Ge3. Acta Crystallogr. 13, 868–871 (1960). [Google Scholar]
- 57.Zhang H.-R., Egerton R. F., Malac M., Local thickness measurement through scattering contrast and electron energy-loss spectroscopy. Micron 43, 8–15 (2012). [DOI] [PubMed] [Google Scholar]
- 58.Roger J., Ben Yahia M., Babizhetskyy V., Bauer J., Cordier S., Guérin R., Hiebl K., Rocquefelte X., Saillard J. Y., Halet J. F., Mn5Si3-type host-interstitial boron rare-earth metal silicide compounds RE5Si3: Crystal structures, physical properties and theoretical considerations. J. Solid State Chem. 179, 2310–2328 (2006). [Google Scholar]
- 59.Mayer I., Shidlovsky I., M5X3-type rare earth silicides and germanides and their ternary phases with carbon. Inorg. Chem. 8, 1240–1243 (1969). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/15/eabe6819/DC1


