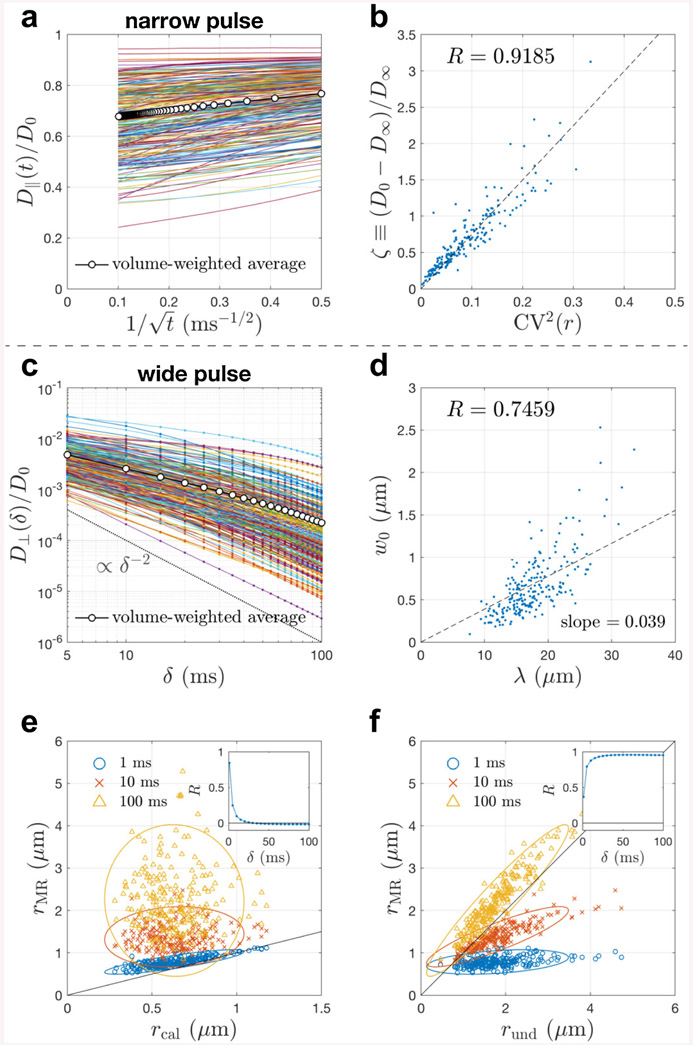
Fig. 3. Simulated apparent diffusivity parallel and transverse to 227 realistic axons segmented from a mouse brain corpus callosum.

a-b In the narrow pulse limit, the simulated time(t)-dependent diffusivity D_∥(t) along axons scales as $1∕\sqrt{t}$ in Eq. (8), and its bulk diffusivity D_∞ correlates with the caliber variation CV(r) via Eq. (9). c In the wide pulse limit (t = δ), the simulated diffusivity D_⊥(δ) transverse to axons scales as δ⁻² (dashed line) at very long times δ ≳ 50 ms. d Based on the analysis of realistic axonal skeleton (Appendix D), the estimated undulation wavelength λ positively correlates with the undulation amplitude w₀. e-f Translating the simulated D_⊥ into an effective radius r_MR measured by MR via Eq. (10), the value of r_MR is compared with the contributions of caliber variations and undulations, r_cal and r_und in Eq. (11) respectively. The Pearson’s correlation coefficient R of r_MR and each contribution is also shown as a function of time δ (insets). The result in panel b is similar to Fig. 2d in (Lee et al., 2020b), whereas the short T₂ and slow diffusivity in mitochondria are ignored here to focus on the effect of axonal shape. The results in panels c and e-f are similar, but not identical, to the ones obtained using ERL algorithm in Fig. 7 of (Lee et al., 2020a). Here, these simulations were re-done using elastic collision with impermeable membranes, and the estimation of undulation amplitude and wavelength is purely based on the geometry of axonal skeleton, as opposed to using ERL in simulations and fitting a 1-harmonic undulation model to simulated D_⊥ with fit parameters w₀ and λ in (Lee et al., 2020a). The effective theory parameters and scaling relations are essentially the same for both MC implementations (elastic collision vs ERL) because only diffusion simulations within impermeable cells were performed.