Differences Between Young and Older Adults in Unity and Diversity of Executive Functions

Abstract

In an influential study of young adults in 2000, Miyake and colleagues identified three independent components of executive function—set shifting, inhibition of prepotent responses, and updating and monitoring of working memory—which, although separable in a confirmatory factor analysis, were moderately correlated. Since that time, only a few studies have tried to replicate this factor structure in older adults, with inconsistent findings. The goals of the present study were to use the same executive function tests in young adults (ages 18-32) and two groups of older adults (ages 60-73 and 74-98), and compare the factor structure across groups. A full three-factor model of shifting, inhibition and updating was confirmed in young adults, but unlike Miyake’s finding, the factors were uncorrelated or weakly correlated. In both older groups, a two-factor solution was indicated, with tests of updating and inhibition associated with one factor and tests of shifting representing the other factor. In the young-older group, the two factors were moderately correlated (.30) and in the old-older group, they were strongly correlated (.53). A nested factors model of the data in the old-older group indicated that a common factor loaded on all but one of the tests and accounted for all of the variance in updating and inhibition. Only shifting retained factor-specific variance. We concluded that in young adulthood, shifting, updating, and inhibition may operate relatively independently. As people age, however, and processing becomes less efficient, they may rely increasingly on general executive control processes, reallocating their limited resources to optimize performance.

The study of executive function has increased dramatically in recent years as researchers, theorists, and clinicians have tried to capture both the essence of executive function in general terms and its component processes more specifically. Although there is still not complete agreement, there is at least some consensus that executive function involves broad-based attentional control or self-regulation of goal-relevant behaviors across a variety of tasks and domains. Such control may be subserved by a host of more specific cognitive processes that can be called upon in different contexts or to attain different goals. Although these cognitive/executive processes have been shown to be associated with different regions of prefrontal cortex both in functional neuroimaging (e.g., Braver, Reynolds, & Donaldson, 2003; D’Esposito, Postle, Ballard, & Lease, 1999; D’Esposito, Postle, & Rypma, 2000; Turner & Spreng, 2012) and patient studies (e.g., Shallice, Stuss, Alexander, Picton & Derkzen, 2008; Stuss, 2011), the exact nature of these processes and their neural correlates remains uncertain. Many of the neuropsychological tests that are often used to measure executive function such as the Wisconsin Card Sorting Test and the Tower of Hanoi are complex tasks, involving multiple cognitive processes, executive and non-executive, and several brain regions, making it difficult to ascertain exactly what specific aspects of executive function may be contributing to performance (see Banich, 2009).

Historically, executive function tasks were designed to assess cognitive disabilities in patients with prefrontal damage. In this context, it became evident that these patients had a variety of symptoms, the constellation of which differed across individuals but suggested a common lack of executive or attentional control (Shallice, 1982). This clinical presentation came to be known as the “dysexecutive syndrome” (Baddeley, 1986; Baddeley & Wilson, 1988). More recently, these neuropsychological tests have been used to explore individual differences in healthy older adults and their relation to age-related declines in the brain, particularly in the frontal lobes, a region particularly sensitive to aging (e.g., Hedden, 2007; Raz, 2005). Several studies have reported that performance on executive function tasks, which tends to decline with age, correlates with frontal brain volumes in older adults (e.g., Gunning-Dixon & Raz, 2003). Findings, however, have not been entirely consistent (for review, see Yuan & Raz, 2014) and additional posterior brain regions, particularly the parietal lobes, have also been implicated (e.g., Collette et al., 2005; Manard, Bahri, Salmon, & Collette, 2016; Sylvester et al., 2003). Integrity of frontal-parietal white matter tracts has also been linked to executive function (e.g., Bettcher et al., 2016; Smolker, Friedman, Hewitt, & Banich, 2018). Differences in outcomes across studies are likely attributable to differences in the tasks used, but as yet, the specific cognitive processes associated with each task and their neural correlates have not been reliably identified, although progress has been made (for discussion, see Stuss & Craik, 2020). Understanding the component sub-processes of these complex executive function tasks clearly continues to be an important goal, not only theoretically but also clinically, so that neuropsychologists and geropsychologists can assess cognitive deficits more precisely and design more targeted interventions.

In the cognitive aging domain, there have been only a few attempts to characterize potential sub-components of executive function, most of which have used some form of factor analysis and structural equation modeling (for review, see Karr et al., 2018). Several of these studies were modeled after an influential study by Miyake and colleagues (2000) in young adults in which they identified three basic and separable factors of executive function: set shifting, inhibition of prepotent responses, and updating and monitoring of working memory, with three tasks associated with each factor. The factors were also differentially predictive of performance on complex executive function tasks, further supporting the view that they represented independent processes. However, although they each captured differentiated components of executive function, the three factors were also moderately correlated with each other (.42-.63) suggesting some common variance among them. These findings formed the basis of what has become known as the unity and diversity model of executive function (e.g., Friedman & Miyake, 2017; Smolker et al., 2018), which proposes that although there exist separable sub-components of executive function, they nevertheless share a common process that unifies them.

Attempts to replicate this factor structure in older adults have produced mixed findings. A study by Hedden and Yoon (2006) with a group of 129 older adults aged 63-82, used tests of executive function similar to those used by Miyake et al. (2000), along with tests of memory and processing speed. They reported that for the executive function tests, the model of best fit included just two correlated factors—shifting/updating and resistance to proactive interference—while the Stroop test, a putative measure of inhibition, loaded weakly with a speed factor. On the other hand, Hull and colleagues (Hull, Martin, Beier, Lane, & Hamilton, 2008), in a confirmatory factor analysis (CFA) of the Miyake et al. model in 100 older adults aged 51-74, initially found a similar three-factor solution but the factors were not correlated. Subsequently, the Inhibition factor was dropped because there was only one significant indicator (the verbal Stroop). In the surviving two-factor model, one of the tests (plus-minus), which was related to Shifting in young people (in Miyake et al.), loaded with Updating in the older adult sample. Hull et al. concluded that a two-independent factor model featuring Shifting and Updating best described the data, and that the relative contributions of the underlying processes were different in older people, with updating playing an increasingly important role. However, Vaughan & Giovanello (2010) replicated the CFA results of Miyake et al. in a group of 95 older adults (aged 60-90), finding three correlated factors of Shifting, Updating, and Inhibition, although the correlations appeared to be somewhat stronger (.63-.81) than those reported by Miyake for young people. Finally, a study by Bettcher et al. (2016) in older adults (aged 63-99) reported a two-factor (Shifting/Inhibition and Updating/Working Memory) plus speed model, in which the two executive function factors were correlated with each other and both were correlated with speed. Inhibition in this study was highly correlated with Shifting (.97), and so was subsumed under the Shifting variable (see also Frazier et al., 2015).

Although each of these studies provided a test of the Miyake et al. (2000) three-factor model of executive function in older adults, the specific tests and measures chosen to represent each of the hypothesized factors were different across studies, and may have accounted for the different outcomes. In addition, none of the experiments included a group of younger adults for a direct comparison of the identical set of tests in the two age groups. Further, the older age groups ranged from 51 to 99 years of age and spanned 19 to 36 years. So although all of the findings are consistent with the view that executive control depends on a variety of underlying cognitive processes, the extent to which the factor structure is invariant or changes across age remains unclear. There has also been at least one age-heterogeneous study (ages 18-81, N=95), using an exploratory principal components analysis of complex executive function tasks (Fisk & Sharpe, 2004), in which four uncorrelated factors were found. Three of them appeared to reflect the Miyake et al. components, and an additional fourth factor emerged, based on verbal fluency, which they labeled long-term memory access. Although findings were consistent with the view that there are multiple and separable executive function processes that decline with age, this study did not permit any conclusions with respect to whether the factor structure was the same in older and younger people.

Since their original paper in 2000, Miyake, Friedman, and colleagues have further confirmed the three-correlated factor structure in young adults (e.g., Friedman et al., 2006), and have developed another model with an additional factor to account for the shared variance among the three factors (Friedman et al,, 2008). They refer to this as a Common Executive Function (EF) factor, because it represents the variance common to all of the individual executive function tests. This more recent model also included two nested factors, Updating and Shifting, which accounted for variance that was specific to those two abilities. A separate Inhibition factor was no longer indicated, however, since its variance was entirely captured by the Common EF factor. This model, now referred to as a bi-factor or nested factors model, has formed the basis for much of the continuing research of Friedman, Miyake and colleagues, providing what they consider to be a more direct and informative account of the unity and diversity of executive functions. Although to our knowledge the nested- factors model has not been demonstrated in older adults, a recent study by Gustavson et al. (2018) revealed a similar bi-factor model in a group of middle-aged adults (aged 51-60) in which all seven of the executive function tasks loaded to the Common EF factor, accounting for all of the variance in the inhibition and shifting tasks, along with a single Working Memory-specific factor.

The immediate goals of the present study were a) to test and compare younger and older adults on the same set of executive function tests, b) to confirm the basic three-factor structure obtained by Miyake et al. (2000) and Friedman et al. (2008) in young adults, c) to test whether the same or a different factor structure would emerge with age, and d) to test whether a nested factors model could be identified. Based on the inconsistent findings in older adults and the likelihood of considerable heterogeneity across the range of years often included in older groups (e.g., 60-90), we decided to include both a young-older group and an old-older group to gain additional information about possible changes in executive functioning during late-life aging. To our knowledge, only one study has looked at young-older and old-older groups separately in a factor analytic paradigm. De Frias, Dixon and Strauss (2006) found that a single factor accounted for performance across four tests in older adults, two that reflected shifting and two that required inhibition, and the structure was invariant across 53-70-year olds and 71-90-year olds. Three of the four tests used in this study, however, were different from those used in the original Miyake et al. study, once again illustrating the difficulty in making comparisons across studies.

The longer-term goal of the present study was to gain further understanding of the cognitive processes underlying the construct of executive function so as to establish a manageable executive function battery for older adults that would include specific measures of some of the those fundamental processes. To accomplish these goals, we selected a subset of the tests used by Miyake et al. (2000), administered them to young adults and two groups of older adults, and conducted several CFAs, initially comparing groups directly on the full three-factor model, and following up with tests of one- and two-factor models, and the nested-factor model where appropriate.

Method

Participants

Three groups participated in the study: 124 young adults (aged 18-32, M = 21.5, SD = 3.2), 120 healthy, young-older adults (aged 60-73, M = 68.0., SD = 3.5), and 125 old-older adults (aged 74-98, M = 79.6, SD = 4.8). They were selected from the three laboratories of the principal investigators (ELG, GEA, LR). All older adults were normally-aging, healthy, community-dwelling volunteers without dementia (MMSE = 29, range = 25-30), depression, prior history of neurological or psychiatric problems, or substance abuse. The older adults were divided into two age groups based on an approximate median split (median = 73.9). There were 72 women and 48 men in the young-older group, and 82 women and 43 men in the old-older group, with an average of 17 years of education in both groups (SDs = 2.2, 2.6). Young people were undergraduates in psychology courses at the University of Arizona who participated for course credit. There were 58 women and 66 men with an average of 14.3 years of education (SD = 1.8). The older adults had significantly more years of education than the young, ps < .001. The sex distribution was significantly different across age groups, χ² (2, N = 369) = 9.50, p = .009. Follow-up comparisons indicated that the young adults differed significantly from the young-older adults, χ² (1, N = 244) = 4.29, p = .038 and the old-older adults, χ² (1, N = 249) = 8.96, p = .003, but the two older groups did not differ from each other, χ² (1, N = 245) = .82, p = .364. All consenting and other procedures were approved by the University of Arizona’s Human Subjects Protection Program.

Tasks

Two tests were selected to represent each of the three executive function factors: shifting, updating, and inhibition. Five of the six tests were the same as those used by Miyake et al. (2000) with some modifications in the measures as noted below. They represent a subset of the nine tests (three per factor) previously described in Miyake et al. and in Alexander et al. (2012). These tasks were selected because they had shown consistent loadings to the hypothesized latent factors across studies, and had previously been shown to be age-sensitive. The Simon task, which was not included in Miyake et al., served as one of our tests of inhibition. All of the tests except the Stroop were programmed in E-prime and administered by computer.

Shifting

a). Number-letter.

In this task (adapted from Rogers & Monsell, 1995), a number-letter pair (e.g., 7F) was presented in one of four quadrants on the computer screen. If the stimulus pair occurred in one of the top two quadrants, participants were to judge whether the number was odd or even. If it occurred in the bottom two quadrants, participants judged whether the letter was a consonant or vowel. In the first block of 32 trials, the stimulus appeared only on the top half of the screen; in the second block of 32 trials, it appeared only on the bottom; and in the third block of 64 trials (the shift block), it moved in a clockwise fashion across trials starting in the top left, so that the same task was repeated on half of the trials and shifted on the other half in a predictable pattern. Responses were made by key press (odd/even on the “1” and “2” keys of the keypad with the right hand, and consonant/vowel on “c” and “v” keys with the left hand). There was a 150 ms inter-trial interval (ITI). Each block of trials was preceded by several practice trials—10 in the no-shift blocks, and 12 in the shift block. The dependent measure was the global-shift cost: the difference between the average RTs for the shift block and the average RTs across the two no-shift blocks. To control for differences in baseline speed of responding, we used a proportional measure, dividing the difference scores by the average RTs for the no-shift blocks.

b). Global-local.

In this task, participants viewed geometric figures on a computer screen, either a large square made up of smaller triangles, or a large triangle made up of smaller squares (Navon, 1977). If the figure was blue, people were to identify the global shape; if the figure was black they were to identify the local shapes. This rule was counterbalanced across participants. Half of the stimuli were blue, half were black, and half of each color were squares made up of triangles and half were triangles made up of squares. In the first block of 24 trials, all of the stimuli were the same color, in the second block of 24 trials all were the other color, and in the third block of 48 trials, stimuli of both colors were randomly mixed such that the task repeated on half of the trials and shifted on the other half, but there was no pattern to the shifting. Order of the first two blocks of trials was counterbalanced. Responses were mouse button presses (left for triangle and right for circle) followed by a 500 ms ITI. A minimum of 12 practice trials was given prior to each block, and feedback was provided to ensure at least 80% accuracy before the experimental trials began (in which there was no feedback). Here too, to control for differences in baseline response time, the dependent measure was the proportional global shift cost: the difference in RTs between the shift block and the average of the two no-shift blocks, relative to the no-shift blocks.

Miyake et al. (2000) used a mix of global and local shift costs (i.e., difference between repeated and non-repeated trials within a shift block) across their three tasks. In later studies, they measured only local shift costs in which switch and repeat trials occurred in a random order (e.g.,Friedman et al., 2008; Smolker et al., 2018). However, previous studies have indicated that the two kinds of shifts are dependent on different brain regions (e.g., Braver et al., 2003), and that whereas global shift costs show age-related differences, local shift costs generally do not (e.g., Gamboz, Borella, & Brandimonte, 2009; Verhaeghen & Cerella, 2008). These findings suggest that the two kinds of shifts involve different processes. Because we were ultimately interested in establishing an executive function battery for older adults, we chose to focus solely on the age-dependent global shift costs for both of our tasks.

Updating

a). Consonant updating/letter memory.

In this task (adapted from Morris & Jones, 1990), a continuous stream of individual consonants was presented in the middle of the computer screen. Participants had to repeatedly report the last four letters out loud, which required that they continuously update their working memory, adding each newly-presented letter and dropping out the 5^th letter back. At the end of the list, they repeated the last four letters. Letters were presented for 2 s with an inter-stimulus interval (ISI) of 1 s. The number of consonants in each list varied randomly with three lists of 5, 7, 9, and 11 letters. Practice included three 5-letter and three 7-letter sequences. The dependent measure was the proportion of correct letters reported in the correct order at the end of each list (out of a possible 48).

b). Keep track.

In this task (adapted from Yntema, 1963), participants were required to keep track of the last-presented instance of each of several categories. After first being familiarized with six categories (distances, fruits, furniture, metals, relatives, sports) and a list of six exemplars from each, twelve 15-item lists of words with 2-3 instances from each target category were presented one at a time in the center of the computer screen. Each word was shown for 1500 ms with a 150 ms ISI. Participants had to keep track of the last-presented instance of each of one, two, three, or four target categories. The names of the target categories for each trial appeared at the bottom of the screen and remained there throughout the trial. Three lists were presented for each category size, starting with one category and progressing up to four. The content of the lists and the order of presentation were fixed. The dependent measure was the proportion of correct responses (out of a possible 30). An example and a practice trial were also provided. In the Miyake et al. (2000) study, young participants were required to track four and five categories at a time. We used fewer categories to make the task more manageable for older adults. Friedman et al., (2008) used two to four categories with adolescents.

Inhibition

a). Stroop.

We used two lists from the Golden (1978) version of the Stroop (1935) task, which requires color-naming only; there was no task shifting involved. We compared the number of colors correctly named in 45 s when the stimuli were colored XXXXs (the neutral condition) to the number of colors correctly named when the stimuli were color names (blue, red, green) printed in incongruent colors (BLUE printed in red). Stimuli were presented on a single sheet (5 columns of 20) for each condition; errors were corrected. The inhibition measure reflects the difficulty that people experience inhibiting the prepotent response of reading the word in the incongruent condition compared to the neutral condition. We controlled for overall naming speed by using a proportional measure: the proportional decrease in the number of stimuli named in the incongruent condition relative to the neutral condition.

b). Simon.

In the Simon task (Simon, 1990; Castel, Balota, Hutchison, Logan, & Yap, 2007), people were required to press a key on the left side of the keyboard (Q) when a left-pointing arrow (←) appeared, and a key on the right side of the keyboard (P) when a right-pointing arrow (→) appeared. The arrows appeared on the computer screen on the left, middle or right, with 40 trials in each position. Half of the arrows in each position pointed right and half pointed left. Twelve practice trials were provided at the start, and feedback was provided throughout. The prepotent response is to press the key that is in the same spatial location as the stimulus. When the arrow appears on the left and is pointing right, the prepotent left-key response has to be inhibited and the right key pressed. The inhibition measure represented the proportional increase in RT when the direction of the arrow and its location were incongruent compared to when they were congruent.

We chose these two measures specifically because both of them have been characterized as reflecting inhibition of a prepotent response, but in different domains—Stroop in a verbal domain and Simon in a visuospatial domain. As mentioned above, inhibition has been a particularly difficult construct to pin down perhaps because it itself is not unitary. In earlier attempts to replicate Miyake et al.’s (2000) finding in older adults, neither Hedden & Yoon (2006) nor Hull et al. (2008) were able to identify inhibition per se as a latent variable (see also, Adrover-Roig, Sesé, Barceló, & Palmer, 2012). Friedman & Miyake (2004) found that inhibition could be broken down into at least 2 sub-components, one measuring resistance to proactive interference, and another dissociable component combining inhibition of prepotent responses and resistance to distractors. Others have suggested that there may be multiple kinds of inhibition, involving many different underlying cognitive mechanisms (e.g., Adrover-Roig, et al., 2012) differentially affected by aging (Collette, Germain, Hogge, & Van der Linden, 2009). In addition, Davidson & Glisky (2002; see also Rey-Mermet, Gade, & Oberauer, 2018) reported only very weak correlations among several tests thought to measure inhibitory control.

Procedure

The test battery was administered individually in the same way and with identical instructions to young and older adults across the three laboratories. The order of testing ensured that one test from each executive function category was tested before the second test from the same function was presented, and two tests from the same category did not appear consecutively. Eighteen young-older adults and thirty-eight old-older adults did not receive the Simon task. Approximately one hour was required to administer the complete battery.

Data Pre-processing

RT data, which were collected for three of the tests—number-letter, global-local and Simon—were pre-processed separately in each laboratory and then merged. Only correct responses were included. Any participants whose RTs for any condition were based on less than 50% of the trials were not included in the study. Fast responses (below 200 ms for the Simon and number-letter tasks, and below 300 ms for global-local) were considered to be errors (late responses for the preceding trial or anticipatory responses for the current trial) and were eliminated. The rest of the RT data were trimmed at the individual level for each condition separately. Responses that were more than 2.5 SDs above or below an individual’s mean RT for that condition were removed. These procedures resulted in a loss of less than 5% of the RT data.

Analyses

To enhance interpretation, scores submitted for analysis were adjusted so that higher numbers always represented better performance on all measures. Therefore, shifting and inhibition measures, which represent costs, will appear in Table 1 as negative numbers—the lower the number the worse the performance, whereas updating measures, which reflect proportion correct, will appear as positive numbers. The proportional shifting costs were logarithmically transformed prior to the CFAs to normalize the distributions.

A series of CFA models was planned to compare the factor structure in young, young-older and old-older age groups. First, to see whether the three groups shared the same general three-factor model structure that was reported by Miyake et al. (2000), we conducted a three-group CFA by testing a configural model. In this model, the three factors were allowed to correlate within each group and all parameters were freely estimated across groups. Subsequently, separate CFAs were performed on the data from each of the three age groups. We followed the same procedures as Miyake et al. (2000) and tested the fit of six models for each age group by comparing several different model specifications: (1) the full three-factor model, (2) a one-factor model, (3) three two-factor models, and (4) an independent three factor model. In all the specified models, each factor variance was fixed to 1.0 to set the scale of measurement. Factor loadings were set to be equal to each other for any factors with two indicators for the purpose of model identification, but were freely estimated for any factors with more than two indicators. We also planned to test two nested factors models to determine if a common EF factor could be identified (Freidman et al., 2008, 2011).

To evaluate the goodness of fit of each model, we considered several fit indices: (1) the chi-square value (χ²), (2) Akaike’s Information Criterion (AIC), (3) the standardized root mean squared residual (SRMR), (4) Bentler’s Comparative Fit Index (CFI), (5) Bollen’s Incremental Fit Index (IFI), and (6) the Root Mean Square Error of Approximation (RMSEA). Both χ² and AIC represent the extent to which the observed and predicted covariance matrices differ from each other. Lower AIC values and a nonsignificant χ² (Byrne, 1998) are generally considered indicators of a good fit of the observed data to the model. SRMR represents the square root of the averaged squared residuals, and values under .08 indicate good fit. CFI and IFI reflect the extent to which the tested model is better than a null model, in which all measured variables are assumed to be uncorrelated. CFI and IFI values from .90 to .95 indicate an acceptable fit, values higher than .95 indicate a close fit. RMSEA values below .05 indicate a good fit, and values from .05 to .08 indicate an acceptable fit (MacCallum & Austin, 2000; Hull et al., 2008). The best-fitting model among models that achieved an acceptable fit was determined by chi-squared difference tests (Δ χ²) and AIC values. For the nested models, χ² of the more restricted models (which have higher degrees of freedom) were subtracted from χ² of the more inclusive model (which has lower degrees of freedom). A statistically significant Δ χ² indicates that the more inclusive model is a significantly better fit, whereas a non-significant Δ χ² suggests that the restricted model is a significantly better fit. Alpha level was set at .05. AIC was used for comparisons of non-nested models.

All CFAs were conducted using PROC CALIS in SAS 9.4 (SAS Institute, 2013), using the maximum likelihood method to estimate the loadings of the specified latent variables as well as the correlations among them based on the observed covariance matrices. If none of the models had acceptable fit indices in any group,, we conducted an exploratory factor analysis (EFA) to identify the underlying factor structure in that group. The EFA was performed with PROC FACTOR in SAS 9.4, using principal axis estimation with maximum absolute correlations as initial communality estimates, and promax rotation to allow correlation among factors. Cumulative and incremental proportions of variance accounted for were examined, and scree plots were used to determine the optimal number of factors to be retained.

Results

Descriptive Statistics

Table 1 shows the descriptive statistics for the six executive function tests for younger and older adults. Younger adults out-performed both groups of older adults on all measures (all ps <.015). Young-older adults showed significantly less interference on the Stroop task, lower proportional number-letter shifting cost and greater accuracy on the updating tasks than old-older adults (ps < .038), but age differences on the Simon and global-local shifting tasks were not significant (ps > .125), although in the expected direction. Because of the difference in the proportions of men and women across groups, we also looked at sex differences. There were no significant differences as a function of sex for any of the executive function tasks in the young group (ps > .110). In the young-older group, men showed smaller inhibition costs than women on the Simon task [.04 difference, t(100) = 2.17, p = .033]. In the old-older group, men out-performed women on consonant updating [.09 difference, t(123) = 2.61, p = .010]. There were no age differences between men and women in any of the groups (ps > .635).

Table 1.

Descriptive statistics for the dependent measures

	N	Mean	SD	Range	Skewness	Kurtosis
Young adults
Inhibition
Stroop	124	−.31	.11	−.58, −.01	.21	−.13
Simon	124	−.09	.08	−.35, .06	−.58	.49
Updating
Keep track	124	.80	.10	.57, 1.0	−.17	−.48
Consonant updating	124	.69	.18	.25, 1.0	−.36	−.36
Shifting
Number-Letter (ms)	124	−353.78	196.00	−1091.16, −15.02	−1.25	2.36
Global-Local (ms)	124	−675.80	365.77	−3105.73, −175.25	−2.97	15.26
Proportional Number-Letter	124	−.47	.25	−1.48, −.03	−1.34	3.06
Proportional Global-Local	124	−1.29	.68	−5.44, −.34	−2.51	10.90
Young-older adults
Inhibition
Stroop	120	−.43	.09	−.68, −.19	−.10	−.22
Simon	102	−.15	.09	−.41, .02	−.43	.21
Updating
Keep track	120	.69	.11	.47, .90	−.06	−.80
Consonant updating	120	.57	.22	.00, .96	−.29	−.65
Shifting
Number-Letter (ms)	120	−562.04	251.51	−1627.15, −80.45	−1.09	2.56
Global-Local (ms)	120	−1383.78	679.40	−3751.00, −298.50	−1.41	2.59
Proportional Number-Letter	120	−.55	.23	−1.31, −.06	−.81	1.40
Proportional Global-Local	120	−1.87	.92	−5.16, −.21	−1.0	1.41
Old-older adults
Inhibition
Stroop	125	−.46	.11	−.79, −.05	.37	1.69
Simon	87	−.17	.10	−.36, .13	.02	−.16
Updating
Keep Track	125	.64	.12	.33, .90	−.46	.17
Consonant Updating	125	.50	.20	.02, 1.0	.09	−.25
Shifting
Number-Letter (ms)	125	−718.55	422.73	−2564.98, −132.39	−1.38	2.60
Global-Local (ms)	125	−1636.50	900.55	−5034.77, −321.31	−1.51	2.56
Proportional Number-Letter	125	−.62	.33	−1.81, −.14	−1.11	1.30
Proportional Global-Local	125	−2.07	1.12	−5.89, −.49	−1.21	1.49

Note. For all three groups, the proportional shift costs were logarithmically transformed to normalize the distributions for the confirmatory factor analysis.

Table 2 shows the zero-order correlations among the six measures and age for each of the three groups.¹ Note that overall the zero-order correlations across tasks are relatively low, which is typical for executive function tasks (Miyake et al., 2000, rs = −.05 to .34; see also Friedman & Miyake, 2017), but in none of the groups were the Stroop and Simon tasks correlated (rs = 0 to .09). For young adults, the two tasks associated with each of the updating and shifting functions respectively were significantly correlated with each other (r = .33 and .24, ps < .01) and were less or not at all correlated with any of the other tasks. Similarly, both of the older groups showed significant correlations between the two tasks associated with updating and shifting respectively (rs = .33 and .35 for young-older, and rs = .20 and .34 for old-older). However, the older adults also tended to show more correlations across executive function categories. For example, the Stroop task was correlated with one of the updating tasks in both older groups and also with one of the shifting tasks in the young-older group. In the young-older group, one of the shifting tasks was correlated with one of the updating tasks. Within all age groups, most tasks were not correlated with age. Because the Simon and Stroop tasks were not correlated with each other in any of the groups, we expected that they might not cohere well in a factor analysis, particularly in the older groups (rs = .04 and −.00).. This was confirmed in our initial CFA. The configural model had acceptable fit indices, and the three-factor model was identified in the young adults (although factors were not significantly correlated). In both of the older groups, however, correlations between the Inhibition factor and the other factors were greater than 1.0, indicating model misspecification. In addition neither the Simon or the Stroop tasksloaded significantly to the Inhibition factor in our older groups, and so a three-factor model could not be established. Because most studies have included the Stroop task as an indicator of Inhibition, and we lacked complete data for the Simon test in the two older adult groups, we decided to remove the Simon task from further consideration and retain the more commonly-used Stroop test as the only indicator of Inhibition, in order to make the systematic comparison across groups. We then re-estimated the three-factor configural model, with the five remaining tests.

Table 2.

Correlations Between Executive Function Tasks and Age in each group.

	1	2	3	4	5	6	7
Young adults (N = 124)
1. Stroop	—
2. Simon	.09	—
3. Keep Track	.00	.16	—
4. Consonant Updating	.08	.17	.33**	—
5. Proportional Number-Letter	.07	.18*	.14	.11	—
6. Proportional Global-Local	.19*	.05	−.06	−.07	.24**	—
7. Age	−.07	−.03	.19*	.08	.08	−.21*	—
	1	2	3	4	5	6	7
Young-older adults (N = 120)
1. Stroop	—
2. Simon (N = 102)	.04	—
3. Keep Track	.13	.01	—
4. Consonant Updating	.23*	.01	.33**	—
5. Proportional Number-Letter	.20*	.05	.08	.13	—
6. Proportional Global-Local	.16	.08	.30**	.06	.35**	—
7. Age	−.10	−.02	−.21*	−.15	−.04	−.13	—
	1	2	3	4	5	6	7
Old-older adults (N = 125)
1. Stroop	—
2. Simon (N = 87)	−.00	—
3. Keep Track	.13	.12	—
4. Consonant Updating	.20*	.22*	.20*	—
5. Proportional Number-Letter	.16	.23*	.12	.22*	—
6. Proportional Global-Local	.01	.14	.14	.08	.34**	—
7. Age	−.06	−.17	−.10	.05	−.15	−.05	—

^*p < .05;

^**p < .01.

Multiple-Group Confirmatory Factor Analyses (CFAs)

The configural model, which had no equality constraints, tested whether the three age groups shared the same general three-factor structure. As seen in Table 3, the configural model showed a significant χ², and the other fit indices were also weak, indicating that the three groups did not share the same general three-factor structure. We interpreted this to mean that the three-factor structure specified by Miyake et al. (2000) did not fit all three age groups. We therefore proceeded to model the latent structure separately for each of the age groups.

Table 3.

Multi-group CFA conducted based on Miyake et al.’s (2000) 3-factor model.

Model	df	χ2	p	AIC	SRMR	CFI	IFI	RMSEA
3-group CFA	15	26.641	.032*	86.641	.061	.867	.887	.080

^*p < .05.

We performed separate CFAs within each age group, testing and comparing the fit of the 6 different model specifications evaluated by Miyake et al. (2000). As shown in Table 4, both models 1 and 4 had acceptable fits in young adults. However, for model 4, one factor loading estimate was higher than 1.0 and there was a negative error estimate, indicating model misspecification. The full three-factor model (model 1) was therefore considered to be the best fitting model. Figure 1 shows this model and its estimated factor loadings. Here it can be noted that the Inhibition and Shifting factors were weakly correlated (r = .27), but unlike Miyake et al.’s findings, the other correlations between factors were very low and non-significant.

Table 4.

CFA based on Miyake et al.’s (2000) 3-factor model in young adults (N = 124).

Model	df	χ2	p	AIC	SRMR	CFI	IFI	RMSEA
1. Full three-factor	5	7.925	.160	27.925	.059	.906	.919	.069
2. One-factor	5	22.482	<.001**	42.482	.104	.439	.516	.169
Two-factor models
3. Shifting = Updating	5	22.482	<.001**	42.482	.104	.439	.516	.169
4. Shifting = Inhibition	5	7.205	.206	27.205	.064	.929	.939	.060
5. Updating = Inhibition	5	11.517	.042*	31.517	.082	.791	.820	.103
6. Independent three factors	8	12.763	.120	26.763	.083	.847	.856	.070

^*p < .05;

^**p < .01.

Figure 1.

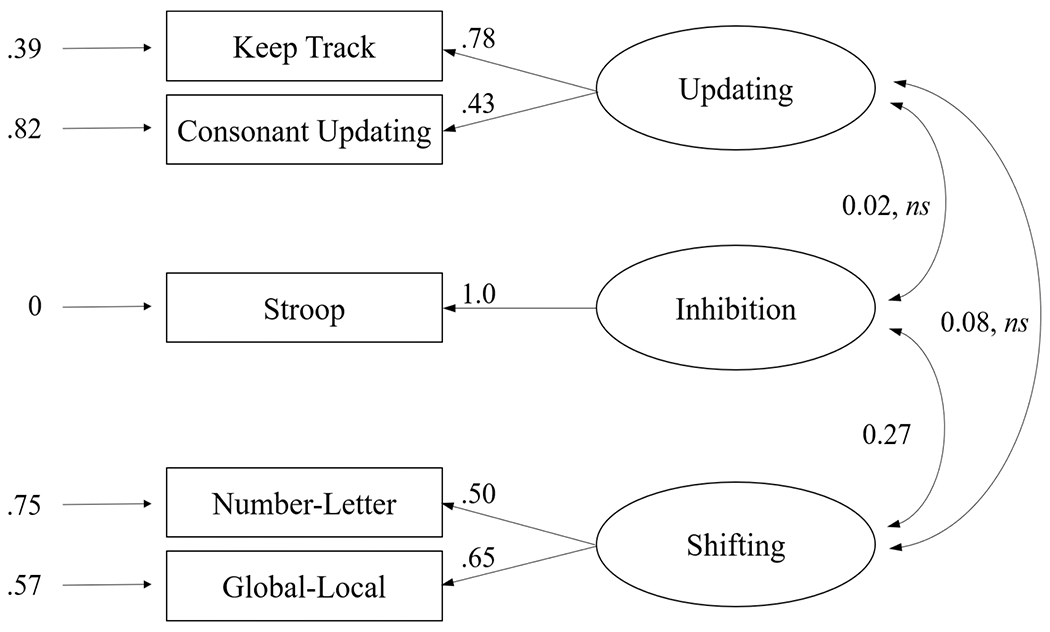
The estimated three-factor model for young adults (Model 1). Small single-headed arrows on the left indicate error variance, which was set to 0 for the Stroop task. Double-headed arrows represent correlations among the factors. ns = not significant.

In the young-older group, none of the models tested achieved an acceptable fit (see Table 5). To explore the factor structure of this group further, we conducted an exploratory factor analysis (EFA), using PROC FACTOR in SAS 9.4. The EFA revealed a two-factor solution (see Table 6), with one factor associated with the updating tasks and the Stroop test—labeled an Updating/Inhibition factor—and the other factor representing the shifting tasks. This model accounted for 96.6% of the variance and the two factors were moderately correlated (r = .30).

Table 5.

CFA based on Miyake et al.’s (2000) 3-factor model in young-older adults (N = 120)

Model	df	χ2	p	AIC	SRMR	CFI	IFI	RMSEA
1. Full three-factor	5	11.100	.049*	31.100	.063	.808	.834	.101
2. One-factor	5	14.309	.014*	34.309	.073	.707	.747	.125
Two-factor models
3. Shifting = Updating	5	14.309	.014*	34.309	.073	.707	.747	.125
4. Shifting = Inhibition	5	10.782	.056	30.782	.064	.818	.843	.099
5. Updating = Inhibition	5	12.039	.034*	32.039	.065	.778	.809	.109
6. Independent three factors	8	23.170	.003**	37.170	.118	.522	.551	.126

^*p < .05;

^**p < .01.

Table 6.

Factor loadings for 2-factor EFA in young-older adults (N = 120).

	Updating/Inhibition (Factor 1)	Shifting (Factor 2)
Stroop	.36	.12
Consonant Updating	.64	−.12
Keep Track	.42	.27
Proportional Global-Local	−.05	.57
Proportional Number-Letter	.10	.35

For the old-older adults, the only acceptable model from the CFA was Model 5 (see Table 7), which had the lowest AIC value and a CFI score above .95 indicating a close fit. This model was a two-factor solution with updating and inhibition tasks accounting for one factor, and shifting tasks supported by the other factor. The estimated factor loadings are illustrated in Figure 2, which also shows that the two factors for this group were strongly correlated (r = .53). Comparison of the correlational coefficients for the two older groups, after Fisher r-to-z transformation, indicated that the correlation between the two factors was significantly greater in the old-older group than the young-older group (Z = 2.17, p = .030).²

Table 7.

CFA based on Miyake et al.’s (2000) 3-factor model in old-older adults (N = 125).

Model	df	χ2	p	AIC	SRMR	CFI	IFI	RMSEA
1. Full three-factor	5	7.616	.179	27.616	.061	.895	.912	.065
2. One-factor	5	7.533	.184	27.533	.054	.898	.915	.064
Two-factor models
3. Shifting = Updating	5	7.533	.184	27.533	.054	.898	.915	.064
4. Shifting = Inhibition	5	7.729	.172	27.729	.061	.890	.909	.066
5. Updating = Inhibition	5	5.606	.347	25.606	.052	.976	.980	.031
6. Independent three factors	8	18.468	.018*	32.468	.111	.579	.610	.103

^*p < .05.

Figure 2.

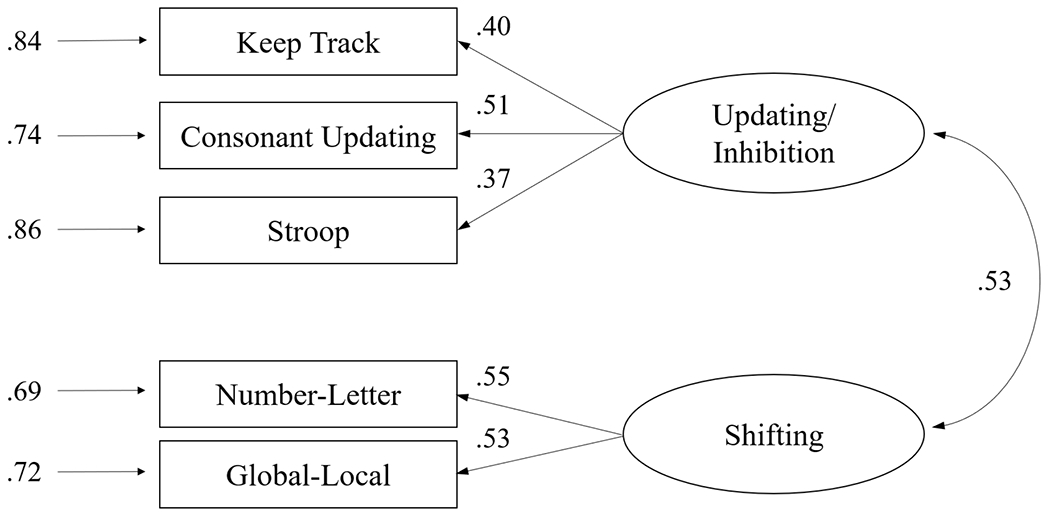
The estimated two-factor model for old-older adults (Model 5). Small single-headed arrows on the left indicate error variance. Double-headed arrows represent correlations among the factors.

To explore further the shared variance between the two factors in our old-older group, we tested two nested factors models similar to those tested by Friedman et al. (2008, 2011). The first model, which included a Common EF factor, an Updating/Inhibition factor, and a Shifting factor produced a negative error estimate and therefore could not be specified. In the second model, updating tests and the Stroop task were specified to load directly to the Common EF factor, along with a separate, Shifting-specific factor. This model had excellent fit indices, χ² (4) = 1.823, p = .768, CFI = 1.000, RMSEA = .000. As can be seen in Figure 3, four of the five tasks loaded significantly to the Common EF factor, and both of the shifting tasks loaded significantly to the Shifting-specific factor. The number-letter shifting task also shared a significant amount of its variance with the Common EF factor, but the loading of the global-local task to the Common EF factor was not significant.³

Figure 3.

The estimated nested factor model for old-older adults. Small single-headed arrows on the left indicate error variance. ns = not significant.

Discussion

The results of the present study were both consistent and inconsistent with previous findings. Consistent with several studies, a three-factor structure of executive function was found in young adults, suggesting that shifting, updating, and inhibition (particularly Stroop-related inhibition) represent independent components of executive function. However, unlike the Miyake et al. (2000) study, which found those three factors to be moderately correlated in young people (.42 - .63), the factors were either uncorrelated or weakly correlated in our young group (.02 - .27). In addition, in the present study, using identical tests for the young and older adults, we demonstrated a pattern of increasing correlations among the executive function components with increasing age and a greater reliance on general control processes.

The Three-Factor Model in Young Adults

Although we were able to identify three independent factors of shifting, updating and inhibition in young adults, the factors in our study were largely uncorrelated. The difference between our study and those of Miyake, Friedman and colleagues may be at least partly attributable to differences in the specific measures submitted for analysis. We used a measure of global shift costs for both of our shifting tasks. In Miyake et al.’s (2000) study, three shifting tasks each used a different measure, mixing global and local shift costs, and in several later studies, only local shift costs were measured. As noted previously, compared to young adults, older adults show deficits in global shift costs but not in local shift costs (e.g., Gamboz et al., 2009; Verhaeghen & Cerella, 2008), suggesting that the two types of shifting access different cognitive processes that are differentially affected by aging. They also rely on different brain regions (e.g., Braver et al., 2003). Thus the shared variance in the shift costs reported by Miyake et al. (2000; Friedman et al., 2008) may represent something other than the global shift costs measured in our study, and may have contributed to correlations between the Shifting and Updating factors in those earlier studies. We should also note that in a recent paper with young adults, Smith, Banich, & Friedman (2019) looked at mixing costs, comparing repeat trials in shift and no-shift blocks, and reported that a mixing cost factor did not correlate with their shifting-specific factor, which was based on local shift costs. Finally, Gamboz et al. (2009) compared the three kinds of costs in the number-letter task in both young and older adults, and found that global and mixing costs showed age-related deficits, but local shift costs did not. They concluded that global and mixing costs may be attributable to a failure to control interference between two goals being held continuously in mind over time. This is required in mixed blocks but not in single blocks. Local shift costs, which are measured between trials within a mixed block, may depend more on the ability to switch rapidly between two task sets or goals in response to a cue. Similarly, Braver et al. (2003; Braver 2012) have suggested that global shift costs reflect the sustained or active maintenance of goals over a block of trials, whereas local shifts depend on transient trial-to-trial reactivations of the appropriate goal for a specific trial (see also Dörrenbächer, Wu, Zimmer, & Kray, 2020).

These differences between the two kinds of shifting costs may account for the different outcomes across studies, and suggest that if we had looked at local shift costs in our models, we might have found correlated factors in young adults as in previous studies. However, when we substituted local shift costs for global shift costs in our CFAs, the Shifting factor could not be identified in either the young or the old-older group and the two local shift cost measures did not load significantly to Shifting. This may have occurred because we had only two indicators of the Shifting factor. Interestingly, a follow-up EFA in the young adults produced a weakly-correlated (r = .23) two-factor solution with the two shifting tasks loading to different factors: Number-letter loaded with the updating tasks and global local loaded with Stroop. These findings indicate that the local shift costs from our two tasks do not reflect the same underlying processes, and that our two shifting tasks differ from each other. We will return to this issue later in the discussion of the nested factor model in our old-older group. Overall, these findings highlight the complexity of executive control functions involved in any single task and the importance of considering more closely the specific processes supporting the tasks, not just the tasks themselves (see also Miyake & Friedman, 2012; Stuss & Craik, 2020).

For the Updating factor, the two measures that we analyzed were almost identical to those used by Miyake et al. (2000). Our keep track task, however, was somewhat easier than Miyake et al.’s, requiring that people keep track of 1-4 categories at a time rather than 4 and 5 categories. The task for our young adults may therefore have been less challenging than it was for the young people in the Miyake et al. study, although performance was not at the ceiling. Young adults in the present study recalled 80% of the items, whereas in Miyake et al. they recalled just 58%. Miyake et al. also had a third task in the Updating factor, tone-monitoring, which they found actually loaded on their Inhibition component in an exploratory factor analysis, perhaps accounting for the Updating-Inhibition correlation in their study.

Our two inhibition tasks were completely uncorrelated in both young and older adults and did not cohere in either of the older groups in the preliminary CFA. As noted in the Introduction, other investigators have also had problems identifying inhibition tasks that would load together from a single latent variable. Rather than drop the Inhibition factor from our model, however, we decided to retain it even though it had only one indicator, the Stroop test. For the young adults in our study, the Stroop test clearly captured processes that were independent of those involved in shifting and updating, and so it seemed important to include it as representing a different component of executive function in this group. Inhibition has also been an important construct in the neuropsychological literature, not only in theories of executive function and dysfunction, but also in theories of aging (e.g., Hasher, Lustig, & Zacks, 2007). Neuroimaging studies (e.g., Aron, Robbins, & Poldrack, 2014; Collette et al., 2005) have indicated that inhibition involves a variety of areas of prefrontal cortex depending on the task, consistent both with its characterization as a component of executive control and with its multifaceted nature. Although it has been difficult to measure or to identify the specific processes involved in its expression, inhibition nevertheless appears to be an important component of executive control that should be considered (see also Friedman et al., 2008).

Finally, in our young adult group we observed only one weak correlation among the factors—between Inhibition and Shifting—but no correlations between the other factors. One possible reason for the lack of correlation between Shifting and Updating might be the use of global shift costs rather than local shift costs. As outlined earlier, these two types of shift costs clearly reflect different processes. Perhaps local shifts require processes that overlap with those engaged by updating (and inhibition) to a greater degree than global shifts. A possible candidate might be overall speed of information processing, which might be common to several tasks (see Hedden & Yoon, 2006; Smith et al., 2019). In our study, we controlled for individual differences in baseline response speed by using proportional differences in RTs rather than absolute differences or raw RTs, which many studies have used. The small correlation between Shifting and Inhibition in our young people, however, may reflect a speed component specific to the selection of one of two possible responses. Alternatively, differences between our two shifting tasks may have affected the correlations between the Shifting factor and the other latent factors.

Models of Executive Function in Older Adults

In the present study, we were able to administer the identical tests to our older and young adults, with approximately the same numbers of participants in each group (Ns = 120-125), spanning the same number of years (approximately 14 years represented in each group; ages 18-32 in young, 60-73 in young-older, and 74-87 in the old-older group except for 5 people over 90). This allowed us to make comparisons across age groups that were more direct than those made previously and could not be interpreted in terms of different tests, measures or conditions across groups.

The pattern that emerged with age showed a reduction from three executive function factors to two in the older groups, and increased correlations among the two factors with increasing age. In the young-older group, although none of the CFA models had acceptable fit indices, the EFA yielded two modestly correlated factors (r = .30) for Shifting and Updating with the Stroop test loading with updating tasks. Similarly, the best-fitting CFA model for the old-older group indicated two factors of Updating/Inhibition (i.e., Stroop) and Shifting, which were even more strongly correlated (r = .53). Thus, although in young adults the Stroop test appeared to rely on processes that were completely independent of those involved in updating tasks, in older adults the updating and Stroop tasks appeared to depend at least partly on common processes. Furthermore, at the oldest ages, there was even greater overlap in the processes supporting the different executive function tasks, indicated by the increasingly stronger correlations between the two factors.

To gain further understanding of the processes underlying the increasing shared variance with age, we tested a nested factors model in our oldest group, similar to one that Friedman et al. (2008) had demonstrated in young adults. Here we found that a single EF factor accounted for a significant amount of variance in all of the individual tasks except the global-local shifting task, and captured all of the variance in the Updating/Inhibition factor. There was also a shifting-specific factor, which accounted for additional variance shared by the two shifting tasks. These results suggested that a common factor supported performance on the updating, Stroop, and number-letter tasks, but not on the global-local task. This finding invited two questions: What processes does this common factor represent, and why, as people get older, do they rely increasingly on those processes? Because we do not know what the common factor represents, and although it does not include all of the tasks in this study, we will continue to refer to it as a common factor, as we explore what processes might be involved.

The Common Factor and Aging

In Friedman et al.’s (2008) study in young people, all of the individual tasks loaded to the Common factor; shifting and updating measures retained factor-specific variance, but inhibition was captured entirely by the Common factor. They proposed that the Common EF factor represented the maintenance of task goals in the face of interference, and the implementation of those goals to affect or bias performance (see also, Friedman & Miyake, 2017; Miyake & Freedman, 2012). We considered whether this characterization could account for the common factor in our model. In our study, the global-local shifting test was not represented in the common factor although number-letter shifting was. We decided therefore to look at differences between these two tasks to help us get a clearer picture of what processes might be captured by our common factor.

The two shifting tasks in our study differed with respect to the predictability of the behavioral response. In the number-letter task, the pattern of responses was predictable (repeat-switch-repeat-switch, i.e., letter-letter-number-number-letter-letter…) throughout the mixed block. This allowed people to prepare for an upcoming response before the actual appearance of the stimulus. In our global-local task, the pattern was random. So the category of response could not be determined until the stimulus itself was presented. In this task, although the goals or rules had to be maintained, they could not effectively bias the upcoming response. The color of the stimulus itself indicated which feature of the stimulus should be identified—global or local. Similarly, for all of the other tasks that loaded to our common factor, the category of the response or the rule was available prior to the presentation of the stimulus, enabling one to prepare for and optimize the upcoming response. The common factor appeared to come into play when an informative cue preceded the stimulus, and a preparatory response could be made. We therefore suggest an addition to the Friedman et al. (2008) interpretation: that the common factor involves the planning or preparation of a response, based on task goals that are held continuously in mind along with other predictive information or cues that might facilitate performance.

This view is similar to one proposed by Braver (2012; see also Friedman & Miyake, 2017). Braver distinguished between proactive control, which involves “sustained and anticipatory maintenance of goal-relevant information…to enable optimal cognitive performance,” and reactive control, which is “stimulus-driven” and “transient” (pp. 106). This distinction also maps onto the distinction between global and local shifting costs discussed earlier, but can be applied more broadly across executive function tasks in general. Braver (2012) also noted that proactive control is resource-demanding, particularly when two goals have to be maintained over time, and is therefore likely to be implemented only when strong and reliable cues are available. In the present study, there were no pre-cues available in the global-local task, and thus no reason for older adults, who may have reduced attentional resources, to continuously maintain the two goals required by the task. Instead, in the interest of conserving resources, they may have opted to wait for the stimulus and then activate the indicated goal and make the response. Activation and re-setting of the appropriate goal and response during each trial might be the role of the shifting-specific executive component. For the number-letter task, the switch-repeat pattern of the stimulus presentations provided reliable knowledge of the relevant upcoming task, thus favoring a preparatory response to optimize the subsequent behavioral response.

In our oldest group, the variance shared by updating and inhibition was accounted for entirely by the common factor. The reduction from three to two separate factors in older adults therefore may be driven by an increased reliance on proactive control, by taking advantage of predictive cues or other information that can enhance performance. Global shifting tasks, however, may still rely on domain-specific shifting processes, namely reactivation of goals when the stimulus is presented, although there may be differences across tasks that determine the extent to which the common factor may be engaged as well. In some cases both kinds of control might be involved to varying degrees.

Why then might older adults rely more on the common factor for many tasks? One possibility is that their behavior reflects reduced cognitive resources (Craik & Byrd, 1982). In order to perform these and many other executive function tasks, goals must be kept in mind and sustained over time. To the extent that long-term goal maintenance is resource-demanding, few resources may be available to perform other demanding tasks such as updating. If the task rule is simple and clearly informative (e.g., name the color; recall the last four letters), tasks may be accomplished quickly and accurately by way of a preparatory response, with no need to engage additional domain-specific processes. If, however, the rule is complex and does not permit a preparatory response as in the global-local task (i.e., if the figure is blue identify the global shape, and if the figure is black identify the local shapes), it may be more efficient to focus on trial-to-trial demands of the task than to expend resources on the continuous maintenance of a complex rule. This could account for the finding in the old-older adults that the global-local task did not engage the common factor.

We suggest further that the reduction in domain-specific factors with increasing age may reflect a strategy by older people to allocate their limited resources in a way that optimizes the likelihood of an accurate response. In the case of pre-cued tasks or those with a simple or continuously visible rule that applies across a block of trials, the optimal strategy may be to focus on the cue or rule and form a preparatory response. In the case of uncued tasks, the most efficient strategy may be to focus on bottom-up, stimulus-driven characteristics to determine and activate the appropriate response on each individual trial. For young people, resource demands may not be an issue. So, in updating tasks for example, they may be able to easily hold the overall goal in mind while at the same time focus resources on updating-specific processes (e.g., adding and deleting items from working memory). They therefore may draw on both the common factor and updating-specific processes, as found in Friedman et al (2008). On the other hand, the Stroop test may best be accomplished by simply focusing on the simple rule (i.e., name the color) and prepare to respond, and so the common factor is accessed, as is the case for the updating tasks. It should be noted, however, that if the rule changed randomly across trials, older adults might not keep the rule in mind, and the Stroop task might load with the shifting tasks. This again speaks to the importance of identifying processes, not just tasks.

This explanation of age-related differences seems to fit our data well. It is also compatible with a compensation model of cognitive aging (Buckner, 2004; Reuter-Lorenz & Cappell, 2008), which states that as tasks become more difficult with age and neural function becomes less efficient, older adults may recruit additional relevant processes or resources to get the job done. We suggest that some older adults might also, under some conditions, reallocate their limited resources strategically to optimize performance, or (in Braver’s terms), switch from a proactive to a reactive strategy. Whether this is a strategy engaged purposefully by older people or is an inevitable consequence of aging cannot be determined by the present study, but could be tested in future studies by manipulating the predictability and difficulty of executive function tasks. We should note also that there are substantial individual differences. Some older adults might compensate or allocate more effectively than others and reach performance levels close to those of younger adults (cf., Cabela, Anderson, Locantore, & McIntosh, 2002; Angel et al, 2016). Although the older adults in our study performed more poorly on average than younger adults, one can see (Table 1) that the distributions are overlapping, so that some older adults were performing at the level of young adults. At the same time, there may be biological and pathological changes that occur with age which, although undetected by our screening procedures, may contribute to the cognitive heterogeneity that we see even in apparently healthy community-dwelling adults. Further studies might explore the extent to which patterns of correlation differ across different groups of older adults (e.g., higher vs lower function; see deFrias, Dixon, & Strauss, 2009) and the possible reasons for these individual differences.

The present findings, with respect to age-related changes, might also be interpreted in terms of dedifferentiation, a theory of aging that predicts larger correlations and fewer distinct factors in older adults as neural integrity declines and executive functions deteriorate (for discussion, see Adrover-Roig et al., 2012; Anstey, Hofer, & Luszcz, 2003; Hull et al., 2008). This theory places greater emphasis on the decreasing availability of specific processes rather than on resources per se, and suggests a kind of inevitability in aging that would eventually result in a single, common factor. In our data, however, even in the oldest group, two factors persisted; the correlation between them did not approach 1.0, and shifting continued to account for independent variance. As noted above, however, there are individual differences. Our older people were quite well-educated. It is possible that people who are lower functioning may show complete dedifferentiation (see deFrias et al., 2009). Others have suggested that a common factor may be working memory (cf., Kimberg & Farah, 1993), executive attention (Kane, Conway, Hambrick & Engle, 2007) or attentional resources (e.g., Reuter-Lorenz & Jonides, 2007). A recent study (Zuber, Ihle, Loaiza, Schnitzspahn…Kliegel, 2019) looking at the contribution of the three executive function components to working memory in young and older adults, reported that updating and inhibition, but not shifting (as measured by global shift costs), accounted for age-related variance in working memory, consistent with the idea that working memory might be a factor common to many tasks, although not the only factor.

In the present study, we did not detect a factor in our older adults that was common to all of our executive function tasks. Instead, a two-factor model with increasing correlations with age, most accurately accounts for our data. Our findings also suggest that older adults perform executive function tasks differently than young adults. In our oldest adult group, the two factors might be Planning (or some combination of goal maintenance and response preparation) and Switching, which map onto Braver’s (2012) Proactive vs Reactive Control functions. These labels might also be applicable to younger people, although contributing tasks might be different. Characterization in terms of processes rather than tasks might also suggest a different selection of executive function tests in future studies that could continue to add to our understanding of how executive functions change with age.

In summary, the results suggest that there are age-related differences in the deployment of executive functions, which may involve the recruitment of fewer domain-specific processes and a greater reliance on general executive control mechanisms as people age. However, this does not seem to reflect dedifferentiation, but rather suggests that older adults perform these tasks differently than young adults (see also Gajewski, Hanisch, Falkenstein, Thönes & Wascher, 2018; Hull et al., 2008), perhaps reflecting a reduction and strategic reallocation of cognitive resources, which may differ across tasks and individuals.

Limitations and Conclusions

There were, of course, some limitations to the present study, most importantly the small number of indicators for each latent variable, particularly Inhibition. Most of the tasks that we used, however, with the exception of the Simon task, had previously been identified in several studies as contributors to the three latent variables that were proposed, and some studies had identified the 3-factor structure with only two indicators for some factors (e.g., Gustavson et al., 2018; Smolker et al., 2018). However, having only two indicators for each latent variable is not optimal; it may in some cases make the identification of shared processes less certain and may have affected the strength of the correlations between factors in our young group. Also the fact that our two shifting tasks, although clearly loading together to the Shifting factor, differed with respect to another important process, may have influenced the correlations with the other factors. However, at the same time, this result provided valuable new information about the Common EF factor in the oldest adults, and highlighted the importance of paying attention not just to the specific tasks or measures contributing to the latent variables, but also to the specific processes involved.

Inhibition, in general, has been a difficult construct to identify at the latent variable level as was the case in the present study, and may itself be decomposed into different sub-processes (Friedman & Miyake, 2004; Hedden & Yoon, 2006). Having only the Stroop test as a single indicator, along with its lack of correlation with the Simon task, made it difficult to determine with any confidence what specific process might be engaged by this task, particularly in the young group. In the older groups, however, the Stroop test loaded clearly with the updating tasks, and ultimately contributed to our understanding of the common factor in terms of response preparation or planning. It is possible, however, that if there were other additional indicators of Inhibition, a separate Inhibition factor might have been retained in the older adult groups, capturing a different facet of this multi-dimensional construct.

The young-older group was difficult to characterize initially. None of the models that we tested in the CFA were acceptable. However, when viewed in the context of the overall findings, it seems clear that this group fell intermediate between the young and the old-older group: executive functions were reduced from three factors in young adults to two in this group, and correlations between the factors were much stronger in the old-older group than in the young-older group. The young-older adults (aged 60-73) may have been in a kind of transition phase with some performing more like the young and others more like those in oldest group. We can see, however, that even in the oldest group, people still appear to access some of the same specific executive processes as young people. It may be that, as they get older, people try to allocate their resources more strategically, sometimes calling on broadly applicable control processes and other times focusing on more-specific processes. Further research might explore the extent to which such strategies might be modified with training (see Dörrenbächer et al., 2020), enabling older people to select the optimal strategy depending on tasks demands.

The findings of this study and those of other studies using a CFA or latent variable approach also highlight the benefits of using a set of executive function tests that may tap into different executive processes, while at the same time allowing one to identify common processes. From a clinical or rehabilitation perspective, it seems important to be able to assess the specificity of an executive function deficit so that interventions can be focused on the particular processes involved. From an empirical and theoretical perspective, these findings provide additional information about what, how and why executive functions may change with age, and raise the possibility that all executive functions may not decline or decline at the same rate. There is clearly much more to be learned. How and why are some older adults able to compensate or allocate resources more effectively than others? Can we devise strategies that will allow people to use preserved or less demanding executive functions to compensate for other functions that may be compromised or overly taxing? Can we identify more precisely what brain regions are associated with each of these functions, how they change with age, and how they interact to produce more complex executive behaviors? In order to answer these questions we need to be able to characterize executive functions more precisely and continue to devise and evaluate new test instruments to improve our diagnostic capabilities and treatments. The use of composite measures of each function, as opposed to a single test, also increases our ability to identify the specific component processes, and gives us greater power to predict and understand other cognitive processes and behaviors that might depend on them. Neuroimaging studies (e.g., Smolker et al., 2018) have begun to relate different executive processes to differences in brain structure and activity, and these kinds of studies will also contribute significantly to our further understanding of executive functions and the mechanisms underlying differences among cognitively healthy older adults.