Fig. 4. Thresholds for the XZZX code using a matching decoder.
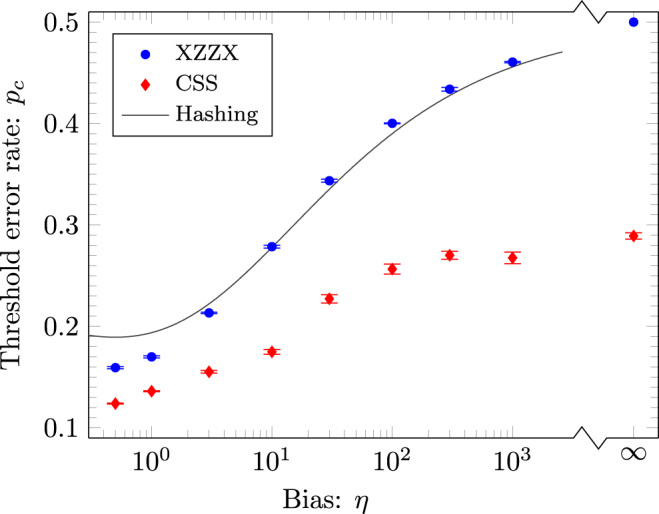
Code-capacity thresholds pc for the XZZX code with rectangular boundary conditions (as in Fig. 1h) shown as a function of noise bias η using a matching decoder. The threshold error rates for the XZZX code experiencing Pauli-Z-biased noise (blue) significantly outperform those found using the matching decoder presented in ref. 10 experiencing Pauli-Y-biased noise for the CSS surface code (red). For the XZZX code, we evaluated separate thresholds for logical Pauli-X and Pauli-Z errors, with the lowest of the two shown here (although the discrepancy between the two different thresholds is negligible). Data points are found with ~105 Monte-Carlo samples for each physical error rate sampled and each lattice size used. We study the XZZX code for large lattices with dZ = AηdX where aspect ratios take values 1 ≤ Aη ≤ 157 such that A1/2 = 1 and A1000 = 157. We find the XZZX code matches the zero-rate hashing bound at η ~10 (solid line). For larger biases the data appear to exceed the hashing bound. For instance, at η = 100 we found pc − ph.b. ~ 1%. We obtained this threshold using code sizes dX = 7, 11, 15 and A100 = 23. Error bars indicate one standard deviation obtained by jackknife resampling over code distance.
