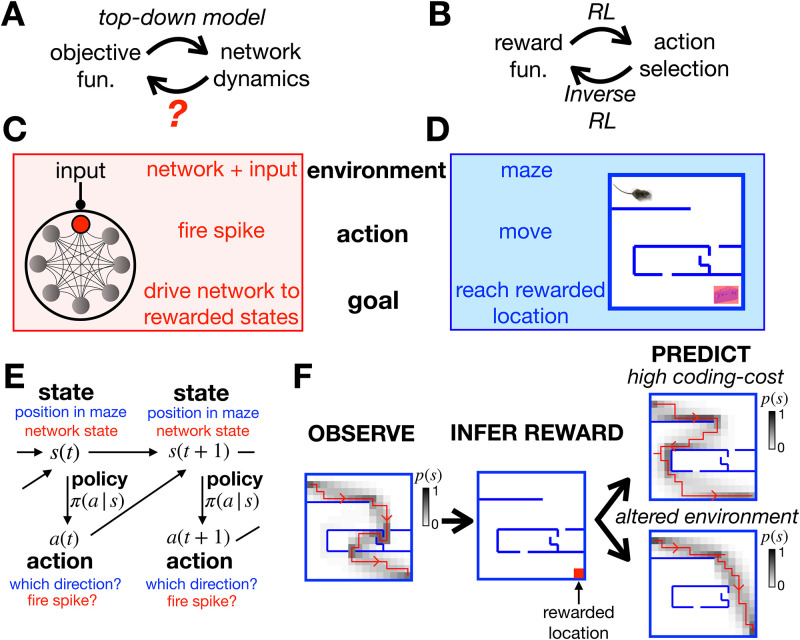
Fig 1. General approach.

(A) Top-down models use an assumed objective function to derive the optimal neural dynamics. The inverse problem is to infer the objective function from observed neural responses. (B) RL uses an assumed reward function to derive an optimal set of actions that an agent should perform in a given environment. Inverse RL infers the reward function from the agent’s actions. (C-D) A mapping between the neural network and textbook RL setup. (E) Both problems can be formulated as MDPs, where an agent (or neuron) can choose which actions, a, to perform to alter their state, s, and increase their reward. (F) Given a reward function and coding cost (which penalises complex policies), we can use entropy-regularised RL to derive the optimal policy (left). Here we plot a single trajectory sampled from the optimal policy (red), as well as how often the agent visits each location (shaded). Conversely, we can use inverse RL to infer the reward function from the agent’s policy (centre). We can then use the inferred reward to predict how the agent’s policy will change when we increase the coding cost to favour simpler (but less rewarded) trajectories (top right), or move the walls of the maze (bottom right).