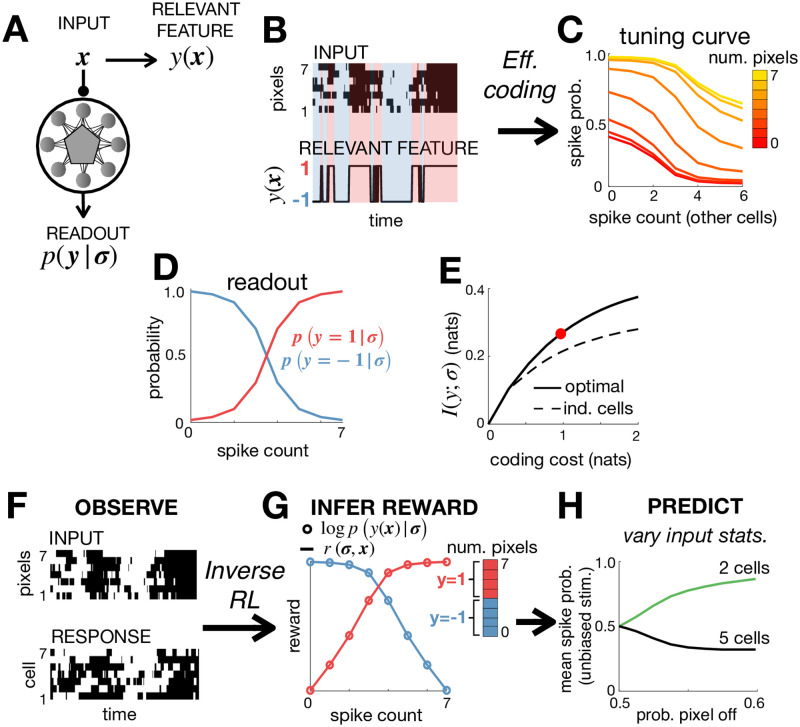
Fig 4. Efficient coding and inverse RL.

(A) The neural code was optimised to efficiently encode an external input, x, so as to maximise information about a relevant stimulus feature y(x). (B) The input, x consisted of 7 binary pixels. The relevant feature, y(x), was equal to 1 if >3 pixels were active, and -1 otherwise. (C) Optimising a network of 7 neurons to efficiently encode y(x) resulted in all neurons having identical tuning curves, which depended on the number of active pixels and total spike count. (D) The posterior probability that y = 1 varied monotonically with the spike count. (E) The optimised network encoded significantly more information about y(x) than a network of independent neurons with matching stimulus-dependent spiking probabilities, p(σ_i = 1|x). The coding cost used for the simulations in the other panels is indicated by a red circle. (F-G) We use the observed responses of the network (F) to infer the reward function optimised by the network, r(σ, x) (G). If the network efficiently encodes a relevant feature, y(x), then the inferred reward (solid lines) should be proportional to the log-posterior, logp(y(x)|σ) (empty circles). This allows us to (i) recover y(x) from observed neural responses, (ii) test whether this feature is encoded efficiently by the network. (H) We can use the inferred objective to predict how varying the input statistics, by reducing the probability that pixels are active, causes the population to split into two cell types, with different tuning curves and mean firing rates (right).