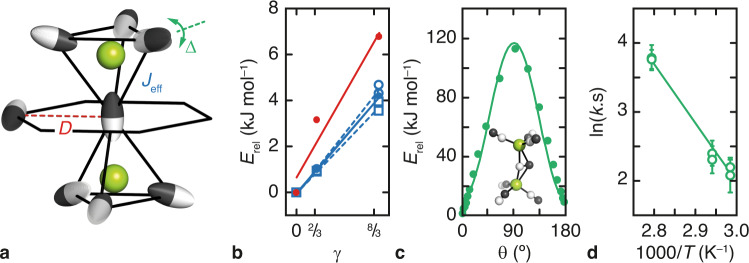
Fig. 3. Microscopic single-ion and pairwise interaction parameters in Cd(CN)₂.

a The effective exchange interaction (strength $J_{\mathrm{eff}}$) operates between nearest neighbours within the same pyrochlore sublattice. Dipolar interactions (strength $D$) give rise to an effective exchange interaction between nearest neighbours on alternate sublattices. The single-ion anisotropy term $△$ reflects the enthalpy barrier to CN^– reorientations. b Relative DFT energies $E_{\mathrm{rel}}$ for a series of single network (filled blue symbols) and interpenetrated (filled red symbols) Cd(CN)₂ configurations with different CdC_nN_4–n coordination environments: CdC₂N₂ (geometric parameter $\gamma =\frac{2}{3}{\left(n-2\right)}^2=0$), CdC₃N/CdCN₃ ($\gamma =\frac{2}{3}$) and CdC₄/CdN₄ ($\gamma =\frac{8}{3}$). Simple geometric arguments give $E_{\mathrm{rel}}=\gamma J_{\mathrm{eff}}$ and $\gamma \left(J_{\mathrm{eff}}+D\right)$ for single-network and interpenetrated Cd(CN)₂, respectively. The corresponding NMR-derived values are shown with open blue symbols (squares = ref. ³⁴ circles = this study). c Nudged elastic band calculation energies for a 180° CN^– orientation flip (filled green symbols) and corresponding fit $E_{\mathrm{rel}}\left(\theta \right)=△{\cos }^2\theta =△S_{\parallel }^2$ (solid green line), from which the value of $△$ was obtained. The $△\simeq$ 90° transition state involves a C-bridged Cd–(CN)–Cd linkage (inset) and a reduced Cd…Cd separation. d Arrhenius plot reflecting the temperature dependence of CN^– flipping rates as determined using ¹¹³Cd EXSY spectroscopy. Error bars denote the standard error in rate constants determined extracted during fitting (see Supplementary Figure 6 and Supplementary Table 7). The experimental value of $△$ is given by the gradient of the linear fit (solid line).