Abstract
We add a simple dynamic process for adaptive “social distancing” measures to a standard SIR model of the COVID pandemic. With a limited attention span and in the absence of a consistent long-term strategy against the pandemic, this process leads to a sweeping of an instability, i.e. fluctuations in the effective reproduction number around its bifurcation value of . While mitigating the pandemic in the short-run, this process remains intrinsically fragile and does not constitute a sustainable strategy that societies could follow for an extended period of time.
Keywords: COVID pandemic, SIR model, Social interaction
1. Introduction: Memoirs and dedication
Evolution, Money, War and Computers: Non-Traditional Applications of Computational Statistical Physics: The title of Dietrich Stauffer’s 1999 monograph with co-workers S. Moss de Oliveira and P.M.C. de Oliveira [1] only covers a few of the many research areas that Dietrich had pursued in his insatiable curiosity, thirst for knowledge and for helping to shed a scientific light on complex phenomena in nature and (more and more shifting his focus in his later years) in society. I have met Dietrich Stauffer first around 1998 probably in one of the then mushrooming workshops of the emerging ecophysics community. While I had been working on using statistical physics methodology for the analysis of models with interacting agents in economics since the early 1990s, as an economist I came to this circle as an outsider. I had become aware of some of the publications on scaling laws in economics by Gene Stanley, Rosario Mantegna, Sorin Solomon and others, and so made an attempt to connect with this new tribe. Not an insider to the physics community, my knowledge of their customs and conventions was very limited and this lack of familiarity has caused interesting and often quite controversial discussions with my new comrades, some of whom (like Dietrich) became close collaborators and co-authors.
I do not recall exactly at which occasion I first made the acquaintance with Dietrich, but because of the lucky coincidence of my move to Bonn University (10 km from Cologne) in 1998, we had many personal meetings between 1998 and 2000 in which we embarked on a joint research project and discussed about the different methodologies and scientific standards of our fields. For a few years, Dietrich also became an active member of the interdisciplinary crowd that attended the annual Workshops on Economics with Heterogeneous Interacting Agents (WEHIA). I vividly remember traveling to the 1999 workshop in Genoa and back in night trains together with Dietrich (wondering that he apparently had no luggage with him).
The interaction with the econphysicists brought me into contact with some strong personalities: I remember that when in a paper with one of my Ph.D. students we showed that a then prominent physics-inspired model of the stock market practically functioned like a random-number generator, the prominent author of this model used so strong language that my student felt intimidated for quite a while. Another time, when as a reviewer for a physics journal I pointed out a mathematical inconsistency in a submission by another well-cited physicist, this colleague revealed that he had known it before but claimed that the error could be resolved by metaphysical arguments (no references here as I do not want to compromise anybody).
Dietrich was definitely more easy going: A few years after the publication of our joint paper with massive simulations of two stock market models [2]. Dietrich informed me that some perplexingly regular oscillations reported in this paper were simply due to his use of prefabricated random numbers. In the old days, when memory space and computing time were sparse resources, he had generated a set of random numbers that he then had been using in many of his computational papers through the decades. Apparently, in 1999, simulating more than agents in the Kim-Markowitz model, the same limited set of random numbers had been fed into our simulations at the super computer at the German nuclear research center in Jülich again and again causing artificial oscillations in the output (apparently we did not make real good use of the super computer).
Dietrich’s curiosity would certainly have been instigated by the current pandemic, and if he were still among us, he by now would have published a few dozen papers on this phenomenon. He would probably have been intrigued by the unfolding dynamics and the different outcomes that different societies have so far reached in reaction to exactly the same challenge. In the following I will make a very preliminary attempt at modeling the social dynamics in the perception of and the reactions to the COVID pandemic using concepts from percolation theory to formalize adaptive human behavior in response to the unfolding crisis, in the spirit of Dietrich Stauffer’s contributions to socio-economic modeling.
2. The baseline approach to contagion: The SIR model
The biological processes at work in an epidemic are well understood. The seminal aggregate modeling framework in epidemiology is known as the SIR model with this acronym standing for susceptible (S), infected (I) and recovered (R) members of a population, cf. Anderson and May [3]. The SIR model can either be formulated as an agent-based model with stochastic transitions of agents between different states, or as a system of differential equations. Performing a mean-field approximation based on a Master equation and Fokker–Planck formalism, both approaches can easily be shown to be congruent. Here we adopt an agent-based approach.
Since COVID is a potentially fatal disease we will add the group of deceased persons (D) to the susceptible (S), infected (I) and recovered (R). From an overall population of N agents, each one at any time t will be in one of the four categories, so that
| (1) |
holds. In the spirit of computational models in statistical physics, the dynamics of the contagion process can be modeled with transition rates:
| (2) |
| (3) |
| (4) |
Eq. (2) defines the rate of infections which for diseases transmitted via human interaction is an increasing function of the number of currently infected and infectious agents, (we do not distinguish between infected and infectious although for a detailed mapping of the empirical process this might be required). Eqs. (3), (4) define the recovery rate, , and the death rate, , respectively that are both assumed to be constant. All these rates are understood as Poisson transition rates in a continuous-time setting (i.e., what is also called a jump Markov process).
Applied empirical modeling would add further refinements like an age structure of the population, regional disaggregation with possible networks of communication through which the spread of the virus could proceed, and other factors, but would still preserve the basic features of the model, cf. Tolić et al. [4].
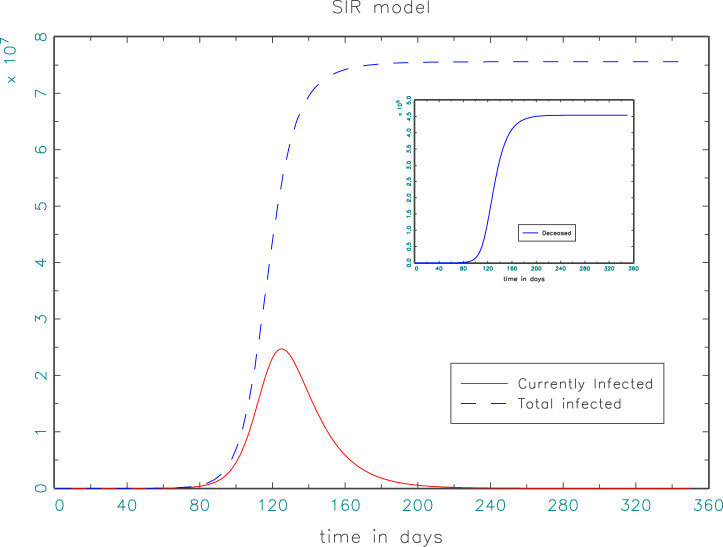
Fig. 1 shows a simulation roughly calibrated for a population of the size of Germany: . We let the infection last for 14 days on average and assume the rate by which an infected person infects others to be , i.e., what is called the reproduction rate (not to be confounded with the number of recovered agents, , in Eqs. 1 through 4 above. Both notations are so common that we adopt them here as well. The respective meaning should be obvious from the context). In the framework of our toy model, this means for each infected person, i.e. she would transmit the virus on average to three other persons during the time of her sickness. Given the average duration, the recovery rate is , and for the death rate we take . Both the infection and death rates are probably rather conservative numbers given the evolving international evidence, cf. Fontanet and Cauchemez [5].
Fig. 1.
Simulation of SIR model showing the evolution of the number of currently infected and the cumulative number of all individuals that have been exposed to the pathogen since the start of the pandemic. The inlet shows the cumulative number of fatalities.
Fig. 1 starts with an initial cluster of five infections at time and shows the simulated outcome over the next 365 days. The total infections show the typical S-shape: After slow beginnings, the pandemic would be in full swing after about four months (with more than 20 million being infected simultaneously at its climax) and would ebb away three months later leaving behind more than 450.000 casualties, most of them happening withing a very short span of a few weeks. As the end of the year, “herd immunity” would be reached given there were lasting protection after exposure (which is still unclear). The notion of “herd immunity” in this context is just a euphemism for letting the disease have its way. In our simulation, about 95 percent of the population gets infected before the epidemic wanes. Note that this large infection rate happens despite the level of what is usually denoted by “herd immunity” being reached at a percentage of of the population. However, the so-defined herd immunity does not imply that the disease vanishes all of a sudden. It only indicates a change from a situation in which every infected individual infects more than one more person to a situation in which less than one additional person gets infected (because the pool of susceptible individuals becomes smaller and smaller). During the final phase without exponential increase, the absolute number of new infections can still be sizable. This is known as the overshoot [cf. 3]. Obviously, additional infections after reaching “herd immunity” are not negligible (a factor apparently widely neglected in current discussions). Despite the simplicity of this simple version of the SIR model, the overall outcome is quite close to that of more detailed models with, e.g. age-specific fatality rates [cf. 6].1
3. The social dynamics of COVID-19
The crucial parameter (at least from a social science perspective) in the system of Eqs. (1) to (4) is or , the reproduction or infection rate. If humans were not aware of the nature of the transmission (as in medieval times), or if an animal population were affected by such a pandemic (like the Usutu virus that affected European blackbirds), the reproduction rate, , would just be a given constant.
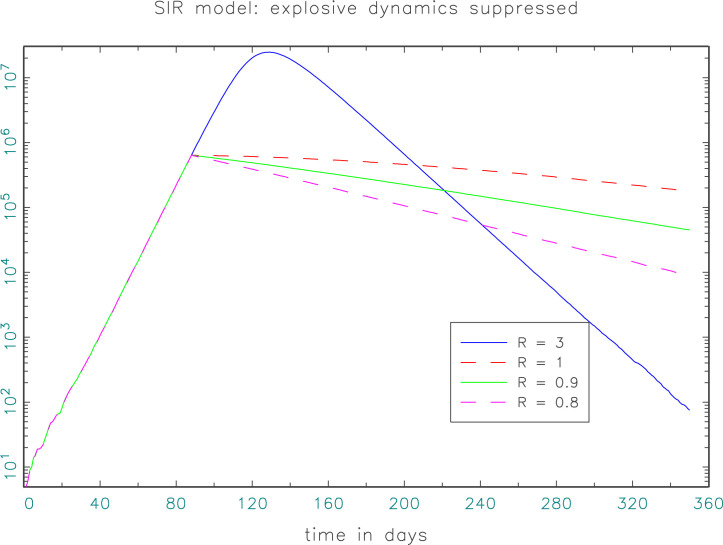
However, humans aware of the above dynamics would be able to control to a certain extent. Within the setting of the model this would be the outcome of all currently pursued strategies of non-pharmaceutical interventions in the form of “social distancing”. Since the only known transmission mechanism is via direct human contact, restricting the frequency of meetings, or reducing the infectiousness of meetings via facial masks or sufficient physical distance, the parameter can in principle be reduced from its “natural” high value to a positive number as close to zero as one wishes. Of course, this comes at a cost, and the costs might depend on factors like population density and the general structure of public life in a society. From a dynamic system perspective, reduction of to a very small number is not even necessary: The above model has a very simple and intuitively plausible bifurcation at . For above this bifurcation value, it would enter into the explosive phase with exponential growth that can be seen in Fig. 1 and that ends eventually with a saturation after a large fraction of the population has been exposed to the virus. For , however, the pandemic ebbs away by itself as illustrated by the broken lines in Fig. 2 in which has been pushed to lower values at the inception of the exponential phase assuming that at the stage when the number of infected individuals reach the number , sudden “social distancing” measures are introduced that reduce to a lower level. Note that even at we observe a very slow decline of new infections which is solely due to the gradual decrease of the number of susceptible persons (as it is the complement of the cumulative number of infections). Of course, our model is the simplest baseline framework for contagion of infectious diseases, but this bifurcation is well-known to survive in more complex and realistic scenarios. One would, then, expect targeted measures of social distancing to strive for a sufficiently low value for a sustainable abatement of the contagion process.
Fig. 2.
Dynamics of new infections with different reproduction rates , assuming “social distancing” measures are imposed, when reaches one million (note the semi-logarithmic scale of the graph).
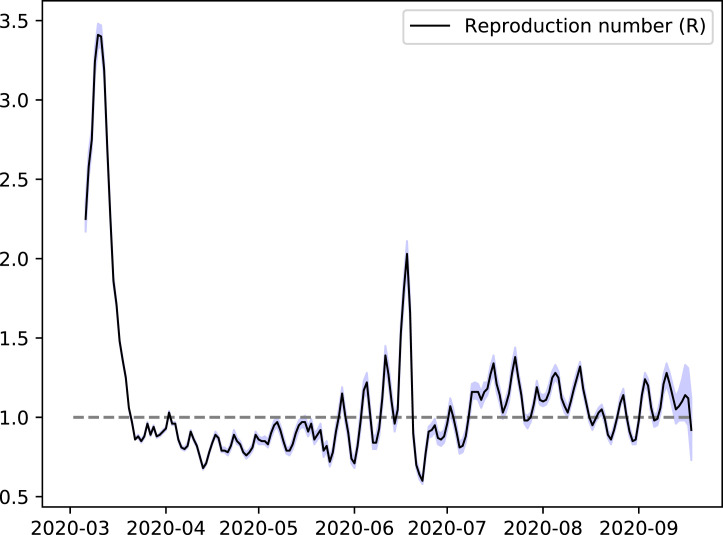
Reproduction rates are also estimated from empirical data, and in many countries are actually regularly published since the inception of the pandemic by national public health authorities. Fig. 3 shows estimates of these numbers as moving averages computed by the German Robert Koch Institute. The perplexing message from this data is that the introduction of social distancing measures in March 2020 has reduced from its high natural level in the vicinity of three, but since this initial reduction hovers about its bifurcation value of unity.
Fig. 3.
The reproduction rate of COVID-19 reported by the German Robert Koch Institute (Germany’s national public health institute). The numbers displayed are 7-day moving averages with elements of nowcasting, i.e., corrections for known delays in reporting and diagnosis.
From a dynamic system perspective, this seems a remarkable outcome: A system that adjusts itself to a bifurcation point at which its dynamics would change qualitatively (from stable convergence to zero infections over time for to unstable explosive dynamics for ). It is hard to imagine that this situation could be a targeted outcome of public health measures as it would constitute a fragile situation in which slight changes of behavior could drive society again back to the disastrous unfolding of the pandemic as it has been illustrated in Fig. 1.
I argue here that this surprising lasting state of the system in the neighborhood of the critical value can be understood as a process of self-organization of society’s handling of the current crisis. In particular, it reflects the piece-meal adaptive adjustments in a non-authoritarian Western country without a sufficiently high basis of scientific penetration of the unfolding pandemic in the broader population or experience with similar epidemic waves.
In the following, I add to Eqs. (1) to (4) a simple behavioral model of agents’ efforts at social distancing inspired by percolation theory from statistical physics (see the authoritative introduction by Stauffer and Sornette [7], and the well-known monograph by Weidlich and Haag [8] for the use of such concepts in the social sciences).
For simplicity, it will be assumed that agents’ choice of following social distancing measures is of binary nature: they either continue their lives in normal mode as before the pandemic or they practice social distancing. How many are practicing social distancing affects the reproduction rate. Let us denote the number of agents practicing social distancing as , and the number of those not following social distancing advice as with
| (5) |
The underlying population is adjusted on the right-hand side by subtracting the deceased for consistency. We define an index of the extent or not of social distancing of the population as:
| (6) |
and assume that the effective reproduction rate can be written as
| (7) |
Obviously, with (normal social interaction) we are back at the natural infection rate whereas complete social distancing obeyed by the entire population would drive down to zero. In reality, the extent of effective social distancing depends on measures imposed by the authorities and relaxations of these measures at certain points in time, and the obedience of the population to the prevailing rules for social distancing. In the absence of a good understanding of the epidemiological principles underlying the dynamic evolution of the contagion process both policy-makers and citizens might rather be driven by a short-sighted adaptive reaction to current numbers of newly infected and deceased persons. For instance, in the German public health debate it had been widely suspected that restrictions had been released too early on the pressure of regional state leaders, a tendency which had been allegedly criticized by chancellor Merkel as an orgy of premature discussions on relaxations (“Öffnungsdiskussionsorgie”, cf. Frankfurter Allgemeine Zeitung of 20 April, 2020).
We combine the tendency of both policy-makers and citizens to inflict and obey social distancing rules by formulating transition rates for agents to move between the groups of followers or non-followers of social distancing:
| (8) |
| (9) |
Short sighted policy-makers/agents without profound understanding of an epidemic dynamic, might just be driven by their perspective of the current situation in terms of reported new infections or fatalities: If the situation appears threatening, more agents would practice social distancing; if the numbers of newly infected and deceased appear relatively small or are going down, many might not take the epidemic serious anymore and would switch back to their normal mode of social interaction. This tendency could be expressed, for instance, by a function in Eq. (8) that is driven by the change over a limited time span of the number of infections and the number of fatalities from the pandemic:
| (10) |
with and parameters for the strength of agents’ reaction to higher rates of infections and deaths, and defining the attention span of agents (and authorities). A steep increase of either infections and fatalities would trigger a high readiness to impose and obey social distancing rules. Vice versa, a seeming decrease of either or both statistics would make agents believe in a return to normal times, so that we could simply hypothesize that
| (11) |
Similar considerations might affect the swiftness by which agents change this behavior, i.e., the parameters and . One could, thus, argue high infections and number of fatalities would increase agents’ awareness of the crisis, hence we could use a similar functional form for :
| (12) |
with and again parameters for the strength of agents’ reactions. is restricted to positive values, as in a situation with decreasing infection and death rates formally non-distancing agents would not perceive the necessity to start with social distancing. For the second parameter we assume that it is constant reflecting a gradual reversal back to normal mode of behavior in the absence of shocking news:
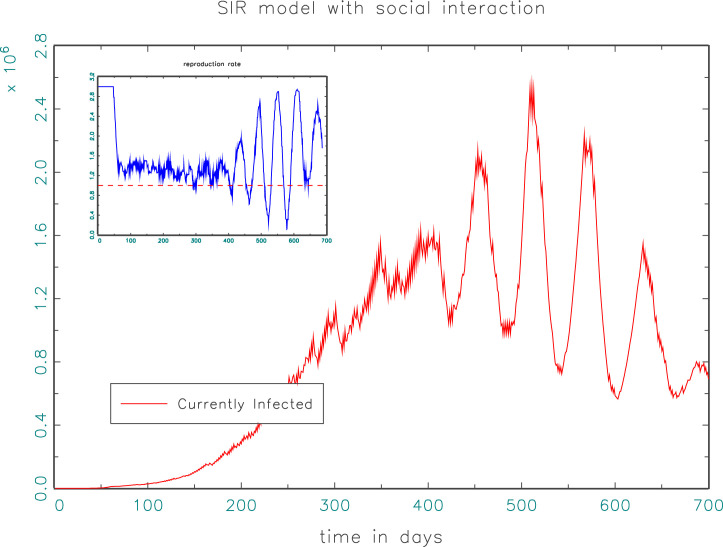
Fig. 4 shows a typical simulation of the extended model consisting of the baseline SIR framework of Eqs. (1) through (4) and the dynamics of social distancing defined in Eqs. (5) through (12). While the main figure exhibits the development of the number of infected persons over more than two years, the inlet shows the effective reproduction number . As can be seen, once the population becomes aware of the development of the pandemic, decreases from its “natural” level of . While this leads first to a stretched out inception phase with some plateaus, at a later stage the trajectory enters into an oscillating mode of repeated relaxations and tightening of restrictions (either by the authorities or through voluntary isolation). The cyclic nature is, of course, an immediate consequence of the limited attention span that has been assumed to govern the behavior of the agents. In the model as it stands, the pandemic would still ebb away after some time as even with the cycles of relaxation and tightening of social distancing eventually the majority of the population would be infected. However, one notes that what would have been over (after apocalyptic unfolding of events) within seven to eight months, is now stretched out over years. If immunity after infection were not lasting, but preserved only for a shorter period (e.g., one year), one could imagine the cyclical dynamics of Fig. 4 to continue ad infinitum since the pool of susceptible individuals would be continuously replenished (a pertinent extension of the model is straight forward).
Fig. 4.
Typical trajectory of a SIR model with social dynamics. The main frame shows the number of infected individuals; the inlet depicts the effective reproduction rate averaged over two weeks. Parameters are: , , , , , and .
Of course, it would appear hard to forecast the changes of human behavior over a prolonged health crisis as the one depicted in Fig. 4. Very likely, repeated waves of increases in infection rates like in this figure would let previous prevention measures look futile so that over time, a more fatalistic attitude might take over. On the other hand, letting the pandemic have its way, will generate the massive losses of lives that have motivated social distancing measures in the first place. How within such a complex scenario events unfold in the long run is probably intimately connected with the social-cultural traditions of each affected country and hard to predict. That changes of behavior make prediction particularly difficult for epidemics of humans has already been recognized prior to COVID-19 [9].
From a dynamic system perspective, the addition of our social dynamics leads to the phenomenon of self-organization of the system in the vicinity of a critical state: The joint dynamics fluctuates around the critical state of the original SIR model at the value of . This is in perfect agreement with the evidence provided for Germany in Fig. 3, and very similar developments seemed to have been going on at least until September in most other European countries.
The above mechanism is similar to what has been denoted sweeping of an instability in statistical physics [e.g. 10]. In this framework, allowing for fluctuations of a control parameter in the vicinity of a bifurcation point provides an alternative to fixing the control parameter exactly at its critical level in order to generate power-law phenomena. Stauffer and Sornette [11] have used random changes of the connectivity parameter of percolation clusters to generate the well-known fat tails of financial returns in a model that interprets the emerging clusters as groups of buyers and sellers in a simple stock market model. In our above setting, the sweeping of the instability is generated by agents’ change of behavior in the face of the unfolding pandemic. There is no self-organization exactly at the critical point , but repeated fluctuations around it driven by a short memory span and a lack of understanding of the biological mechanism and the lack of a strategy for the complete termination of the pandemic. The well-known connection between dynamical systems close to criticality and large fluctuations suggests that this tightrope walk in the vicinity of the critical value could constitute a very fragile trajectory allowing for large eruptions of the pandemic when the critical parameter moves back to the exponential range.
A closely related approach can be found in a recent contribution by Pedro et al. [12] who also model the development of the COVID-19 pandemic as a combined process of a contagious disease and a dynamic process of social behavior in the presence of the unfolding pandemic. Just as in the above model, social distancing in the form of lockdown measures reduce the reproduction rate of a baseline SIR framework for the disease dynamics. In their model, the social costs of the lockdown lead to dwindling political support of the restrictions which are eventually lifted if support within the electorate falls below fifty percent. This in turn triggers a second wave of the pandemic which for many plausible combinations of parameter values of their model turns out to be more severe than the first wave (as it happened indeed in many countries).2
4. Conclusion
This paper has interpreted the current experience with the COVID pandemic in European countries as the outcome of a complex social dynamics interacting with the well-understood epidemiologic dynamics of a standard SIR model. In the absence of vaccines, indeed the only parameter that can explain differences in the evolution in different countries and over time is the social influence on the reproduction parameter . Various measures of “social distancing” , either voluntarily or inflicted by authorities, have obviously reduced the effective reproduction rate in many countries for at least some time to levels close to or below the critical value. It seems puzzling that many countries have not gone further pushing to a level where the pandemic might eventually ebb away. Myopic sequences of relaxations and tightening of measures without a long term perspective appear an obvious candidate to explain these observations. The resulting trajectory tottering along the critical value seems, however, not a sustainable strategy: It seems unlikely that societies could pursue such a trajectory with its agony of social and cultural life for an extended period of time, and it is fragile in so far as an unexpected surge of infections (e.g. an undetected accumulation of cases) could lead to excursions into the exponential regime that are hard to get under control again. Interestingly enough, simulations of the joint dynamics of pandemic and economic evolution have indicated already at an early stage that a policy with a reproduction rate gyrating around would come at higher economic, social and medical costs than more determined and restrictive measures driving the reproduction rate further down [15], [16].
One could also view the sweeping of the instability as a strategy to reach “herd immunity” in the medium run by carefully navigating at a level of moderate pandemic activity. Brett and Rohani [6] show for the UK that a strategy that attempts to reach herd immunity in this way requires an unrealistically long period of fine-tuning of different measures to balance on the tightrope close to the exponential instability. Even if this were feasible, such a strategy would still come with unacceptable levels of fatalities. They conclude that “suppression” would remain the only realistic strategy in the absence of a vaccine. Even if vaccines would become widely available over the year 2021, one still wonders whether a fast and severe suppression would not have come with less hardship than the current scenario of weak mitigation that would have to be stretched until the availability and distribution of a vaccine.
At the time of writing policies of strict suppression have been successful in a number of Asian-Pacific countries (China, Taiwan, Vietnam, Thailand, New Zealand, Australia). Somewhat less rigorous measures (but probably with higher compliance than in Europe) kept the spread of the pandemic at comparatively low levels in Japan and South Korea. While there are not too many communalities in this set of countries besides their regional proximity, their policies demonstrate impressively the potential to curb or completely stop the spread of the COVID pandemic by appropriate measures. While this means avoidance of up to 6 digit numbers of fatalities in large countries, it also in balance has been accomplished with a shorter period of sacrifices and restrictions to public live. In the jargon of economics, one would classify such a policy as achieving a Pareto superior solution. Under this perspective, the major socio-economic puzzle is why European countries find themselves unable to follow these examples. Indeed, following public and political discussions in Europe, such a strict policy appears so alien as not even being considered as a viable alternative, in contrast to its catastrophic opposite, the celebrated “herd-immunity” (i.e., letting the virus have its way).
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
I am grateful to Zhenxi (James) Chen, Frank Westerhoff and two anonymous reviewers for their helpful comments.
The “herd immunity” level in agreement with a cumulative infection rate of two thirds of the population can be spotted easily in Fig. 1 as it is the turning point of the red curve indicating new infections. Obviously the pandemic is not over at this point. If herd immunity exists before a pathogen starts circulating (through vaccination or prior exposure), a pandemic could not take off. But an ongoing pandemic would not immediately stop at the herd immunity threshold.
Alternative ways to formalize social distancing and social interaction in the course of a pandemic include the formalization of memory effects in a SIR model via fractional differentiation [13], or different degrees of isolation within a lattice setting of the geographical arrangement of agents [14].
References
- 1.Moss de Oliveira S., Oliveira P.M.C., Stauffer D. Springer, Berlin; 1999. Evolution, Money, War, and Computers: Non-traditional Applications of Computational Statistical Physics. [Google Scholar]
- 2.Egenter E., Lux T., Stauffer D. Finite-size effects in Monte Carlo simulations of two stock market models. Physica A. 1999;268(1–2):250–256. [Google Scholar]
- 3.Anderson R.M., May R. Oxford University Press; 1991. Infectious Diseases of Humans: Dynamics and Control, vol. 36. [Google Scholar]
- 4.Tolić D., Kleineberg K.-K., Antulov-Fantulin N. Simulating SIR processes on networks using weighted shortest paths. Sci. Rep. 2018;8:1–10. doi: 10.1038/s41598-018-24648-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fontanet A., Cauchemez S. COVID-19 herd immunity: where are we? Nat. Rev. Immunol. 2020;20:583–584. doi: 10.1038/s41577-020-00451-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brett T.S., Rohani P. Transmission dynamics reveal the impracticality of COVID-19 herd immunity strategies. Proc. Natl. Acad. Sci. 2020 doi: 10.1073/pnas.2008087117. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stauffer D., Aharony A. second ed. CRC Press; 1994. Introduction to Percolation Theory; p. 64. [Google Scholar]
- 8.Weidlich W., Haag G. Springer, Berlin; 1983. Concepts and Models of a Quantitative Sociology: The Dynamics of Interacting Populations. [Google Scholar]
- 9.Eksin C., Paarporn K., Weitz J.S. Systematic biases in disease forecasting–The role of behavior change. Epidemics. 2019;27:96–105. doi: 10.1016/j.epidem.2019.02.004. [DOI] [PubMed] [Google Scholar]
- 10.Sornette D. Sweeping of an instability: An alternative to self-organized criticality to get power laws without parameter tuning. J. Physique I. 1994;4(2):209–221. doi: 10.1103/PhysRevLett.72.2306. [DOI] [PubMed] [Google Scholar]
- 11.Stauffer D., Sornette D. Self-organized percolation model for stock market fluctuations. Physica A. 1999;271(3–4):496–506. [Google Scholar]
- 12.Pedro S., Ndjomatchoua F., Jentsch P., Tchuenche M., Anand M., Bauch C. Conditions for second wave of COVID-19 due to interactions between disease dynamics and social processes. Front. Phys. 2020;6 [Google Scholar]
- 13.Saeedian M., Khalighi M., Azimi-Tafreshi N., Jafari G.R., Ausloos M. Memory effects on epidemic evolution: The susceptible-infected-recovered epidemic model. Phys. Rev. E. 2017;95 doi: 10.1103/PhysRevE.95.022409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Contoyiannis Y., Stavrinides S.G., P Hanias M., Kampitakis M., Papadopoulos P., Picos R., M Potirakis S. A universal physics-based model describing COVID-19 dynamics in Europe. Int. J. Environ. Res. Public Health. 2020;17:6525. doi: 10.3390/ijerph17186525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Eichenbaum M.S., Rebelo S., Trabandt M. National Bureau of Economic Research; 2020. The macroeconomics of epidemics. [Google Scholar]
- 16.Dorn F., Khailaie S., Stöckli M., Binder S., Lange B., Vanella P., Wollmershäuser T., Peichl A., Fuest C., Meyer-Hermann M. Das gemeinsame Interesse von Gesundheit und Wirtschaft: Eine Szenarienrechnung zur Eindämmung der Corona-Pandemie. IFO Schnelldienst Digital. 2020;1(6) [Google Scholar]