Mapping Immune Cell Infiltration Using Restricted Diffusion MRI

Abstract

Purpose:

Diffusion MRI provides a non-invasive way to assess tissue microstructure. Based on diffusion MRI, we propose a model-free method called restricted diffusion imaging (RDI) to quantify restricted diffusion and correlate it with cellularity.

Theory and Methods:

An analytical relation between q-space signals and the density of restricted spins was derived to quantify restricted diffusion. A phantom study was conducted to investigate the performance of RDI, and RDI was applied to an animal study to assess immune cell infiltration in myocardial tissues with ischemia-reperfusion injury.

Results:

Our phantom study showed a correlation coefficient of 0.998 between cell density and the restricted diffusion quantified by RDI. The animal study also showed that the high-value regions in RDI matched well with the macrophage infiltration areas in the H&E-stained slides. In comparison with diffusion tensor imaging (DTI), RDI exhibited its outperformance to detect macrophage infiltration and delineate inflammatory myocardium.

Conclusion:

RDI can be used to reveal cell density and detect immune cell infiltration. RDI exhibits better specificity than the diffusivity measurement derived from DTI.

Introduction

Diffusion MRI has been used to probe the characteristics of cellular structures (1). In early diffusion MRI studies, Le Bihan et al. proposed using apparent diffusion coefficient (ADC), a measurement of diffusivity, to quantify water diffusion (2,3). Studies have shown that ADC can be used to evaluate ischemic brain injury (4,5) and cancerous tissues (6,7), and more recent clinical studies have used ADC to reveal the change in cell density in organs with inflammation (8-12). Although ADC is correlated with cellularity, using it to quantify cellularity has limitations. For example, immune cell infiltration can result in a decrease in ADC (13), but the vasogenic edema induced by inflammation can counteract the effect (14). The coexistence of fast and slow diffusion components cannot be readily resolved by ADC because ADC is an ensemble measurement of the overall diffusivity. It is not specific enough to selectively quantity restricted diffusion in the inflammatory tissues (15,16).

Instead of using diffusivity, we propose using the spin density of restricted diffusion to correlate with cellularity. This approach, termed restricted diffusion imaging (RDI), separates non-restricted diffusion from restricted diffusion by their difference in the diffusion displacement. This concept can be realized using q-space imaging (17), a model-free approach that estimates the density of diffusing spins with respect to their diffusion displacement. This feature allows for selective quantification of restricted diffusion while ignoring non-restricted diffusion. Based on q-space imaging, we derived an analytical relation from generalized q-sampling reconstruction (18) to selectively quantify restricted diffusion and obtain RDI.

To examine the performance of RDI, we prepared cell phantoms by embedding different concentrations of rat macrophages in agarose gel. The diffusion MRI was acquired using a stimulated echo sequence with a long diffusion time (80 ms) and multiple samples in diffusion sensitization strength and gradient direction. The diffusion time was set to be long enough for the intracellular water to explore the full volume of the cells (the size of rat macrophages are on the order of 10 μm). We also used an animal study to model the cellularity changes in rat cardiac tissues. We induced an inflammatory response in rat cardiac tissues by transient ligation of the coronary artery (19,20). The transient ligation resulted in ischemia-reperfusion injury (IRI), leading to a localized immune cell infiltration. The performance of RDI was evaluated by comparing it with histopathology slides. We also compared RDI with mean diffusivity calculated from the tensor model to assess their performance in delineating inflammatory myocardium.

Theory

Restricted diffusion imaging

Q-space imaging (17) is a model-free approach that estimates the displacement distribution of diffusing spins. The displacement distribution calculated from q-space imaging, termed ensemble average propagator (EAP), is a three-dimensional probability density function of the diffusion displacement (17). The EAP can be projected on a unit sphere to calculate its corresponding orientation distribution. To simplify the numerical estimation, the calculation of EAP and its projection on a unit sphere can be mathematically combined into one analytical relation (18):

$$\psi (\widehat{\mathbf{u}},L)=L\sum _{\mathbf{q}}W(\mathbf{q})\text{sinc}(2\pi L\mid \mathbf{q}\mid \langle \widehat{\mathbf{q}},\widehat{\mathbf{u}}\rangle )$$ (1)

This equation formulates the relation between the diffusion signals W(q) and the spin distribution function (SDF), $\psi (\widehat{\mathbf{u}},L)$, where $\widehat{\mathbf{u}}$ is a unit vector specifying the direction of the diffusion displacement, and L is a length parameter specifying the upper bound of the diffusion displacement (termed diffusion sampling length). $\psi (\widehat{\mathbf{u}},L)$ estimates the density of spins with diffusion displacement oriented at $\widehat{\mathbf{u}}$ and less than L. ∣q∣ = γGδ/2π, where γ is the gyromagnetic ratio of protons, and G and δ are the strength and the duration of the diffusion-encoding gradient, respectively. $\widehat{\mathbf{q}}$ is a unit vector representing the diffusion gradient direction (i.e., $\widehat{\mathbf{q}}=\frac{\mathbf{q}}{\mid \mathbf{q}\mid }$). $\langle \widehat{\mathbf{q}},\widehat{\mathbf{u}}\rangle$ is the inner product between $\widehat{\mathbf{q}}$ and $\widehat{\mathbf{u}}$.

We can quantify the restricted diffusion, ρ(L), by averaging $\psi (\widehat{\mathbf{u}},L)$ over $\widehat{\mathbf{u}}$ on a unit sphere, where $\widehat{\mathbf{u}}$ is parametrized by the angles, i.e., $\widehat{\mathbf{u}}=(\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta )$:

$$\rho (L)=\frac{1}{4\pi }{\int }_0^{\pi }{\int }_0^{2\pi }\psi (\widehat{\mathbf{u}},L)\text{sin}(\theta )d\varphi d\theta$$ (2)

Without loss of generality, we may set θ as the crossing angle between $\widehat{\mathbf{q}}$ and $\widehat{\mathbf{u}}$ and derive the following analytical expression for ρ(L)(see Appendix for derivation details):

$$\rho (L)=\sum _{\mathbf{q}}\frac{\text{Si}\left(2\pi L\mid \mathbf{q}\mid \right)}{2\pi \mid \mathbf{q}\mid }W(\mathbf{q})$$ (3)

where Si(.) is a sine integral, $\text{Si}(x)\equiv {\int }_0^x\frac{\sin (t)}{t}dt$. If q=0, the term Si(2πL∣q∣)/2π∣q∣ is replaced by L. ρ(L) estimates the density of diffusing spins with diffusion displacements less than L, and it can be used to quantify restricted diffusion. The spatial mapping of ρ(L) is thus termed restricted diffusion imaging (RDI). ρ(L) is a weighted sum of the diffusion weighted signals. The weighting can be pre-computed, and RDI can be calculated by a simple matrix multiplication. Moreover, based on the derivation, ρ(0) is a direct sum of diffusion-weighted signals in the q-space (i.e. $\rho (0)=L\sum _{\mathbf{q}}W(\mathbf{q})$). Thus, the conventional trace-weighted images may be viewed as a partial estimation of ρ(0) using one b-value and three diffusion encoding directions. The derivative of ρ(L), denoted as δ(L), represents the spin density at L:

$$\delta (L)=\sum _{\mathbf{q}}W(\mathbf{q})\mathrm{sinc}\left(2\pi L\mid \mathbf{q}\mid \right)$$ (4)

δ(L) is a nonnegative function by definition, but in practice, q-space imaging has a limited number of q-space acquisition points. The Gibbs phenomenon creates fluctuation, and δ(L) may turn negative at large L. To handle this problem, we set an upper limit to L (denoted as L_max) where δ(L) still remained nonnegative. Our analysis was then limited by L < L_max to avoid this error.

Using L_max, we can use ρ(L_max)–ρ(L) to quantify non-restricted diffusion, $\overline{\rho }(L)$, which is the density of the diffusing spins with diffusion displacement greater than L. The spatial mapping of $\overline{\rho }(L)$ is termed non-restricted diffusion imaging (nRDI), which can be used to investigate various types of tissue edema. The source code for RDI and nRDI is included in DSI Studio (http://dsi-studio.labsolver.org).

Normalization

Both δ(L) and ρ(L) are spin density measurements that quantify restricted diffusion. However, in practice, the spin density estimated here is in arbitrary units. Thus, in our phantom study when we plotted the distribution of δ(L) and ρ(L) with respect to L, we used a local normalization approach setting ρ(L_max)=1 and ${\sum }_{L=0}^{L=L\max }\delta (L)=1$. In our animal study, the δ(L) and ρ(L) estimated at voxel coordinate r can be formulated as δ(r,L) and ρ(r,L), respectively. When we plotted the spatial mapping of δ(L) and ρ(L), we applied a global normalization by setting max_r(ρ(r,L))=1. This global normalization allowed for cross-voxel comparison for RDI.

Optimizing L

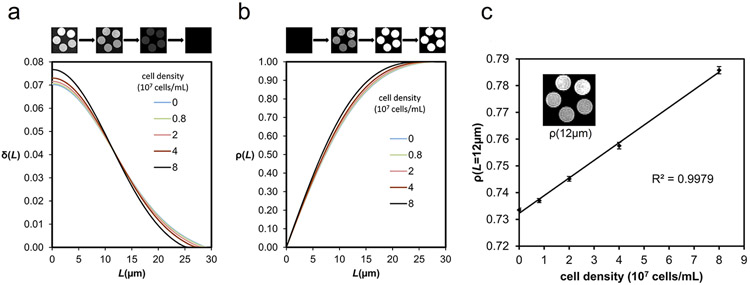
We may choose an L that better discriminates the restricted diffusion induced by cell infiltration from the other non-restricted diffusion. It is noteworthy that the optimal L, denoted as L*, may be different for different diffusion environments. In our phantom experiment, the ρ(L) estimated from a high-cell-density phantom was denoted as ρ_h(L), and the ρ(L) from a low-cell-density phantom was denoted as ρ_l(L). To achieve the best contrast, we would like to maximize the difference between ρ_h(L) and ρ_l(L):

$$L^{\ast }={\text{arg min}}_L\left({\rho }_h(L)-{\rho }_l(L)\right)$$ (5)

The optimized solution can be calculated by setting the derivative of ρ_h(L) - ρ_l(L) to zero and examine whether the optimal solution for L (denoted as L*) results in the maximum difference. The solution can be derived as follows:

$${\delta }_h(L^{\ast })={\delta }_l(L^{\ast })$$ (6)

where δ_h(L) is the derivative of ρ_h(L) and δ_l(L) the derivative of ρ_l(L). Equation 6 indicates that we can plot δ_h(L) and δ_l(L), and their crossing point determines the L* that maximizes the contrast for RDI.

Methods

Phantom study

The rat macrophages were isolated from inbred male Brown Norway rats (Harlan, Indianapolis, IN) and cultured as described in an MRI cell phantom study (21). Phantoms with different cell densities (0.8 x 10⁷, 2 x 10⁷, 4 x 10⁷, and 8 x 10⁷, cells/mL) were prepared by diluting cells in different volumes of 2% agarose gel in shortened 5-mm NMR tubes (Fig. 1a). 4 cell phantoms and one control phantom (2% agarose gel with no cell) were scanned using a Bruker BioSpec 11.7-T scanner (Bruker, Billerica MA). The diffusion acquisition was conducted using a 2D stimulated echo sequence. The b-table was a grid sampling scheme with 101 diffusion encoding gradient directions (22). The b-table is publicly available on the DSI Studio website (http://dsi-studio.labsolver.org). The maximum b-value was 6,000 mm²/sec, diffusion time Δ = 80 ms (i.e., diffusion gradient separation), and the diffusion gradient pulse duration δ = 1 ms. The diffusion weighted images were acquired with TE = 10 ms, TM = 75 ms, TR = 2600 ms. The FOV was 1.26 cm with an in-plane resolution of 0.2 mm and slices thickness of 0.35 mm. ρ(L) and δ(L) were calculated by Equations 3 and 4, respectively, and correlated with the cell density. The data were analyzed using DSI Studio (http://dsi-studio.labsolver.org).

Fig. 1.

(a) The layout of the cell phantoms presented in the cross section. The NMR tubes contain 2% agarose gel with different cell densities. (b) The spatial mapping of δ(L) and ρ(L) shown at L = 0, 10, 20, and 30 μm. δ(L) quantifies the density of diffusing spins with displacement equal to L, whereas ρ(L) quantifies the density of diffusing spins with displacement less than L. The δ(L) images show a decreasing trend with respect to L, and most of the diffusing spins have displacement less than 30 μm. ρ(L) show different contrasts for different cell densities. The best contrast can be achieved at L around 10 μm.

Animal model

We used a rat heart model of IRI (19) to examine whether RDI can reveal the cellularity change due to immune cell infiltration. Inbred male Brown Norway rats (n=6) were used in this experiment. The animal protocols were approved by the Institutional Animal Care and Use Committee of Carnegie Mellon University. All animals received humane care in compliance with the Guide for the Care and Use of Laboratory Animals, published by the National Institutes of Health. IRI was induced by transient ligation of the left anterior descending artery at the mid-level for 45 minutes followed by reperfusion. After 2 days, the heart was harvested and fixed in 4% paraformaldehyde for 24 hrs, followed by storage in phosphate buffer solution at 4 °C for a month. The ex-vivo images were acquired in a short-axis view in a Bruker BioSpec 11.7-T scanner (Bruker, Billerica MA). One of the 6 animals was a sham animal. The sham animal also had transient ligation of the coronary artery, but its MR imaging slices and the histology sections were sampled at myocardium without injury. The diffusion sequences and parameters were identical to the phantom study described above. 25 slices were acquired for each heart sample. T₂-weighted (T2W) images were acquired using a multi-slice multi-echo sequence. TR=1,000 ms, and images acquired with effective echo times of 56 ms were used. The in-plane resolution was 0.1 mm, whereas the slice thickness was 2mm. After the scans, the hearts were sectioned for pathology study.

Pathology preparation and whole slide image recognition

The tissue specimen was embedded in paraffin. For each specimen, two 5-μm tissue sections were taken in a short-axis orientation at the IRI site from the heart tissue and stained with the H&E stain. Immunohistochemistry (IHC) was conducted by using 1:200 anti-rat ED1 monoclonal antibody (AbD SeroTec, Oxford, UK) to label rat macrophages. Peroxidase-conjugate and AEC chromogen (SkyTek Laboratories, Inc., Logan, UT) were used to present brownish-red color on the labeled macrophages on a blue background. The H&E and IHC slides were scanned on a whole slide scanner (Nanozoomer 2.0-HT, Hamamatsu, Japan) to acquire whole slide images at 20x magnification. The whole slide image data were processed by an automated analysis method (23) implemented in WS-Recognizer, which is public available at http://ws-recognizer.labsolver.org. The cell density was obtained by recognizing all cell nuclei in the H&E-stained slides, whereas region with hemorrhagic necrosis was identified by recognizing the red blood cells. These spatial distribution mappings were used as the ground truth to examine the performance of RDI. To match the pathology images with the diffusion MRI slices, we compared them manually using the interface provided by DSI Studio and selected the MRI slices that best matched with the pathology sections.

Results

Phantom study

We analyzed the phantom data and visualized δ(L) and ρ(L) by setting the maximum value as one (i.e., max_r δ(r, L)=1 and max_r ρ(r, L)=1), as shown in Fig. 1b. δ(L) quantifies restricted diffusion with displacement equal to L, whereas ρ(L) quantifies restricted diffusion with displacement less than L. The cross section of the cell phantom is presented at L = 0, 10, 20, and 30 μm. At L = 0 μm, the cell phantom with the highest cell density (8 x 10⁷ cells/mL) shows the highest value in δ(L). At L = 10 and 20 μm, there is no obvious difference in δ(L) between the cell phantoms. At 30 μm, there is no visible signals in δ(L), suggesting that the diffusion displacement of the spins is mostly less than 30 μm. On the other hand, ρ(L) shows different contrasts at different L values, and the best contrast can be observed at ρ(10 μm) in Fig. 1b. This supports our claim that the contrast in ρ(L) can be optimized by choosing a suitable L, as formulated by Eq. (5) and (6).

Since each cell phantom contained around 5000 voxels in the diffusion-weighted images, we averaged their values and carried out a normalization by setting ${\sum }_{L=0}^{L=L\max }\delta (L)=1$ and ρ(L_max)=1. The averaged values of δ(L) and ρ(L) are plotted in Fig. 2a and 2b, respectively. As shown in Fig. 2a, the increase of the cell density results in an increase of δ(L) from L = 0 to 12 μm. The crossing of the curves at 12 μm suggests that the difference in ρ(L) is maximized at L = 12 μm (according to Eq. 6), and we can set L* = 12 μm as an optimal value to maximize the contrast in ρ(L). Figure 2c shows a correlation analysis between the cell density and ρ(L*), and the error bar shows the standard error of the mean. The results show a correlation coefficient of 0.99895, suggesting that ρ(L*) correlates well with the cell density. We also conducted a tensor-based analysis on the same phantom data as a comparison. The mean diffusivity map plotted in Fig.3a shows lower diffusivities in phantoms with higher cell densities. The correlation analysis between diffusivity and cell density shows a strong negative trend with a correlation coefficient of −0.95432 (Fig. 3b). The drop of diffusivity in high cell density phantoms is substantial and thus allows for detecting immune cell infiltration. In comparison, RDI is positively correlated with cell density, and the increase of restricted diffusion may indicate immune cell infiltration.

Fig. 2.

(a) The distribution curves of δ(L) form a crossing at 12 μm. This suggests that an L of 12 μm can achieve the best differentiation power in ρ(L). (b) The distribution of ρ(L) shows a maximum difference at 12 μm. (c) The regression line shows the correlation between the cell density and ρ(12 μm) of the cell phantoms. The correlation analysis shows a high correlation coefficient of 0.998.

Fig. 3.

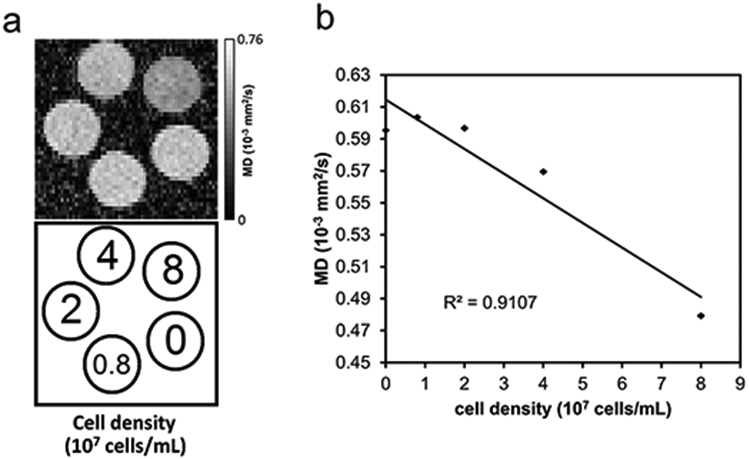
The mean diffusivity of the cell phantom. (a) The mean diffusivity decreases in phantoms with higher cell densities. (b) The mean diffusivity is negatively correlated with cell density, suggesting that diffusivity can be used to detect cell infiltration.

Animal study

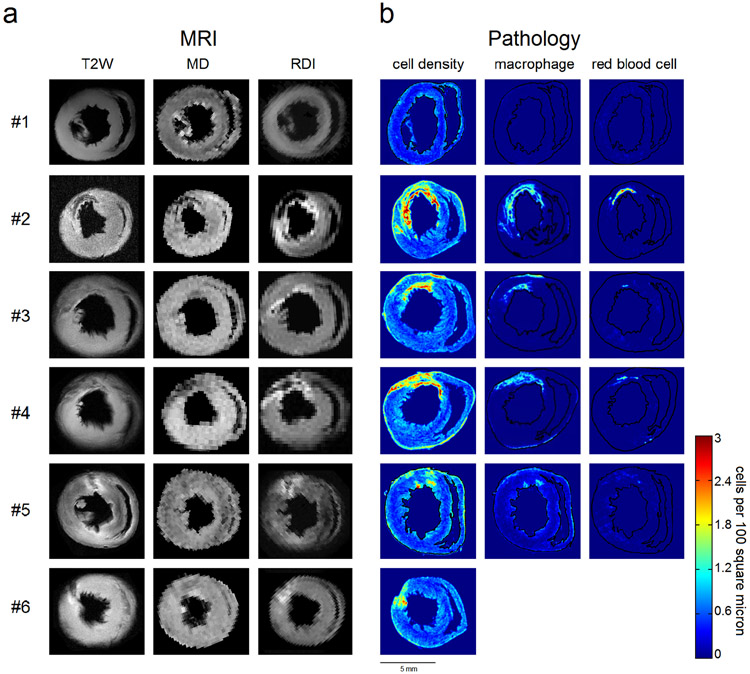
We further compared RDI with T2W images and mean diffusivity (MD) maps (Fig. 4). The ρ(L*) mapping was calculated using L* = 12 μm, an optimal value obtained from the phantom study. The mean diffusivity was calculated by fitting the diffusion data with a diffusion tensor model, and a tissue mask was used to remove background noise. Figure 4a shows the T2W, MD, and RDI (i.e., the ρ(L*) values) mapping, whereas the cell density, macrophage distribution, and red blood cell distribution calculated from the histopathology slides are shown in Figure 4b. T2W images have been widely used to detect tissue edema and area at risk, whereas MD has been shown to be negatively correlated with cell density. The bright regions in the T2W images can be due to increased water content (e.g., edema), whereas the dark regions can be due to hemorrhage. On the other hand, a high-value region in MD can be due to vasogenic edema or tissue breakdown, whereas a low-value region in MD can be due to cytotoxic edema or hemorrhage. The cell density in Fig. 4b was obtained by whole slide image analysis (23), an automatic approach to recognize cell nuclei in the H&E-stained slides. The red blood cells were recognized in the H&E stained slides using the same approach, and its spatial distribution indicates hemorrhagic necrosis. The macrophage distribution was obtained from slides stained by IHC to label ED1⁺ macrophages. The macrophages were automatically recognized by the same automated whole slide image analysis to reveal its spatial distribution. The images from different modalities are manually rotated so that the right ventricle is positioned to the right.

Fig. 4.

A comparison between T₂-wighted imaging (T2W), mean diffusivity (MD), restricted diffusion imaging (RDI), and histopathological quantification of cell density, macrophage, and red blood cell. A total of 6 animals, including one sham animal (#1), are presented, and each row corresponds to the same animal specimen. The high-value regions in T2W images indicate tissue edema, whereas the low-value regions are due to hemorrhagic necrosis. . The decreased values in MD may be due to the restricted diffusion caused by inflammation, but the contrast is not good enough to delineate the inflammatory regions because hemorrhagic necrosis also causes decreased values in the MD map. By contrast, RDI shows a pattern consistent with the cell density obtained from histopathological quantification. The high-value regions match well with the high cell density regions, and the low-value region matches well with hemorrhagic necrosis.

Each row of the inset figures in Fig. 4 corresponds to the same heart specimen of an animal. A total of 6 animal hearts are shown in the figure, whereas animal #1 is the sham animal. The myocardium of the sham animal (#1) presents homogeneous intensity in the T2W image and RDI map, whereas the MD map has prominent noise at the tissue interface due to partial volume effect. The image presentation of the sham animal is substantially different from that of the myocardium with IRI (animals #2~#6).

The T2W images in Fig. 4a show a prominent drop of intensity at the hemorrhagic myocardium. For example, the dark region in the T2W images (9-12 o’clock in animal #2, 11-12 o’clock in animal #5 and 9-10 o’clock in animal #6) matches well with the red blood cell distribution. and mild increase of intensity at the inflammatory myocardium (e.g. 11-12 o’clock in animals #5 and 9-10 o’clock in animal #6). The high-value regions in T2W images reveal injured myocardium with tissue edema that suggests “area at risk”. However, the inflammatory regions revealed by histopathology appear larger than the high-value regions shown by the T2W images (e.g., 11-12 o’clock in animals #2 and 11-12 o’clock in #3). It is possible that T2W images may underestimate area at risk at the early stage of ischemic injury.

The low-value regions in MD map in Fig. 4a indicate immune cell infiltration (10-12 o’clock in animal #2, 9-12 o’clock in animal #4); however, hemorrhagic necrosis also creates low MD values at the same regions. Consequently, MD cannot effectively differentiate area at risk from hemorrhagic necrosis (e.g., the low-value region in animal #4). In general, the contrast in the MD map is not specific enough to delineate the inflammatory regions that can be salvaged from ischemic injury. In comparison, RDI in Fig. 4a presents a pattern consistent with the cell density distribution shown in the H&E-stained slides. The high-value regions in RDI (9-12 o’clock in animals #2, #3, #4, #5, and #6) correspond well with the high cell density areas in the H&E-stained slides, whereas the low-value regions in RDI (9-12 o’clock in animals #2, #4, and #5) match well with the hemorrhagic necrosis region. In general, the contrast pattern of RDI clearly delineates myocardium with immune cell infiltration.

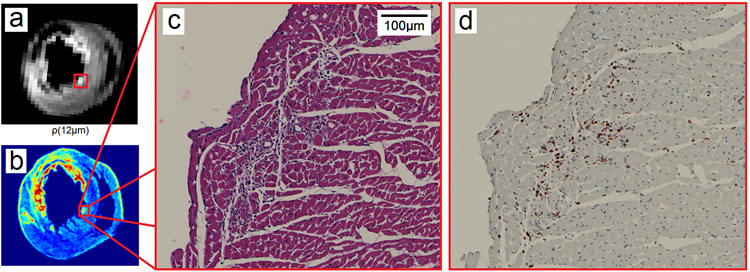
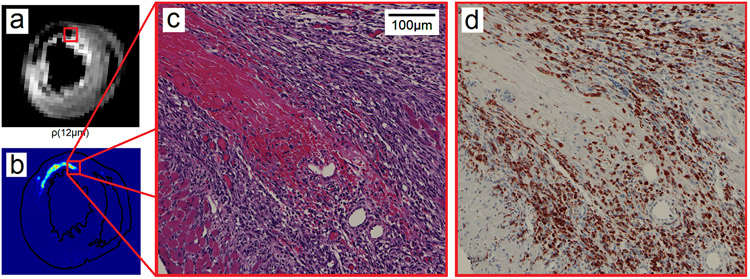
Using animal #2 as an example, Figure 5 illustrates a hot spot (red rectangle) in RDI and its corresponding histopathology images. Figure 5a shows the ρ(L*) mapping whereas Fig. 5b shows the cell density in the H&E slide. The red rectangle in Figs. 5a and 5b indicates a hot spot with increased cell density. This hot spot is further illustrated by its corresponding H&E image (Fig. 5c) and IHC image (Fig. 5d). The H&E image shows prominent cell infiltration in the myocardium, and the IHC image further confirms that the cells are ED1⁺ macrophages. These results suggest that RDI is sensitive to the immune cell infiltration in a rat IRI model. Figure 6 shows a region with a hemorrhagic necrosis core (red rectangle) in RDI and illustrates its corresponding histopathology images. Figure 6a shows the ρ(L*) mapping, whereas Fig. 6b shows the distribution of red blood cells in the H&E slide. The red rectangle in Figs. 6a and 6b indicates a region with hemorrhagic necrosis, which is further illustrated by its corresponding H&E image (Fig. 6c) and IHC image (Fig. 6d). The H&E image shows hemorrhagic necrosis with cell infiltration at the perimeter, and the IHC image further confirms that the cells are ED1⁺ macrophages. As shown by these figures, ρ(L*) presents a high-value region indicating immune cell infiltration and a low-value region indicating hemorrhagic necrosis. This feature enables effective differentiation between immune cell infiltration and hemorrhagic necrosis.

Fig. 5.

The high-value regions in the ρ(L*) mapping match well with the cell infiltration regions shown in the histopathology images. (a) The ρ(L*) mapping shows a high-value region in a rat heart with ischemia-reperfusion injury. (b) The cell density calculated from the H&E-stained image shows high cellularity in the same region. (c) The H&E image at the region shows prominent cell infiltration. (d) The IHC image confirms that the cells are ED1⁺ macrophages.

Fig. 6.

The low-value regions in the ρ(L*) mapping match well with the hemorrhagic necrosis regions in the histopathology slide. (a) The ρ(L*) mapping shows a low-value region in a rat heart with ischemia-reperfusion injury. (b) The red blood cell distribution in the H&E-stained suggests hemorrhagic necrosis in the same region. (c) The H&E image of the region shows prominent hemorrhagic necrosis with cell infiltration at the perimeter. (d) The IHC image confirms that the infiltrating cells are ED1⁺ macrophages. RDI can differentiate immune cell infiltration from hemorrhagic necrosis.

Using animal #4 as an example, we show the spatial mapping of ρ(L) at L=3, 6, 9, 12, 15, and 18 μm in Fig. 7. All inset figures are shown by the same contrast to facilitate comparison. A small L results in low values in ρ(L) for both normal and inflammatory myocardium, whereas larger Ls result in high values in ρ(L). An optimal value at 12 μm provides a good contrast to differentiate inflammatory myocardium from the normal myocardium.

Fig. 7.

The spatial mapping of ρ(L) with L = 3, 6, 9, 12, 15, and 18 μm. Different Ls result in different contrasts in ρ(L). This allows us to observe the restricted diffusion with respect to different diffusion displacement.

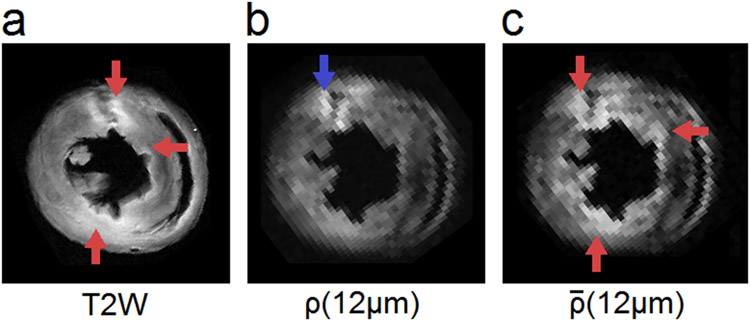
We further use animal #5 as an example to illustrate non-restricted diffusion imaging (the $\overline{\rho }(L)$ mapping, Fig. 8c) in comparison with the T2W image (Fig. 8a) and RDI (Fig. 8b). Animal #5 has obvious edematous myocardium as shown by the bright regions in the T2W image (red arrows in Fig. 8a). The restricted diffusion quantified by ρ(L*) shows only the region with increased cell density (the blue arrow in Fig. 8b), whereas non-restricted diffusion quantified by $\overline{\rho }(L^{\ast })$ (Fig. 8c) enhances edematous myocardium (red arrows in Fig. 8c), which has increased non-restricted diffusion. RDI and nRDI together provide complementary information that can differentiate two pathological conditions. The first condition is edematous myocardium without prominent immune cell infiltration. This condition may occur in the early stage of myocardial injury before immune cell infiltration. The second condition is inflammatory myocardium with substantial cell infiltrations and tissue edema. This condition indicates a more developed stage of myocardial injury that may have irreversible damage to the myocardium.

Fig. 8.

(a) T2W imaging and (b) restricted diffusion imaging compared with (c) non-restricted diffusion imaging. The restricted diffusion reveals a region with immune cell infiltration (blue arrow), whereas the non-restricted diffusion reveals regions with tissue edema (red arrows). Non-restricted diffusion allows for mapping of the edematous myocardium and provides complementary information in addition to the findings in the T2W image.

Discussion

We propose RDI as a new approach to quantify restricted diffusion and to correlate it with cell density. Our experiment showed that RDI is highly correlated with cell density and can be used to reveal immune cell infiltration. In our phantom study, the optimized restricted diffusion, ρ(L*), showed a high correlation coefficient with cell density (correlation coefficient = 0.998). In our ex-vivo animal study, the immune cells infiltration and hemorrhagic necrosis revealed by RDI matched well with the finding in the H&E slides. In comparison, the MD map presented a slightly decrease of value for immune cell infiltration and failed to delineate inflammatory myocardium from hemorrhagic necrosis. The results of this study support our claim that RDI can provide a more sensitive and specific index for detecting changes in cell density.

Several model-based methods have been proposed to quantify restricted diffusion, including the composite hindered and restricted model (24), diffusion based spectrum imaging (16), and the restricted spectrum imaging (25). In comparison, these methods were based on axonal models and did not explicitly specify the length of diffusion displacements, which is critical for quantifying restricted diffusion. The composite hindered and restricted model required numerical fitting of a composite diffusion model. Diffusion basis spectrum imaging required fitting data to a complex multiple-tensor model. Restricted spectrum imaging used a linear mixture model of diffusion components and categorized diffusion into restricted and hindered diffusion. The computation required complicated numerical estimation, including spherical harmonic decomposition, constrained minimization, and regularization. Due to the limitation of overfitting, it is challenging for these model-based methods to calculate a “domain” of diffusion measurement that allows for selective quantification of restricted diffusion. By contrast, RDI is a model-less approach that makes use of q-space imaging to estimate the density of diffusion spins with respect to their diffusion displacement. This enables RDI to quantify restricted diffusion given an arbitrary diffusion displacement. Moreover, the calculation does not rely on an underlying diffusion model (e.g. tensor model, axonal models). It can be computed by a simple weighted sum of diffusion-weighted images and does not require a complicated numerical optimization to estimate the model parameters. By adjusting the length parameter L, RDI further allows for specifying the diffusion displacement to adjust its sensitivity and specificity to different diffusion environments.

There is also a novelty in our pathology approach. We applied an automated whole slide image analysis method (23) to the H&E slides to obtain the cell density and the distribution of hemorrhagic necrosis. The recognition was fully automated, and the analysis covered all fields of view in the slides, thereby minimizing possible human errors. The cell density obtained from automated whole slide image analysis enabled an objective quantification of pathology information and provided a direct comparison to validate our results.

The IRI model simulates the reperfusion injury of infarcted myocardium after thrombolytic therapy or surgical intervention. Although acute myocardial infarction (AMI) and IRI are both induced by ischemic injury, their image presentation can be substantially different. At the early stage of reperfusion, the inflammatory myocardium still has intact structure and presents limited edema or tissue breakdown. This is also demonstrated in our histology images (Fig. 5). More importantly, studies have indicated the critical role of immune cells in IRI (26-29), and thus, an imaging approach capable of revealing early immune cell infiltration may greatly assist evaluation of treatment response and prognosis. To this end, diffusivity-based measurements seemed to be a good index to evaluate inflammatory myocardium. However, in myocardium with IRI, it is possible that non-restricted diffusion (e.g., due to vasogenic edema) and restricted diffusion (e.g., due to immune cell infiltration or cytotoxic edema) coexist. Depending on the disease course, the overall diffusivity may appear either decreased (if dominated by cell infiltration) or increased (if dominated by edema). Consequently, the diffusivity map may not be effective in delineating the inflammatory regions if the restricted and non-restricted diffusion cancel with each other. By contrast, RDI can decouple the restricted diffusion from non-restricted diffusion, allowing for enhancing the existence of immune cell infiltration. This makes an early assessment of local inflammation possible and may assist further clinical decision on the usage of immunosuppressant after myocardial reperfusion (29).

Studies have also used diffusion tensor imaging to access the remodeling of myocardium after infarction (30-34). While diffusivity and helix angle can be used to evaluate the remodeling process of AMI, RDI can serve as a complementary approach to evaluate inflammation at the early stage. A combination of conventional diffusion study and RDI may enable a full investigation of ischemic injury and allows for early intervention to salvage myocardium. Similarly, numerous studies have demonstrated the value of T2W imaging to access area at risk (35-38) because it is sensitive to edema. However, our animal study showed that the tissue inflammation can involve a larger area than the high-value regions shown in the T2W images. It is possible that the area at risk revealed by T2W imaging may be underestimated due to the fact that reversible injury may have limited edema and thus may not be readily discernible in T2W images until the edema is fully developed (39). In such a condition, RDI can play a complementary role by detecting the immune cell infiltration and allows for early medical evaluation.

There are limitations in this study. The increase of restricted diffusion can be attributed to many sources, not necessarily due to macrophage infiltration. A cell-specific approach is using iron-oxide particles to selectively label immune cells (40). Moreover, our ex-vivo study adopted a case presentation approach and used only a small number of animals. We only did a manual matching between the diffusion MRI and histopathology images because the tissue specimen had substantial deformation after fixation. The resolution difference also jeopardized automatic registration. Consequently, our RDI did not match perfectly with the pathology images. In addition, the diffusion characteristics (e.g., diffusivity) change dramatically after tissue fixation, and we did not acquire in-vivo diffusion MRI of the rat hearts. This limitation is due to the fact that rat hearts beat much faster than the human hearts, making in-vivo diffusion imaging more challenging. Nonetheless, studies have used stimulated echo sequences to acquire cardiac diffusion imaging in human subjects (30,41-45), and thus, technically RDI is feasible for clinical applications to study area at risk in ischemic heart diseases. In addition to cardiac imaging, RDI and nRDI can also be applied to brain imaging; however, whether they are able to detect cellularity change due to tumors or inflammation requires further investigation.

Conclusion

RDI is a model-free approach to quantify restricted diffusion and to reveal changes in cell density. The high-value regions in RDI are specific to the increase of cell density, allowing it to provide accurate delineation of the inflammatory tissues and lead to better diagnostic and prognostic evaluation.

Appendix

In this appendix, we show the derivations for Eq. (3) and (4).

First, Eq. (1) and (2) can be combined as follows:

$$\begin{gathered} \rho (L)=\frac{L}{4\pi }{\int }_0^{\pi }{\int }_0^{2\pi }\sum _{\mathbf{q}}W(\mathbf{q})\mathrm{sinc}\left(2\pi L\mid \mathbf{q}\mid \langle \widehat{\mathbf{q}},\widehat{\mathbf{u}}\rangle \right)\sin (\theta )d\varphi d\theta \\ =\frac{L}{4\pi }\sum _{\mathbf{q}}W(\mathbf{q}){\int }_0^{\pi }{\int }_0^{2\pi }\mathrm{sinc}\left(2\pi L\mid \mathbf{q}\mid \langle \widehat{\mathbf{q}},\widehat{\mathbf{u}}\rangle \right)\sin (\theta )d\varphi d\theta \end{gathered}$$ (A.1)

Without loss of generality, we may set θ as the crossing angle between $\widehat{\mathbf{q}}$ and $\widehat{\mathbf{u}}$ (i.e. $\langle \widehat{\mathbf{q}},\widehat{\mathbf{u}}\rangle =\cos (\theta )$). Thus, we have the following equation:

$$\rho (L)=\frac{L}{4\pi }\sum _{\mathbf{q}}W(\mathbf{q}){\int }_0^{\pi }{\int }_0^{2\pi }\mathrm{sinc}\left(2\pi L\mid \mathbf{q}\mid \cos (\theta )\right)\sin (\theta )d\varphi d\theta$$ (A.2)

Then we integrate the function with respect to ϕ and θ:

$$\begin{gathered} \rho (L)=\frac{L}{2}\sum _{\mathbf{q}}W(\mathbf{q}){\int }_0^{\pi }\mathrm{sinc}\left(2\pi L\mid \mathbf{q}\mid \cos (\theta )\right)\sin (\theta )d\theta \\ =\frac{1}{2}\sum _{\mathbf{q}}\frac{W(\mathbf{q})}{2\pi \mid \mathbf{q}\mid }\text{Si}{\left(2\pi L\mid \mathbf{q}\mid \cos (\theta )\right)\mid }_{\theta =0}^{\theta =\pi } \end{gathered}$$ (A.3)

where Si(.) is a sine integral, $\text{Si}(x)\equiv {\int }_0^x\frac{\sin (t)}{t}dt$.

$$\begin{gathered} \rho (L)=\frac{1}{2}\sum _{\mathbf{q}}\frac{W(\mathbf{q})}{2\pi \mid \mathbf{q}\mid }\left(\text{Si}\left(-2\pi L\mid \mathbf{q}\mid \right)-\text{Si}\left(2\pi L\mid \mathbf{q}\mid \right)\right) \\ =\sum _{\mathbf{q}}\frac{W(\mathbf{q})}{2\pi \mid \mathbf{q}\mid }\text{Si}\left(2\pi L\mid \mathbf{q}\mid \right) \end{gathered}$$ (A.4)

The derivative of ρ(L) can be derived as follows:

$$\begin{gathered} \frac{d\rho (L)}{dL}=\sum _{\mathbf{q}}\frac{W(\mathbf{q})}{2\pi \mid \mathbf{q}\mid }\frac{d\text{Si}\left(2\pi L\mid \mathbf{q}\mid \right)}{dL} \\ =\sum _{\mathbf{q}}W(\mathbf{q})\text{sinc}(2\pi L\mid \mathbf{q}\mid ) \end{gathered}$$ (A.5)