Phasic cholinergic signaling promotes emergence of local gamma rhythms in excitatory–inhibitory networks

Abstract

Recent experimental results have shown that the detection of cues in behavioral attention tasks relies on transient increases of acetylcholine (ACh) release in frontal cortex and cholinergically driven oscillatory activity in the gamma frequency band (Howe et al. Journal of Neuroscience, 2017, 37, 3215). The cue-induced gamma rhythmic activity requires stimulation of M1 muscarinic receptors. Using biophysical computational modeling, we show that a network of excitatory (E) and inhibitory (I) neurons that initially displays asynchronous firing can generate transient gamma oscillatory activity in response to simulated brief pulses of ACh. ACh effects are simulated as transient modulation of the conductance of an M-type K⁺ current which is blocked by activation of muscarinic receptors and has significant effects on neuronal excitability. The ACh-induced effects on the M current conductance, g_Ks, change network dynamics to promote the emergence of network gamma rhythmicity through a Pyramidal-Interneuronal Network Gamma mechanism. Depending on connectivity strengths between and among E and I cells, gamma activity decays with the simulated g_Ks transient modulation or is sustained in the network after the g_Ks transient has completely dissipated. We investigated the sensitivity of the emergent gamma activity to synaptic strengths, external noise and simulated levels of g_Ks modulation. To address recent experimental findings that cholinergic signaling is likely spatially focused and dynamic, we show that localized g_Ks modulation can induce transient changes of cellular excitability in local subnetworks, subsequently causing population-specific gamma oscillations. These results highlight dynamical mechanisms underlying localization of ACh-driven responses and suggest that spatially localized, cholinergically induced gamma may contribute to selectivity in the processing of competing external stimuli, as occurs in attentional tasks.

1 ∣. INTRODUCTION

Cholinergic neurons situated in the basal forebrain (BF) project to virtually all cortical layers and regions. In contrast to traditional descriptions of this projection system as “diffusely organized” and involved in the relatively slow regulation of cortical activity states, contemporary evidence indicates the presence of BF subpopulations of neurons with highly topographically organized afferent and efferent projections (Gielow & Zaborszky, 2017; Yuan, Biswal, & Zaborszky, 2018; Zaborszky, Buhl, Pobalashingham, Bjaalie, & Nadasdy, 2005; Zaborszky et al., 2015) and, in cortex, of spatially and temporally discrete, fast, phasic or “transient” cholinergic signaling (Parikh, Kozak, Martinez, & Sarter, 2007). Because cortical cholinergic activity is necessary for attentional performance in rodents and humans (Kim, Muller, Bohnen, Sarter, & Lustig, 2019; McGaughy, Kaiser, & Sarter, 1996), the role of cholinergic transients has been investigated specifically in the context of attentional performance. In rats performing a signal detection-based attention task, cholinergic transients were found to be evoked by cues that were successfully detected, but not by missed cues (Howe et al., 2013). Moreover, optogenetic suppression and generation of transients indicated that cholinergic transients are necessary and sufficient for the detection of cues in such contexts (Gritton et al., 2016). Transient cholinergic signaling has been proposed to account for a range of behavioral and cognitive functions which traditionally have been associated with more slowly (over minutes) changing extracellular ACh levels (Sarter & Lustig, 2020).

Consistent with the finding that cholinergic transients are necessary to force a relatively complex behavioral response, the determination of their post-synaptic impact indicated that these transients generate high-frequency oscillations in the gamma range in frontal cortex and that gamma oscillations remain active through the cue-response period. Moreover, generation of gamma oscillations requires local, frontal stimulation of muscarinic M1 ACh receptors (mAChRs). Blocking M1-mediated increases in gamma power was sufficient to reduce cue detection rates (Howe et al., 2017). The present study was guided by questions about the potential, neuronal network-based mechanisms which allow brief, phasic ACh release events to generate such impactful high-frequency oscillations.

Using biophysical models of networks of excitatory and inhibitory neurons, we show that simulated transient ACh modulation through mAChRs can induce network gamma rhythmicity. As previously shown (Borgers, Epstein, & Kopell, 2005) (Tiesinga, Fellous, Jose, & Sejnowski, 2001), simulated mAChR effects on membrane potassium currents can promote tonic synchronous network oscillatory activity in the gamma band through a Pyramidal-Interneuronal Network Gamma (PING) mechanism. While these previous results suggest that transient ACh modulation should be able to result in transient gamma-band oscillatory activity, many questions remain regarding network and modulation conditions that support reliable generation and dissolution of transient gamma rhythmic activity. In this study, we particularly focus on the characteristics of transient ACh modulation and network properties that allow the transient emergence of gamma oscillations from background asynchronous, non-rhythmic activity. The role of acetylcholine in attentional modulation of neural network responses has been previously investigated in computational models of diverse brain networks (Borgers et al., 2005; Borgers & Kopell, 2008; Deco & Thiele, 2011; Hasselmo, Anderson, & Bower, 1992; Tiesinga et al., 2001) (see Newman, Gupta, Climer, Monaghan, and Hasselmo (2012) and Thiele and Bellgrove (2018) for reviews). Here, we concentrate on ACh-induced effects on neuronal excitability that generate transient gamma-band rhythmicity that is associated with attentional performance. We show that spatially localized transient ACh modulation can induce spatially localized transient gamma oscillations which can act as a substrate for attentional selectivity in network processing of external stimuli. However, we also show that the parametric region in which gamma oscillations are readily generated due to ACh increase is bistable. This means that reduction of ACh tone alone may not lead to its abolition—noise or other desynchronizing agents are needed for prompt gamma dissolution.

2 ∣. METHODS

2.1 ∣. Neuron model

All neurons in the network are modeled using a Hodgkin–Huxley-type model that includes a Na+ current, a delayed rectifier K⁺ current and a leak current. An additional M-type slow K⁺ current is added to simulate modulation by acetylcholine via mAChRs (Krnjevic, 2004; McCormick & Prince, 1985; Stiefel, Gutkin, & Sejnowski, 2009). The maximum conductance g_Ks of the M-type K⁺ current is the parameter that represents the amount of ACh modulation. In general, g_Ks is set between 0 and 1.5 mS/cm² with low g_Ks corresponding to large concentration of ACh. The current balance equation for each neuron is

$$\begin{gathered} C\frac{dV}{dt}=-g_{\text{Na}}{m}_{\infty }^{3}h\left(V-E_{\text{Na}}\right)-g_{\text{Kd}}{n}^4\left(V-E_{\mathrm{K}}\right)-g_{\text{Ks}}z\left(V-E_{\mathrm{K}}\right) \\ -g_{\mathrm{L}}\left(V-E_{\mathrm{L}}\right)+I_{\text{app}}+I_{\text{noise}}-I_{\text{syn}} \end{gathered}$$

where C = 1μF/cm². V represents the membrane voltage in millivolts, and t is time in milliseconds. g_Na, g_Kd, g_Ks and g_L are maximal conductances of the corresponding currents. In all the cells, g_Na = 24 mS/cm², g_Kd = 3 mS/cm², and g_L = 0.02 mS/cm². g_Ks is varied as described below. To show the influence of g_Ks on neuronal excitability, the neuronal input–frequency curve is plotted for various values of g_Ks (Figure 1c). The E_Na, E_K and E_L are the reversal potentials for sodium, potassium and leak currents, where E_Na = 55 mV, E_K = −90 mV, and E_L = −60mV, respectively. I_app represents the externally applied current to both excitatory and inhibitory cells. I_syn models the synaptic input current that the cell receives from all other connected cells in the network (see below). I_noise represents external Poisson noise delivered to each cell (see below). The m_∞, h, n and z are unitless gating variables of the corresponding current activation, with their evolution given by general equation:

$$\frac{dX}{dt}=\frac{X_{\infty }(V)-X}{{\tau }_X(V)}\text{for}X=h,n,z$$

where

$$\begin{gathered} m_{\infty }(V)=\frac{1}{1+e^{(-V-30)∕9.5}} \\ {h}_{\infty }(V)=\frac{1}{1+e^{(V+53)∕7.0}} \\ {n}_{\infty }(V)=\frac{1}{1+e^{(-V-30)∕10}} \\ {z}_{\infty }(V)=\frac{1}{1+e^{(-V-39)∕5}} \\ {\tau }_h(V)=0.37+\frac{2.78}{1+e^{(V+40.5)∕6}} \\ {\tau }_n(V)=0.37+\frac{1.85}{1+e^{(V+27)∕15}} \\ {\tau }_z(V)=75. \end{gathered}$$

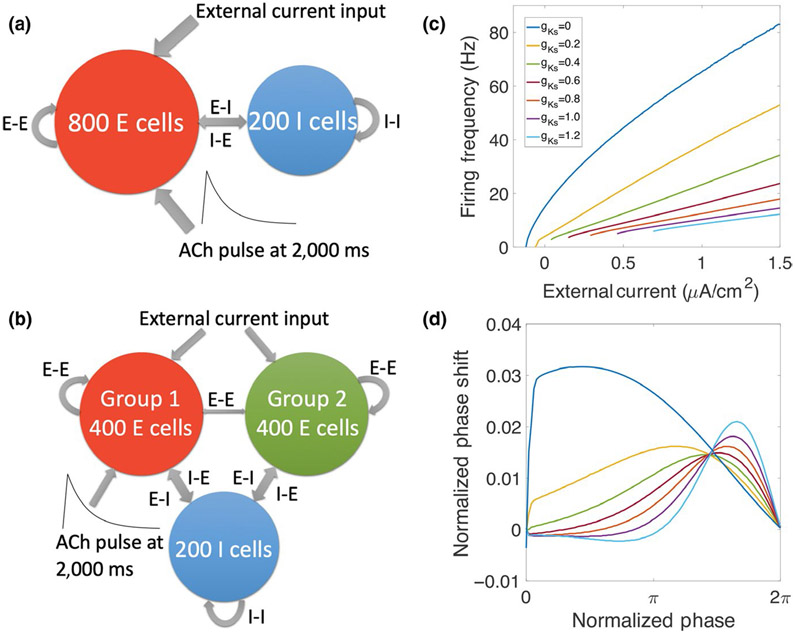
FIGURE 1.

Schematic diagram of network structure and effects of simulated acetylcholine (ACh) modulation on neuronal input–frequency (I–F) curve and phase response curve (PRC). (a) The network consisted of 800 excitatory cells and 200 inhibitory cells with random connectivity within and between groups. Excitatory cells received external noisy input. ACh modulation was simulated by brief down-regulation of the K⁺ M current conductance, g_Ks, applied only to excitatory cells (except in results in Figure 6). (b) In a different network configuration for results in Figure 7, excitatory cells are divided into two groups, where only one group (targeted) receives g_Ks modulation. (c) Current–frequency (I–F) curves for the Hodgkin–Huxley-type model neuron containing the K⁺ M current that is down-regulated by ACh. Different g_Ks values correspond to different ACh levels (see section 2). When g_Ks is low (high ACh), the neurons are more excitable with higher gain and a Type I profile of the I–F curve. Conversely, when g_Ks is high (low ACh), neuron excitability is lower and I-F curves have Type II profiles. (d) Phase response curves (PRCs) for the model neuron at different g_Ks values. When g_Ks is low, brief excitatory applied current pulses induce only advances in time of spike firing (positive phase shifts) regardless of their timing (Type I PRC). At high g_Ks values, brief excitatory stimuli result in either advances or delays (negative phase shifts) of spike firing depending on their timing (Type II PRC)

Heterogeneity in cell dynamics is introduced by varying the external driving current I_app to every excitatory cell (I_app is different for every cell but kept constant throughout the simulation). The amplitude of this external current is chosen to make the intrinsic firing rates of excitatory cells for baseline g_Ks (0.6 mS/cm²) follow a normal distribution with mean frequency of 50 Hz and standard deviation of 5 Hz. Thus, based on the neuronal input–frequency curve (Figure 1c), I_app values were chosen between 2.814 and 3.427 μA/cm². For every inhibitory cell, the baseline current is chosen from a uniform distribution, with mean near current threshold (−0.2 μA/cm²) and standard deviation (0.02 μA/cm²).

2.2 ∣. Network structure

The E–I network consists of 1,000 neurons, among which 800 neurons are excitatory and 200 neurons are inhibitory. The connectivity between every pair of neurons is randomly assigned. Each E cell receives pre-synaptic input from other E cells with probability of 5% (unless otherwise specified) and from inhibitory cells with probability of 30%. Each I cell receives pre-synaptic input from all other cells (both excitatory and inhibitory cells) with probability of 30%. This connectivity is based grossly on that experimentally reported (Ascoli & Atkeson, 2005; Viriyopase, Memmesheimer, & Gielen, 2016).

In the simulations shown in Figure 7, the excitatory cells are divided randomly into two groups with 400 neurons in each group. Other connectivity probabilities are kept the same except that the probability that two excitatory cells from different groups are connected is reduced to 0.5%.

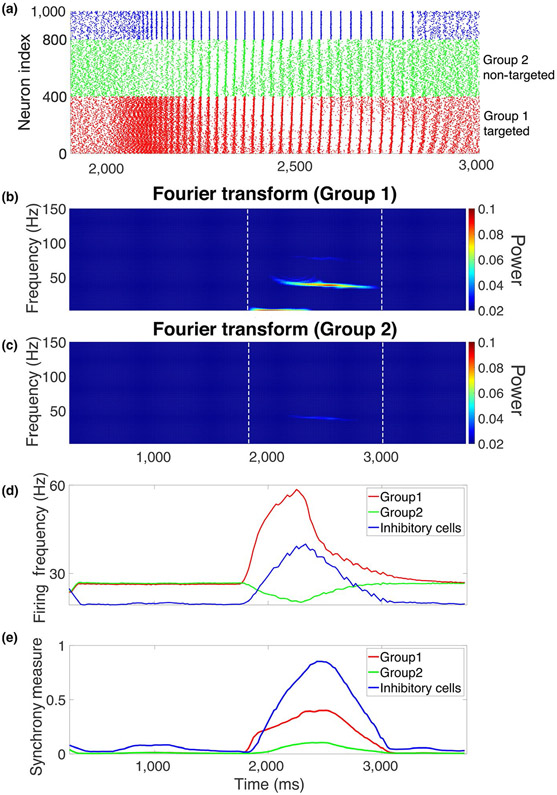
FIGURE 7.

Spatially localized simulated ACh modulation generates local gamma. (a) Raster plot from the network structure illustrated in Figure 1b when the g_Ks transient is only applied to group 1 excitatory cells (red, index: 1–400). During the transient, the activity of group 2 excitatory cells (green, index: 410–800) is slightly inhibited, while the group 1 excitatory cells (red) and inhibitory cells (blue, index: 801–1,000) show higher activity and synchronization. (b, c) Power spectrogram of the simulated local field potential of group 1 excitatory cells and group 2 excitatory cells, respectively. The power of gamma oscillation for group 1 cells is stronger than group 2 cells during the g_Ks transient. Change of average firing frequency over time ([c], see section 2) and change of synchrony measure over time ([d], see section 2) showed that the targeted excitatory cells (group 1, red) and inhibitory cells (blue) increased their firing and synchrony during g_Ks modulation, while non-targeted excitatory cells (green) showed decreased firing and only very weak synchrony during the g_Ks transient

The synaptic current is modeled with a double-exponential profile:

$$I_{\text{syn}}(t)=w_{\text{syn}}\left(V-E_{\text{syn}}\right)\left(\sum _{s_i}{e}^{-(t-s_i)∕{\tau }_{\mathrm{d}}}-e^{-(t-s_i)∕{\tau }_{\mathrm{r}}}\right).$$

In the equation, τ_d is the decay time constant and τ_r is the rise time constant. In the simulations, τ_d = 3 ms for excitatory synapses, τ_d = 5.5 ms for inhibitory synapses, and τ_r = 0.2 ms for all the synapses. The s_i are the firing times of the spikes of pre-synaptic neurons. V is the membrane voltage of post-synaptic neuron and E_syn is the reversal potential of the synaptic current, which is set to be 0 mV for excitatory synapses and −75 mV for inhibitory synapses; w_syn is the maximal conductance of the synaptic current or synaptic strength. The default values are w_ee = 0.004 mS/cm², w_ii = 0.016 mS/cm², w_ei = 0.002 mS/cm² and w_ie = 0.003 mS/cm². In Figure 3 and Figure 6, synaptic conductances were varied as indicated.

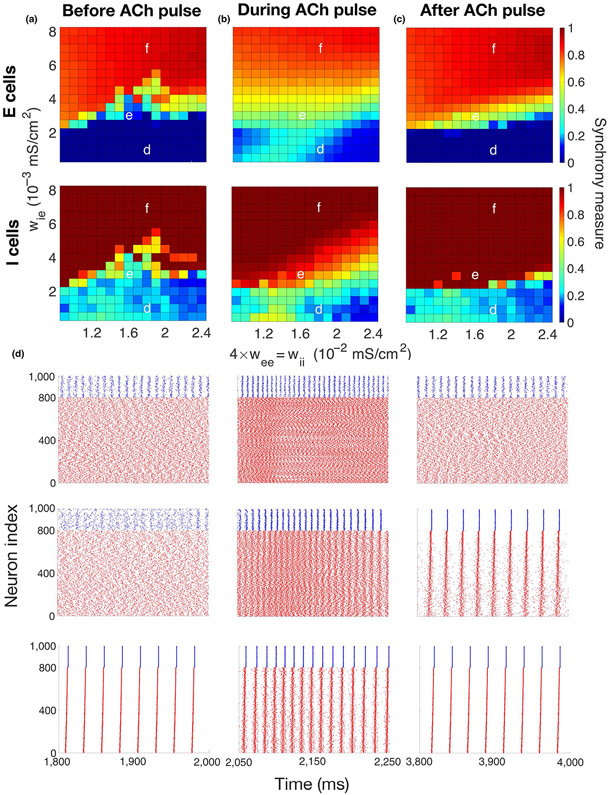
FIGURE 3.

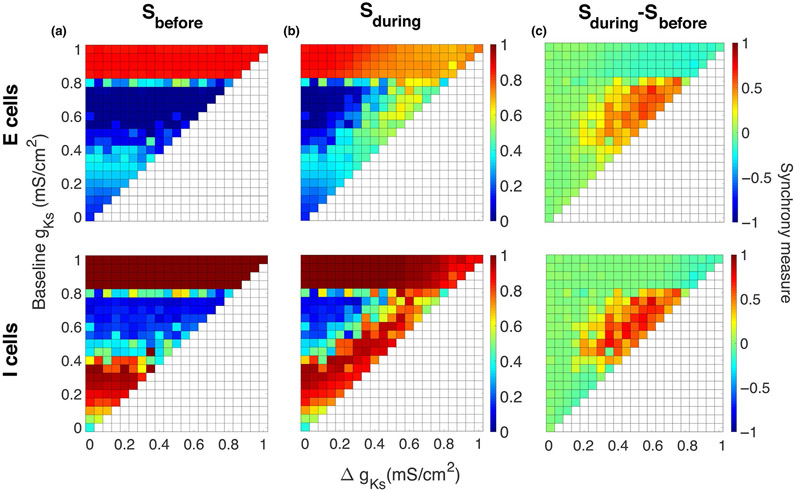
Sensitivity of emergent gamma to network connectivity strength between and among excitatory and inhibitory cells. (a–c) Synchrony measure (color, see section 2) of excitatory cells (top) and inhibitory cells (bottom) computed in 500-ms time intervals before (left panels), during (middle panels) and after (right panels) the simulated ACh transient, averaged over five simulations. Maximum conductances of synaptic currents among the inhibitory cells (I–I synapses, w_ii) and among the excitatory cells (E–E synapses, w_ee = 0.25w_ii) are varied on the x-axis, and maximum conductances of synaptic currents from the inhibitory cells to the excitatory cells (I–E synapses, w_ie) are varied on the y-axis (conductance of E–I synapses was fixed at w_ei = 0.002 mS/cm²). (a) Before the g_Ks transient (1,500–2,000 ms), networks exhibited synchronous or asynchronous firing depending on the connectivity strengths. (b) During the g_Ks transient (2,050–2,550 ms), synchronous gamma oscillations were exhibited by networks in a wider range of connectivity strengths. (c) After the g_Ks transient recovered (3,500–4,000 ms), gamma oscillations were maintained in networks in some synaptic strength parameter regimes (compare with (a)), or network activity returned to the pre-stimulus state. (d–f) Raster plots showing network firing for synaptic strength values indicated in (a–c) during time intervals before (left), during (middle) and after (right) the g_Ks transient (excitatory cells in red and inhibitory cells in blue). The parameter values used in (e) are the same as in Figure 2. External random noise was not included in these simulations

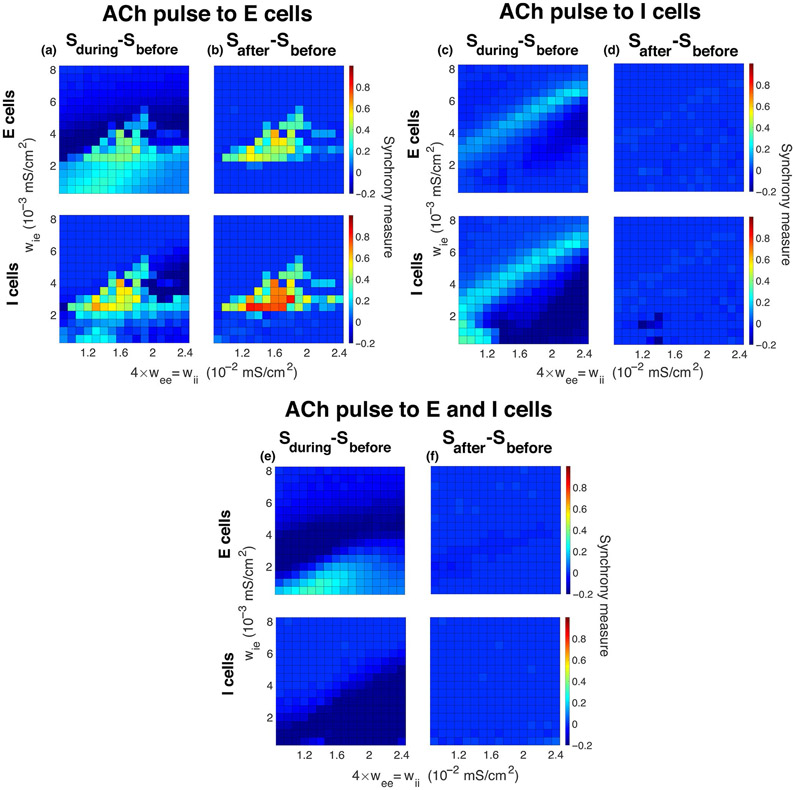
FIGURE 6.

Induction of gamma synchrony by simulated ACh modulation to only inhibitory cells or to both excitatory and inhibitory cells. Differences in synchrony measures (color) between before and during (a, c, e) the g_Ks transient, and between before and after (b, d, f) the g_Ks transient for excitatory cells (top panels) and inhibitory cells (bottom panels) when the transient was applied to only excitatory cells (a, b), to only inhibitory cells (c, d) or to both excitatory and inhibitory cells (e, f). Panel (a) ([b]) is the difference between Figure 3 panels (b) and (a) ([c] and [a]). Simulated ACh modulation to only inhibitory cells or to both excitatory and inhibitory cells did not effectively induce gamma synchrony, and network activity returned to its initial state after the g_Ks transient recovered. External random noise was not included in these simulations

2.3 ∣. Transient ACh pulse

Acetylcholine modulation was modeled as a brief reduction in the maximal conductance of the M current, g_Ks, simulating the post-synaptic effect of ACh mediated by mAChRs. The baseline g_Ks value, $\overline{g_{\text{Ks}}}$, in the excitatory cells and inhibitory cells was set to be 0.6 and 0 mS/cm², respectively (except for simulations in Figure 4 and Figure 6c-f). The g_Ks transient was modeled by $\overline{g_{\text{Ks}}}-\Delta g_{\text{Ks}}(t)$, where −Δg_Ks,(t) is a piecewise function with an initial linear decrease and an exponential recovery (see Figure 2a):

$$\Delta g_{\text{Ks}}(t)=\{\begin{array}{cc}0\hfill & \text{if}t\le t_{\mathrm{p}}\hfill \\ \Delta g_{\text{Ks}}\cdot \frac{t-t_{\mathrm{p}}}{t_{\mathrm{d}}}\hfill & \text{if}{t}_{\mathrm{p}}<t\le t_{\mathrm{p}}+t_{\mathrm{d}}\hfill \\ \Delta g_{Ks}\cdot e^{-\frac{t-t_{\mathrm{p}}-t_{\mathrm{d}}}{c_{\mathrm{r}}}}\hfill & \text{if}t>t_{\mathrm{p}}+t_{\mathrm{d}}\hfill \end{array}\phantom{\}}$$

where t_p is the time that the transient starts and was set to 2,000 ms in all simulations. The decay time t_d was set to 100 ms, so the maximum g_Ks reduction occurred at 2,100 ms. c_r is the recovery constant which reflects the time of g_Ks recovery and was set to c_r = 3,600 ms. With this value, g_Ks recovers to very close to $\overline{g_{\text{Ks}}}$ after approximately 1,500 ms. Δg_Ks represents the amplitude of the g_Ks transient, and its default setting is 0.6 mS/cm² (except in Figure 4). In Figures 2-5 and 7, the g_Ks transient is applied only to excitatory cells. In Figure 4, $\overline{g_{\text{Ks}}}$ and Δg_Ks are varied to study their influence on emergent gamma oscillations. In Figure 6c,d, the default g_Ks transient is applied to only inhibitory cells, and in Figure 6e,f, it is applied to all cells.

FIGURE 4.

Sensitivity of emergent gamma on magnitude of simulated ACh effects. Magnitudes of the maximum conductance of the K⁺ M current before and after the simulated ACh transient, baseline $\overline{g_{\text{Ks}}}$ (y-axes), and of the maximum change in g_Ks during the ACh transient, Δg_Ks (x-axes), were varied. Synchrony measures (color) for excitatory cells (top) and inhibitory cells (bottom) computed in 500-ms time intervals before the ACh transient (a) and during the ACh transient (b). (c) Differences in synchrony measures computed before and during the transient highlight parameter regimes in which gamma synchrony is most affected. Gamma synchrony was reliably induced for moderate values of both baseline $\overline{g_{\text{Ks}}}$ and Δg_Ks (from around 0.4 to 0.8 mS/cm²)

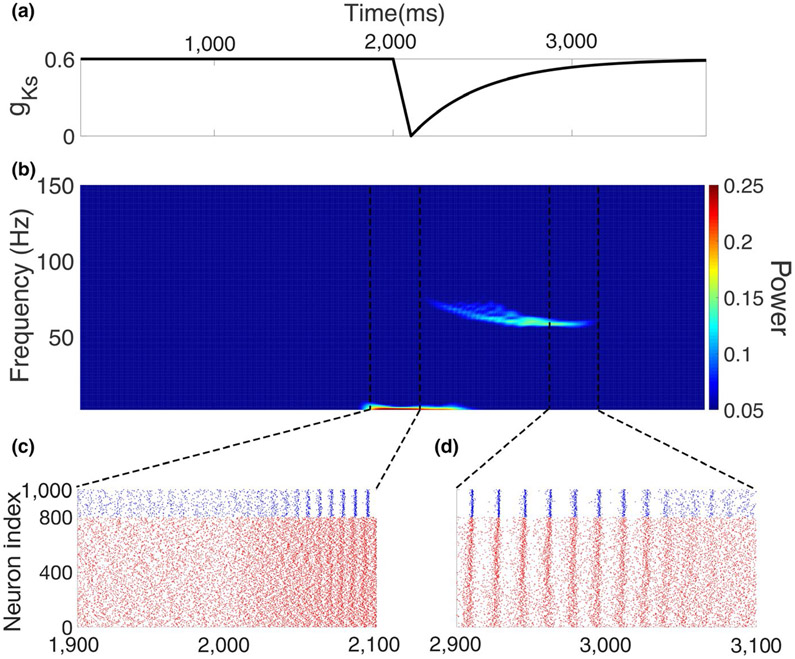
FIGURE 2.

Emergence of gamma oscillations mediated by a simulated ACh transient. (a) Transient change in maximum conductance of K⁺ M current, g_Ks, simulating ACh transient. (b) Power spectrogram computed from simulated local field potential (see section 2). Starting at 2,000 ms, the g_Ks transient led to increasing power in the gamma band. At around 3,000 ms, the gamma power dropped back to the default level with the recovery of g_Ks. (c) Raster plot showing the time range at which the network began to change from asynchronous firing to synchronous gamma oscillations with onset of g_Ks transient (excitatory cells in red and inhibitory cells in blue). (d) Raster plot showing the time range during the recovery of the g_Ks transient when synchronous gamma oscillations gradually dissipated and the network returned to the asynchronized state

FIGURE 5.

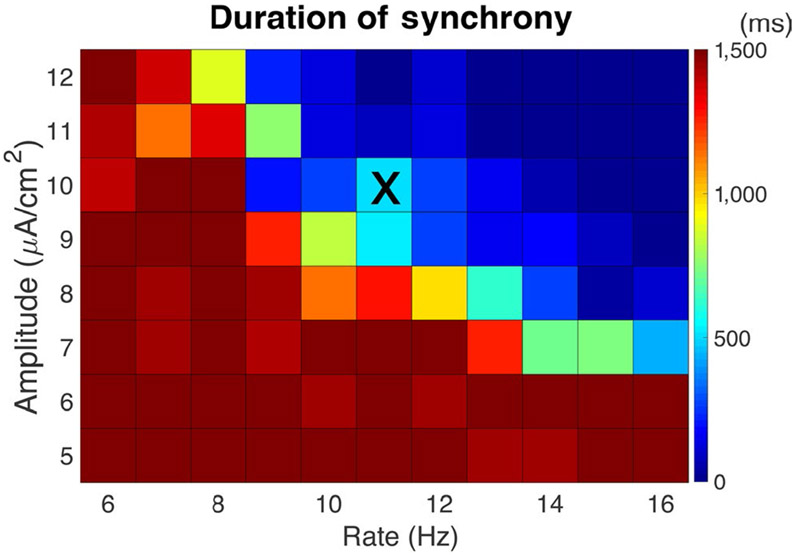
Duration of gamma synchrony in the presence of external random noise. External noise can drive the synchronized network back to asynchrony as the g_Ks transient recovers. Color shows the average time duration (in ms) of gamma synchrony induced by the g_Ks transient for different amplitudes (y-axis) and rates (x-axis) of brief, depolarizing kick stimuli delivered as a random Poisson process to each neuron. When the amplitude and rate were small, synchronous gamma remained stable (duration >1,500 ms) after the g_Ks transient recovered. When the amplitude and/or rate were large, the noise prohibited the network from displaying gamma synchrony even during the g_Ks pulse. Results are averaged over five simulation runs. Noise parameters for simulations displayed in Figure 2 are indicated by “X.”

2.4 ∣. Poisson noise

In Figures 2, 5 and 7, in addition to heterogeneity introduced by different external driving current I_app, random external noisy input in the form of Poisson-distributed, brief, depolarizing “kick” stimuli was applied to both the excitatory cells and inhibitory cells to simulate background noise outside the network from other parts of the brain. In each simulation, the amplitude and Poisson rate of kicks to all cells are fixed at the same values. Each kick was a square applied current pulse of duration 1 ms.

2.5 ∣. Simulation

The codes implementing the simulations were written in MATLAB. All simulations were run for 4,000 ms. Initial conditions for membrane voltages and gating variables were set randomly. Initial conditions for V ranged between −62 and −22 mV; initial conditions for n, h and z ranged between 0.2 and 0.8, 0.2 and 0.8, and 0.15 and 0.25, respectively. The ordinary differential equation system is solved by fourth-order Runge–Kutta method. Results shown in Figures 3-6 were averaged over five simulations.

In sample raster plots in Figures 2, 3 and 7, red represents excitatory cells with indices from 1 to 800 (red and green in Figure 7) and blue represents inhibitory cells with indices from 801 to 1,000. The excitatory cells are sorted so that the cells with the highest driving current I_app are assigned the lowest index, while the cells with lowest driving current are assigned the highest index. The two groups of excitatory cells are sorted separately in Figure 7.

2.6 ∣. Measures

Synchrony measure is used to quantify how well the cells are synchronized in the network by measuring the degree of spike coincidence (Golomb & Rinzel, 1993, 1994). Spike trains for each cell are first convolved with a Gaussian function to form a simulated spike trace, V_i (t). The Gaussian is in the form g (t) = e^{−((t−t₀)2/1.6)} where t₀ is the spike time. The averaged spike trace over all cells V(t) is defined as $V(t)=\frac{1}{N}\sum _{i=1}^N{V}_i(t)$ where N is number of the cells. The variance of individual spike trace σ_i and the variance of the average spike trace σ are defined as

$$\begin{gathered} {\sigma }_i=\langle V_i(t{)}^2\rangle -\langle V_i(t){\rangle }^2 \\ \sigma =\langle V(t{)}^2\rangle -\langle V(t){\rangle }^2 \end{gathered}$$

where <> is the time average over the interval during which synchrony is measured. The synchrony measure is defined as

$$S=\frac{\sigma }{\frac{1}{N}{\sum }_{i=1}^N{\sigma }_i(t)}.$$

Therefore, S = 0 indicates complete asynchrony and S = 1 indicates complete synchrony.

In the figures, synchrony measures are calculated in different intervals relative to the simulated ACh pulse. As the major part of the pulse is contained in the time interval from 2,050 to 2,550 ms, synchrony measure is calculated over this interval to describe network activity during the pulse. Spikes from 1,500 to 2,000 ms and spikes from 3,500 to 4,000 ms are used to calculate the synchrony measure before the pulse and after the pulse, respectively.

To determine duration of synchrony in Figure 5, the synchrony measure of inhibitory cells from 2,000 to 4,000 ms was calculated in 20 time windows of length 100 ms. Time windows with synchrony measure >0.7 were considered synchronized. The threshold of S = 0.7 for inhibitory cells was chosen from observations of raster plots.

The Fourier transform was used to compute the change of power in each frequency band over time. To compute the power spectrogram, simulated spike traces, obtained by convolving spike trains of each cell with the Gaussian function above, were summed across all excitatory cells to simulate a local field potential (LFP). The Fourier transform was applied to the simulated LFP in sliding time windows to obtain the power spectrum over time. The window width was 500 ms with a sliding step size of 10 ms.

In Figure 7, average firing frequency is calculated in a sliding time window to show frequency changes over time. To compute, we define N_k as the number of times that cell k fires in a time window of length T = 500 ms and then compute the average firing frequency in the time window as

$$f=\frac{\sum _{k=1}^j{N}_k}{jT}.$$

The summation is over the groups of ACh-modulated and non-ACh-modulated excitatory cells and inhibitory cells separately where j is the number of cells in each group. Average firing frequency is computed in each 500-ms time window with a 10-ms sliding step size.

3 ∣. RESULTS

3.1 ∣. ACh modulation of neural response properties

Acetylcholine modulates intrinsic membrane excitability of a neuron through muscarinic and nicotinic receptors (m/nAChRs). Guided by neurophysiological evidence, here we concentrated on the effects of ACh modulation through mAChRs and their action on the slow, hyperpolarizing voltage-gated K⁺ M current. We modeled neuronal dynamics using a biophysical cell model based on the Hodgkin–Huxley formalism that incorporates the M current in addition to spike-generating Na⁺ and K⁺ ionic currents. The model, originally developed by Stiefel et al. (2009), is based on experimental recordings of ACh modulation of visual cortex principal cells (Stiefel, Gutkin, & Sejnowski, 2008) (see section 2 for details). We varied the maximal conductance (g_Ks) of the M current in excitatory cells as a proxy for the local ACh level, with g_Ks = 0 mS/cm² corresponding to high ACh level (down-regulation of the M current) and g_Ks = 1.5 mS/cm² corresponding to lowest ACh level (up-regulation of the M current). Here, we specifically investigated the emergence of transient gamma-band rhythmic network activity due to transient increase in ACh level, simulated by transient decrease in g_Ks, mimicking phasic ACh release measured during cued response attentional tasks (Howe et al., 2017).

In this neural model, changes in g_Ks conductance values result in changes to the neuronal input–frequency (I–f) dependence. Namely, with decreasing g_Ks, the neuronal input–frequency (I–f) curve changes from a discontinuous profile (Type II) to a continuous profile (Type I) (Figure 1c) and, at the same time, the neural membrane becomes significantly more excitable, with lower g_Ks significantly elevating the frequency response of the cell to the same level of input. Additionally, decreasing g_Ks induces a simultaneous change in the neuronal phase response curve (PRC; Figure 1d) (Stiefel et al., 2008). The PRC profile changes from Type II for which either delays or advances in spike timing can be induced by a brief excitatory stimulus depending on its timing, to Type I for which spike timing is only advanced by the stimulus. Previous analytical and numerical work has shown that neurons with Type II PRCs are more prone to synchronize compared to cells with Type I PRCs (Bogaard, Parent, Zochowski, & Booth, 2009; Ermentrout, 1996; Fink, Booth, & Zochowski, 2011). We initially focused on g_Ks modulation of excitatory cell responses (g_Ks set to 0 mS/cm² in inhibitory cells), but also considered g_Ks modulation of both cell types.

Model networks were composed of 800 excitatory (E) and 200 inhibitory (I) neurons with random connectivity among and between each cell type (Figure 1a, see section 2 for details). Cells additionally received noisy external synaptic input. First, we investigated effects of global transient g_Ks modulation on the generation of transient gamma rhythmic synchronous dynamics in the network; then, we considered spatially localized, transient g_Ks modulation in a network consisting of two subpopulations of E cells where only one was modulated (Figure 1b), and investigated spatially localized generation of transient gamma oscillatory dynamics.

3.2 ∣. Phasic ACh release promotes emergent gamma oscillations

In our E–I network model, transient decrease in g_Ks changed the network dynamical regime from asynchronous activity to gamma-band oscillations. Interestingly, the emergent gamma could be maintained as a stable state in the network after the phasic g_Ks had recovered, or could be destabilized through external noise, causing the network to revert back to the asynchronous state when the g_Ks transient dissipated. Figure 2 depicts an example of transient emergent gamma in response to phasic g_Ks modulation. Here, the E cells were assumed to contain muscarinic receptors that induce a transient decrease in g_Ks (Figure 2a).

To detect emergence of rhythmic network activity, we computed the Fourier transform of the simulated LFP (see section 2) to show characteristics of network activity in the frequency domain (Figure 2b). Initially, cells fired asynchronously with no rhythmic activity apparent across the network. Keeping all other network parameters the same, as g_Ks decreased, firing rates of all the cells in the network rapidly increased due to changes in E cell-intrinsic excitability (Figure 1c). During the g_Ks decrease, increased power at very low frequencies was observed due to the sharp rise in overall network activity and the simulated LFP. The increased activity from excitatory cells led to the emergence of gamma frequency band synchrony through the so-called PING process (Borgers & Kopell, 2005; Whittington, Traub, Kopell, Ermentrout, & Buhl, 2000; Tiesinga & Sejnowski, 2009). In this process, the increased excitation from E cells leads to increased firing and synchronization of I cells. This, in turn, leads to silencing of the E cells, which when released from inhibition fire synchronously, subsequently driving another synchronous burst of inhibition. Here, gamma-band synchrony emerged as I cell synchrony consolidated during the decrease in g_Ks (Figure 2c) and gamma decayed as g_Ks recovered (Figure 2d). Below, we analyze the reliability of the emergence and maintenance of this gamma-band synchrony as important properties are varied, such as synaptic strengths, the presence of external noise and the efficacy of simulated ACh on the M current. This analysis reveals that inducing gamma rhythms transiently from a background of asynchronous activity depends sensitively on network and modulation characteristics.

3.3 ∣. Sensitivity of emergent gamma to network connectivity

We next investigated to what extent emergence of ACh mediated gamma-band oscillations depended on the properties of network connectivity. To isolate network connectivity effects, the external noisy input to cells was not included. We varied the magnitude of the synaptic conductances from I to E cells (I–E synapses, w_ie, y-axis, Figure 3a-c) and within the excitatory (E–E connectivity, w_ee) and inhibitory (I–I connectivity, w_ii) subnetworks (x-axis, Figure 3a-c) keeping E–I synaptic strength fixed (w_ei fixed at 0.002 mS/cm²). The resultant network dynamics, quantified by the synchrony measure (color in Figure 3a-c, see section 2), within this connectivity parameter space could be divided roughly into three regimes (Figure 3d-f).

With low I–E connectivity, the E–I network did not fully synchronize in response to the g_Ks transient (Figure 3d, bottom region, w_ie < 0.002 mS/cm²). Although excitability of the excitatory cells rose during the g_Ks decrease and therefore inhibitory cells received more input from excitatory cells and became more synchronized, the low I–E synaptic conductance, however, stopped the inhibitory cells from synchronizing the excitatory cells to form PING rhythmicity across the network. Thus, the excitatory cells fire asynchronously before, during and after the g_Ks pulse.

For moderate values of I–E connectivity (w_ie between 0.002 and 0.005 mS/cm²), the network fired asynchronously before the g_Ks transient and synchronized to form gamma oscillations during the transient (Figure 3e). Synaptic strength values for the results shown in Figure 2 are in this regime. Interestingly, for some synaptic strength values within this parameter range, gamma synchrony could be maintained even after the g_Ks transient ended (Figure 3e, right panel), indicating that the network stably generates both asynchronous firing and gamma rhythmicity, and that the g_Ks pulse switches the network between these two regimes. Experimentally, ACh-induced gamma-band synchrony has been observed only transiently, indicating lack of stability of the synchronous gamma regime. We show below that maintained gamma synchrony after dissipation of the g_Ks transient can be easily destabilized by external noisy input to the network.

Finally, for high I–E connectivity (w_ie > 0.005 mS/cm²), the network remains synchronized before, during and after the g_Ks transient, with increased E cell excitability during the pulse acting to increase the frequency of synchronous firing (Figure 3f).

We note that in the low w_ie regime, the I cells were generally more synchronized than the E cells. This I cell synchrony is similar to Interneuron Network Gamma (ING) synchrony as it is generated by the recurrent synaptic coupling among the I cells (Tiesinga & Sejnowski, 2009; Whittington et al., 2000). In some definitions of ING, the I cells should be intrinsically spiking; here, not all I cells spike without input, but the mean external driving current to I cells is close to their current firing threshold and excitation from the E cells promotes their firing. With this characterization of low w_ie regime dynamics, the moderate w_ie regime exhibits bistability between ING and PING dynamics where either state is observed, and the high w_ie regime displays only PING dynamics. In separate simulations, we explicitly tested bistability of ING and PING solutions in the moderate w_ie regime and verified that either solution is maintained depending on the initial conditions of the network state (results not shown).

These results show that inducing transient gamma rhythmicity requires network connectivity characteristics near the regime supporting both ING and PING synchrony. This may restrict properties of the asynchronous network states from which transient ACh can generate gamma oscillations.

3.4 ∣. Sensitivity of emergent gamma to simulated ACh level

We next investigated how the magnitude of simulated effects of ACh on the maximal conductance of the M current, g_Ks, affected the emergence of gamma rhythmicity (Figure 4). To model the g_Ks pulse, g_Ks was set initially to a baseline value, $\overline{g_{\text{Ks}}}$, representing the absence or a low ACh level. During the pulse, g_Ks was dropped to $\overline{g_{\text{Ks}}}-\Delta g_{\text{Ks}}$ as the ACh transient reached its peak. Thus, we can relate Δg_Ks to the peak magnitude of the post-synaptic effects of the ACh pulse. Afterward, g_Ks recovered exponentially back to the baseline level, following the time course depicted in Figure 2a. To measure the efficacy of the g_Ks pulse to induce gamma, we measure network synchrony before the pulse (when $g_{\text{Ks}}=\overline{g_{\text{Ks}}}$, Figure 4a), during the g_Ks transient (Figure 4b), and subsequently calculate the difference (Figure 4c) for E cells (Figure 4, top panels) and I cells (Figure 4, bottom panels) separately.

Results in the parameter space spanned by $\overline{g_{\text{Ks}}}$ (y-axis) and Δg_Ks (x-axis) could be divided into three regimes based on observed dynamics of the network (only values above the diagonal were considered to ensure that the lowest g_Ks value during the pulse, $\overline{g_{\text{Ks}}}-\Delta g_{\text{Ks}}$, was not negative). In the lower left corner, baseline $\overline{g_{\text{Ks}}}$ is low, and Δg_Ks is small amplitude (due to the g_Ks range constraints). Here, even before the g_Ks pulse was applied, the excitatory cells displayed high excitability driving emergence of PING synchrony. During the ACh pulse, the dynamics did not change significantly, resulting in a difference in synchrony near zero (Figure 4c).

In the intermediate baseline regime (for $\overline{g_{\text{Ks}}}$ between 0.4 and 0.8 mS/cm²), the network exhibited asynchronous dynamics before the g_Ks pulse. The left-hand side of this regime corresponds to low magnitude of ACh effects (Δg_Ks small). Here, the increase in excitability of the excitatory cells associated with the g_Ks pulse was not sufficient to drive PING synchrony, and the network remained in an asynchronous firing regime during the g_Ks pulse. However, for larger Δg_Ks, values (center right part of this regime), increased E cell excitability mediated the formation of gamma synchrony during the g_Ks pulse (Figure 4b). This results in a significant increase in synchrony difference (Figure 4c).

In the third regime for high baseline g_Ks $(\overline{g_{\text{Ks}}}>0.8)$, the network exhibited strong synchrony before the g_Ks pulse. This synchrony was, however, not solely mediated by the PING mechanism, as the E cell excitability that drives PING was significantly decreased in this regime. Instead, synchrony was additionally supported by changes in neuronal response properties obtained with high g_Ks values, specifically changes in the PRC. As shown in Figure 1d, for large g_Ks values, the profile of the PRC changes from Type I to Type II facilitating promotion of synchrony. Separate simulations of the network in this regime verify that when synaptic connections from the I cell to the E cells were blocked (w_ie = 0 mS/cm²), synchrony was observed although the synchrony measure was higher with I to E synapses intact due to the PING mechanism (results not shown). Here, in this parameter regime, large Δg_Ks, decreased M current conductance and subsequently shifted the PRC toward a Type I profile resulting in weakened synchrony. Hence, within this regime, the effect of the g_Ks pulse is essentially reversed with less synchrony being observed during the pulse as compared to before its presentation.

Thus, the emergence of transient gamma rhythmicity from a background of asynchronous activity requires sufficient magnitude of the mAChR-mediated post-synaptic effects and tight control of those effects in the absence of ACh.

3.5 ∣. Effects of external noise on duration of emergent gamma

Next, we investigated how external noise affects stability of the emerging synchronous gamma oscillations during the g_Ks transient. This was particularly important as we observed that for noiseless network simulations, gamma oscillations could be maintained after the g_Ks transient subsided. Such a stability in gamma-band oscillations is not observed experimentally. Here, external noise was simulated by brief, depolarizing “kick” stimuli arriving to E and I cells at random times, governed by a Poisson process (see section 2). We measured the duration of synchronous gamma oscillations after the onset of the g_Ks transient as a function of the amplitude and average frequency of the kick stimuli (Figure 5). As expected, stronger and/or more frequent kick stimuli led to shorter duration of synchronous gamma (Figure 5). When both the rate and amplitude of the noisy kicks were small (Figure 5; bottom left corner), synchronous gamma oscillations remained stable indefinitely after the g_Ks transient. On the other hand, when rate and amplitude were both large (Figure 5; top right corner), the network did not achieve a synchronized state even at the minimum of the g_Ks pulse. In the intermediate regime, as the rate and amplitude of kicks increased, the time duration of the synchronous state decreased; moreover, we found that, in this regime, the duration of gamma oscillations rarely exceeded the duration of the g_Ks pulse. In summary, excessive noisy conditions in the network inhibit the emergence of gamma rhythmicity and its duration.

3.6 ∣. Only ACh modulation of excitatory cells promotes strong emergent gamma

In the simulations reported above, simulated ACh effects on the M current occurred only in the E cells. However, it is known that there are inhibitory interneuron types that have muscarinic receptors (Disney & Aoki, 2008). Thus, we investigated whether incorporating ACh modulation of the M current in I cells, instead of E cells, or in both E and I cells could produce synchronous gamma oscillations (Figure 6). The figure displays the differences in network synchrony measured in the E cells (top panels) and in the I cells (bottom panels) between before and during the g_Ks transient (left panels), and between before and after the g_Ks transient (right panels). As the network connectivity regimes where gamma synchrony can occur in these cases may vary, we considered the full ranges of network synaptic strengths where E cell g_Ks modulation had the strongest effects (as in Figure 3; for example, Figure 6a displays the difference of Figure 3b and Figure 3a). We observed that g_Ks modulation of the E cells had the most pronounced effects for the transition to gamma-band synchrony (Figure 6a,b), whereas g_Ks modulation to only the I cells (Figure 6c,d) or to both E and I cells (Figure 6e,f) induced only slight changes in network synchrony.

When only I cells were modulated (Figure 6c,d), the g_Ks transient caused increases in synchrony only for network connectivity parameters in the regime where E cells showed synchronous firing prior to the g_Ks transient (see Figure 3a). However, for high w_ii values (lower right corner), synchrony of I cells dropped during the g_Ks pulse, due to increased excitability leading to increased inhibition among them. With almost all connectivity parameters, network dynamics returned to their initial state after the g_Ks pulse even without the presence of external noise.

When g_Ks modulation was applied to both E and I cells simultaneously (Figure 6e,f), we observed increases in gamma-band synchrony only with the combination of small I–E connectivity and relatively small intra-connectivity. But again networks returned to their initial state after the g_Ks transient.

Hence, emergence of gamma rhythmicity depended strongly on mAChR-mediated effects primarily occurring in excitatory cells. Simulated ACh modulation of only the I cells resulted in increases in gamma synchrony in parameter regimes exhibiting synchrony before the modulation, similar to previously reported effects of attentional modulation of I cells (Buia & Tiesinga, 2006).

3.7 ∣. Spatially localized ACh modulation induces spatially localized gamma

Finally, as recent experimental results indicate that cholinergic signaling is spatially focused rather than broadly distributed across networks (Sarter & Lustig, 2020), we investigated effects of spatially localized g_Ks modulation on generation of spatially localized gamma oscillations. Here, E cells are divided into two groups (Figure 1b)—only the targeted group (red) received g_Ks modulation; in the non-targeted group (green), g_Ks remained at its baseline level throughout the simulation (Figure 7). As the transient was applied to the targeted excitatory group, its firing rate, as observed earlier, significantly increased (Figure 7a,d). This increased excitatory drive increased I cell firing and eventually caused them to synchronize. All E cells, including the non-targeted group, received inhibitory signaling. As a consequence, firing frequency in the non-targeted group decreased (Figure 7a,d). As I cell synchrony consolidated, PING-mediated gamma-band oscillations emerged in both E cell groups (Figure 7b,c,e); however, power in the gamma frequency band was significantly stronger in the targeted group than in the non-targeted group. Gamma oscillations were weak in the non-targeted group due to their lower excitability that caused longer recovery times from the synchronous inhibitory input. The increased excitability of the E cells in the targeted group allowed them to recover faster and generate another burst of excitation to drive the next inhibitory burst before the non-targeted E cells could fully recover. Hence, the targeted group displayed both significant enhancement of firing frequency and power of gamma-band synchrony over the non-targeted group. This spatial localization of gamma-band oscillations possibly provides for enhanced firing pattern readout from localized ensembles of cells within a network.

4 ∣. DISCUSSION

Motivated by recent evidence for fast, phasic and spatially localized ACh signaling in cortical networks and its generation of transient gamma rhythmicity, we investigated its underlying neuronal network-based mechanisms using biophysical computational modeling of E–I networks. Post-synaptic ACh effects were simulated by the blockade of the muscarinic M-type K⁺ conductance g_Ks in excitatory cells based on experimental evidence showing the reliance on muscarinic receptors for the generation of gamma rhythmicity (Howe et al., 2017). Our results show that simulated ACh transients, causing increases in E cell excitability, induced gamma-band rhythmic firing through a PING mechanism, as might be inferred from previous findings (Borgers et al., 2005) (Buia & Tiesinga, 2006, 2008; Tiesinga & Buia, 2009; Tiesinga et al., 2001). However, we show that the reliability of the generation of gamma rhythmicity from a background of asynchronous activity depends sensitively on important network and modulation characteristics. In particular, the emergence of gamma oscillations depended on synaptic connection strengths among E cells and among I cells, while connection strengths from I to E cells had a larger role in causing synchronous gamma oscillations in the absence of simulated ACh. The presence of external noise in the network affected the generation and duration of gamma oscillations. Interestingly, for some network connectivity regimes in the absence of external noise, induced gamma oscillations were sustained even after the simulated ACh transient completely dissipated. This suggests that networks can support bistable states involving PING dynamics and, conversely, that external mechanisms might be needed to eliminate gamma oscillation after ACh diminishes. Including simulated ACh modulation of the I cells, in addition to or instead of the E cells, was not as effective in generating gamma oscillations, although it affected synchrony as previously shown (Buia & Tiesinga, 2006). Lastly, we showed that spatially localized simulated ACh modulation induced gamma oscillations in a subset of cells in a network without recruiting the entire network in the rhythmic activity, which may contribute to the selective processing of stimuli (see below).

In the behavioral cue detection experimental results, the observed ACh-induced gamma-band activity occurred over a range of frequencies (Howe et al., 2017). Specifically, in response to the cue, there was an initial burst of high-frequency gamma synchrony (75–90 Hz) followed by longer-lasting lower gamma frequency activity (47–57 Hz). Our simulation results show a similar variation of gamma frequency in response to the g_Ks pulse, namely frequencies decrease over the range of approximately 90–50 Hz during the pulse (see Figure 2b). This frequency decrease follows the time course of the g_Ks transient; however, the frequency values are determined by the PING mechanism. While the experimentally observed high- and low-frequency gamma activity may be associated with different mechanisms (Howe et al., 2017), our results suggest that a variation in gamma frequency can be the result of variation in the efficacy of ACh modulation.

In this study, we focused on the modulation of cortical circuitry mediated by muscarinic cholinergic receptors (mAChRs). In the motivating experimental study, Howe et al. (2017) concluded that activation of mAChRs was the basis for the long-lasting gamma rhythms induced by cue-associated ACh transients. Cholinergic effects mediated by nicotinic receptors (nAChRs), on the other hand, modulated only initial transient gamma activity observed at cue onset. As additional justification, based on effects of nAChR activation in neocortical circuits (Colangelo, Shichkova, Keller, Markram, & Ramaswamy, 2019), their effects may also act to contribute to generation of gamma oscillations by the mechanisms described here. Specifically, activation of nAChRs pre-synaptically modulates cortical pyramidal cell synaptic transmission leading to increases in glutamatergic synaptic signaling. Some studies report that inhibitory interneurons are the post-synaptic targets of the boosted signaling (Couey et al., 2007; Obermayer et al., 2018; Urban-Ciecko, Jouhanneau, Myal, Poulet, & Barth, 2018). These effects align with the PING mechanism for gamma oscillations that relies on strong excitatory drive to inhibitory cells and with previous modeling studies showing promotion of ING and PING synchrony with increased excitatory drive to inhibitory cells (Buia & Tiesinga, 2006). Activation of nAChRs has also been reported to increase excitability of neocortical pyramidal cells (Hedrick & Waters, 2015). While this excitability increase may be mediated by changes in intracellular Ca²⁺ activity, rather than by modulation of membrane K⁺ currents as occurs with mAChR activation, it would likewise promote gamma rhythmicity by a PING mechanism.

A number of other computational modeling studies have investigated the role of ACh in attention and processing of sensory inputs (Borgers et al., 2005; Borgers & Kopell, 2008; Deco & Thiele, 2011; Hasselmo et al., 1992; Kanamaru, Fujii, & Aihara, 2013; Tiesinga et al., 2001) (see (Newman et al., 2012) for review). In particular, these studies address how ACh modulates network dynamics to support selectivity in network responses to competing external stimuli, or winner-take-all dynamics, as would occur in selective attention tasks (Thiele & Bellgrove, 2018). The contribution of gamma oscillations in selective attention was included in Borgers and Kopell (2005) and Borgers and Kopell (2008) where, in the presence of competing external excitatory stimuli, ACh modulation promoted increased gamma activity in the subset of cells receiving stronger stimuli. These studies consider diverse effects of ACh modulation on neuron and network properties including modulation of mAChR-mediated K⁺ currents (Borgers & Kopell, 2005) and additional K⁺ and Ca²⁺ currents (Tiesinga et al., 2001), increases in inhibitory synaptic activity (Borgers & Kopell, 2008), decreases in inhibitory synaptic activity (Kanamaru et al., 2013), or some combination of these effects (Deco & Thiele, 2011; Hasselmo et al., 1992). In related modeling studies of selective attention in visual cortical circuits, attention, simulated as changes in top-down or sensory-associated excitatory drive to E and/or I cells, facilitated selective responses and increased gamma-band oscillations and synchrony (Buia & Tiesinga, 2008; Tiesinga & Buia, 2009).

Our results point to a slightly different mechanism for selectivity in processing of competing external stimuli. Namely, spatially localized ACh could bias the network response to be dominated by the activity of the affected excitatory neurons. Their interaction with local inhibitory neurons can induce spatially localized gamma which provides the network oscillatory dynamics necessary to promote cognitive processing of stimuli introduced in that local area of the network. Multiple lines of evidence support the contributions of gamma oscillations as important for cognition (Buzsaki & Wang, 2012; Cannon et al., 2014) and integration of sensory input (Singer & Gray, 1995). Thus, we hypothesize that spatially localized ACh-induced gamma primes the network for successful cognitive processing of spatially coincident stimuli. This provides an additional mechanism or dynamical layer for priming an attentionally activated subnetwork toward integration of sensory information via gamma-band oscillations and biasing the network response to be driven by that subpopulation.

Abbreviations:

ACh

acetylcholine

BF

basal forebrain

E

excitatory

g_Ks

maximal conductance of M-type K⁺ membrane ionic current

I

inhibitory

I–f

input–frequency

ING

Interneuron Network Gamma

LFP

local field potential

mAChR

muscarinic M1 acetylcholine receptor

nAChR

nicotinic acetylcholine receptor

PING

Pyramidal-Interneuronal Network Gamma

PRC

Phase response curve

DATA AVAILABILITY STATEMENT

All computer codes implementing model results will be posted on a publicly accessible site upon publication of the manuscript.