An intra-host SARS-CoV-2 dynamics model to assess testing and quarantine strategies for incoming travelers, contact management, and de-isolation

Summary

Non-pharmaceutical interventions (NPIs) remain decisive tools to contain SARS-CoV-2. Strategies that combine NPIs with testing may improve efficacy and shorten quarantine durations. We developed a stochastic within-host model of SARS-CoV-2 that captures temporal changes in test sensitivities, incubation periods, and infectious periods. We used the model to simulate relative transmission risk for (1) isolation of symptomatic individuals, (2) contact person management, and (3) quarantine of incoming travelers. We estimated that testing travelers at entry reduces transmission risks to 21.3% ([20.7, 23.9], by PCR) and 27.9% ([27.1, 31.1], by rapid diagnostic test [RDT]), compared with unrestricted entry. We calculated that 4 (PCR) or 5 (RDT) days of pre-test quarantine are non-inferior to 10 days of quarantine for incoming travelers and that 8 (PCR) or 10 (RDT) days of pre-test quarantine are non-inferior to 14 days of post-exposure quarantine. De-isolation of infected individuals 13 days after symptom onset may reduce the transmission risk to <0.2% (<0.01, 6.0).

Highlights

• •A novel, stochastic model of intra-host SARS-CoV-2 viral dynamics
• •Captures clinical dynamics of symptom onset, infectiousness, and detectability
• •Designed to evaluate residual transmission risks after arbitrary NPI strategies
• •Implemented in a freely available software (van der Toorn et al., 2021)

The bigger picture

In 2020, the COVID-19 outbreak turned into a pandemic. Non-pharmaceutical interventions (NPIs) remain decisive tools to prevent SARS-CoV-2 transmission and contain the spread of novel viral variants. Strategies that combine NPIs with SARS-CoV-2 testing may help to improve efficacy and shorten the duration of quarantine, thereby reducing the socioeconomic burden of SARS-CoV-2.

We derived a novel intra-host viral dynamics model that realistically represents time-dependent infectiousness and test sensitivity profiles. We utilized this model to quantify the transmission risk reduction of combined NPI and testing strategies in different contexts. The underlying model is designed for rapid evaluation and flexibility in formulating NPI strategies and has been compiled into a user-friendly software (van der Toorn et al., 2021) that allows users to design and evaluate arbitrary NPIs schemes with regard to their efficacy in reducing the risk of SARS-CoV-2 onward transmission.

We developed an intra-host SARS-CoV-2 dynamics model that realistically captures time-dependent infectiousness and test sensitivity profiles. The model is used to quantify transmission risk reduction of combined non-pharmaceutical intervention (NPI) and testing strategies in different contexts. The underlying model is designed for rapid evaluation and flexibility in formulating NPI strategies and has been compiled into a user-friendly software (see van der Toorn et al., 2021).

Introduction

The SARS-CoV-2 outbreak began with a cluster of pneumonia cases of unknown origin in Wuhan City, China.¹ In January 2020, Chinese authorities imposed a cordon sanitaire on Wuhan, but corona disease 2019 (COVID-19) cases had already been exported to countries outside of China;² the World Health Organization (WHO) declared a pandemic in March 2020.³ Since then, SARS-CoV-2 has continued to spread globally. At the time of writing, over 100 million cases of COVID-19 have been confirmed worldwide, including over 2 million deaths.⁴ Given the high fatality rate of COVID-19,5, 6, 7 emerging evidence of its mid- or even long-term sequelae,8, 9, 10, 11, 12, 13, 14 as well as its capacity to overwhelm health care systems15, 16, 17, 18 and inflict economic damage,^19,20 it is imperative to contain—or at least mitigate—the spread of SARS-CoV-2.

Although scientific progress has been made at unprecedented speed, resulting in rapid expansion and improvement of therapeutic modalities,21, 22, 23, 24, 25, 26, 27, 28 curative treatment options are still lacking; vaccines of high efficacy have been developed and approved,^29,30 but (1) they may not be available in sufficient amounts to achieve population-level impact at the global scale in the near future³¹ and (2) some vaccines may not protect against new variants of concern.31, 32, 33, 34, 35 Non-pharmaceutical interventions (NPIs) are currently, and will remain, important measures to curb SARS-CoV-2 spread for as long as the pandemic is ongoing. The large-scale lockdowns implemented by governments all over the world during the first and second waves of the pandemic have proven extremely successful at controlling the outbreak and limiting the number of deaths, but induced significant economic damage.^36,37 As lockdowns were gradually lifted, many of the more limited NPIs were maintained, with the goal of keeping the number of infections low and maintaining an effective reproduction number at time t (Rt) of <1. These NPIs include social distancing and hygiene measures, mask mandates, and restrictions on public gatherings. In addition, given that a substantial fraction of SARS-CoV-2 transmissions originate from asymptomatic and pre-symptomatic individuals,38, 39, 40, 41, 42 a combination of public health measures termed test-trace-isolate (TTI) is key to all successful containment strategies. TTI involves: (1) diagnostic testing that prioritizes, but is not limited to, symptomatic cases; (2) isolation of confirmed cases; and (3) tracing and quarantining exposed contacts.⁴³ TTI is usually complemented with quarantine for incoming travelers. The term “isolation,” which refers to the separation of people with confirmed infection, is distinct from the term “quarantine,” which refers to the separation of people who were—potentially or certainly—exposed to SARS-CoV-2. For quarantine, the WHO recommends a length of 14 days,⁴⁴ and for isolation, a length of at least 13 days.⁴⁵ However, it is not rare for different strategies to be implemented at the national and sub-national or institutional levels. This may be due to perceived socioeconomic pressures;⁴⁶ to staffing concerns, especially with respect to health care workers when hospital systems are under strain;⁴⁷ or to patient care considerations, given the detrimental effect that long isolation periods can have, for example, on cognitively impaired patients.⁴⁸ In these settings, testing is frequently used to shorten the duration of quarantine and/or isolation. Given that antigen-based rapid diagnostic tests (RDTs) are being used increasingly,⁴⁹ strategies that are based on combined testing and quarantine/isolation criteria may gain even more momentum in the near future.

Through mathematical modeling, strategies have been proposed that combine regular surveillance testing and isolation of test-positive cases to enable regular service in, e.g., educational institutions.^50,51 This seminal work has been complemented by real-world data, where such approaches have been successfully implemented in businesses, in some professional sports disciplines,⁵² as well as in health care and nursing facilities.⁵³ Recently, Slovakia performed massive nation-wide diagnostic screens for SARS-CoV-2, which were followed by a notable prevalence decrease.^54,55 Such large-scale approaches have previously not been implemented for the general public, due to cost and logistic constraints. Also, the suitability of employing voluntary mass testing to end the epidemic has been controversial.⁵⁶

The durations of quarantine and isolation are under ongoing scrutiny to find an ideal balance between infection prevention and the socioeconomic consequences they impose and have been the focus of several modeling studies.^43,57, 58, 59, 60, 61 Herein, we developed a model of within-host infection dynamics that enable assessing arbitrary quarantine-testing and isolation strategies with respect to their capacity for reducing SARS-CoV-2 transmission risk.

Currently, WHO recommendations for quarantine are based on the maximum incubation time observed in studies done during the beginning of the pandemic,^44,62 whereas national guidelines on quarantine and testing may sometimes be determined in the political discourse. While consultation with researchers helps to improve strategies, quantifying the added benefit of a strategy adaptation is often impossible, at least in a timely manner. We aim to fill this gap by (1) consolidating our current knowledge on SARS-CoV-2 infection dynamics and (2) computing the consequential reduction in transmission risk for differential quarantine, isolation, and testing strategies. In addition, (3) the applicability domain of the model covers different risk-posing scenarios (contact management, travelers, and isolation). The model has been developed into a user-friendly software⁶³ that offers total flexibility in the design of NPIs, allows corroborating a policy-making discourse with realistic numbers while the discussion is ongoing, and can be easily updated to reflect new clinical results.

Results

The viral dynamics model reproduces known incubation-, infectivity-, and time-dependent test sensitivity profiles

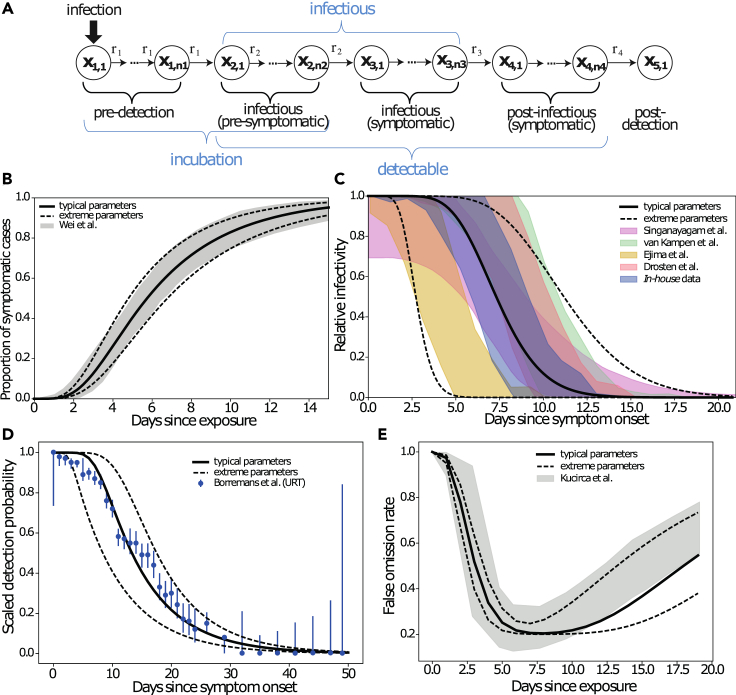
The stochastic transit compartment model utilized is shown in Figure 1A. The model consists of five phases (incubation, pre-symptomatic, symptomatic, post-symptomatic, and post-detection). Each phase is sub-divided into several sub-compartments, which allows one to capture inter-individual differences as well as the shape of SARS-CoV-2 infection dynamics (Figure S1; Table 1. We have carefully calibrated the model’s default parameters to reproduce published and in-house clinical data on the incubation time,⁶⁴ the offset of infectiousness after peak virus load/symptom onset (T.C. Jones, personal communication),65, 66, 67 and the time-dependent test sensitivities (Table 2).^68,69

Figure 1.

Model validation

Published and data-derived SARS-CoV-2 intra-patient dynamics (shaded areas), as well as model-predicted dynamics with default parameters (lines).

(A) Model structure.

(B) Duration of incubation. The cumulative time-to-symptom onset from a meta-analysis of 56 studies is shown (gray-shaded areas),⁶⁴ together with the model-predicted time-to-symptom onset (solid line, typical dynamics; dashed lines, upper and lower extremes).

(C) Relative infectiousness after symptom onset/peak viral load extracted from Singanayagam et al. and van Kampen et al.,^65,66 deduced from in-house data (supplemental experimental procedures) and derived from viral load kinetics reported by Ejima et al.,⁶⁷ are shown as shaded areas, whereas model-predicted infectiousness profiles are depicted by lines (solid line, typical dynamics; dashed lines, lower and upper extremes).

(D) Time-dependent PCR sensitivity after symptom onset reported by Borremans et al.⁶⁹ (error bars) together with model-simulated PCR sensitivity using default parameters (solid line, typical dynamics; dashed lines, lower and upper extremes).

(E) Time-dependent false omission rate as reported by Kucirca et al.⁶⁸ (shaded area). Solid and dashed lines show model simulations with typical and upper/lower extreme parameters. Details on the parameter fitting procedure and analysis of infectivity profiles are provided in the experimental procedures and supplemental experimental procedures.

Table 1.

States of the underlying Markov model

j	State	Detectable	Infectious	Symptoms
1	pre-detection	no	no	no
2	pre-symptomatic	yes	yes	no
3	infectious (and symptomatic)	yes	yes	(yes)+
4	post-infectious (and symptomatic)	yes	no	(yes)+
5	post-detectable	no	no	no

⁺Asymptomatically infected individuals are assumed to have the same infection dynamics without symptoms.

Table 2.

Model parameters

	Pre-detection		Pre-symptomatic		Infectious		Post-infectious
	$n_1$	${\tau }_1$	$n_2$	${\tau }_2$	$n_3$	${\tau }_3$	$n_4$	${\tau }_4$
Step 1	estim.	estim.	fix∗	estim.
Step 2					estim.	estim.
Step 3	✓	✓	✓	✓	✓	✓	fix∗	estim.
Final parameter estimate	5	2.86 (2.38; 3.37)	1	3.91 (3.27; 4.62)	13	7.5 (2.79; 11.47)	1	8

The three steps in the estimation procedure to derive parameters from available clinical data are highlighted. Estimated parameters for the respective step are indicated as “estim.” and fixed parameters are denoted as “fix.” Parameters that are carried forward from the preceding estimation step are highlighted by checkmarks (✓). Asterisk (∗) indicates fixed to 1. The last row depicts the derived default parameters, with extreme values in parentheses.

Figure 1B shows the cumulative time to symptom onset (gray-shaded area) compiled in a meta-analysis of 56 studies,⁶⁴ together with the model predictions (solid and dashed lines) using the default parameters. As can be seen, the utilized model reproduces not only the mean duration of incubation but also the entire waiting time distribution. Figure 1C shows a summary of datasets used to evaluate the duration of infectiousness after peak virus load/symptom onset (shaded areas) (T.C. Jones, personal communication),65, 66, 67 including the analysis of in-house data (experimental procedures and supplemental experimental procedures). The depicted data are scaled to represent the relative reduction in infectiousness assessed by culture positivity, as well as viral load dynamics (details on the data analysis and parameter fitting procedure are provided in the experimental procedures). While Singanayagam et al. and van Kampen et al.^65,66 report relative culture positivity over time, we used the in-house data to derive and fit a mechanistic model (supplemental experimental procedures) that allows converting virus load profiles post-symptom onset into infectivity profiles. We used the mechanistic model to derive infectivity profiles from viral loads reported by Ejima et al.⁶⁷ and Charité (T.C. Jones, personal communication).

The infectiousness profiles show a marked dispersion between different studies, which may be partly due to the investigation of different cohorts (mild-moderately ill⁶⁵ versus hospitalized severely ill patients⁶⁶), differences in the definition of “symptom onset,” and methodological differences in the laboratory assays used to assess infectiousness. We adjusted the model’s default parameters to each study individually and derived parameter ranges that capture the entire range of infectivity profiles. Figure 1D shows the decrease in detection probability,⁶⁹ whereas Figure 1E shows the reported time-dependent false omission rate ${\text{FOR}}_t\left(\mathbf{x}\right)$ of the PCR diagnostics (shaded areas),⁶⁸ as well as respective model-predicted dynamics with default parameters (lines). As shown, the model captures the time-dependent assay sensitivity reasonably well with default parameters. A small deviation at the beginning (broad range of reported uncertainty in the data) may be due to uncertainties in determining the time of symptom onset (Figure 1D) and infection (Figure 1E).

In summary, the developed model, with default parameters, integrates the current state of knowledge on SARS-CoV-2 infection dynamics into a single mathematical model that can be used for designing non-pharmaceutical SARS-CoV-2 control strategies.

The viral dynamics model allows quantification of the concurrent effects of quarantine and testing strategies

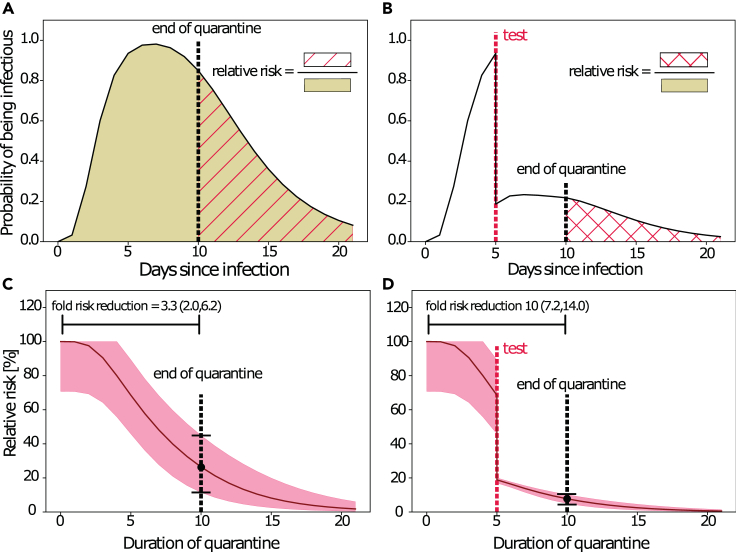
For illustration, we simulate a time course of infectiousness for a virtual patient cohort held in quarantine after exposure (Figure 2A). In this illustrative example, an individual is released from quarantine at day 10. This allows quantification of the relative risk emanating from this individual in terms of the ratio of the area under the infectivity curve from the end of quarantine (hatched area) versus the entire interval (shaded area). In Figure 2B, a diagnostic test is performed at day 8. If the test is positive, the individual will go into isolation, and consequently not pose a risk. Therefore, the probability that the individual is actually infectious and not in quarantine is decreased in relation to the false omission rate at the time of the diagnostic test. Again, the relative risk is the ratio of the area under the infectiousness curve from the end of the quarantine (crosshatched area in Figure 2B), relative to the entire interval (shaded area in Figure 2A). The time profiles of the corresponding percentage relative risks for the two illustrative scenarios are shown in Figures 2C and 2D. The corresponding fold risk reduction (=1/relative risk(t)) for 10 days quarantine would be 2.6 (1.90; 5.26) and would be 10.0 (7.2; 14.0) for a 10 day quarantine with a PCR test on day 5, as indicated by the horizontal bars in Figures 2C and 2D. In the testing and quarantine example (Figures 2B and 2D), the pre- and post-test quarantine had a minor effect on the risk reduction, whereas the test reduced the relative risk considerably. In this example, the pre-test quarantine increased the test sensitivity considerably, making the combined strategy effective. In summary, these examples illustrate how the model can be used to assess the concurrent effects of quarantine and testing strategies.

Figure 2.

Simulation of quarantine and testing strategies

(A) Model-simulated probability of infectiousness. The shaded area indicates the transmission risk emanating from an infected individual. If a quarantine were imposed until day 10 (dashed black vertical line), the risk of transmission would relate to the red-hatched area. Hence, the relative risk denotes the risk after the quarantine divided by the risk without quarantine.

(B) Model-simulated probability of infectiousness when a test (dashed red vertical line) was performed at day 5. If the test were positive, the person would go into isolation, thus not posing a risk, whereas there would be a residual risk that the person was infectious if the test were negative (false negative). The risk after a 10 day quarantine (dashed black vertical line) with a test at day 5 is indicated by the red-crosshatched area.

(C) Relative risk profile for a pure quarantine (as exemplarily shown in [A]). Line, typical parameters; shaded area, extreme parameters.

(D) Relative risk profile for a testing and quarantine scenario (as exemplarily shown in [A]). Line, typical parameters; shaded area, extreme parameters.

Next, we use the model to assess NPI strategies. Therein, we focus on three scenarios in particular: (1) isolation of symptomatic individuals, (2) management of individuals with a known time of exposure (contact management), and (3) quarantine of incoming travelers. The three scenarios can easily be simulated by adjusting the initial conditions $p_{t_0}\left(\mathbf{x}\right)$ of the model.

Calculations for quarantine and testing strategies in contact management

Strategies for contact management focus on reducing the risk emanating from individuals who have been in contact with a confirmed case. In this scenario, we assume that the time of the last exposure, $t_0$, is known and equals the time of the putative infection. Hence, all entries in $p_{t_0}\left(\mathbf{x}\right)$ are set to zero, except for $x_{\mathrm{1,1}}$.

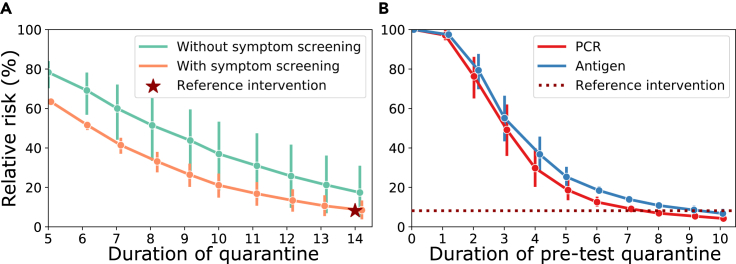
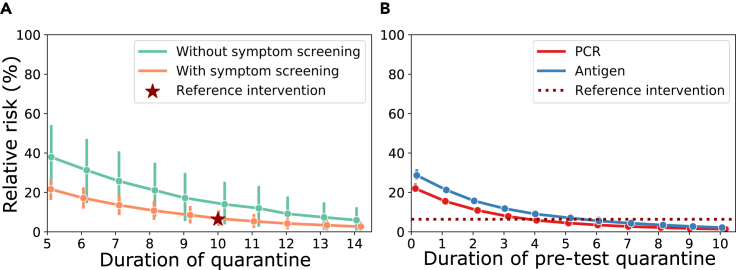
Using the model with default parameters, we calculated the percentage relative risk during quarantine with and without “symptom screening” (Figure 3A). Symptom screening was implemented as follows: if individuals develop symptoms, they stay isolated and hence do not pose a risk (compare Equation 12). Note that in these simulations we considered 20% of cases to be asymptomatic, and thus never developing symptoms. As can be seen, symptom screening markedly reduces the relative risk. For example, after 14 days of quarantine, the relative risks are 8.18% (4.5, 12.7) versus 16.31% (5.6, 30.3) for contact person management with and without symptom screening, respectively. Currently, the WHO and several national guidelines recommend 14 days of quarantine in combination with symptom screening for contact management.⁴⁴ We will use the model-derived estimate (relative risk of 8.18%) to suggest a combined testing and quarantine strategy that has an equivalent efficacy. We will focus on testing strategies in which a test is conducted after a pre-test quarantine. In the case of a negative test result, the person is immediately released from quarantine; in the case of a positive test result the person stays isolated and does not pose a risk. For the antigen test, we assumed a relative sensitivity of 85% compared with PCR, as outlined in the experimental procedures.

Figure 3.

Risk reduction through quarantine and testing strategies in contact management

(A) Calculated percentage relative risk during quarantine with and without symptom screening relative to no intervention. The WHO recommendation (14 day quarantine with symptom screening) is marked as the reference intervention (red star). Line, typical parameters; error bars, extreme parameters.

(B) Calculated percentage relative risk for combined test and quarantine strategies. Here, an individual goes into a pre-test quarantine with a diagnostic test at the end of it, which, when negative, results in the release from quarantine. The reference efficacy (14 day quarantine with symptom screening) is indicated by a horizontal dotted red line. All calculations were performed with parameters from Table 2 and assuming 20% asymptomatic infections, solving Equations 9 and 13. We assumed that exposure occurred on day 0 (today), with $p_{t_0}\left(x_{j,i}\right)=1$ for $\left(j,i\right)=\left(\mathrm{1,1}\right)$ and $0$ for all other $(j,i)$. Line, typical parameters; error bars, extreme parameters.

Figure 3B shows relative risks for combined quarantine and testing strategies using default simulation parameters and assuming symptom screening. Our assessments show that testing before day 5 in contact person management has limited effects on risk reduction. Furthermore, a PCR test at day 8 versus an antigen test at day 10 would result in a non-inferior relative risk (<8.18%) compared with the WHO guidelines.⁴⁴ Importantly, in addition to allowing one to shorten quarantine duration, a benefit of testing is that it allows one to detect asymptomatic cases. Moreover, it reduces the uncertainty in the risk reduction assessment: for example, a quarantine of 14 days in contact person management with symptom screening reduces the risk to stay within the bounds 4.5%–12.7% (mean ~8.18%). The equivalent combined quarantine and testing strategy of 8 days (PCR), with respect to 10 days (antigen test), tightens the confidence bounds to 6.33%–7.47% (PCR) and 5.02%–8.41% (antigen test), effectively reducing the uncertainty by a factor 7.2 (PCR) and ~2.4 (antigen test).

The viral dynamics model can be used for prevalence estimation

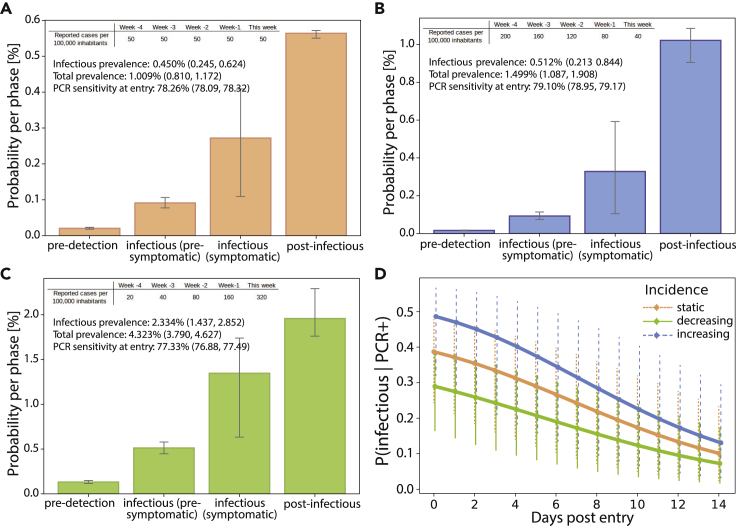
Based on a recent incidence history, the model can be used to compute the anticipated SARS-CoV-2 prevalence in the setting of interest, as outlined in the experimental procedures. Moreover, it also computes which phase of infection individuals from the defined setting are expected to be in, which can have consequences for quarantine and testing strategies. In Figures 4A–4C, we show the model-predicted prevalence of infected and infectious individuals, as well as the probability of PCR positivity, depending on whether the incidence is stable (Figure 4A), on the rise (Figure 4B), or declining (Figure 4C; the incidence parameters used are stated in the caption). Corresponding model-predicted probabilities of detecting infectious individuals among the PCR-positive specimens in the days post-entry are depicted in Figure 4D, showing differing utility to filter out potential spreaders in the settings considered.

Figure 4.

Pre-entry risk calculation for incoming travelers

(A–C) (A) Prevalence estimation for travelers entering from a country with 20% probability of detection ($P\left(\text{detect}\right)=20\%$) and a stable incidence (50 cases/100,000/week for the last 5 weeks), (B) a declining incidence (200, 160, 120, 80, 40 cases/100,000/week for the last 5 weeks), and (C) a rising incidence (20, 40, 80, 160, 320 cases/100,000/week for the last 5 weeks). Typical dynamics; error bars and values in parentheses, upper and lower extremes.

(D) Time-dependent probability of detecting infectious individuals among the PCR-positive specimens in the respective cohorts of travelers in the days post-entry. Calculations were performed as outlined under “prevalence estimator” in the experimental procedures. Typical dynamics; error bars and values in parentheses, upper and lower extremes.

In summary, if the provided incidence history resembles the force of infection in a region of travel, the model can be used to inform differential quarantine and testing strategies for returning travelers coming from high-risk areas with active or waning pandemic dynamics. Next, to evaluate strategies for incoming travelers, we first use the proposed prevalence estimation method to obtain the probability distribution at the time of travel, $p_{t_{\text{entry}}}\left(\mathbf{x}\right)$, based on a given incidence history. We then set $p_{t_0}\left(\mathbf{x}\right)=p_{t_{\text{entry}}}\left(\mathbf{x}\right)$ and assess quarantine and testing strategies for incoming travelers.

Calculations for quarantine and testing strategies for incoming travelers

Using the model with default parameters, we calculated the percentage relative transmission risk during quarantine for incoming travelers (stable incidence history) (Figure 5A).

Figure 5.

Risk reduction through quarantine and testing strategies for incoming travelers (stable incidence of 50 cases/100,000 inhabitants/week; $P\left(\text{detect}\right)=20\%$)

(A) Percentage relative risk during quarantine with and without symptom screening (20% asymptomatic, default parameters). A 10 day quarantine with symptom screening is marked as the reference intervention (red star), according to current German guidelines. Typical dynamics; error bars, upper and lower extremes.

(B) Percentage relative risk for combined testing and quarantine strategies. In the simulated scenario, individuals go into a pre-test quarantine with a diagnostic test at the end of it, which, when negative, results in the release from quarantine. The reference efficacy (10 day quarantine with symptom screening) is indicated by a horizontal dotted red line. All calculations were performed with parameters from Table 2 and assuming 20% asymptomatic infections, solving Equations 9 and 13. Typical dynamics; error bars, upper and lower extremes.

Because some travelers could have been exposed prior to entering, a proportion may already have progressed through their infection. Therefore, greater risk reductions can be achieved for incoming travelers compared with contact management of recently exposed individuals. For example, after 14 days of quarantine, the relative risks are 2.32% (1.06, 4.57) versus 4.69% (1.31, 11.79) for incoming travelers with and without symptom screening, respectively. In comparison, for contact management, the relative risks were 8.18% (4.51, 12.7) versus 16.31% (5.57, 30.30).

The current German guidelines recommend 10 days of post-entry quarantine with symptom screening for incoming travelers, which amounts to a relative risk of 6.39% (3.64, 10.24). Figure 5B shows risk reductions for combined quarantine and testing strategies using default simulation parameters and assuming symptom screening. As before, PCR or antigen testing is conducted at the end of the quarantine to release individuals if they have a negative test result. Under the parameters used, a single PCR test at day 4 post-entry (6 days for antigen) reduced the risk for incoming travelers (unknown time of infection) in a similar manner compared with a 10 day quarantine after entry (Figure 5B).

Notably, these simulations assume that incoming travelers are exposed to the infection dynamics provided by the incidence history (here, stable incidence) and that there is no elevated risk for the actual travel. For travelers that become infected during their travels, the contact management calculations hold.

Calculations for isolation and testing strategies for symptomatic individuals (de-isolation)

The model can also be used to assess the management of symptomatic individuals. Strategies for symptomatic individuals focus on the duration of the isolation period. In this scenario, we assume symptom onset (peak viral load) to be at $t_0$. Hence, all entries in $p_{t_0}\left(\mathbf{x}\right)$ are set to zero, except for $x_{\mathrm{3,1}}$.

The calculated percentage relative risk with default parameters for different isolation durations are shown in Table 3. The fraction of infectious individuals decreases substantially (compare also Figure 1B). Under the parameters used, the relative transmission risk after 10 days of isolation post-symptom onset is 2.10% (<1 × 10⁻¹⁰, 18.15), and after 13 days it is 0.17% (<1 × 10⁻¹⁰, 6.01). However, it should be mentioned that the uncertainty in these estimates is large, as depicted in the parentheses.

Table 3.

Calculated percentage relative risk for isolation and time-dependent informative value of the PCR based on default parameters, with extreme values in parentheses

Duration of isolation (days)	Percentage relative risk	$P_t\left(PC{R}^{+}\right)$	PPV	NPV
5	34.25 (0.11, 56.50)	0.79 (0.61, 0.80)	0.91 (0.01, 0.99)	0.13 (<0.01, 0.99)
6	23.20 (0.00072, 47.85)	0.78 (0.54, 0.80)	0.77 (<0.01, 0.98)	0.32 (0.03, 1.00)
7	14.41 (0.00037, 39.37)	0.75 (0.48, 0.80)	0.60 (<0.01, 0.95)	0.55 (0.08, 1.00)
8	8.22 (1.7 × 10−5, 31.55)	0.70 (0.42, 0.79)	0.42 (<0.01, 0.89)	0.75 (0.18, 1.00)
9	4.32 (<1 × 10−10, 24.33)	0.65 (0.37, 0.77)	0.27 (<0.01, 0.80)	0.87 (0.32, 1.00)
10	2.10 (<1 × 10−10, 18.15)	0.59 (0.33, 0.75)	0.16 (<0.01, 0.70)	0.94 (0.48, 1.00)
11	0.96 (<1 × 10−10, 13.02)	0.53 (0.29, 0.72)	0.09 (<0.01, 0.59)	0.98 (0.63, 1.00)
12	0.41 (<1 × 10−10, 9.00)	0.47 (0.25, 0.67)	0.05 (<0.01, 0.47)	0.99 (0.76, 1.00)
13	0.17 (<1 × 10−10, 6.01)	0.42 (0.22, 0.63)	0.02(<0.01, 0.37)	0.99 (0.84, 1.00)
14	0.06 (<1 × 10−10, 3.88)	0.37 (0.20, 0.58)	0.01 (<0.01, 0.28)	0.99 (0.91, 1.00)

We assumed symptom onset at day 0, with $p_{t_0}\left(x_{j,i}\right)=1$ for $\left(j,i\right)=\left(\mathrm{3,1}\right)$ and $0$for all other $\left(j,i\right).$ We report the probability of a positive PCR, $P_t\left({\text{PCR}}^{+}\right)$, as well as its positive and negative predictive value (PPV, NPV) with regard to detecting infectious individuals at the end of the isolation period.

Diagnostic testing for de-isolation is less straightforward compared with testing during quarantine and requires a differentiated approach. The probability of having a positive PCR and the positive predictive value (PPV) of the PCR with regard to detecting infectious individuals are shown in columns 3 and 4 of Table 3: the PPV is high initially (>0.9 after 5 days of isolation) and drops rapidly from there. Therefore, a positive PCR result alone is not an appropriate criterion for retaining in isolation a person who has already completed an isolation period by symptom- or duration-based clinical criteria. Also, the prediction range, due to inter-individual differences in viral kinetics, is very wide. The negative predictive value (NPV) of the PCR with regard to assessing non-infectiousness is initially very low (<0.3 before day 6) and increases to >0.9 after 10 days of quarantine (see column 4 in Table 3). This implies that negative testing of isolated individuals is informative only after a considerable duration of isolation. Hence, testing individuals at these time points may ascertain their non-infectiousness, but it may not be a reasonable tool to shorten the isolation period in general, because the test becomes informative only after ~10 days of isolation. In summary, this analysis indicates that combining PCR testing and isolation has limited benefit compared with isolation alone. Exceptions may arise when individuals shed virus for much longer than typical.

Discussion

As of April 2021, the COVID-19 epidemic is ongoing and many Northern Hemisphere countries are experiencing a third severe wave of cases. Although many countries have initiated a vaccination program and some have already vaccinated a large proportion of their population, it is not yet clear when vaccines will be widely available globally or what their long-term clinical efficacy will be. Thus, non-pharmaceutical control strategies, including testing, isolation, and quarantine will remain an integral part of SARS-CoV-2 control for a considerable time.

To help optimize these strategies, we have developed a within-host viral dynamics model that allows the evaluation and deduction of non-pharmaceutical SARS-CoV-2 mitigation strategies based on quarantine, testing, and isolation.

The underlying mathematical models and methods of the proposed model are entirely novel.

What sets this work apart from most other efforts to date is its detailed mapping of the in-host viral dynamics^43,57, 58, 59 to the population-level spread, which allows a rich and realistic representation of time-dependent sensitivities and specificities of different testing procedures (e.g., PCR and antigen tests) and thereby of the effectiveness of using such tests for different isolation and quarantine strategies. The model thus synthesizes the current state of knowledge on within-host infection dynamics and utilizes it to enable the rational, evidence-based design of non-pharmaceutical control strategies. Another main advantage is that we compile this model into a software, as described in van der Toorn et al.⁶³ The software allows the user to design and evaluate self-designed NPIs, rather than to rely on pre-computed scenarios that may not enable decision-makers to evaluate the precise NPI of interest.

The software can be accessed via https://github.com/CovidStrategyCalculator/CovidStrategyCalculator.

Given that the model reproduces the statistical attributes of population dynamics, we see the prime field of application in providing rational, evidence-based guidance to policy makers determining test, quarantine, and isolation strategies at the national and sub-national levels. Individual infection dynamics may differ from the ensemble dynamics, depending, for example, on age, known or unknown pre-existing conditions, disease severity, and other factors that may affect the duration of viral shedding.70, 71, 72 Thus, while the model is suitable for determining a strategy that has maximum benefit for most cases in a population, this approach may not be optimal for each individual case. In other words, the model may not be well suited to select an individual- or case-specific NPI regimen, especially in the context of, e.g., pre-existing conditions or critical disease. The model’s default parameters capture typical mean incubation periods (5.6–8.0 days) that correspond to mean/median incubation times reported in the literature (Backer et al., 6.4 days; Linton et al., 5.6 days; Lauer et al., 5.1 days; Li et al., 5.2 days^62,73, 74, 75). However, outliers have been reported, for example, in immunodeficient individuals or the elderly.^76,77 Likewise, the mean duration of infectiousness post-symptom onset with the model’s default parameters lies within the range of 2.8–11.5 days, which is well supported by current knowledge (compare Figure 1C) (Singanayagam et al., median 4 days; van Kampen et al., median 8 days; Arons et al., 6–9 days; Wölfel et al., <8 days; COVID-19 Investigation Team, <9 days).^65,66,78, 79, 80 We have assumed, for our model, that infectiousness decreases sharply due to both viral decay and virus neutralization. Of note, patients with severe or critical illness may shed infectious virus considerably longer⁸¹ (van Kampen et al., up to 20 days; Jeong et al., up to 15 days; Xiao et al., 18 days),^66,72,82 as may immunocompromised individuals (Koff et al., 20 days; Choi et al., 143 days).^70,76 Therefore, in the setting of severe disease or immunocompromise, de-isolation may be approached differently, for example, conditioned on a negative PCR test. In addition to these patient-specific differences, a number of other factors can contribute to apparent heterogeneities observed in the analyzed studies (Figure 1C). Among those may be differences in the definition of symptom onset, differences in sampling (samples from either upper or lower respiratory tract), the time lapse between sample deduction and culture experiment, and intrinsic variabilities in virus deduction from swabs (discussed further below), as well as differences in the analyzed cohort. For example, van Kampen et al.⁶⁶ describe the duration of infectiousness in hospitalized elderly patients (severe cases, median age 65, 20% immunocompromised), whereas Singanayagam et al.⁶⁵ analyze mildly symptomatic cases (average age ~52).

Our model captures the time-dependent sensitivity of diagnostic assays. For PCR, we modeled the “clinical sensitivity,” which takes into account (1) analytical sensitivity (which depends on technical performance parameters and is extremely high) and (2) common pre-analytical issues (e.g., inadequate specimen collection), which may lead to insufficient quantities of virus genetic material and ultimately false negative results.⁸³ While the quantities of genetic material obtained through swabbing may correlate with individual viral loads, they are confounded by “random effects” associated with the specimen collection process (type of swab used and accessibility of sampling site). Our modeling demonstrates that these random effects or “noise” are considerable (Fig. SN2 in the supplemental experimental procedures) and may limit our ability to detect differences between, e.g., age or risk groups.

For antigen-based RDTs, we assumed that sensitivity kinetics resemble those of PCR, albeit with lower analytical sensitivity.^49,84,85 This approach was chosen because clinical data on the kinetics of RDT sensitivity are currently limited.⁸⁶ For anterior-nasal antigen tests, the sensitivity parameters of the model can be adjusted. Typically, sensitivity would be measured with regard to the gold standard (“PCR”), as implemented in the software (tab “Parameters”). Current estimates are 74% relative sensitivity,⁸⁷ but this may depend on the specific RDT used.⁸⁸ Moreover, sensitivities may be different in different groups, especially in pre- and asymptomatic individuals. The available model implementation⁶³ can be refined with regard to test-sensitivity dynamics as soon as robust data are available.

The presented model allows us to compute the infection prevalence based on the recent COVID-19 incidence history in the setting of interest (compare Figure 4) and to incorporate this knowledge into the rational design of testing strategies. For prevalence estimation, the model is simulated using the incidence values for the preceding 5 weeks at initial values. Moreover, one can define the percentage of SARS-CoV-2 cases that have actually been diagnosed. The “percentage diagnosed” has been the focus of intense research with highly conflicting predictions.89, 90, 91, 92, 93, 94 To date, there is no reliable estimate of this parameter, which is likely influenced by changes in testing strategies and variations in testing capacities over time. In a related, entirely genomics-driven approach, we are quantifying the temporal change in this parameter; the resulting data will be used in conjunction with the model presented here.

In addition to the already presented calculation examples in Figures 3 and 5 and Table 3, the following general statements can be made for NPI strategies:

• •Testing, when conducted at time points with high diagnostic sensitivity, can substantially reduce the duration of quarantine while offering equivalent risk reduction. This corroborates finding by Wells et al.⁵⁹ and is due to the fact that testing facilitates the identification of infected individuals, regardless of whether they develop symptoms or not. Not all such asymptomatic or pre-symptomatic individuals may be removed from the infectious pool by quarantine alone. Of note, to ensure equivalent risk reduction, the use of less sensitive tests entails a smaller reduction in quarantine duration. This may have important implications with respect to antigen-based RDTs. We observed that testing can reduce the uncertainty in the percentage relative transmission risk; this is an additional benefit of a combined testing and quarantine strategy.
• •Diagnostic testing for reducing the duration of isolation requires a differentiated approach: A negative test can be informative regarding the non-infectiousness of an individual (high NPV) only after a minimum isolation time has passed (approximately 10 days). In contrast, a positive test does not necessarily imply infectiousness. However, testing viral replication as a surrogate for infectiousness, as suggested by Huang et al.,⁹⁵ or integrating information about the viral loads might facilitate a combined testing and de-isolation approach in the future. Also, RDTs could be more suitable than PCR for de-isolating individuals.
• •Releasing pre-symptomatic, infected individuals from quarantine bears a much larger risk of onward transmission, because these individuals can potentially infect others over a longer time period compared with de-isolated individuals, whose infectiousness is already decreasing. On the other hand, only a fraction of individuals in quarantine are actually infected, whereas a majority of isolated individuals are infectious.

Scope, limitations, and future advancements

The focus of the presented work is to estimate the efficacy of NPIs at the level of the individual, i.e., the presented model allows quantification of the efficacy of different NPIs in reducing the risk emanating from a potentially infected individual. Often, epidemiological models focus on the population impact by considering the spreading process on compartmental models (e.g., SEIR [susceptible, exposed, infectious, recovered]) or more realistic agent-based approaches.^92,96, 97, 98 The efficacy terms derived herein (e.g., relative risk) can easily be incorporated as scaling parameters in such epidemiological models to estimate, e.g., country- or city-specific NPI efficacies. Along these lines it is then also possible to project the effects of NPIs on Rt or the concomitant effects of both NPIs and vaccination on the pandemic, or to use the presented model in contexts where the effectiveness of contact tracing^99,100 with subsequent NPIs is modeled.

As a future perspective, the model could also be used to explore travel behavior, i.e., inferring the time of infection with regard to travel, when only the times of positive PCR and symptom onset in returning travelers are available.

Experimental procedures

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Max von Kleist (kleistm@rki.de).

Materials availability

This study did not generate new materials.

Data and code availability

All datasets used during this study were previously published, with the exception of the in-house data, which are available from the lead contact on request. The software is available at https://github.com/CovidStrategyCalculator/COVIDStrategyCalculator.

Model of infection dynamics

We modeled the time course of SARS-CoV-2 infection using a stochastic transit compartment model based on the Markov jump process formalisms (discrete state, continuous time), as depicted in Figure 1A. Herein, an individual is modeled as a random variable whose state changes through time. The nodes $x_j$ of the model reflect the states of infection that an individual will progress through after a random waiting time. This formalism can be used to sample thousands of individual infection trajectories and compute the ensemble statistics thereof (e.g., proportion of individuals who are infectious at a given time instance), akin to Duwal et al.^101,102 Below, we will derive a set of ordinary differential equations that compute these probabilities straight away without the need for sampling, allowing one to model inter-individual differences in, e.g., time to detectability or time to infectiousness.

We distinguish five different states by whether (1) the virus is detectable, (2) the individual has symptoms, and (3) the individual may be infectious (Table 1). These three attributes describe a minimal set of properties important to evaluate SARS-CoV-2 non-pharmaceutical control and testing strategies, allowing one to select time points for testing, incorporate symptom-based screening, and quantify the residual risk at the end of a testing or quarantine strategy. Notably, asymptomatic infections are also included in our simulations. For asymptomatic individuals, we assume the same infection dynamics without displaying symptoms.

To control the shape of the infection time course, we introduce the notion of a “phase.” In our model, a phase $j$ is defined as a set of $n_j$ subsequent nodes $x_{j,i}$. The transition rates $r_j$ between the nodes $x_{j,i}$ in phase $j$ are trivially related to the average duration that an infected individual stays in a phase, the mean residence time ${\tau }_j$:

$$r_j=\frac{n_j}{{\tau }_j}\text{.}$$ (Equation 1)

However, the shape of this residence time changes with the number of compartments. Given the mean residence time of a phase, we can change the skewness of the transitioning times by adjusting the number of compartments in that phase until the model reflects the statistical attributes of the SARS-CoV-2 time course of infection sufficiently well. An example is shown in Figure S1, where the addition of nodes to the phase introduces a “shoulder” without affecting the mean duration of the phase. Because the model is descriptive, the sub-compartments of a phase have no clear physical interpretation.

The equations that model the probability that individuals are in phase $j=1\dots 5$ at time $t$ is given by:

$$\begin{array}{l}\frac{d}{dt}{p}_t\left(x_{\mathrm{1,1}}\right)=-r_1\cdot p_t\left(x_{\mathrm{1,1}}\right)\text{,}\\ \dots =\dots \end{array}$$ (Equation 2)

$$\frac{d}{d_t}{p}_t\left(x_{1,n_1}\right)=r_1\cdot p_t\left(x_{1,n_1-1}\right)-r_1\cdot p_t\left(x_{1,n_1}\right)\text{,}$$ (Equation 3)

$$\begin{array}{l}\frac{d}{d_t}{p}_t\left(x_{\mathrm{2,1}}\right)=r_1\cdot p_t\left(x_{1,n_1}\right)-r_2\cdot p_t\left(x_{\mathrm{2,1}}\right)\text{,}\\ \dots =\dots \end{array}$$ (Equation 4)

$$\frac{d}{d_t}{p}_t\left(x_{5,n_5}\right)=r_4\cdot p_t\left(x_{4,n_4}\right)\text{.}$$ (Equation 5)

Here, $p_t\left(x_j\right)=\sum _{i=1}^{n_j}{p}_t\left(x_{j,i}\right)$ and the last phase $j=5$, the “post-detection phase,” is a one-node absorbing state. In matrix notation, the model is given by $\frac{d}{d_t}{p}_t\left(\text{x}\right)=A\cdot p_t\left(\text{x}\right)$, with:

$$A=\left(\begin{array}{llllllll}-r_1\hfill & 0\hfill & \cdots \hfill & \hfill & \hfill & \hfill & \cdots \hfill & 0\hfill \\ r_1\hfill & -r_1\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & ⋮\hfill \\ 0\hfill & r_1\hfill & -r_1\hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ ⋮\hfill & \hfill & \ddots \hfill & \ddots \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & r_1\hfill & -r_2\hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \ddots \hfill & \ddots \hfill & \hfill & \hfill \\ ⋮\hfill & \hfill & \hfill & \hfill & \hfill & r_4\hfill & -r_4\hfill & ⋮\hfill \\ 0\hfill & \cdots \hfill & \hfill & \hfill & \cdots \hfill & 0\hfill & r_4\hfill & 0\hfill \end{array}\right)\text{.}$$ (Equation 6)

Therefore, the system can be solved analytically with:

$$p_t\left(\mathbf{x}\right)=e^{t\cdot A}\cdot p_{t_0}\left(\mathbf{x}\right)\text{,}$$ (Equation 7)

where $e^{t\cdot A}$ denotes the matrix exponential and $p_0\left(\text{x}\right)$ denotes the initial condition of the system.

This model structure allows sufficient flexibility to resemble clinically observed infection dynamics and enables the direct use of published quantities in model simulations, such as the “mean duration of the incubation phase.”

Calculation of relative risk and risk reduction

The goal of NPIs, such as quarantine or isolation, is to reduce the risk of onward transmission. The risk of onward transmission is related to the probability that the individual is—or may become—infectious and to the duration of this infectious period. In our model, we assume that the area under the curve of the time-dependent probability of being infectious, $\underset{t}{\overset{\infty }{\int }}{P}_s\left(\text{inf}\right)ds,$ is proportional to the risk of onward transmission. To calculate the integral, we augment the matrix $A$, such that:

$$\tilde{A}=\left(\frac{A}{0\mathbf{y}0}|\frac{\mathbf{0}}{0}\right)\text{,}$$ (Equation 8)

with $y_j=1$ in the last row of the matrix for all “infectious states,” $j=2,3$. When solving for $p_{\infty }\left(\tilde{\mathbf{x}}\right)=e^{s\cdot \tilde{A}}\cdot \left(\begin{array}{l}{p}_t\left(\mathbf{x}\right)\hfill \\ 0\hfill \end{array}\right);s\to \infty$, using standard numerical schemes (e.g., the Higham scaling and squaring algorithm),¹⁰³ the risk $\underset{t}{\overset{\infty }{\int }}{P}_s\left(\text{inf}\right)ds$ is given by the last entry of the derived vector, i.e., $p_{\infty }\left({\tilde{x}}_{N+1}\right)$.

We use this method to calculate the residual risk: the risk that an individual who is released from an NPI is able to spread the disease. We define ${p_t}_{\text{end}}\left(\mathbf{x}\right|\text{NPI})$ as the probability state vector conditioned on the implementation of an NPI that ended at time $t_{\text{end}}$. To assess the efficacy of an NPI we calculate the relative risk¹⁰⁴ with regard to the baseline risk (the setting without any NPI or other restrictions):

$$relativerisk\left(t_{\text{end}}\right)=\frac{{\int }_{t_{\text{end}}}^{\infty }{P}_s\left(\text{inf}\right|\text{NPI})d}{{\int }_0^{\infty }{P}_s\left(\text{inf}\right|\varnothing )ds}\text{,}$$ (Equation 9)

where $\underset{t_{\text{end}}}{\overset{\infty }{\int }}{P}_s\left(\text{inf}|\text{NPI}\right)ds$ integrates over the conditional probability of being infectious after release from quarantine at time $t_{\text{end}}$, whereas $\underset{0}{\overset{\infty }{\int }}{P}_s\left(\text{inf}|\varnothing \right)ds$ integrates over the probability of being infectious in the case where the person had not been isolated or put into quarantine (baseline risk). Herein, we assume no additional (e.g., behavioral) differences between the two settings. As both the denominator and the nominator in Equation 9 use the same initial condition, $p_{t_0}\left(\mathbf{x}\right)$, the initial prevalence factors out (compare Equation 13 below). This allows us to compare the efficacy of NPI strategies in a prevalence-independent manner. In the discussion, we explain how the relative risk may be computed with regard to different baselines. Conversely, the fold risk reduction is calculated as:

$$foldriskreduction\left(t_{\text{end}}\right)=\frac{1}{relativerisk\left(t_{\text{end}}\right)}\text{.}$$ (Equation 10)

To account for incomplete adherence to the NPI with fraction $w$, the relative risk can be computed as $relativerisk\left(t_{\text{end}}\right)=\frac{w\cdot {\int }_{t_{\text{end}}}^{\infty }{P}_s\left(\text{inf}|\text{NPI}\right)ds+\left(1-w\right)\cdot {\int }_0^{\infty }{P}_s\left(\text{inf}|\varnothing \right)ds}{{\int }_0^{\infty }{P}_s\left(\text{inf}|\varnothing \right)ds}$.

Modeling non-pharmaceutical interventions

Formally, we define three mutually exclusive situations for an individual to be in: non-contained, quarantined, or isolated. Of these, only non-contained individuals pose the risk of onward transmission.

Quarantine is a measure that applies to symptom-free individuals without a confirmed infection, whereas isolation applies to individuals with symptoms or a confirmed infection. We further define two key strategic tools to use in combination with quarantine or isolation: symptomatic screening and testing. In the case of symptomatic screening, individuals who develop symptoms are assumed to go into isolation. For testing, we assume that a positive test implies that the tested individual stays in, or goes into, isolation. These assumptions correspond to those used in current WHO guidelines.^44,45,49 The case of non-adherence to these basic guidelines is covered as described above.

Symptomatic screening acts upon the transition from the second phase (pre-symptomatic) to the third phase (symptomatic): instead of transitioning to the third phase, the individuals who develop symptoms go into isolation. Asymptomatic individuals, however, do transition and continue to pose a risk. To model symptomatic screening, we update $A$ (and by extension$\tilde{A}$) to depend on $f_s$ (=fraction of symptomatic cases) and the Boolean variable SCR (whether or not symptomatic screening is performed):

$$A(\text{SCR},f_s)=\left(\begin{array}{llllllll}-r_1\hfill & 0\hfill & \cdots \hfill & \hfill & \hfill & \hfill & \cdots \hfill & 0\hfill \\ r_1\hfill & -r_1\hfill & \hfill & \hfill & \hfill & \hfill & \hfill & ⋮\hfill \\ 0\hfill & r_1\hfill & -r_1\hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ ⋮\hfill & \hfill & \ddots \hfill & \ddots \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \left(1-f_s\cdot \text{SCR}\right)\cdot r_2\hfill & -r_3\hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \ddots \hfill & \ddots \hfill & \hfill & \hfill \\ ⋮\hfill & \hfill & \hfill & \hfill & \hfill & r_4\hfill & -r_4\hfill & ⋮\hfill \\ 0\hfill & \cdots \hfill & \hfill & \hfill & \cdots \hfill & 0\hfill & r_4\hfill & 0\hfill \end{array}\right)\text{.}$$ (Equation 11)

To model the effect of testing, we define the matrix $diag\left(\text{FOR}\left(\text{x}\right)\right)$ with the state-dependent false omission rates $\text{FOR}\left(\text{x}\right)$ as its diagonal entries:

$$diag\left(\text{FOR}\left(\mathbf{x}\right)\right)=\left(\begin{array}{lll}\ddots \hfill & \hfill & \hfill \\ \hfill & \text{FOR}\left(x_{j,i}\right)\hfill & \hfill \\ \hfill & \hfill & \ddots \hfill \end{array}\right)\text{.}$$ (Equation 12)

The false omission rates themselves depend on the clinical specificity and sensitivity of the diagnostic test being used. Individuals in the pre-detection phase are—or will become—infectious, but are not detectable yet. Therefore, we define $\text{FOR}\left(x_{j,i}\right)=\text{specificity}\cdot x_{j,i}$ for nodes belonging to the pre-detection phase (j = 1, 2). Nodes in the post-detectable phase are not infectious anymore, hence $\text{FOR}\left(x_{j,i}\right)=0$ for the post-detectable phase (j = 5). For all other nodes, we have $\text{FOR}\left(x_{j,i}\right)=\left(1-\text{sensitivity}\right)\cdot x_{j,i}$.

The state probabilities at the end of an intervention $t_{end}$ can then be determined by:

$$p_{t_{end}}\left(\text{x}|\text{NPI}\right)=\left(\prod _{i}diag\left(\text{FOR}\left(\mathbf{x}\right)\right)\cdot e^{\Delta t_i\cdot A\left(SCR,f_s\right)}\right)\cdot e^{\left(t_{end}-t_n\right)\cdot A\left(SCR,f_s\right)}\cdot p_{t_0}\left(\mathbf{x}\right)\text{,}$$ (Equation 13)

where $\Delta t_i\in \left[t_1,t_2-t_1,\dots t_n-t_{n-1}\right]$ denotes the time spans between the start of the quarantine/isolation and the first test at time $t_1$ and between any two consecutive tests until $t_n$ (last test). The residual risk is then determined by computing:

$$p_{\infty }\left(\tilde{\text{x}}|\text{NPI}\right)=e^{s\cdot \tilde{A}(False,f_S)}\cdot \left(\begin{array}{c}{p}_{t_{end}}\left(\mathbf{x}|\text{NPI}\right)\\ 0\end{array}\right);s\to \infty \text{,}$$ (Equation 14)

and given by the last entry of the derived vector, i.e., $p_{\infty }\left({\tilde{\text{x}}}_{N+1}|\text{NPI}\right)$ as outlined above.

Prevalence estimation

The proposed model can also be used to estimate the prevalence from a user-provided incidence history. In addition to being informative in their own right, prevalence estimates can be used to evaluate NPI strategies for, e.g., incoming travelers. In doing so, we assume that an incoming traveler is exposed to the history of infection risks that the model user provides. These risks may relate to incidence reports from the country of origin of an incoming traveler, or they may relate to a mixture of exposure risks before and during traveling.¹⁰⁵ This allows one to (1) calculate the initial risk of infection at the moment of entry and (2) assess whether an individual is more likely to have acquired the infection recently or in the past.

To calculate the initial risk of infection at the moment of entry (the prevalence), we use the infection dynamics from Equation 7 together with the incidence reports of the preceding weeks and the probability of case detection/reporting, $P\left(\text{detect}\right)$, for the country or setting of interest. Using these factors we can calculate the probability distribution over the different model compartments at the time of travel$t_{\text{entry}}$ as:

$$p_{t_{\text{entry}}}\left(\mathbf{x}\right)=\sum _{s=-T}^{t_{\text{entry}}}{e}^{\left(t_t-s\right)\cdot A(False,f_s)}\cdot p_s\left(\mathbf{x}\right)\text{,}$$ (Equation 15)

where ($-T)$ is the time horizon before the date of travel. We evaluate the preceding 5 weeks. Five weeks was shown to be a sufficient time horizon to capture the dynamics of the model. The initial condition $p_s\left(\mathbf{x}\right)$ for $s$ days prior to the date of travel is computed from the user-provided incidence history and corrected for $P\left(\text{detect}\right)$. Weekly incidence numbers are uniformly distributed over the days of the week, e.g., to account for within-week reporting delays. For example, if $s\in$ week 3 prior to the week of travel, then:

$$\sum _{j=1}^4{p}_s\left(x_j\right)=\frac{{\pi }_{-\text{Δ}{w}_3}\left(\text{infect}\right)}{7\cdot P\left(\text{detect}\right)}\text{,}$$ (Equation 16)

where ${\pi }_{-\text{Δ}{w}_3}\left(\text{infect}\right)$ denotes the number of reported cases per week and per 100,000 inhabitants (the incidence) in week 3 prior to the week of travel. The individual probabilities assigned to the different phases are distributed according to the duration of the distinct phases:

$$\frac{p_s\left(x_j\right)}{{\sum }_{j=1}^4{p}_s\left(x_j\right)}=\frac{{\tau }_j}{{\sum }_{j=1}^4{\tau }_j}\text{,}$$ (Equation 17)

where ${\tau }_j$ denotes the mean residence time in phase $j$. The probabilities within the sub-compartments of each phase are uniformly distributed.

Parameter estimation

We estimated the number of sub-compartments per phase and the mean residence time per phase (model parameters $n_j$ and ${\tau }_j$) simultaneously from clinical time-course data in three steps (also see Table 2). First, parameters of the incubation phase (=pre-detection + pre-symptomatic, $j=\mathrm{1,2}$; compare Table 2) of the model are fitted. For this, we use a meta-analysis by Wei et al.⁶⁴ that encompasses 56 studies on the incubation period of SARS-CoV-2. Subsequently, the optimal parameters for the symptomatic phase of the model ($j=3$) are estimated independent of those of the incubation phase. We estimate the parameters based on the consensus of five studies that report on viral load, Ct values, and relative infectivity, three of which are published,65, 66, 67 in addition to in-house data (supplemental information) and data that have been kindly provided to us by the Consultant Laboratory for Coronaviruses Germany (Drosten Lab Charite Berlin) (T.C. Jones, personal communication). Last, the parameters of the post-infectious phase of the model ($j=4$) are estimated. We fix the estimated parameters for the proceeding three phases, $j=\mathrm{1,2,3}$, and fit the total model to the time-dependent PCR sensitivity profile reported by Kucirca et al.,⁶⁸ as well as the decrease in detection probability from symptom onset, as reported in Borremans et al.,⁶⁹ effectively estimating the mean residence time in the post-symptomatic phase. The procedure and the resulting parameters are depicted in Table 2.

Incubation (time to symptom onset)

We first estimate the parameters of the incubation phase based on the cumulative distribution of the time to symptom onset for general transmission reported by Wei et al.⁶⁴ In our modeling framework, the cumulative distribution of time to symptom onset is captured by $1-\sum _{j=1}^2{p}_t\left(x_j\right)$. To estimate the model parameters of the incubation period, we fit our model in the temporal range $t\in \left[\mathrm{0,30}\right]$ days post-infection to the reported mean cumulative distribution $y_t$. We then optimize the arguments $n_1,{\tau }_1$, and ${\tau }_2$ by minimizing the squared deviation of our model predictions, $\sum _{j=1}^2{p}_t\left(x_j\right)$, in the following sense:

$$n_1^{\ast },{\tau }_1^{\ast },{\tau }_2^{\ast }=argmi{n}_{n_1,{\tau }_1,{\tau }_2}{\left(y_t-\left(1-\sum _{j=1}^2{p}_t\left(x_j\right)\right)\right)}^2\text{,}$$ (Equation 18)

with initial conditions $p_0\left(x_{\mathrm{1,1}}\right)=1$ and $p_{t_0}\left(x_{j,i}\right)=0$ for all $\left(j,i\right)\ne \left(\mathrm{1,1}\right)$. Fixing $n_2=1$ (compare Table 1), we obtain the optimal parameters $n_1^{\ast }=5,{\tau }_1^{\ast }=2.86,{\tau }_2^{\ast }=3.91$. In addition to the results derived in the original study,⁶⁴ this procedure estimates which parts of the mean incubation period reported by Wei et al. (6.9 days) are, on average, spent in the pre-detection phase and in the pre-symptomatic phase. To estimate lower and upper extreme values for ${\tau }_1$ and ${\tau }_2$, we fix $n_1=5$, as well as the ratio between the residence time of the pre-detection phase and the total incubation period from the default parameters, ${\tau }_1=0.442\cdot \left({\tau }_1+{\tau }_2\right)$. We then optimize ${\tau }_1^{upper/lower}$ and ${\tau }_2^{upper/lower}$ for the minimum least-squares deviation between the model prediction and respectively the lower and upper bounds reported by Wei et al.⁶⁴ From this we obtain ${\tau }_1^{upper/lower}=(2.38,3.37)$ and ${\tau }_2^{upper/lower}=(3.27,4.62)$ days.

Infectiousness after symptom onset

Next, we estimate parameters of the infectious phase after symptom onset (or peak virus load) from viral load kinetics by Ejima et al.,⁶⁷ van Kampen et al.,⁶⁶ Jones et al. (personal communication), and in-house data (supplemental information) and based on the relationship between culture positivity and time since symptom onset reported by Singanaygam et al.⁶⁵

The in-house Ct values are transformed to viral kinetics using the methods exemplified in the analysis of infectivity profiles in the supplemental information. For each dataset, we fit a linear equation to the reported log₁₀ viral kinetics. We first use a sliding window technique (window size of 30 consecutive data points) to extract the average slope of the log₁₀ viral load values to which we then fit a linear equation by minimizing the least-squares deviation, similar to the method exemplified in the supplemental information. For each fit, the slope $a$ and intercept $b$ are used to simulate viral load data in the temporal range $t\in \left[\mathrm{0,21}\right]$ using:

$${\log }_{10}\left(VL\left(t\right)\right)=-t\cdot a+b+\epsilon \text{,}$$ (Equation 19)

where $\epsilon \sim \mathcal{N}(0,{\sigma }^2)$ is an additive error. The simulated viral loads in turn are used to construct relative infectivity profiles based on the attack rate curve as exemplified in the supplemental information, using the optimal parameters for the attack rate curve $z_t$ reported therein.

In our model, such relative infectivity profiles are captured by $p_t\left(x_3\right)$, when using initial conditions $p_{t_0}\left(x_{\mathrm{3,1}}\right)=1$ and $p_{t_0}\left(x_{j,i}\right)=0\forall \left(j,i\right)\ne \left(\mathrm{3,1}\right)$. The symptomatic infectious phase of the model is fit to each relative infectivity dataset $d$ separately, by minimizing the sum of squared deviations. We enforce one global $n_3$ hyperparameter (number of sub-compartments in phase) for all dataset fits, while allowing distinct local optima for ${\tau }_{3_d}$ (the mean residence time):

$$n_3^{\ast },\left[{\tau }_{3_{d_1}}^{\ast },{\tau }_{3_{d_2}}^{\ast },{\tau }_{3_{d_3}}^{\ast },{\tau }_{3_{d_4}}^{\ast },{\tau }_{3_{d_5}}^{\ast }\right]=argmi{n}_{n_3}argmi{n}_{{\tau }_{3_{d_1}},{\tau }_{3_{d_2}},{\tau }_{3_{d_3}},{\tau }_{3_{d_4}},{\tau }_{3_{d_5}}}\sum _d\frac{{\left(z_t-p_t\left(x_3;n_3,{\tau }_{3_d}\right)\right)}^2}{N_d}\text{,}$$ (Equation 20)

where$N_d$ is the number of observations in the respective dataset $d$. We obtain optimal parameters $n_3=13$ and ${\tau }_3=7.5$ (taken to be the median of the five fitted values for the individual studies). To estimate lower and upper extreme values for${\tau }_3$, we fix $n_3=13$ and minimize the least-squares deviation for the lower and upper bounds of the error range of all five data upper/lower bounds combined. From this, we estimate ${\tau }_3\in (2.79,11.47)$. In Figure S2A, we show the optimization of parameter $n_3$, whereas Figure S2B–S2F depicts the fits to the individual studies.

Time-dependent assay sensitivity and detection probability for PCR assay

Currently, PCR-based diagnostic tests are the gold standard for detecting a SARS-CoV-2 infection. Since the utilized primers are highly specific for SARS-CoV-2, we use a clinical specificity ($Spec$) of $0.999$. The PCR also has an analytical sensitivity of nearly $100\%$ if sufficient viral material is contained in the sample. The clinical sensitivity, however, depends on time since infection and is capped at a maximum sensitivity:⁶⁸

$$Sen{s}_{max}=\underset{t}{\max }\left[P_t\left(PC{R}^{+}|SARSCoV{2}^{+}\right)\right]\approx 80\%\text{.}$$ (Equation 21)

While the former is a result of the viral dynamics, the latter has to do with the pre-analytics, i.e., whether the health personnel are able to get hold of sufficient viral material during swab sampling. Because the model is developed primary for comparing NPI strategies for the public, samples for PCR tests are assumed to be from the upper respiratory tract.

The mean residence time in the post-infectious phase ${\tau }_4$ is estimated with the maximum sensitivity as an input parameter, such that the temporal change in the false omission rate,⁶⁸ as well as the decrease in detection probability from symptom onset,⁶⁹ is captured sufficiently.

To estimate the optimal ${\tau }_4$ value, we fix the optimal parameters for all previous phases and set $n_4=1$. The time-dependent assay false omission rate is computed as:

$$FO{R}_t=Spec\cdot p_t\left(x_1\right)+\left(1-Sen{s}_{\text{max}}\right)\cdot \sum _{j=2}^4{p}_t\left(x_j\right)\text{,}$$ (Equation 22)

with $p_{t_0}\left(x_{\mathrm{1,1}}\right)=1$ and $p_{t_0}\left(x_{j,i}\right)=0\forall \left(j,i\right)\ne \left(\mathrm{1,1}\right)$. The relative detection probability from symptom onset is computed as:

$$P_t\left(detect\right)=\frac{\left(1-diag\left(FOR\left(\mathbf{x}\right)\right)\right)\cdot e^{t\cdot A}\cdot p_{t_0}\left(\mathbf{x}\right)}{\left(1-diag\left(FOR\left(\mathbf{x}\right)\right)\right)\cdot e^{t_0\cdot A}\cdot p_{t_0}\left(\mathbf{x}\right)}\text{,}$$ (Equation 23)

with $p_{t_0}\left(x_{\mathrm{3,1}}\right)=1$ and $\left(x_{j,i}\right)=0\forall \left(j,i\right)\ne \left(\mathrm{3,1}\right)$. We estimate ${\tau }_4$ by simultaneously fitting $P_t\left(detect\right)$ to the detection probability profile for the upper respiratory tract⁶⁹ and to the temporal PCR false omission rate profile $FO{R}_t$ published by Kucirca et al.⁶⁸ in a least-squares sense. This gives us ${\text{τ}}_4=8$ days. We fit no upper and lower bounds for ${\tau }_4$.

Antigen-based rapid diagnostic tests

RDTs through antigen detection are currently in development. Early validation results from two commercially available products compared their analytic performance with PCR.¹⁰⁶ In summary, the antigen tests show a comparable sensitivity with respect to PCR for samples with low Ct values (high virus content in sample) and appear to be less sensitive at high Ct values (low virus content in sample).^84,85,107 Overall, sensitivities of P(RDT⁺|PCR⁺) = 85%–89% with respect to PCR were reported for the two evaluated testing systems. Specificity was 99.7%–100% with respect to PCR. Since no data about the temporal changes in this relative sensitivity are available to date, we assumed it to be comparable to the PCR and calculated the maximum sensitivity of RDT assays as:

$$\begin{array}{l}Sen{s}_{\text{max}}=\underset{t}{\max }[P_t({\mathrm{RDT}}^{+}|\mathrm{SARSCoV}{2}^{+})]\\ =\underset{t}{\max }\left[P({\mathrm{RDT}}^{+}|{\mathrm{PCR}}^{+}\right)\cdot P_t\left({\mathrm{PCR}}^{+}|\mathrm{SARSCoV}{2}^{+})+P({\mathrm{RDT}}^{+}|{\mathrm{PCR}}^{-}\right)\cdot P_t\left({\mathrm{PCR}}^{-}|\mathrm{SARSCoV}{2}^{+}\right)]\\ \approx 70\%\end{array}$$ (Equation 24)

We provide the model as a user-friendly software in an associated descriptor article,⁶³ which enables decision-makers to assess arbitrary NPI strategies. The software allows full flexibility with regard to parameter choices and strategy design. The default parameters of the software are set to the parameters estimated above.

Published: April 20, 2021