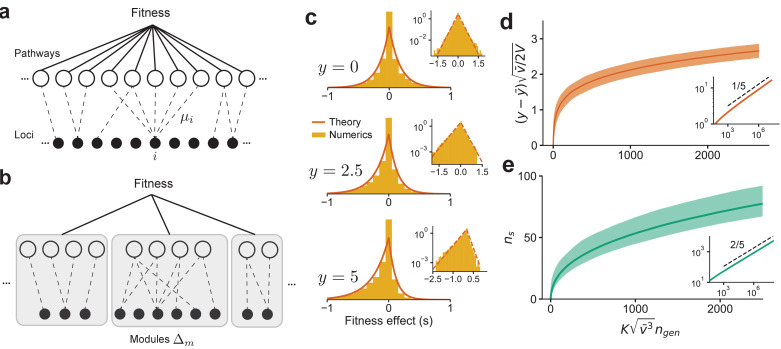
Figure 4. The distribution of fitness effect (DFE) and long-term adaptation dynamics predicted for the connectedness model.

(a) Schematic of the connectedness (CN) model, where each locus is associated with a fraction µ of pathways that contribute to the organism’s fitness. (b) An alternative model with modular organization, where sets of loci interact only within the pathways specific to a single module. (c) The DFE predicted from Equation (14) matches those obtained from simulated evolution of genotypes from the CN model. 128 randomly drawn genotypes (400 loci) with initial fitness $y$ close to zero are evolved to $y=2.5$ and $y=5$, and the DFE is measured across loci and genotypes. We chose $\overline{y}=0$ and $V=1$ so that $y$ represents adaptedness. Insets: same plots in log-linear scale. Note that the number of beneficial mutations acquired during the simulated evolution ($\sim$10-20) is much less than the total number of loci (400). (d) For a neutrally adapted organism, the theory predicts quick adaptation to a well-adapted state beyond which the adaptation dynamics are independent of the specific details of the genotype-fitness map. Shown here is the mean adaptation curve predicted under strong-selection-weak-mutation (SSWM) assumptions, which leads to a power-law growth of fitness with exponent 1/5 in the well-adapted regime (inset). (e) The number of fixed beneficial mutations under SSWM, which grows as a power-law with exponent 2/5 in the well-adapted regime (inset). The shaded region is the 95 confidence interval around the mean for (c) and (d). See Materials and methods and SI for more details.