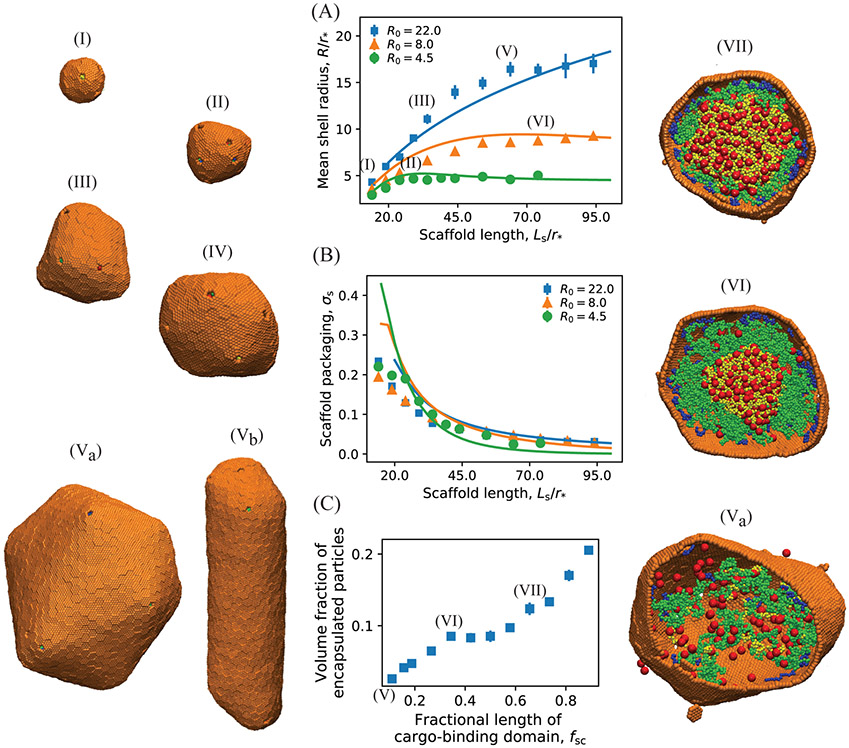
Figure 3:

(A) The mean shell radius as a function of the scaffold length calculated from Brownian dynamics simulations (symbols) and the equilibrium theory (Eq. 1, lines). Results are shown for different shell spontaneous curvature radii: R₀ = 4.5(●), 8.0(▲), 22.0(■). Example snapshots of assembled shells are shown to the left, taken from simulations with (I): R₀ = 22, L_s = 14, (II): R₀ = 8, L_s = 24, (III): R₀ = 22, L_s = 34, and (IV): R₀ = 8, L_s = 74, (V_a,b): R₀ = 22, L_s = 64. (B) Dependence of scaffold packaging on scaffold length and shell spontaneous curvature. The scaffold surface density (or ratio of packaged scaffold molecules to shell subunits, σ_s ≡ n_scaf/n_shell) is shown for the same parameter values as in (A). In (A) and (B) the length of the middle domain of the scaffolds L_sm is varied, with fixed shell-interacting and cargo-interacting domain lengths L_sh = 7 and L_sc = 7. The lines correspond to numerical minimization of Eq. 1, with respect to $L_{\mathrm{s}}\sim R_{\text{scaf}}^2$ and σ, with the scaffold chemical potential as an adjustable parameter set to Δμ = −2.5k_BT. Other theory parameters are taken from the simulations: the scaffold bead excluded volume $v=0.065r_{\ast }^3$ and $a\kappa =12.5k_{\mathrm{B}}T{r}_{\ast }^2$ (with a the subunit area and κ the bending modulus, which was approximately determined in Ref. 47). (C) Dependence of the volume fraction of encapsulated particles (cargo and scaffolds) on the fractional length of cargo-binding domain of scaffolds f_sc = L_sc/L_s, for R₀ = 22, L_s = 64, and L_sh = 7. Snapshots of the interior of shells assembled at different parameter values are shown on the right: (V_a): f_sc = 0.11, (VI): f_sc = 0.27, (VII): f_sc = 0.58. Other parameter values for (A), (B) and (C) are as follows. Shell subunit-subunit affinities: ε_hh = 3.15 at R₀ = 4.5, ε_hh = 2.85 at R₀ = 8.0 and ε_hh = 2.65 at R₀ = 22; scaffold-shell interaction ε_sh = 2.5, and scaffold-cargo interaction ε_sc = 1.0.