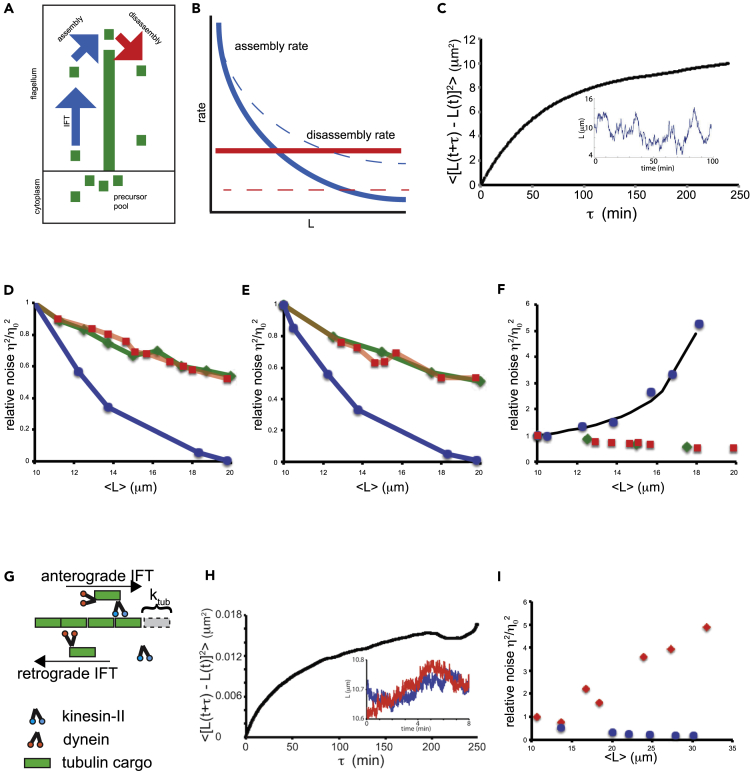
Figure 5.

Model predictions for noise versus length

(A) Schematic of balance-point mode for flagellar length control. Flagellar microtubules undergo constant disassembly (red arrow) at a length-independent rate D. This disassembly is balanced by assembly, which occurs at a rate limited by the rate of IFT (blue arrow). The rate of IFT entry is proportional to 1/L based on experimental measurements (Engel et al., 2009). Precursor protein from the cytoplasm binds with first-order binding. The available free precursor pool is the total pool P minus the quantity of precursor already incorporated into the two flagella. Hence the net assembly rate is given by A(P-2L)/L.

(B) Steady-state length is determined by the balance point between length-independent disassembly (red line) and length-dependent assembly (blue line). Mutations can increase flagellar length either by increasing assembly (blue dotted line) or by decreasing disassembly (red dotted line).

(C) Simulation results for the balance point model in which a Gaussian perturbation is added to the net rate of assembly (see methods). The resulting plot of mean-squared change in length versus time interval has a similar form to experimental observations. Inset shows a typical simulation trace of length versus time.

(D) Results of applying fluctuations to the disassembly rate D. Graph shows three curves, each representing a parameter change that increases the average length. For each curve, one parameter (A, D, or P) was varied, the average length determined, and then the uncorrelated variation computed by stochastic simulations in which a Gaussian perturbation was applied to the assembly parameter D. The Y axis of the graph plots the uncorrelated length variation (here denoted η²) normalized by the uncorrelated variation denoted obtained in simulations using the wild-type values of the three parameters (denoted η₀²). This normalized noise is unitless. Parameter values for the wild-type case are those previously derived from experimental measurements (Marshall and Rosenbaum, 2001). (Blue circles—length increased by decreasing D; red squares—length increase by increasing A; green diamonds—length increase by increasing P).

(E) Results of applying fluctuations to the assembly coefficient A. Again the three curves show the normalized uncorrelated variation as a function of flagellar length as each of the three parameters is changed so as to cause an increased length. (Blue—length increased by decreasing D; red—length increase by increasing A; green—length increase by increasing P).

(F) Results of stochastic simulation of the balance point model in which the three parameters A, D, and P are held constant, but noise is applied to the net rate of assembly obtained from the balance point model at each time point. As with panels D and E, the three model parameters were changed to increase average length and the normalized uncorrelated variation plotted. (Blue—length increased by decreasing D; red—length increase by increasing A; green—length increase by increasing P). The black line included in this plot shows the analytical prediction of a small signal noise analysis assuming an intrinsic noise source acting within one flagellum, given in the text as Equation 5.

(G) A length control model based on diffusive return of IFT kinesin (Hendel et al., 2018).

(H) Stochastic simulation of the diffusion-based model showing that the diffusion model recapitulates a mean-squared change in length versus time lag curve that resembles a constrained random walk-like behavior. Inset shows sample traces of two flagella simulated in a cell.

(I) Uncorrelated variation as a function of average length in the diffusion model. As with panels D–F, uncorrelated variation is normalized by the value seen with parameters giving wild-type length. (Blue) Variation of the build-size parameter reflecting the length increment per arrival of cargo. (Red) variation of the disassembly rate parameter reflecting the steady-state rate of tubulin removal from the tip.