A Predictive 3D Multi-Scale Model of Biliary Fluid Dynamics in the Liver Lobule

SUMMARY

Bile, the central metabolic product of the liver, is transported by the bile canaliculi network. The impairment of bile flow in cholestatic liver diseases has urged a demand for insights into its regulation. Here, we developed a predictive 3D multi-scale model that simulates fluid dynamic properties successively from the subcellular to the tissue level. The model integrates the structure of the bile canalicular network in the mouse liver lobule, as determined by high-resolution confocal and serial block-face scanning electron microscopy, with measurements of bile transport by intravital microscopy. The combined experiment-theory approach revealed spatial heterogeneities of biliary geometry and hepatocyte transport activity. Based on this, our model predicts gradients of bile velocity and pressure in the liver lobule. Validation of the model predictions by pharmacological inhibition of Rho kinase demonstrated a requirement of canaliculi contractility for bile flow in vivo. Our model can be applied to functionally characterize liver diseases and quantitatively estimate biliary transport upon drug-induced liver injury.

Graphical Abstract

In Brief

Meyer et al. developed a 3D multi-scale model of biliary fluid dynamics in the mouse liver lobule to predict drug-induced alterations of bile flow. They demonstrate two inversely related gradients of bile velocity and pressure in the lobule and show that bile flow is driven by the osmotic effects of bile secretion and bile canaliculi contractility.

Graphical Abstract

INTRODUCTION

The bile canaliculi network of the liver transports bile to the intestine for the digestion of nutritional lipids and clearance of metabolic waste products. Due to the detergent-like properties of bile, cholestasis, the impairment of bile flow, induces hepatocellular damage from extracellular accumulation of bile acids, fibrosis, and ultimately cirrhosis under chronic conditions (Balistreri et al., 2005; Boyer, 2013; Coleman et al., 1979; Padda et al., 2011; Trauner et al., 1998). The detoxifying function of the liver renders the organ prone to drug-induced liver injury (DILI) (Giri et al., 2010). DILI therefore represents a prevalent problem of pharmacological drug development.

Current diagnostic techniques for DILI and cholestasis are based on the detection of serum markers and imaging methods such as computer tomography. However, these have low resolution and only provide a limited understanding of the underlying disease etiology. Biomedical investigations of cholestatic liver disease and pharmacological drug safety assessments therefore require a quantitative understanding of biliary fluid dynamics to study and target the regulation of bile flow. Yet, despite its importance, experimental measurements or computational simulations of intrahepatic bile flow are currently unavailable.

Bile canaliculi are subcellular structures of 0.5–2 μm in diameter. They are formed by the apical membranes of counter-and juxtaposed hepatocytes that collectively build a highly ramified 3D tubular network (Elias, 1949). Bile, which is generated by apical secretion from hepatocytes, flows from the central vein (CV) to the portal vein (PV) area of the liver lobule, where it drains into the common bile duct (Elias, 1949). Blood flows counter current through the sinusoidal endothelial network, from PV to CV. Along this porto-central axis, the biliary network displays geometrical and functional differences, including bile canaliculi branching frequency, diameter, and hepatocyte bile acid transport activity (Baumgartner et al., 1986, 1987; Layden and Boyer, 1978; Morales-Navarrete et al., 2015). Due to these heterogeneities, the measurement and simulation of intrahepatic biliary fluid dynamics require a quantitative approach that considers spatial differences and that bridges the micrometer (subcellular) to the millimeter (lobule) scale.

To gain insights into the regulation of the biliary transport system, we combined intravital microscopy (IVM) of bile flux with multi-resolution 3D analysis of bile canaliculi network geometry to develop a predictive multi-scale model of biliary fluid dynamics of the adult mouse liver. Our results reveal new insights into the functional and structural heterogeneity of the biliary network within the liver lobule, demonstrate the occurrence of canalicular peristalsis as a determinant of bile flow, and provide a tool to analyze bile transport under disease conditions.

RESULTS

General Strategy of a 3D Multi-scale Model of Biliary Fluid Dynamics

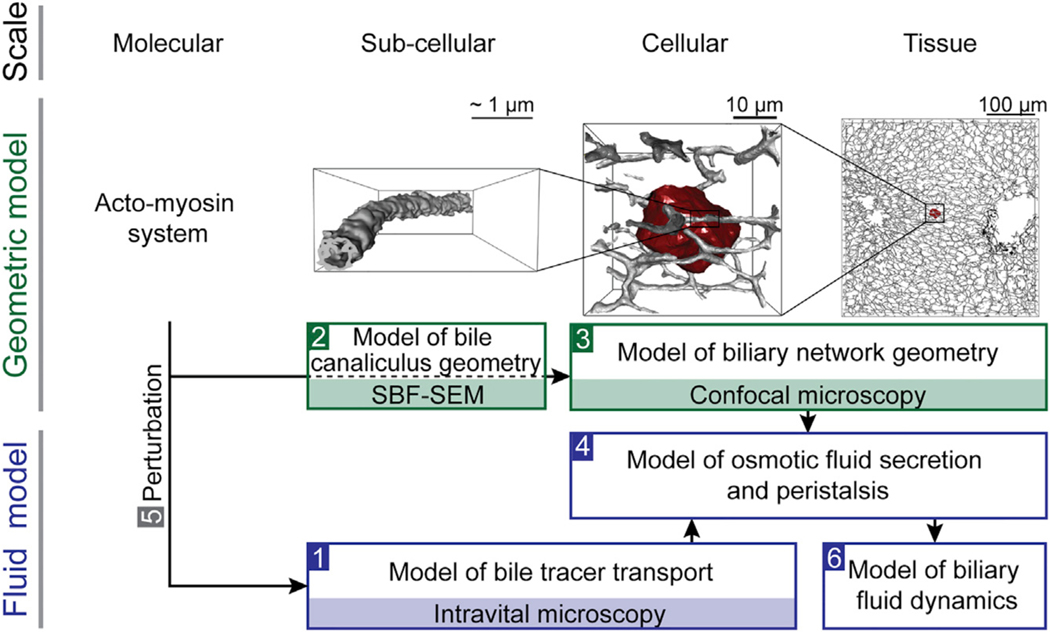
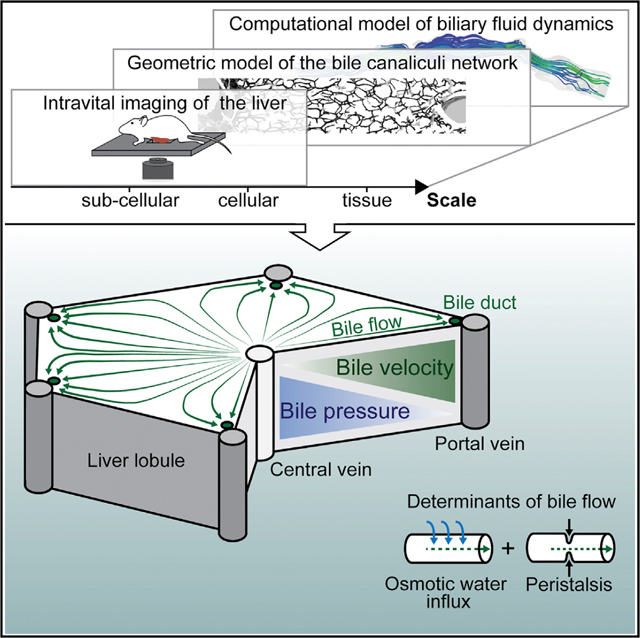
Bile canaliculi form a contiguous tubular network throughout the liver lobule that transports bile. Bile transport is generally thought to depend on the osmotic effect of bile secretion (Ballatori and Truong, 1989; Boyer and Bloomer, 1974; Boyer and Klatskin, 1970). However, a peristaltic mechanism has also been evoked (Oshio and Phillips, 1981; Watanabe et al., 1991). To simulate biliary fluid dynamics, we successively integrated the structural and functional properties of the bile canaliculi network from each level of organization, subcellular (i.e., the apical membrane of hepatocytes), cellular (the hepatocytes), and tissue (the bile canaliculi network within the lobule), into a 3D multi-scale model following the strategy schematically illustrated in Figure 1. First, we determined subcellular parameters of bile transport by IVM and mathematical modeling of a fluorescent bile tracer (step 1). Next, we complemented these functional measurements with quantitative models of bile canaliculi network geometry obtained from a combination of electron and confocal microscopy (steps 2 and 3). From these measurements, we determined the parameters of bile flow through the bile canaliculi network (step 4). Using pharmacological perturbation of actomyosin contractility, we determined the contribution of osmosis and peristalsis to biliary flow (step 5). Finally, we combined experimental and modeling results in a predictive tissue-scale model of biliary fluid dynamics (step 6).

Figure 1. Strategy of a Multi-Scale Model of Biliary Fluid Dynamics.

Strategy for the development of a multi-scale model of biliary fluid dynamics by integration of geometric (green) and fluid dynamic (blue) models from different scales. Bile canaliculi network organization: the actomyosin system (molecular scale) is a central component of the subapical cortex of hepatocytes (shown in red) that form bile canaliculi (shown in gray) from their apical membrane (subcellular scale). These build continuous belts in between neighboring hepatocytes (cellular scale) and a ramified tubular network throughout the liver (tissue scale). Modeling strategy: biliary transport properties were estimated from intravital microscopy of a bile tracer in a (sub)cellular model of bile transport (step 1). Next, geometric bile canaliculi properties were quantified from 3D models of the single bile canaliculus (step 2) and bile canaliculi network (step 3) using serial block-face scanning electron (SBF-SEM) and confocal microscopy. Based on these experimental measurements, parameters of bile flow were determined in a model of osmotic fluid secretion and biliary peristalsis (step 4) using molecular perturbation of the actomyosin machinery (step 5). The model result was applied to simulate biliary fluid dynamics at the tissue level (step 6).

Intravital Imaging of the Bile Tracer CFDA Reveals Heterogeneities of Hepatic Transport within the Liver Lobule

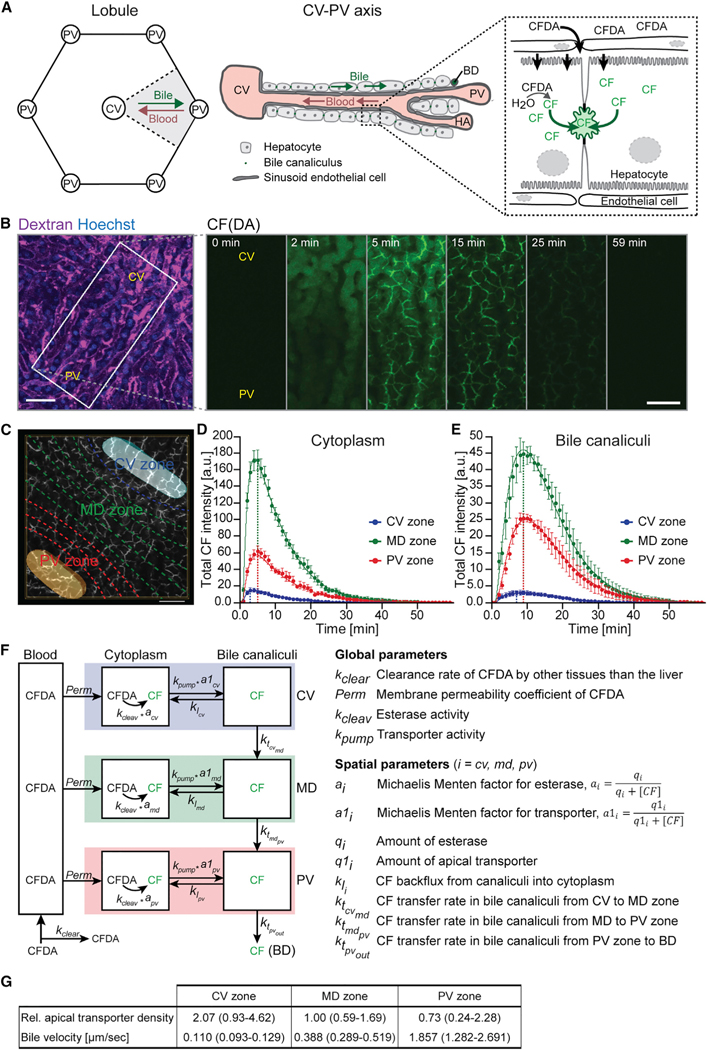
The osmotic effect of hepatocyte apical secretion represents the main determinant of bile flow. It depends on the secretion of bile salts (bile salt-dependent bile flow [BSDF]) (Boyer and Bloomer, 1974) and other organic molecules such as glutathione (bile salt-independent bile flow [BSIF]) (Ballatori and Truong, 1992; Boyer and Klatskin, 1970). Due to the functional zonation of the liver lobule (Baier et al., 2006; Berkowitz et al., 1995; Groothuis et al., 1982), an insight into the osmotic effects of bile secretion would require a spatially differentiated analysis of the collective apical transport activities of hepatocytes, which is currently impossible. In contrast to humans, in rodents BSIF contributes substantially to the total bile flow (Boyer, 2013; Erlinger, 1996). Therefore, to derive an estimate of apical bile secretion and bile velocity in the bile canaliculi network, we performed IVM of the well-established fluorescent tracer 6-carboxyfluorescein diacetate (CFDA) (Babbey et al., 2012; Breeuwer et al., 1995; Liu et al., 2007; Porat-Shliom et al., 2016). CFDA secretion depends on the apical multidrug resistance-associated protein 2 (MRP2) (Zamek-Gliszczynski et al., 2003), which primarily transports organic anions (BSIF) (Paulusma et al., 1999; Wielandt et al., 1999) and only to a minor extent glucuronidated bile acids (BSDF) (Akita et al., 2001). CFDA is a membrane-permeant molecule that becomes fluorescently excitable and membrane impermeable upon hydrolysis into 6-carboxyfluorescein (CF) by intracellular esterases (Breeuwer et al., 1995). Following intravenous (i.v.) injection, CFDA enters the liver lobule through the blood via the PV and drains into the CV. Along this porto-central axis, CFDA is taken up by hepatocytes, cleaved into its fluorescent derivative CF in the hepatocyte cytoplasm, actively secreted into the bile canaliculi by MRP2, and cleared from the system via the common bile duct (Figure 2A) (Babbey et al., 2012; Breeuwer et al., 1995; Zamek-Gliszczynski et al., 2003).

Figure 2. Quantification of Bile Transport by Intravital Imaging of CFDA.

(A) Schematic illustration of the liver lobule geometry and CF(DA) transport. In the lobule, blood flows from the portal vein (PV) to the central vein (CV). Bile flows counter current and drains into the bile duct (BD). CFDA is taken up by hepatocytes from the blood, cleaved into its fluorescent derivative CF in the cytoplasm, secreted into bile canaliculi, and transported through the bile canaliculi network via the bile flow. HA, hepatic artery.

(B) Representative images from an IVM movie showing the transport of CF(DA) within the CV-PV axis at indicated time points after acquisition start. CFDA was administered at 1 min. The approximate localization of the CV and PV was identified from the vascular flow patterns using fluorescent-conjugated dextran (magenta) and is indicated. Shown are maximum projections of 19-μm z stacks. Scale bar, 50 μm.

(C) Schematic illustration of the spatial analysis approach of CF transport from IVM movies. The localization of the CV (light blue) and PV (orange) was estimated from the vascular flow patterns, the CV-PV axis was computationally divided into ten equidistant areas (dashed lines), and the CF intensities were quantified in the CV (blue), MD (green), and PV (red) zones. Scale bar, 50 μm.

(D and E) Quantification of the total CF intensity in the hepatocyte cytoplasm (D) and bile canaliculi (E) from IVM movies as shown in (B), determined for the CV (blue), MD (green), and PV (red) zones. Dots represent experimental measurements (n = 4 mice, mean ± 68% confidence interval [CI]), and solid lines show the fit of the three-compartment model of CF(DA) transport shown in (F). Dashed lines indicate time points of maximum CF intensity.

(F) Schematic representation of the compartment model of CF(DA) transport in the liver. For model description, see text. Rate constants are described on the right. Model results are displayed as solid lines in (D) and (E).

(G) Relative apical transporter density and bile velocity estimated from IVM of CF transport using the model shown in (F). Transporter density was determined based on the kite-shaped geometry of the CV-PV axis and is expressed relative to the MD zone. n = 4, mean ± 95% CI.

See also Figures S1 and S2; Table S1; Movie S1.

To take into account heterogeneities of bile transport within the liver lobule, we imaged CFDA transport in a spatially resolved manner along the entire porto-central axis in adult mice (step 1 in Figure 1). A typical problem in such experiments is the artifacts introduced by motion. To minimize cardiac and respiratory motion artifacts, we embedded the organ in a water-based gel in a custom-designed microscope stage-insert (see STAR Methods and Porat-Shliom et al., 2016). Particular care was used to avoid artifacts caused by surgery and phototoxicity (see examples of tissue damage in Figures S1A and S1B). This is especially important when IVM is conducted under perturbations (see below). Our setup sustained physiological levels of blood flow and did not present evidence of apparent tissue damage in the exposed liver lobe, proving high stability without compromising tissue integrity. Remaining sample drift was corrected by development and implementation of new image-processing algorithms into the MotionTracking software (Morales-Navarrete et al., 2015) (http://motiontracking.mpi-cbg.de; see STAR Methods section “Correction and Quantification of IVM Movie Shift”).

To identify the CV-PV axis of a liver lobule, we visualized the direction of blood flow and sinusoid orientation by i.v. injection of fluorescent-conjugated dextran (Figure 2B). Following image acquisition start, CFDA was administered i.v. and detectable in the hepatocyte cytoplasm within seconds (Figure 2B and Movie S1). Subsequently, CF became visible in the bile canaliculi network within 3–5 min and was cleared from the system within ~40 min. Comparison of intracellular fluorescence intensities along the CV-PV axis 2 min after CFDA injection revealed that pericentral hepatocytes accumulated the tracer faster than periportal hepatocytes (Figure 2B). Such heterogeneities and the observed transport dynamics are in agreement with previous reports of CF(DA) transport in the liver (Babbey et al., 2012; Lin et al., 2016).

Bile Velocity Establishes a Gradient within the Portocentral Axis

To estimate bile transport rates, we quantified the tracer intensities from IVM movies and described its kinetics in a mathematical model (step 1 in Figure 1). To determine the spatial heterogeneities of CF(DA) transport, we computationally divided the porto-central axis into three zones, the central zone (CV) corresponding to approximately one cell layer, the middle (MD) zone, with about six cell layers, and the portal (PV) zone with about three cell layers (Figure 2C), similar to the metabolic zonation (Benhamouche et al., 2006; Jungermann, 1988; Jungermann and Kietzmann, 1996; Morales-Navarrete et al., 2015). Within each zone, we quantified the CF intensity in the hepatocyte cytoplasm and bile canaliculi. Both compartments were segmented automatically from IVM movies using an ad hoc developed algorithm implemented in the MotionTracking software (see Figure S1C and STAR Methods section “Quantification of CF Intensities from Intravital Movies”). As expected from the zonation of CF secretion and the direction of bile flow, CF was secreted and cleared faster in the bile canaliculi network in the CV zone than the MD and PV zones (Figures 2D and 2E).

Next, we described the tracer kinetics in a mathematical model formulated as a set of ordinary differential equations (ODE) to estimate bile transport rates (Figure 2F; see STAR Methods section “Mathematical 3-Compartment Model of CF(DA) Transport in the Liver”). The model distinguishes tracer transport for the CV, MD, and PV zones and considers the different sizes and contact interfaces of the kite-shaped CV-PV area of the lobule (see Figures 2A and S2A–S2C). The model considers that, within each zone, CF is transported sequentially from the blood into the hepatocyte cytoplasm and, from here, actively secreted into the bile canaliculi network. In addition, passive back flux from the bile canaliculi into the cytoplasm is included. While CFDA rapidly equalizes between blood and hepatocyte cytoplasm by passive diffusion (Breeuwer et al., 1995), the (fluorescent) cleaved form CF is membrane impermeant and requires active transport. Therefore, the model assumes that both esterase activity and apical secretion follow Michaelis-Menten kinetics. To consider potential zonation of intracellular esterases and CF apical transporters, the model accounts for spatially heterogeneous levels of both parameters. For the bile canaliculi compartment, the model considers that the networks of the three lobule zones are connected and that CF propagates from the CV to the MD and PV zone network via the bile flow. Finally, CF exits the bile canaliculi network from the PV zone via the bile duct. Fitting of the model to the experimental measurements of CF intensities (Figures 2D and 2E, solid lines) showed that hepatic CF transport differs significantly within the liver lobule (Figure 2G; see also Table S1). First, consistent with Lin et al. (2016), the density of apical CF transporters, and thus the apical secretion rate, was ~2.8-fold higher in the CV zone than in the PV zone. Second, bile velocity within the bile canaliculi network increased progressively from the CV to the PV zone. Across the long distance of the MD zone (about six cell layers in diameter), bile velocity raised gradually about 3.5-fold. In the distal periportal network, however, within a distance of only three cell layers, bile velocity increased dramatically 4.8-fold from 0.388 μm/s to 1.857 μm/s. These results demonstrate the quantitative differences of biliary fluid dynamics within the bile canaliculi network of the liver lobule.

A Mechanistic Model of Osmotic Fluid Secretion and Bile Flow

The osmotic effect on bile flow depends on the apical secretion of bile by hepatocytes and the geometry of the bile canaliculi network. To explain the gradient of bile velocity along the CV-PV axis, we estimated the spatial distribution of osmotic water influx into the bile canaliculi (step 4 in Figure 1) from measurements of bile canaliculi geometry (steps 2 and 3 in Figure 1) and hepatocyte apical CF secretion.

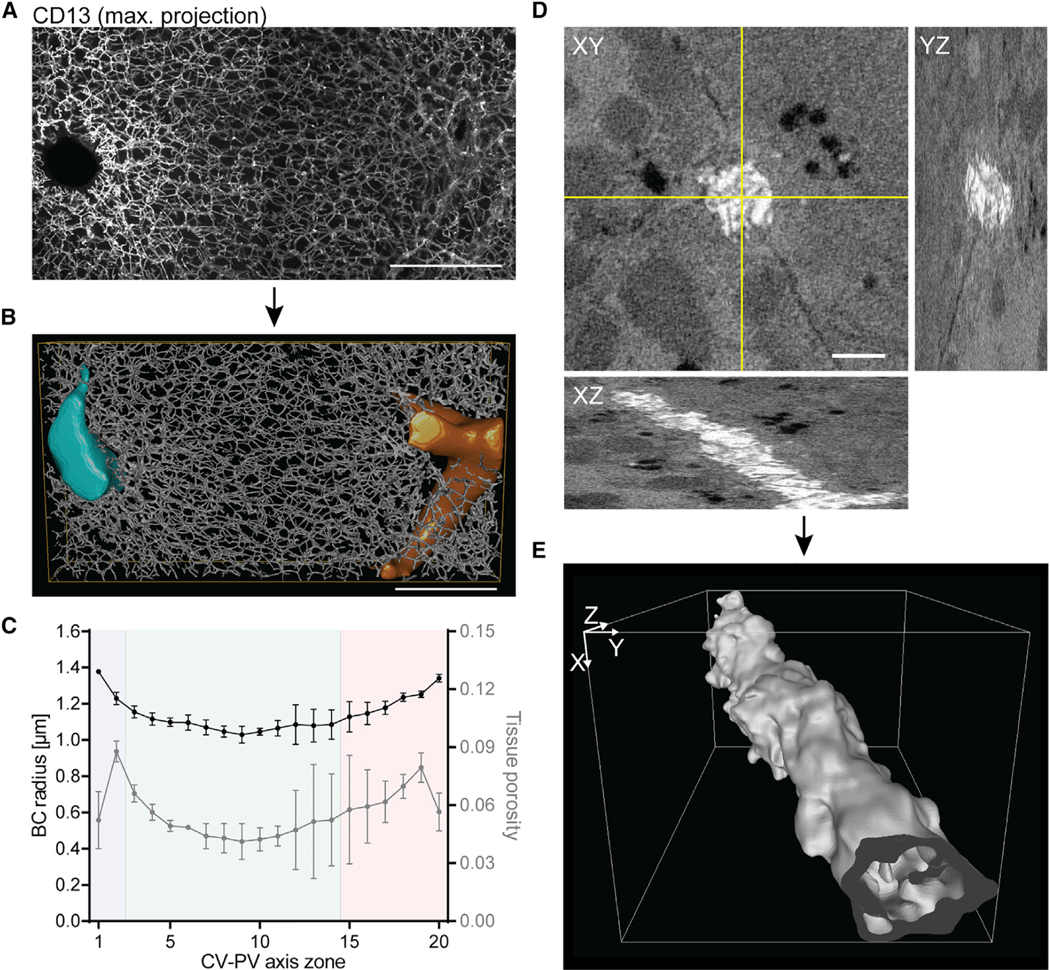
To determine the geometrical properties of the bile canaliculi network, we used our previously reported digital 3D model (step 3 in Figure 1 [Morales-Navarrete et al., 2015]). An important feature of this model is that it provides an accurate and spatially resolved estimate of the bile canaliculi network parameters that are crucial for the spatial fluid dynamics model. We reconstructed the bile canaliculi network from confocal images of immunostained thick liver tissue sections using the MotionTracking software (Morales-Navarrete et al., 2015). Sections were stained with the hepatocyte apical marker CD13 and an entire CV-PV axis was imaged as high-resolution z-stacks (approximately 400 × 230 × 80 μm in xyz dimension) (Figure 3A). Image stacks were used for 3D network reconstructions (Figure 3B) and the bile canaliculi radius was calculated for 20 zones along the CV-PV axis. The results demonstrate that the bile canaliculi radius is variable, being smallest in the middle of the CV-PV axis (1.03 ± 0.05 μm) and increasing up to 1.3-fold toward the CV and PV areas (Figure 3C, left y axis).

Figure 3. A Geometric Model of the Bile Canaliculi Network Reveals the Structural Heterogeneity within the Liver Lobule.

(A) Representative IF images of fixed mouse liver tissue sections stained for the apical marker CD13. Shown is a maximum projection of a 78-μm z-stack covering an entire CV-PV axis (CV to the left, PV to the right).

(B) 3D reconstruction of the bile canaliculi network shown in (A). The CV is shown in light blue, the PV in orange.

(C) Quantification of bile canaliculi radius (left y axis) and tissue porosity (right y axis) from reconstructions as representatively shown in (B). Quantification was performed for 20 equidistant zones along the CV-PV axis. Zones 1 and 20 are adjacent to the CV and PV, respectively, and displayed on the x axis. The blue, green, and red backgrounds indicate the localization of the CV, MD, and PV zones, respectively. n = 3 mice, mean ± SEM.

(D) Representative SBF scanning EM image stack of fixed mouse liver tissue. Shown is one xy plane of an 8-μm z-stack and yz and xz stack projections at the indicated lines (yellow).

(E) 3D reconstruction of the bile canaliculus shown in (D).

Scale bars, 100 μm (A and B) and 2 μm (D).

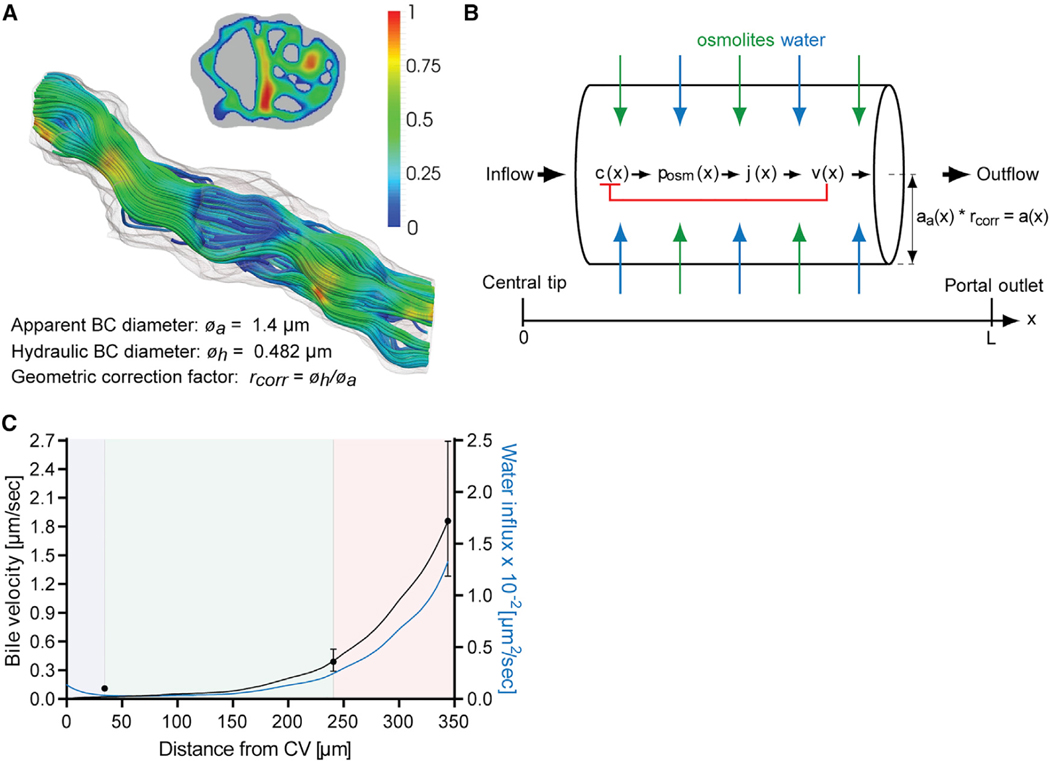
Importantly, bile canaliculi lumens are convoluted and densely packed with microvilli. Clearly such a micro-architecture is not resolvable by confocal microscopy, but affects coarse-grained fluid dynamic properties of bile flow such as friction. To account for this, we performed 3D electron microscopy (EM) analysis of liver tissue to reconstruct a bile canaliculus and calculate its hydraulic diameter, a measure for the cross-sectional flow in noncircular tubes (step 2 in Figure 1). We performed serial block-face (SBF) scanning EM (Deerinck et al., 2010), which allows for the automated image acquisition of relatively large volumes of tissue at nanometer resolution (12.4 nm pixel size, 40-nm steps in z dimension) (Figure 3D). Plane-wise manual segmentation of EM image stacks followed by 3D reconstruction and surface mesh generation using the Imaris software (BitPlane) visualized the dense packing of microvilli (Figure 3E). In the light of these structural features, bile canaliculi cannot be considered as smooth circular tubes in the model. To determine the relation between bile velocity and pressure within the reconstructed bile canaliculus, we numerically solved the Navier-Stokes equations in the 3D reconstructed bile canaliculus geometry. Simulations were carried out using the finite-volume method for physiologically relevant bile pressure conditions (10⁻³–10⁵ Pa). Bile is an incompressible Newtonian fluid with a viscosity similar to water (Luo et al., 2007). Given its low Reynolds number (Re ~ 10⁻⁶), bile flow can be considered to be laminar (see also STAR Methods section “Computational Fluid Dynamics Simulation of Bile Flow in a 3D EM-Reconstructed Bile Canaliculus”). From the simulations of bile flow in the reconstructed bile canaliculus (Figure 4A) we found a hydraulic diameter of 0.482 μm, which was significantly smaller than its average apparent diameter of 1.4 μm (as measured from EM images). Applying this ratio as a correction factor (r_corr = 0.344) to our confocal microscopy-based reconstruction, we derived realistic estimates of bile flow from the digital 3D geometric model.

Figure 4. A Mechanistic Model of Osmotic Fluid Secretion.

(A) Simulation of bile flow in the 3D geometry of the reconstructed bile canaliculus shown in Figure 3E. Bile velocity is expressed relative to the maximum and shown in the cross-sectional and longitudinal plane of the bile canaliculus. Values are color-coded as indicated by the legend. The bile canaliculus has a measured apparent diameter ø_a of 1.4 μm and a computed hydraulic diameter ø_h of 0.482 μm. The ratio of ø_h and ø_a defines the geometric correction factor r_corr that is used in the model of osmotic fluid secretion in (B).

(B) Mechanism of water influx into the bile canaliculi network for the model of osmotic fluid secretion. Schematic drawing of a bile canaliculus with apparent radius a_a(x), located between the tip of the bile canaliculi network in the CV area (left) and the outlet in the PV area (right). The radius a(x) = a_a(x) * r_corr is corrected for the hydraulic diameter of a bile canaliculus as determined in (A) using the correction factor r_corr. In the bile canaliculi network, bile is secreted and flowing along a series of branches with an average cumulative length L. The osmolite concentration profile c(x) generates the osmotic pressure surplus p_osm that drives water influx j(x) into the lumen. Osmotic pressure is counteracted by the local fluid pressure p(x) (not depicted) which is monotonously decreasing from a self-organizing pressure maximum at the closed tip to zero at the open outlet. As bile flows out with cross-section averaged velocity v(x), the osmolite concentration is diluted, representing a negative feedback loop between fluid flow and osmotic driving (red bracket).

(C) Prediction of the bile velocity (black, left y axis) and water influx density (blue, right y axis; unit: volume per time and per bile canaliculi length) into the bile canaliculi network along the CV-PV axis from the model of osmotic fluid secretion shown in (B). Solid lines show the model prediction, and dots (black) represent experimental measurements of bile velocity (n = 4, mean ± 95% CI) shown in Figure 2G. The blue, green, and red backgrounds indicate the localization of the CV, MD, and PV zones, respectively.

See also Table S2.

Based on our geometric model and IVM measurements of apical transport, we developed a mechanistic model of osmotic bile secretion and bile flow (step 4 in Figure 1). The model considers the measured heterogeneous bile canaliculi radius profile along the porto-central axis (Figure 3C), rescaled to the equivalent hydraulic radius, an average bile canaliculi path length of 344 μm between the CV and PV area (measured from the geometric model, Figure S2D), and the different sizes and interfaces of the zones within the kite-shaped CV-PV axis (Figure S2C) as well as previously reported fluid mechanic properties of bile (Luo et al., 2007; Mathias, 1985). Mechanistically, the model assumes that the secretion of osmolites into the bile canaliculi network generates an osmotic pressure that drives water influx and, consequently, bile flow (Figure 4B). The osmotic pressure is counteracted by the local fluid pressure and negatively regulated by the loss of osmolites from fluid outflow (Mathias, 1985). We solved the model analytically for steady-state flow conditions assuming zero flow at the origin of the network in the CV zone and zero pressure at the open outlet in the PV zone (see STAR Methods section “Mechanistic Model of Osmotic Fluid Secretion and Bile Flow”). The spatial profile of the bile flow velocity v(x) was obtained as a function of the measured bile canaliculi radius a(x) and the CV-PV axis distance L, and two parameters p₁ and p₂, representing combinations of material properties of the liver. The parameters p₁ and p₂ were determined by fitting the analytical function v(x) to the experimental data points (see Table S2). The resulting bile velocity and bile canaliculi network water influx profiles revealed an exponential-like increase from the CV to the PV area (Figure 4C). Overall, the model result reproduced well our IVM measurements in the MD and PV zones, but underestimated the pericentral bile velocity. This suggested that bile flow could be driven by an additional mechanism, e.g., bile canaliculi peristalsis (Oshio and Phillips, 1981; Watanabe et al., 1991). We therefore set out to test the function of peristalsis for bile flow and, finally, validate the predictive capacity of the model.

Bile Canaliculi Contractility Is a Determinant of Bile Flow

Earlier studies have provided evidence for bile canaliculi contractility in the rat liver in vivo at a speed of less than 1 μm per second, suggesting a function for bile flow (Oshio and Phillips, 1981; Watanabe et al., 1991). Given the low viscosity of bile, one would expect a much higher speed of the peristaltic waves if these were to act as a driving force of bile flow. Since, to our knowledge, no further studies have corroborated the contractile activity of bile canaliculi in vivo and provided evidence that it significantly contributes to bile flow, we set out to test this hypothesis.

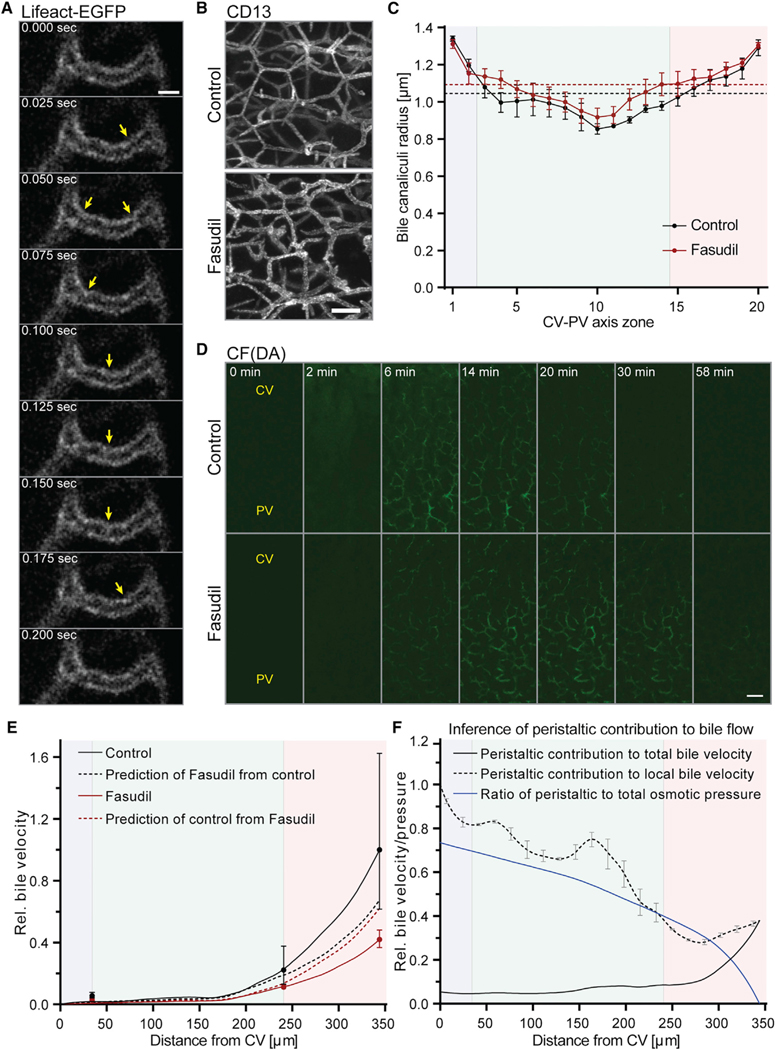
To verify that the biliary network has indeed contractile activity in vivo, we monitored the dynamics of bile canaliculi geometry by IVM of Lifeact-EGFP mice using the subapical actin mesh as bile canaliculi marker (Riedl et al., 2010). From cell culture studies, contractility of hepatocyte apical membranes has been shown to act in a calcium-dependent manner and, thus, suggested to be driven by calcium waves in vivo (Nathanson and Schlosser, 1996; Watanabe and Phillips, 1984; Watanabe et al., 1988). Given that calcium waves propagate at about 30 μm/s across the lobule (Nathanson et al., 1995), bile canaliculi peristalsis should occur at a similar speed, rendering its detection technically challenging. We therefore expected imaging at 0.025 s frame rate and 0.09 μm pixel size to be sufficient to capture only individual bile canaliculi constriction events of a peristaltic wave. Using these settings, we could indeed visualize contractile events occurring within a millisecond time frame (Figure 5A and Movie S2). To rule out motion artifacts, we determined the image shift of our IVM setup. Using second harmonic generation (SHG) imaging of elastin fibers of the liver capsule as stable reference structure, we found the shift to be ≤0.27 μm in xy over a time course of 0.5 min (Figures S3A–S3D), showing that contractility could be reliably measured for large bile canaliculi (diameter ≥2 μm). Thus, in contrast to a previous study, we found contractile events within the velocity range expected from the speed of calcium waves in the liver. Such contractility could indeed have a function for bile flow, as previously suggested (Watanabe et al., 1991).

Figure 5. Bile Canaliculi Contractility Is a Determinant of Bile Flow.

(A) Representative images from an IVM movie of a Lifeact-EGFP mouse liver showing the subapical F-actin belt of a bile canaliculus. Images were acquired at theindicated time points. Yellow arrows indicate bile canaliculus constriction events.

(B) Representative IF images of fixed liver tissue sections from control and fasudil-treated mice, stained for the apical marker CD13. Shown are maximum projections of ~75-μm z-stacks acquired in the PV area.

(C) Quantification of the bile canaliculi radius in control (black) and fasudil-treated (red) mice for 20 equidistant zones along the CV-PV axis. Zones 1 and 20 are adjacent to the CV and PV, respectively. Dashed lines represent the average network radius in control (black) and fasudil-treated (red) mice. n = 3 mice, mean ± SEM. Radius of control versus fasudil-treated mice, p > 0.05 (CV zone), p < 0.0001 (MD zone), p < 0.001 (PV zone).

(D) Representative images from IVM movies showing the transport of CF(DA) in the mouse liver of control or fasudil-treated mice at the indicated time points after acquisition start. CFDA was injected at 1 min. Shown are maximum projections of 17-μm z-stacks. The approximate localization of the CV and PV are indicated. Movies were acquired with identical imaging settings and are displayed with the same intensity threshold values.

(E) Test of the mechanistic model of osmotic fluid secretion. The model of osmotic fluid secretion was fit to experimental measurements of control (black solid line) and fasudil-treated mice (red solid line). From these model fits, bile velocity of fasudil-treated mice was predicted from the control condition (black dashed line) and bile velocity of control mice was predicted from fasudil-treated mice (red dashed line) (see text for detailed description). The velocity axis is relative to the value of the control condition in the PV area. Dots represent experimental measurements (control, black; fasudil, red). n = 4 mice (control), n = 5 mice (fasudil), mean ± 95% CI. Prediction of control from fasudil at PV outlet versus experimental measurement in control mice at PV outlet, p = 0.09; prediction of fasudil from control at PV outlet versus experimental measurement of fasudil-treated mice at PV outlet, p < 0.0001.

(F) Inference of the peristaltic contribution to bile flow. Shown is the peristaltic contribution to the total (black solid line) and local (black dashed line) bile velocity profile and to the total biliary pressure (blue solid line). The contribution to total bile velocity was inferred from the difference between the model prediction (E, red dashed line) and an empirical fit of the experimental control measurements (not shown in E). The local contribution of peristalsis to bile velocity was inferred from the ratio of the peristaltic contribution to the total bile velocity. Pressure is expressed relative to the maximum pressure obtained at the central tip. Error bars were propagated from the radius profile of control mice in (C). Peristaltic contribution to local bile velocity in CV versus PV zone, p < 0.0001.

The blue, green, and red backgrounds in (C), (E), and (F) indicate the localization of the CV, MD, and PV zones, respectively. Scale bars, 2 μm (A), 10 μm (B), and 25 μm (D). See also Figures S3 and S4; Movies S2 and S3; Tables S1 and S2.

Plasma membrane contractility is determined by the cortical actomyosin system (Sharanek et al., 2016; Tsukada and Phillips, 1993). Compromised actomyosin activity has been suggested as a candidate mechanism of cholestasis-inducing drugs (Sharanek et al., 2016). Consequently, inhibition of actomyosin contractility should affect biliary fluid dynamics. To test this prediction, we inhibited actomyosin activity pharmacologically using the Rho kinase inhibitor fasudil. Administration of 20 mg/kg fasudil for 1.5 hr resulted in a reduction of phosphorylated myosin light chain (pMLC) protein levels (Figure S4A), thus validating the inhibitory effect on Rho kinase activity. We next analyzed the bile canaliculi network geometry on fixed liver tissue sections and found a dilation of bile canaliculi in fasudil-treated mice (Figure 5B). Quantification of the bile canaliculi radius revealed that Rho kinase inhibition dilated bile canaliculi (Figure 5C). The radius was significantly increased by up to 12% in the MD (p < 0.0001) and 7% in the PV zone (p < 0.001) compared with control mice. This indicates that the diameter of the bile canaliculi network is regulated by the actomyosin system.

Finally, to determine the requirement of bile canaliculi contractility for bile flow, we tested the effect of Rho kinase inhibition on bile velocity by IVM of CF(DA) transport (step 5 in Figure 1). IVM of the bile canaliculi network in fasudil-treated mice revealed high sensitivity to phototoxicity and was only possible at minimum laser intensities and lower time intervals (2 min) compared with wild-type (WT) mice. Imaging of CF transport in fasudil-treated mice revealed that inhibition of myosin activity resulted in a marked delay of CF clearance from the bile canaliculi network (Figure 5D and Movie S3). We quantified a 50%–58% reduction of bile velocity across the CV-PV axis upon actomyosin inhibition in comparison with control mice (Figures 5E and S4B–S4E; Table S1). Unexpectedly, fasudil treatment also caused a reduction of apical CF transport (Figure S4F).

Using the mechanistic model of bile secretion and flow, we could now determine whether the osmotic effect is sufficient to explain the measured reduction of bile velocity upon perturbation by fasudil. Importantly, we took into account both the dilation of the bile canaliculi and the reduction of apical osmolite (CF) transport upon fasudil treatment. First, we determined the two parameters p₁ and p₂ of the osmotic model (see Table S2). To this end, we used the measured CV-PV axis distance L and the radius a(x) of control mice to fit p₁ and p₂ to the experimental data under control conditions (Figure 5E, solid black line). Keeping the axis distance L and p₂ constant, and using the experimentally measured bile canaliculi radius a(x) of fasudil-treated mice, we then predicted the bile velocity profile under fasudil treatment (Figure 5E, dashed black line). The value of p₁ was corrected to account for the change of osmolite secretion upon fasudil treatment (see STAR Methods section “Inference of Osmolite Concentration Changes and Prediction of Parameter Changes”). The same strategy was applied to fit the osmotic model parameters p₁ and p₂ to the experimental data under fasudil treatment (Figure 5E, solid red line) and predict the bile velocity profile under control conditions (Figure 5E, dashed red line; see also STAR Methods section “Inference of Peristaltic Contribution”). Both predictions deviated from the experimental measurements by ~45% in the PV zone. Despite considerable experimental variability in control mice, the difference between the model prediction and measured value under fasudil treatment in the PV zone is highly significant (p < 0.0001). Therefore, by proof by contradiction, we concluded that the contribution of peristalsis has a significant effect on bile flow.

Using our model, we estimated the contribution of peristalsis to biliary flow (Figure 5F). We defined the contribution of peristalsis to bile flow as the difference between the measured velocity profile under control conditions (where osmosis and peristalsis coexist, Figure 5E, solid black curve) and the velocity profile of osmotic driving alone. The latter was estimated in two steps. First, we fitted the parameters of the osmotic model to the measurements of bile velocity of fasudil-treated mice. Second, we used these parameters with the bile canaliculi radius profile and apical secretion rates under control conditions to predict the velocity profile of sole osmotic driving (Figure 5E, red dashed line; see STAR Methods section “Inference of Peristaltic Contribution”). The results suggest that peristalsis occurs particularly in the MD and PV zones, contributing up to 32% ± 3% (mean ± SD) of the total bile velocity in the PV zone (Figure 5F, black solid line). Considering the relative local contribution to velocity, peristalsis even accounts for 88% ± 6% (mean ± SD) of the velocity in the CV zone (Figure 5F, black dashed line). The local contribution is significantly higher in the CV than in the PV zone (p < 0.0001). This result could explain the underestimation of the measured bile velocity in the CV zone by the osmotic model (see Figure 4C). Next, we determined the relative contribution of peristalsis to bile pressure and found a monotonously decreasing spatial profile along the CV-PV axis (Figure 5F, blue line). Altogether our results reveal that, in addition to the well-established osmosis-dependent mechanism, actomyosin-driven contractility of the bile canaliculi network is a key determinant of bile flow.

Bile Velocity and Pressure Establish Two Opposing Gradients in the Liver Lobule

In the liver lobule, bile flow does not occur through a single linear tube but through a highly ramified 3D network. To consider this geometry, we integrated structural and fluid dynamic properties from the (sub)cellular level into a 3D lobule-scale model of bile flux using a porous medium approach (step 6 in Figure 1). A porous medium approach models bile canaliculi network topology as effective tissue porosity and permeability. We used our geometric model of the bile canaliculi network to determine the spatial porosity profile within the CV-PV axis. Similar to the bile canaliculi radius, the porosity profile revealed substantial heterogeneities within the lobule (Figure 3C, right y axis). Porosity specifically increased ~2-fold in the second cell layer next to the CV and PV (maximum 0.088 ± 0.003, mean ± SEM) compared with the middle area (minimum 0.041 ± 0.005, mean ± SEM), indicating changes of network density within the lobule. We modeled such heterogeneity using an anisotropic permeability tensor which was estimated in a spatially resolved manner (see STAR Methods section “A 3D Anisotropic Porous Medium Model of Biliary Fluid Dynamics”).

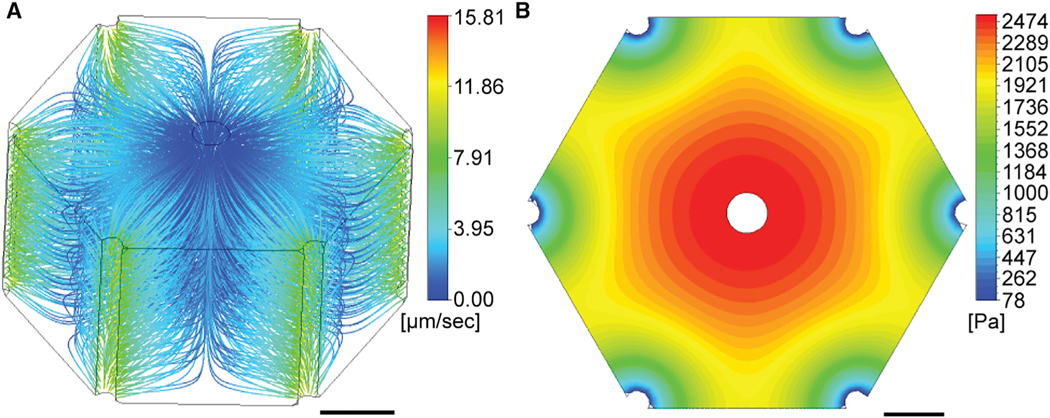
Bile velocity and pressure within the porous medium were simulated by progressive integration of the osmotic and peristaltic effects on bile flow. First, we calculated the spatial profile of the bile production rate from the predicted profile of water influx into the bile canaliculi network. To this end, we corrected our earlier model of osmotic bile secretion for the contribution of peristalsis (compare Figure S4G with Figure 4C). Second, we applied the spatial profile of the peristaltic contribution to bile velocity. Considering a bile pressure of 100 Pa at the bile ducts (Wiener et al., 2000), a CV-PV axis distance of 229 μm (Figure S2E), and impermeable interfaces between lobules, the porous medium model predicted two inversely related gradients of bile velocity and pressure within the lobule (Figures 6A and 6B). Velocity streamlines followed the kite-shaped geometry of the CV-PV axis. The bile velocity increased gradually from the CV and along the MD zone (0–3.4 μm/s) and rapidly accelerated in close proximity to the bile ducts (maximum velocity ~12 μm/s) (Figure 6A). In contrast to velocity, bile pressure decreased ~30-fold from the CV to the PV area and dropped particularly rapidly near the bile ducts (Figure 6B). The maximal bile pressure was predicted to reach 2,474 Pa (18.6 mmHg, ~20% of blood pressure) in the CV area. Such a value is consistent with the reported maximum biliary secretion pressure of 1,000–1,500 Pa in the extrahepatic biliary system in rats (Weis and Barth, 1978). Taken together, both bile velocity and pressure change by about one order of magnitude along the CV-PV axis of the liver lobule.

Figure 6. A 3D Porous Medium Model of Biliary Fluid Dynamics.

Simulation results of bile velocity (A) and bile pressure (B) from the anisotropic porous medium model. Velocity streamlines (A) and pressure profile (B) are shown in the hexagonal liver lobule geometry (CV is located in the center, PVs in the periphery). Values are color-coded as indicated by legend. Scale bars, 100 μm. See also Figure S2.

Acetaminophen Affects Biliary Fluid Dynamics at a Subtoxic Dose

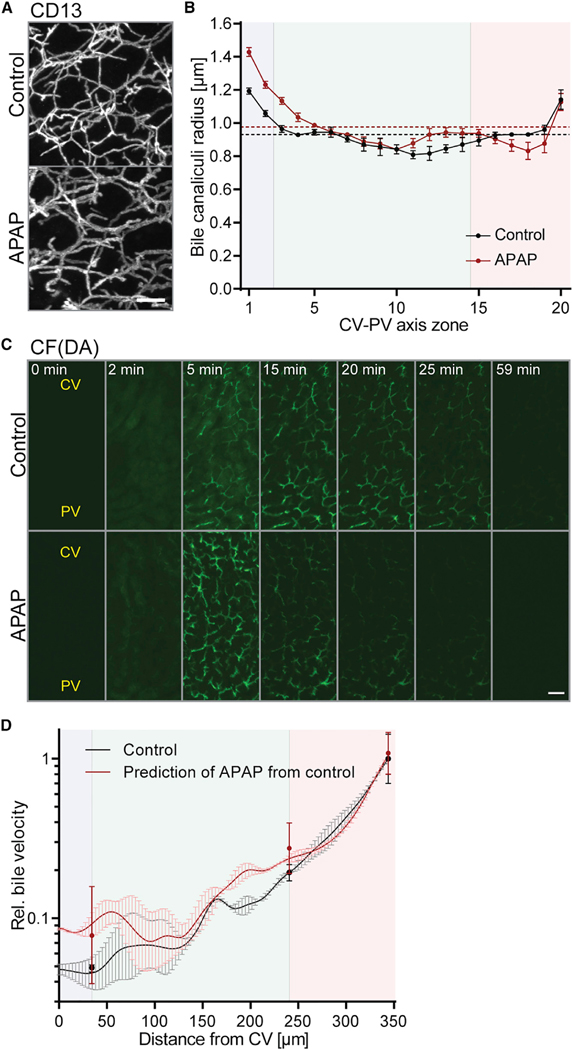
Our multi-scale model of biliary fluid dynamics is a promising tool to test and predict DILI of pharmacological compounds. Due to its clinical relevance, we chose the commonly used analgesic acetaminophen (APAP) to test it. APAP is metabolized in the liver and safe at therapeutic doses, but generates reactive metabolites upon overdose (>150 mg/kg) that can induce cholestasis from toxic hepatitis (Gillette et al., 1981; Potter and Hinson, 1987; Ruepp et al., 2002; Whitehouse et al., 1977). The reactive metabolites bind cytoplasmic proteins and, among others, cause bile canaliculi network dilation and hepatocyte necrosis (Walker et al., 1983). Using our imaging and fluid dynamics modeling pipeline, we measured the effects of APAP on biliary flow properties. To exclude side effects from hepatocyte necrosis, we chose the maximum reported subtoxic dose of APAP (150 mg/kg) and analyzed the liver tissue 2 hr after intraperitoneal (i.p.) administration. We verified that 150 mg/kg APAP did not cause significant toxic effects, such as cell death, as determined by DAPI and F-actin staining of liver tissue sections (Figure S5A). With the exception of one sample that revealed pericentral bile canaliculi network blebbing (area was excluded from the analysis), we found that APAP induced a significant dilation of bile canaliculi by up to 20% in the CV (p < 0.01) and 18% in the MD zone (p < 0.0001) (Figures 7A and 7B). Such an effect of subtoxic doses was consistent with the well-described spatial restriction of APAP toxicity to CV hepatocytes and previous reports on bile canaliculi dilation upon APAP overdose (Walker et al., 1983).

Figure 7. Acetaminophen Alters Bile Canaliculi Geometry and Bile Transport at a Subtoxic Dose.

(A) Representative IF images of fixed liver tissue sections in control or acetaminophen (APAP)-treated mice, stained for the apical marker CD13. Shown are maximum projections of ~78-μm z stacks taken in the CV area.

(B) Quantification of bile canaliculi radius (y axis) of control and APAP-treated mice in 20 equidistant zones along the CV-PV axis (x axis). Zones 1 and 20 are adjacent to the CV and PV, respectively. Average network radii are displayed as dashed lines (control, black; fasudil, red). Note: The bile canaliculi radius is smaller than in Figures 3C and 5C because tissue was immersion fixed (see STAR Methods). n = 2–3 mice, mean ± SEM. Radius of control versus APAP-treated mice, p < 0.01 (CV zone), p < 0.0001 (MD zone), p > 0.05 (PV zone).

(C) Representative images from an IVM movie of CFDA transport in control and APAP-treated mice at indicated time points after acquisition start. CFDA was injected at 1 min. Shown are maximum projections of 17-μm z-stacks. The approximate localization of the CV and PV are indicated. Movies were acquired with identical imaging settings and are displayed with the same intensity threshold values.

(D) Prediction of bile velocity in APAP-treated animals from the combined model of osmotic fluid secretion and peristalsis. The model was fit to experimental measurements of the control condition (black solid line) and the resulting velocity profile was used to predict velocity upon APAP treatment (red solid line). Velocity is expressed relative to the value of control condition at the portal end and displayed in log scale. n = 4 mice (control), n = 5 mice (APAP), mean ± 95% CI. Error bars of model results were propagated from the radius profiles shown in (B) and extrapolated across the CV-PV axis. Experimental measurements from APAP mice versus model prediction of APAP from control, p = 0.32 (CV zone), p = 0.22 (MD zone), p = 0.41 (PV zone).

The blue, green, and red backgrounds in (B) and (D) indicate the localization of the CV, MD, and PV zones, respectively. Scale bars, 10 μm (A) and 25 μm (C). See also Figure S5, Movie S4, and Tables S1 and S2.

Next, we tested our mechanistic model of osmotic fluid secretion and contractility by predicting bile flow upon APAP treatment. We first measured bile velocity by IVM of CF(DA) transport in control mice (Figures 7C and 7D; see also Figures S5B and S5C; Table S1) to calibrate our model assuming fixed relative contributions of osmotic effects and peristalsis (Figure 7D, black line). Next, we predicted bile velocity from the measured radius profile upon APAP treatment (Figure 7D, red line; see also Table S2 and STAR Methods section “Inference of Peristaltic Contribution”). The model estimated up to 2.1-fold increase in bile velocity in the CV and MD zone. Consistent with this prediction, visualization and measurement of bile velocity from IVM of CF(DA) transport revealed a specific 1.4- to 1.6-fold increase in bile velocity in the CV and MD zones, whereas the periportal zone remained almost unaffected (Figures 7C and 7D; Movie S4; see also Figures S5D and S5E). The difference between predicted and measured bile velocity upon APAP treatment was insignificant for all three zones (p ≥ 0.22). This is an independent test of the predictive power of our model of osmotic fluid secretion and peristalsis. In contrast to fasudil, the effects of APAP on osmolite secretion were marginal (Figure S5F and Table S1). Consequently, changes of apical osmolite secretion upon APAP treatment had only a minor effect on the model results (Figure S5G, compare blue and red lines). This suggested that the observed increase in bile velocity upon APAP treatment is primarily caused by the bile canaliculi network dilation in the CV and MD zones. Collectively, our results demonstrate the accuracy and applicability of our model of biliary fluid dynamics for pharmacological studies.

DISCUSSION

Bile flow is essential for the metabolic homeostasis of the liver. In this study, we established a multi-scale model of intrahepatic biliary fluid dynamics using the mouse liver as model system. A key feature of our model is the integration of realistic and accurate measurements of biliary geometry across scales and bile transport using state-of-the-art imaging technologies. Particularly, the development of image analysis algorithms was of paramount importance to quantify and simulate fluid properties in an accurate and spatially resolved manner. Based on intravital imaging of bile tracer dynamics, the model reveals structural and functional heterogeneities of biliary transport properties and establishes bile canaliculi contractility as an important determinant of bile flow in vivo. We found that bile velocity gradually increases up to ~12 μm/s from the center to the bile duct whereas biliary pressure drops by about one order of magnitude, thus revealing two opposite gradients of bile velocity and pressure within the liver lobule. Using APAP as an example, we demonstrate the precision of both the geometric model and the fluid dynamics model of the biliary system that enables the detection of phenotypes that have previously only been detected for toxic doses of APAP in liver tissue (Li et al., 2011; Walker et al., 1983). An important new finding is that osmotic pressure alone is insufficient to explain bile flow, and that bile canaliculi contractility is an additional key component. Evidence for contractility of bile canaliculi was reported about 25 years ago, yet its relevance for bile efflux has remained elusive (Watanabe et al., 1991). Our results have confirmed that bile canaliculi indeed undergo rapid directional contractile activity in vivo. Such contractility depends on the actomyosin system and its pharmacological inhibition causes a decrease in bile flux, a result that could not be predicted solely on the basis of osmotic pressure.

Cholestatic liver diseases are a heterogeneous group of disorders resulting from genetic, metabolic, and congenital defects as well as DILI (Heathcote, 2007). Although cholestasis is a prevalent cause of acute liver failure, therapeutic options are limited to urodeoxycholic acid treatment for early-stage and liver transplantation for late-stage cholestasis (European Association for the Study of the Liver, 2009). This is primarily due to the poor understanding of the underlying disease etiologies. Our model of biliary fluid dynamics provides a tool to overcome such shortcomings by enabling a mechanistic dissection of the central determinants of bile flow including bile canaliculi network geometry, hepatocyte bile transport, osmotic water influx into the bile canaliculi network, and bile canaliculi contractility. Comparative analysis of these parameters in different mouse models of cholestatic liver disease offers the opportunity to define clinical parameters for more differentiated diagnoses of cholestatic subtypes and to explore disease-specific treatment options. The imaging and image analysis approaches used in this study are based on a working pipeline that reaches medium throughput, suitable for clinical and pharmacological studies (Morales-Navarrete et al., 2015). Based on the similarity of the structural and functional properties, we expect our model established in the mouse to be translatable to human liver. Although validation of the model is technically challenging in humans, functional tests of bile acid clearance using fluorescent bile tracers, as previously tested in patients, may offer a strategy to calibrate our model to human biliary fluid dynamics (Milkiewicz et al., 2000).

STAR★METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Please contact Marino Zerial (Lead Contact, zerial@mpi-cbg.de; Max Planck Institute of Molecular Cell Biology and Genetics, Pfotenhauerstrasse 108, 01307 Dresden, Germany) for reagent and resource requests.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Mouse Work

Animal experiments performed at the National Institutes of Health (Bethesda, MD, USA) were approved by the National Institute of Dental and Craniofacial Research (NIDCR, National Institutes of Health, Bethesda, MD, USA) Animal Care and Use Committee. Animal experiments performed a the Max Planck Institute of Molecular Cell Biology and Genetics (MPI-CBG, Dresden, Germany) were conducted in accordance with German animal welfare legislation and in strict pathogen-free conditions in the animal facility of the MPI-CBG, Dresden, Germany. Protocols were approved by the Institutional Animal Welfare Officer (Tierschutzbeauftragter) and all necessary licenses were obtained from the regional Ethical Commission for Animal Experimentation of Dresden, Germany (Tierversuchskommission, Landesdirektion Dresden).

Experiments were performed on 6–10 weeks old male C57BL/6JHsd mice (Harlan laboratories) and male or female Lifeact-EGFP mice (obtained from the laboratory of R. Wedlich-Soldner (Riedl et al., 2010)). For IVM of CF(DA) transport, animals were starved for 6 h (water ad libitum) prior experiments. For imaging of bile canaliculi contractility in Lifeact-EGFP mice, animals were not starved. Fasudil and APAP were dissolved in 0.9 % saline and administered at 20 mg/kg (Fasudil) or 150 mg/kg (APAP) by i.p. injection at 1.5 h (Fasudil) or 2 h (APAP) prior imaging or organ collection. As controls, mice were administered 0.9 % saline.

METHOD DETAILS

Experimental Techniques

Protein Extraction and Western Blot

Liver tissue was lysed in ice-cold 20 mM Tris-hydrochloride (Tris-HCl) pH 7.5, 150 mM sodium hydrochloride (NaCl), 1 mM ethylenediaminetetraacetic acid (EDTA), 1 mM ethylene glycol-bis(2-aminoethylether)-tetraacetic acid (EGTA), 1 % (w/v) sodium dodecyl sulfate (SDS), 1 % (w/v) NP-40 using a pestle. Cell debris were removed by centrifugation for 10 min at 12 000 × g at 4 °C and protein was denatured at 95 °C in presence of 100 mM dithiothreitol (DTT). A total of 10 mg protein was separated by sodium dodecyl sulfate polyacrylamide gel electrophoresis, and transferred onto a nitrocellulose membrane. Membranes were blocked and incubated with primary antibodies against glyceraldehyde 3-phosphate dehydrogenase (GAPDH, 1:2000) or phospho-myosin light chain (pMLC, 1:500) and HRP-conjugated secondary antibodies (1:10000) in 5 % dry-milk, 10 mM Tris-HCl pH 8.0, 200 mM NaCl, 0.1 % Tween20. Protein was detected using the enhanced chemiluminescence (ECL) detection kit (GE Healthcare, Buckinghamshire, UK) and chemiluminescence films (GE Healthcare, Buckinghamshire, UK) according to manufacturer’s instructions.

Liver Tissue Fixation and Immunofluorescence Staining

Liver tissue of WT and Fasudil-treated animals was fixed by trans-cardial perfusion (3.7 ml/min) with 4 % paraformaldehyde (PFA), 0.1 % Tween in phosphate buffered saline (PBS) and post fixed in 4 % PFA, 0.1 % Tween, PBS (for immunofluorescence microscopy, IF) or in 2 % glutaraldehyde, PBS (for electron microscopy, EM) at 4 °C overnight. Liver tissue of APAP-treated animals and controls were only immersion fixed in 4 % PFA, 0.1 % Tween20 in PBS for 48 h at 4 °C to avoid artefacts (trans-cardial perfusion caused bile canaliculi network blebbing). For IF stainings, fixed liver tissue was mounted in 4 % low melting agarose in PBS and sectioned into 100 μm thick slices using a vibratome (Leica VT1200S). Floating sections were permeabilized in 0.5 % Triton-X100 in PBS for 1 h, quenched by incubation with 10 mM ammonium chloride (NH₄Cl) in PBS for 30 min and blocked by incubation with blocking buffer (0.2 % fish gelatin, 300 mM NaCl, 0.3 % Triton-X100 in PBS) 3 times for 5 min. Sections were incubated sequentially with a primary antibody against CD13 (1:500) in blocking buffer for 2 overnights, washed 5 times for 5 min with 0.3 % Triton-X100 in PBS, incubated with secondary antibody labelled with Alexa fluorophore 568 (1:1000), DAPI (1:2000) and Alexa fluorophore 488-conjugated Phalloidin (1:400) in blocking buffer for 2 overnights and washed again with 0.3 % Triton-X100 in PBS 5 times for 5 min. Sections were optically cleared with SeeDB (See Deep Brain) and imaged using 80 % (v/v) 2.2’-thiodiethanol as immersion medium as described previously (Ke et al., 2013). All steps were performed at room temperature.

Microscopy of Fixed Tissue

Fixed tissue was imaged with a Zeiss laser scanning microscope 780 NLO using a 63× 1.3 numerical aperture (NA) glycerol immersion objective (Zeiss), a Chameleon Ti-Sapphire 2-photon laser (780 nm), 488 and 561 laser lines and Gallium arsenide phosphide (GaAsp) detectors.

Intravital Imaging of CFDA Transport

Mouse anaesthesia was induced with 3–4 % isoflurane/ 0.3 % oxygen and maintained by i.p. injection of ketamine/xylazine throughout the experiment. Mice received 20 U of heparin dissolved in 0.9 % (w/v) NaCl by i.p. injection to prevent ischemia of the liver during the course of imaging. To visualize hepatocyte nuclei, Hoechst 33258 dissolved in 0.9 % (w/v) NaCl was administered retro-orbitally at a dose of 2 mg/kg and in a total volume of 50 μl. To expose the liver for imaging, the abdominal fur was removed using an electric shaver and a small transversal incision of 1 cm was made at the height of the sternum to expose the left lateral liver lobe using a surgical scissor and cauterizer. The mouse was positioned on the stage of an IX81 inverted confocal microscope equipped with a Fluoview 1000 scanning head (Olympus America) and a heat-adjustable UPLSAPO30X, 30× 1.05 NA silicon oil objective (Olympus). The objective was heated to 37 °C. To avoid compression of the liver lobe and to stabilize the tissue, the stage was designed with a small hole in the center into which the left lateral lobe was carefully placed. The residual volume of the hole was filled with a water-based and transparent 1 % carbomer gel (0.3 M Sorbitol, 1 % (w/v) Carbomer 940, polymerized by addition of triethanolamine and adjusted to pH 7) to immobilize the organ and prevent the organ from drying out. The bottom of the hole was designed with a cover-slide through which the organ was accessible for imaging. The animal body temperature was kept at 37 °C using a red lamp. Prior to imaging start, 18 mg/kg of 70 kDa Rhodamine-dextran or 20 ml of Qtracker 655 vascular label dissolved in 0.9 % (w/v) NaCl was injected retro-orbitally to identify the lobule orientation from the vascular flow pattern. To monitor the flux of CFDA in the liver, CFDA, dissolved in dimethyl sulfoxide (DMSO), was injected retro-orbitally at a dose of 0.2 mg/kg in a total volume of 50 μl. CFDA injection was performed slowly (approx. 30 sec) to avoid hydrodynamic effects and performed at 1 min after image acquisition start. The imaging field covered an entire CV-PV axis in the first cell layers below the liver capsule. Movies were acquired at temporal resolution of 1 min (WT, APAP and APAP control) or 2 min (Fasudil and Fasudil control) over a time course of 1 h. For each time point a 20 mm stack with an image size of 320 × 320 μm, a pixel size of 0.5–1 mm and 1 μm z-steps was acquired.

Intravital Imaging of Bile Canaliculi Contractility

For intravital imaging of bile canaliculi contractility the mouse preparation was the same as described for imaging of CFDA except of the following steps: Anaesthesia of Lifeact-EGFP mice was maintained using 3–4 % isoflurane/ 0.3 % oxygen throughout the entire experiment and imaging was performed using a Leica-DMI6000 inverted microscope with a heated stage (37 °C). Images were acquired using a 8 kHz resonant galvo-scanner and a Leica HC CS2 PL APO 63× 1.3 NA glycerol objective that was heated to 37 °C. Lifeact-EGFP was excited using a 488 laser and detected using a hybrid detector. Bile canaliculi were imaged within the first 1–2 cell layers below the liver capsule. Elastin fibres of the liver capsule were imaged by SHG microscopy using a tuneable 2-photon laser at 900 nm and a non-descanned photomultiplier tubes (PMT) detector. Movies were acquired with a pixel size of 0.09 mm and 0.020 or 0.025 sec frame rates.

Electron Microscopy

1–2 mm³ pieces of fixed liver tissue were processed for SBF-SEM pre-embedding staining, and flat embedding on glass slides in hard Durcupan resin as described previously (Deerinck et al., 2010). Small pieces of embedded tissues were cut from the slides, remounted on SBF-SEM pins using conductive glue and carbon coated. SBF-SEM was performed on a Magellan 400 SEM (Fei, The Netherlands), equipped with a Gatan 3ViewXP2 (Gatan, Munich) at 1.5 kV, 100 pA beam current, using a 12.4 nm pixel size and 40 nm-thick sections.

Mathematical and Computational Models

3D Reconstruction and Spatial Analysis of Bile Canaliculi Network Geometry

3D reconstructions of the bile canaliculi network were performed on high-resolution IF image stacks of fixed liver tissue stained for the apical marker CD13 (voxel size: 0.28 × 0.28 × 0.3 mm, 70–80 μm in depth). A tile of 2 × 1 image stacks was stitched to cover an entire CV-PV axis. Images were processed, analyzed and reconstructed using the software MotionTracking as described in (Morales-Navarrete et al., 2015). In brief, images were segmented using a local thresholding algorithm (maximum entropy), segmented objects were corrected for artefacts using standard morphological operations (opening/closing) and the triangulation mesh of the segmented surfaces was generated by the cube marching algorithm. The active mesh was tuned to align the triangle mesh vertexes to the maximum gradient of fluorescence intensity in the original image. A representation of the skeletonized image was generated using a 3D graph describing the geometrical and topological features of the bile canaliculi network. For the spatial analysis of the bile canaliculi radius, porosity and network branch density, the CV-PV axis was computationally divided into 20 equidistant zones with relative coordinate x based on the two distances of each position from the CV (d_CV) and PV (d_PV):

$$x=\frac{d_{CV}}{d_{CV}+d_{PV}}$$

Then, the average radius and porosity was determined per zone. For the radius, the minimal distance of each node of the central line of the bile canaliculi network was quantified in the xy-plane. For the bile canaliculi network branch density, the network length per tissue volume was calculated. For the tissue porosity, the bile canaliculi network was computationally divided into cubes of 20 μm³ that had a 5 μm grid spacing. For each cube, the porosity ε was calculated as the ratio of the void tissue volume of the bile canaliculi network V_V to total tissue volume V_T:

$$\epsilon =\frac{V_V}{V_T}$$

Then, the average porosity from all cubes within a zone was determined.

To determine the shortest bile canaliculi network path between the PV and CV area, bile canaliculi network end-nodes were defined based on their distance to the CV and PV. For each end-node in the CV area the shortest distance through the bile canaliculi network to an end-node in the PV area was calculated using the Dijkstra’s algorithm. From the calculated paths, the shortest one was chosen. To determine the direct CV-PV axis distance, the distance from each point of the CV to the closest one of the PV was calculated.

3D Reconstruction of a Bile Canaliculus from EM Image Stacks

SBF-SEM images were de-noised by applying a median filter and aligned using Matlab. The images were segmented by intensity thresholding and size filtering using the Imaris software and the bile canaliculi volume meshes were generated using the snappyHexMesh utility in openFoam (http://www.openfoam.org).

Correction and Quantification of IVM Movie Shift

Frames of CFDA transport movies were aligned by transitional image registration. The dextran or Hoechst channel was used as reference to align the frames of all other channels (target image) to it. The relative shift ([x,y] in 2D and [x,y,z] in 3D) of the target image stack was calculated using the phase correlation approach. The cross-correlation between stacks was computed using the Fast Fourier Transform. To determine the stability of the IVM setup, the same algorithms were applied to calculate the image shift in 2D on movies of elastin fibres.

Quantification of CF Intensities from Intravital Movies

Quantification of the CF intensity in the hepatocyte cytoplasm and bile canaliculi from IVM movies was performed using the image analysis software MotionTracking. Following correction for shift, IVM movies contained 16–21 frames per stack, covering 15–20 μm in z. To avoid liver damage from photo-toxicity, IVM movies were acquired with minimum laser intensities resulting in low signal-to-noise ratio. The resulting difference of intensity between the background and the CF fluorescence in the hepatocyte cytosol was in the range of 5–20 intensity units and varied with depth. Therefore, we used the modified Mean-Shift algorithm to separate the CF fluorescence from the background. The result of the background/foreground discrimination was checked manually (Figure S1C). The bile canaliculi were detected in three steps. First, the image was convolved with Laplacian of Gaussian. Second, pixels with an intensity > 2 standard deviations of the local noise were defined as potential bile canaliculi. The local noise was determined from the local intensity minimums in at least one of 4 discrete directions. Third, along the line of the local maximum intensity direction of a bile canaliculus, pixels that co-localized with sharp intensity transitions between the cytoplasm and sinusoids were excluded from the bile canaliculi compartment. For all compartments (cytoplasm, bile canaliculi and background), the mean intensity was calculated. To avoid mixing of compartments from light scattering of bright objects (bile canaliculi to cytoplasm and cytoplasm to background), the area within the radius of 2 pixels from the object border was excluded from the calculation.

Following segmentation, the mean intensity of the bile canaliculi and cytoplasm was corrected for the intensity of the background. Due to the low signal-to-noise ratio, the direct subtraction of background intensities from the cytosolic intensities sometimes resulted in negative values and consequently created artefacts. To avoid these artefacts, we developed a Bayesian estimation of the most probable value of the foreground intensity by considering the noise of the background and foreground intensity measurements. In short, we denoted f and b to be the foreground and background intensities which we want to estimate and m and n to be the foreground and background intensities we have measured. Then the probability of f, b given m, n is

$$p(f,b\mid m,n)=\frac{1}{Z(m,n)}p(m,n\mid f,b)p(f)p(b)$$

where p(f) and p(b) are prior distributions of the foreground and background.

We assumed that m, n are independent and normally distributed. This assumption is reasonable, because the intensities were estimated by the summation of thousands of pixels (see above) and according to the Central Limit Theorem these distributions have to converge to a normal one. Therefore:

$$p(m,n\mid f,b)=\frac{1}{2\pi {\sigma }_1{\sigma }_{2}mn}exp\left(-\frac{1}{2}\ast \left(\frac{l{n}^2\left(\frac{f+b}{m}\right)}{{\sigma }_1^2}+\frac{l{n}^2\left(\frac{b}{n}\right)}{{\sigma }_2^2}\right)\right)$$

Since we were not interested in the background value, we marginalized it:

$$p(f\mid m,n)=\frac{p(f)}{Z(m,n)}{\int }_0^{\infty }exp\left(-\frac{1}{2}\ast \left(\frac{l{n}^2\left(\frac{t+b}{m}\right)}{{\sigma }_1^2}+\frac{l{n}^2\left(\frac{b}{n}\right)}{{\sigma }_2^2}\right)\right)p(b)db$$

We assumed uniform improper prior for f and b: $p(b)=const\text{and}p(f)=const$ that resulted in:

$$p(f\mid m,n)=\frac{1}{Z(m,n)}exp-\frac{1}{2}\frac{{(m-n-f)}^2}{{\sigma }_1^2+{\sigma }_2^2})\left(1+erf\frac{(m-f){\sigma }_2^2+n{\sigma }_1^2}{\sqrt{2}\left({\sigma }_1^2+{\sigma }_2^2\right)S}\right))$$

where $S^2={\left(\frac{1}{{\sigma }_1^2}+\frac{1}{{\sigma }_2^2}\right)}^{-1}$ and Z(m,n) is normalization constant. The planes in a 3D stack were split on 16 sub-images and the values ${\sigma }_1$ and ${\sigma }_2$ were estimated from the variation of the intensity measurements between the sub-images within z-planes and across z-planes in a 3D image stack. The most probable value of f was found numerically as

$$f=\underset{f\in [0,\infty ]}{\max }\text{{}exp-\frac{1}{2}\frac{{(m-n-f)}^2}{{\sigma }_1^2+{\sigma }_2^2}\text{)}\left(1+erf\frac{(m-f){\sigma }_2^2+n{\sigma }_1^2}{\sqrt{2}\left({\sigma }_1^2+{\sigma }_2^2\right)S}\right))\}$$

Then, the resulting estimations of the compartment intensities were multiplied by their total pixel number to calculate the final integral intensity of the compartment.

Within an experimental condition (WT, controls, Fasudil or APAP-treated mice) intensities from each movie were scaled to the mean value of the condition by applying a scaling factor that was calculated as:

$$f_i=\frac{{\sum }_{j=1}^N{y}_{i,j}{y}_j}{{\sum }_{j=1}^N{y}_{i,j}^2}$$

Where $y_{i,j}$ is an intensity of i-th curve in j-th time point, $y_j$ is a mean intensity in j-th time point and $f_i$ is a scaling factor for i-th curve. For each experimental condition, the mean intensity curve was calculated from 4–5 IVM movies and later used for further mathematical modelling.

IVM movies of Lifeact-EGFP were de-noised by applying a mean filter using the Fiji software. All other IF images and movies were intensity threshold adjusted but not processed otherwise.

Mathematical 3-Compartment Model of CF(DA) Transport in the Liver

The transport of CF(DA) from the blood into and through the biliary network was described in a mathematical model that considers 3 hepatic compartments: the blood (s), hepatocyte cytoplasm (c) and bile canaliculi (b) (see Figure 2F). Dye propagation through these three compartments was modelled for three spatially distinct zones within the liver lobule: The CV, MD and PV zone as defined in Figure 2C (see also Figure S2B). The different zone geometries of the kite-shaped CV-PV axis were accounted for by introducing respective geometry factors (Figure S2C). The model considers that only a fraction of the injected CFDA is delivered to the liver, whereas the rest is cleared by other tissues at rate k_clear. The injection of CFDA into the blood circulation is described by Pulse(t). It is defined by the time point of injection start $(\tau 1)$ and the injection duration $(\tau 2)$ assuming that CFDA is injected with constant rate in time $t>\tau 1$ and $t<\tau 1+\tau 2$. Both $\tau 1\text{and}\tau 2$ were fitted by the model with boundary intervals 40–80 sec $(\tau 1)$ and 20–60 sec $(\tau 2)$. In the liver, the model considers that CFDA is taken up from the blood with a permeability coefficient Perm = 3 sec⁻¹ (according to (Breeuwer et al., 1995), considering a mammalian plasma membrane thickness of 4 nm), converted into CF by cytoplasmic esterases with cleavage rate k_cleav and secreted by apical transporters with transporter activity k_pump. To account for the spatial heterogeneity of esterase and transporter levels within the CV-PV axis, the amounts of both esterases (q_i) and apical transporters $\left(q{1}_i\right)$ were determined for each zone (i = cv, md, pv). The model further considers passive back flux of CF from the bile canaliculi into the hepatocyte cytoplasm at rate $k_{l_i}$. The bile canaliculi compartment of the three zones is connected, occurs unidirectional and sequential from the CV to the MD with transport rate $k_{t_{c{v}_{md}}}$ and form the MD to the PV zone with rate $k_{t_{{md}_{pv}}}$ and exits the network from the PV zone into the bile duct with transport rate $k_{t_{p{v}_{\mathit{\text{out}}}}}$.

The dynamics of CF(DA) were described by a set of ODEs. In the blood compartment (C_s), the flux of the tracer was described as:

$$\frac{d{C}_s}{dt}=Perm\ast Pulse(t)-k_{clear}\ast C_s$$

The flux of the tracer was described separately for the cytoplasmic compartment $\left(C_{c_i}\right)$ as:

$$\frac{d{C}_{c_{cv}}}{dt}=\frac{v_{cv}\ast k_{cleav}\ast q_{cv}}{\left(q_{cv}+C_s\right)\ast C_s}+k_{l_{cv}}\ast C_{b_{cv}}-\frac{k_{pump}\ast q{1}_{cv}}{(q{1}_{cv}+C_{c_{cv})}\ast C_{c_{cv}}}$$

$$\frac{d{C}_{c_{md}}}{dt}=\frac{v_{md}\ast k_{cleav}\ast q_{md}}{\left(q_{md}+C_s\right)\ast C_s}+k_{l_{md}}\ast C_{b_{md}}-\frac{k_{pump}\ast q{1}_{md}}{\left(q{1}_{md}+C_{c_{md}}\right)\ast C_{c_{md}}}$$

$$\frac{d{C}_{c_{pv}}}{dt}=\frac{v_{pv}\ast k_{cleav}\ast q_{pv}}{\left(q_{pv}+C_s\right)\ast C_s}+k_{l_{pv}}\ast C_{b_{pv}}-\frac{k_{pump}\ast q{1}_{pv}}{\left(q{1}_{pv}+C_{c_{pv}}\right)\ast C_{c_{pv}}}$$

And for the bile canaliculi compartment $\left(C_{bi}\right)$ as:

$$\frac{d{C}_{b_{cv}}}{dt}=\frac{k_{pump}\ast q{1}_{cv}}{\left(q{1}_{cv}+C_{c_{cv}}\right)\ast C_{c_{cv}}}-k_{l_{cv}}\ast C_{b_{cv}}-k_{t_{c{v}_{md}}}\ast C_{b_{cv}}$$

$$\frac{d{C}_{b_{md}}}{dt}=\frac{k_{pump}\ast q{1}_{md}}{\left(q{1}_{md}+C_{c_{md}}\right)\ast C_{c_{md}}}-k_{l_{md}}\ast C_{b_{md}}+k_{t_{{cv}_{md}}}\ast C_{b_{cv}}-k_{t_{{md}_{pv}}}\ast C_{b_{md}}$$

$$\frac{d{C}_{b_{pv}}}{dt}=\frac{k_{pump}\ast q{1}_{pv}}{\left(q{1}_{pv}+C_{c_{pv}}\right)\ast C_{c_{pv}}}-k_{l_{pv}}\ast C_{b_{pv}}+k_{t_{{md}_{pv}}}\ast C_{b_{md}}-k_{t_{p{v}_{\mathit{\text{out}}}}}\ast C_{b_{pv}}$$

All parameters were fitted to the experimental data by maximizing the Gaussian likelihood function using the simulation software FitModel (Zeigerer et al., 2012). Since the rate parameters could vary by orders of magnitude the logarithms of the rates were used as fitting parameters. The confidence intervals for parameters were estimated by numerical calculation of the inverse Hessian matrix of the Gaussian likelihood function (Sivia and Skilling, 2006).

Apical secretion rates ${\mathit{\text{sq}}}_i$ were calculated relative to the MD zone as follows:

$$s{q}_i=\frac{q{1}_i\ast v_{md}}{q{1}_{md}\ast v_i}$$

Bile flow velocity v_i at the interfaces of the lobule zones was estimated from the volume flux rates $k_{t_{c{v}_{md}}},k_{t_{{md}_{pv}}}\text{and}{k}_{t_{{pv}_{\mathit{\text{out}}}}}$ considering the size of the zone volumes V_i and zone boundaries $A_i(i=\text{cv},\text{md},\text{pv})$ as well as a CV-PV axis distance L of 229 μm (see Figure S2E):

$$v_{cv}=\frac{k_{t_{{cv}_{md}}}\ast V_{cv}}{A_{cv}}\ast L$$

$$v_{md}=\frac{k_{t_{{md}_{pv}}}\ast V_{md}}{A_{md}}\ast L$$

$$v_{pv}=\frac{k_{t_{p{v}_{out}}}\ast V_{pv}}{A_{pv}}\ast L$$

Computational Fluid Dynamics Simulation of Bile Flow in a 3D EM-Reconstructed Bile Canaliculus

The simulation of bile flow in a 3D reconstructed bile canaliculus from EM was carried out in the laminar regime as an incompressible and Newtonian fluid for physiologically relevant bile pressure conditions (10⁻³–10⁵ Pa) and in steady state mode using the open-source software openFoam (http://www.openfoam.org) and, specifically, the simpleFoam laminar solver therein. Grid convergence studies were conducted in the standard way in order to ascertain robustness and accuracy of the numerical simulation. To verify that bile flow inside bile canaliculi is laminar, we calculated the Reynolds number (Re) from the orders of magnitude of our measured bile velocity and bile canaliculi diameter as well as bile density and bile viscosity (Luo et al., 2007) and obtained

$$Re\sim \frac{1\frac{\mu m}{sec}\ast {10}^3\frac{kg}{m^3}\ast 1\mu m}{1mPa\ast \mathit{sec}}={10}^{-6}$$

which lies 9 orders of magnitude below the threshold to turbulent flow.

Mechanistic Model of Osmotic Fluid Secretion and Bile Flow

We developed a mechanistic model of osmotically driven secretion of biliary fluid to predict the spatial water influx profile j(x) into the bile canaliculi network and the bile flow velocity v_i at the borders of zones i = cv, md, pv along the CV-PV axis (see Figure 2C, S2B, and S2C for the definition of the zones). The model takes into account previously reported fluid mechanic properties of bile (Luo et al., 2007) and the measured geometrical parameters, including the canaliculus radius profile $a(x)=a_a(x)*r_{\mathit{\text{corr}}}$ with apparent radius $a_{\text{a}}(x)$ (e.g. shown in Figure 3C for WT mice) and correction factor r_corr = 0.344 for the hydraulic diameter or radius, a mean cumulative bile canaliculi path length L between the CV and PV of 344 μm (Figure S2D) and a linear coordinate x along a shortest path of bile canaliculi branches from a tip of the bile canaliculi network near the CV (x = 0) to a junction with a draining bile duct in the PV area (x = L), neglecting potential effects of branch points (Figure 4B). The osmotic driving due to osmolites with concentration c in the bile canaliculi lumen is considered spatially uniform (see justification below) and static (independent of the CF pulse) p_osm = RTc, causing bile canaliculi water influx j(x) to be proportional to the pressure surplus of p_osm over the local fluid pressure p(x). The local fluid pressure p(x) is monotonously decreasing from a self-organising pressure maximum at the closed central tip to zero at the open outlet, hence also j(x) is non-uniform in the general case. This feedback mechanism (Figure 4B) was modelled by a first order ODE for the fluid velocity profile v(x) at steady state according to (Mathias, 1985):

$$\frac{dv(x)}{dx}=\frac{2\kappa }{a}\left(p_{osm}-p(x)\right)$$

where κ is the water permeability of the apical membrane of hepatocytes, the factor 2/a accounts for the surface to volume ratio and v(x) is the cross-section average of the local fluid velocity. We assumed Poiseuille flow with

$$v(x)=\frac{-a^2}{8\mu }\frac{dp}{dx}$$

where μ is the fluid viscosity of bile and applied mixed boundary conditions with zero inflow v(x=0) = 0 at the closed central tip (corresponding to the Neumann boundary condition dp/dx = 0 for pressure as a(x=0) is finite) and the Dirichlet condition p(x=L) = 0 at the open outlet. The solution is

$$v(x)=v_0\sqrt{M}\frac{\mathit{sinh}(\sqrt{M}\times /L)}{\mathit{cosh}\sqrt{M}}$$

with two parameters, a velocity amplitude $V_0=\frac{a^{2}RTc}{8\mu L}$ and the dimensionless Münch number $M=\frac{16\kappa \mu L^2}{a^3}$. To factor out the measured geometrical parameters, we rewrote $V_0(x)=\frac{a{(x)}^2{p}_1}{L}$ and $M(x)=\frac{p_2{L}^2}{a{(x)}^3}$ with fit parameters p₁ and p₂. The heterogeneous radius profile $a(x)=a_a(x)*r_{corr}$ weakly modulated both terms such that the analytical solution remained a valid approximation of the heterogeneous problem. Matlab was used to fit p₁ and p₂ such that the analytical solution reproduced the measured bile flow velocity values at the border of each of the three zones (CV, MD, PV) and to determine the full spatial profile of the flow velocity v(x). The used approximation of a spatially uniform osmolite concentration profile is valid for the contributing small molecules and ions. These typically have diffusion constants of the order of D = 100 μm²/sec. Even if continuously secreted only at one location, decay with a half-life of $\tau$ = 20 min results in a steady state concentration profile with a decay length of $\sqrt{D\tau }>L$.

From the continuity equation we further calculated

$$j(x)=j_0(x)\frac{cosh(\sqrt{M(x)}x/L)}{cosh\sqrt{M(x)}}$$

with $j_0(x)=2\pi a(x)\kappa p_{\mathit{\text{osm}}}$. The resulting water influx profile was monotonously ffiincreasing (Figure 4C).

Using the equation for v₀(x) from above to replace p_osm, we could express j₀ purely as a function of the geometrical parameters of the canaliculus and the parameters v₀(x) and M(x) of the velocity solution above and obtained:

$$j_0(x)=\frac{\pi a{(x)}^2{v}_0(x)M(x)}{L}$$

Given the measured fluid velocities v_i, we could predict the complete fluid source density profile j(x) independent of the exact parameter values for membrane permeability $\kappa$, fluid viscosity μ or osmotic driving p_osm.

Inference of Osmolite Concentration Changes and Prediction of Parameter Changes

We considered the steady state balance of osmolites for the kite-shaped part of the lobule as a whole. Then the sum of sources from apical secretion,

$$J=j_{CV}+j_{MD}+j_{PV}$$

equals the sum of sinks from portal outflow

$$J=c*A_{duct}*v(x=L)$$

where A_duct is a fixed geometrical property related to the cumulative cross section area of all bile canaliculi junctions with bile ducts.

We considered the ratio of this equality for two conditions, denoted by subscripts control and treated for all quantities

$$\frac{J_t}{J_c}=\frac{c_t\ast v_t(L)}{c_c\ast v_c(L)}$$

We approximated the apical secretion fluxes of osmolites by the measured apical secretion fluxes of CF and obtained flux ratios $\frac{J_t}{J_c}$ at t = 500 sec when image segmentation had the highest accuracy due to near-maximum CF intensities in all compartments, $\frac{J_{Fasudil}}{J_{control}}=0.464$ and $\frac{J_{APAP}}{J_{control}}=0.798$. Next, we considered the ratio of the analytical solutions v(x) at x = L, that are proportional to $p_{osm}=RTc$, for each pair of conditions and calculated their ratio. From the two equations for $\frac{J_t}{J_c}\text{and}\frac{v_t(L)}{v_c(L)}$ we then eliminated the velocity ratio $\frac{V_t}{V_c}$ and obtained the osmolite concentration ratio

$$\alpha =\frac{c_t}{c_c}=\sqrt{\frac{J_t}{J_c}\ast \frac{a_c{(L)}^2\sqrt{M_c(L)}\tanh \sqrt{M_c(L)}}{a_t{(L)}^2\sqrt{M_t(L)}\tanh \sqrt{M_t(L)}}}$$

as a dimensionless number α. Note that osmolite concentration only grows with the square root of the osmolite secretion flux as a result of the negative feedback by induced water secretion and resulting osmolite washout (see Figure 4B). Therewith the alteration of parameter p₁ due to osmolite secretion changes compared to a control condition could be calculated

$$p_{1t}=\frac{{RTc}_t}{8\mu }=p_{1c}\ast \alpha$$

to then predict corresponding alterations in the velocity profile. Parameter p_2t = p_2c remained unchanged as it is independent of geometric properties and the osmolite concentration.

To demonstrate the use of directly measured geometric parameters (apparent bile canaliculi radii $a_a(x)$ for c(ontrol) and t(reated) conditions: $a_c(x),a_t(x))$ and apical secretion fluxes J_c, J_t for determining parameter values and model predictions upon a change of treatment condition, we here explicitly consider the prediction of v_t(x) upon Fasudil treatment given velocity measurements v_i for the control condition (i = cv, md, pv). First, the parameter values p_1c and p_2c for the control condition were determined by fitting the curve (just inserted the substitutions v₀ and M into the analytical model solution, see above)

$$v_c(x)=p_{1c}\sqrt{p_{2c}{\text{r}}_{corr}{a}_c(x)}\frac{\mathit{sinh}\left(\sqrt{\frac{p_{2c}}{{{\text{r}}_{corr}}^3{a}_c{(x)}^3}}x\right)}{\mathit{cosh}\sqrt{\frac{p_{2c}{L}^2}{{{\text{r}}_{corr}}^3{a}_c{(x)}^3}}}$$

to the experimental data points v_i in relative units. This yielded $p_{1c}=566.9\mathrm{\mu }{\text{m}}^{-1}\text{and}{p}_{2c}=6.656*{10}^{-6}\mathrm{\mu }\text{m}$ which were confirmed by solving the initial ODE numerically using the software Morpheus (Starruss et al., 2014). Second, the apical secretion fluxes (in arbitrary intensity units per time) at t = 500 sec from data shown in Figure S4F were summed over the entire CV-PV axis:

$$J_c=0.0041+0.0592+0.0209=0.0842\text{and}{J}_t=0.0019+0.0312+0.0059=\mathrm{0.0390.}$$

Third, using $p_{2t}=p_{2c}=6.656*{10}^{-6}\mathrm{\mu }\text{m}$ and the extrapolated bile canaliculi radii at $x=L,a_c(L)=1.320\mathrm{\mu }\text{m}$ and $a_t(L)=1.422\mathrm{\mu }\text{m}$, we calculated the osmolite concentration ratio (see above, after cancelling common factors)

$$\alpha =\sqrt{\frac{J_t}{J_c}}\ast \frac{\sqrt{a_c(L)}\tanh \sqrt{\frac{p_{2c}{L}^2}{{{\text{r}}_{corr}}^3{a}_c{(L)}^3}}}{\sqrt{a_t(L)}\tanh \sqrt{\frac{p_{2t}{L}^2}{{{\text{r}}_{corr}}^3{a}_t{(L)}^3}}}=0.6697\text{. }$$

Fourth, the final parameter $p_{1t}=p_{1c}*\alpha =379.7\mu m^{-1}$ was determined. The parameter values for all conditions are given in Table S2.

Inference of Peristaltic Contribution

We defined the contribution of peristalsis v_p(x) to bile flow velocity as the difference between the measured velocity profile v_c(x) under control conditions (where osmosis and peristalsis coexist) and the velocity profile of osmotic driving alone v_o(x) under the same condition. We obtained the velocity profile of sole osmotic driving under control conditions from the different condition of Fasudil treatment by first fitting our mechanistic model to the measured velocity profile v_f(x) upon Fasudil treatment and then calculating the corresponding velocity profile v_o(x) under control conditions by inserting the measured radius profile a_c(x) and the predicted osmolite concentration, see also Figure 5E, Table S2. The resulting function $v_p(x)=v_c(x)-v_o(x)$ is displayed as solid black curve in Figure 5F.

Next we computed the ratio $\beta (X)=\frac{V_p(x)}{V_c(x)}$ to quantify the relative local contribution of peristalsis to total bile flow velocity, shown by the dashed black curve in Figure 5F. For different experimental conditions with measured total bile flow velocity v_t(x), we could then estimate the contribution of peristalsis as $v_{tp}(x)=\beta (x)*v_t(x)$ and that of sole osmotic driving as $v_{to}(x)=(1-\beta (x))*v_t(x)$. Fitting the latter with our mechanistic model, we could predict the corresponding water influx density $j_{t_o}(x)$. We applied this workflow independently to the control of APAP treatment and the WT velocity profile. From the latter, we used the predicted fluid source profile in the 3D porous medium model.

From $V_{APAPcontro{l}_o}(X)$ we predicted $V_{APAPtreated{ }_o}(X)$ using the measured radius profile and then the peristalsis contribution by

$$v_{APAPtreate{d}_p}(x)=\frac{\beta (x)}{(1-\beta (x))}\ast v_{APAPtreate{d}_o}(x)$$

such that

$$V_{APAPtreated}(x)=V_{APAPtreated{ }_o}(x)+V_{APAPtreated{ }_p}(x)=\frac{1}{(1-\beta (x))}\ast V_{APAPtreated{ }_o}(x)$$

A 3D Anisotropic Porous Medium Model of Biliary Fluid Dynamics

The liver lobule was considered as a regular hexagonal prism, with the z-axis along its center. The top and bottom hexagonal planes were characterized by a translational periodic boundary condition. The bile canaliculi network was considered to transport bile from the center radially to the bile ducts located at the six corners of the hexagon. The network is closed at the central tips surrounding the CV (CV diameter = 90 μm), but has open outlets at the portal triad (portal triad diameter = 60 μm). Based on measurements from the 3D geometric model of the bile canaliculi network, the distance from the surface of the CV to the portal triad is 229 μm (see Figure S2E). The hexagonal edges (representing the interfaces between lobules) and the center of the lobule (surrounding the central vein) were treated as bile-impermeable solid walls. The length of the z-axis was 269 μm. The lobule was considered as porous medium with a location-dependent porosity ε(x) along the CV-PV axis as determined by our geometric measurements (Figure 3C, right y-axis). The porosity profile was described by a 10^th order polynomial fit of the experimental measurements. From the porosity profile, the location-dependent tissue permeability k(x) was estimated using the Kozeny-Carman model

$$k={\left(r*r_{corr}\right)}^2*{\epsilon }^3$$

where r is the mean bile canaliculi network radius of 1.143 μm $(r=a_a(x)$ determined from the geometric model (see also Figure 3C) and r_corr is the correction factor to account for the hydraulic diameter of bile canaliculi (see above). The spatial heterogeneity of the bile canaliculi radius does not enter here since the heterogeneous geometry of the network was already accounted for by considering an anisotropic location-dependent porosity.

For the simulation, an average bile pressure of 100 Pa was applied at the bile duct (estimated according to measurements reported in (Wiener et al., 2000)) and bile was assumed to have a viscosity of 1 mPa*sec (Luo et al., 2007). Bile flow was considered to be driven by the osmotic effects of bile secretion and peristalsis. To simulate the osmotic effect, the local bile mass production rate (in units $\frac{kg}{m^3}*sec)$ was determined. Therefore, an empirical fit of the heterogeneous fluid source profile $j_{t_o}(x)(\text{in units}\frac{\mu m^3}{\mu m}*sec)$, predicted from the combined model of osmotic fluid secretion and peristalsis, was multiplied by the spatial bile canaliculi branch density profile $\text{(in units}\frac{\mu m}{\mu m^3}$, see Figure S2F) and the bile density (928 kg/m³ (Mcintosh and Anderson, 2010)). To simulate fluid dynamics, the laminar Navier-Stokes equations at steady-state were numerically solved using the software ANSYS CFX (Ansys, Canonsburg, PA, USA). The liver lobule geometry was meshed using the ICEM CFD software (Ansys, Canonsburg, PA, USA). A mesh sensitivity study was carried out in order to define a mesh independent numerical solution. For that reason several grid configurations were used, resulting in 4.2 million tetrahedral elements. The total bile mass source in the liver lobule was estimated to be 9.784*10⁻¹¹kg/sec.

To account for the additional contribution to bile flow velocity from bile canaliculi network peristalsis, the bile velocity profile predicted by the porous medium model from the osmotic effects was multiplied by the space dependent factor $\frac{1}{1-\beta (x)}$, with $\beta (x)$ representing the inferred relative contribution of peristalsis (see above). Bile velocity and pressure were normalized to the maximum values.

QUANTIFICATION AND STATISTICAL ANALYSIS

Statistical Analysis

In all experiments, n represents the number of mice used (see Figure legends for explicit n used per experiment). Intensity measurements of CF in the bile canaliculi and hepatocyte cytoplasm from IVM movies of CFDA (Figures 2D, 2E, S4B–S4E, and S5B–S5E) are given as mean ± 68 % confidence interval (CI). The uncertainty of transport parameters from the 3-compartment model are represented as 95 % CI (Figures 2G, 4C, 5E, 7D, S5G, and Table S1). It was estimated by calculation of the inverse Hessian matrix of the Gaussian likelihood function (Sivia and Skilling, 2006). Measurements of the bile canaliculi radius, porosity and branch density from 3D reconstructions of confocal image stacks from WT, control, Fasudil-treated or APAP-treated mice (Figures 3C, S2F, 5C, and 7B) represent the mean ± SEM for each zone. The uncertainty of the inferred peristaltic contribution to the local bile velocity (Figure 5F) and the prediction of bile velocity in control or APAP-treated mice (Figures 7D and S5G) was obtained by propagation of the SEMs of the measured bile canaliculi radius profiles shown in Figures 5C and 7B, respectively. In Figures 7D and S5G, the propagated uncertainty was then extrapolated across the CV-PV axis. The significance for the difference between the model prediction of control from Fasudil vs. the experimental measure in control mice and for the difference between the model prediction of Fasudil from control vs. the experimental measure of Fasudil-treated mice (Figure 5E) was estimated using the complementary error function. The significance of the peristaltic contribution to local bile velocity in the CV vs. PV zone was estimated by Student’s t-test (Figure 5F). The significance of the differences between the radius of control and Fasudil or APAP-treated mice (Figures 5C and 7B) was estimated by Student’s t-test. The average p_value for each zone comparing the difference between experimental measurements from APAP mice vs. model prediction of APAP from control (Figure 7D) was calculated using the complementary error function.

DATA AND SOFTWARE AVAILABILITY

The software FitModel and Matlab were used to fit and predict parameters for the 3-compartment model of CFDA transport and the model of osmotic fluid secretion and peristalsis, respectively. The scripts are available as supplemental data files (Datas S1 and S2).

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Rat polyclonal antibody against CD13	Acris Antibodies	Cat#SM2298P
Rabbit polyclonal antibody against phospho-myosin light chain (pMLC)	Cell Signaling Technologies	Cat#3671
Mouse polyclonal antibody against GAPDH	Sigma-Aldrich	Cat#G8795
CF568 conjugated Donkey Anti-Rat IgG (H+L) Antibody	Biotium	Cat#20092
Alexa fluorophore 488-conjugated Phalloidin	Thermo Fisher Scientific	Cat#A12379
Peroxidase AffiniPure Goat Anti-Rabbit IgG (H+L)	Jackson Immuno Research Laboratories	Cat#111035144
Chemicals, Peptides and Recombinant Proteins
Hoechst 33258	Thermo Fisher Scientific	Cat#H3569
Tetramethylrhodamine-conjugated 2000 kDa Dextran	Thermo Fisher Scientific	Cat#D7139
Texas-Red conjugated 70 kDa Dextran	Thermo Fisher Scientific	Cat#D1830
Qtracker 655 vascular labels	Thermo Fisher Scientific	Cat#Q21021MP
Carbomer 940	Spectrum Chemical	Cat#C1477
Fasudil HCl (HA-1077)	Alfa Aesar	Cat#J60751
6-Carboxfluoreceine diacetate (CFDA)	Sigma-Aldrich	Cat#C5041
Experimental Models: Organisms/Strains
Wildtype mice	Harlan laboratories	C57BL/6JHsd mice
Lifeact-EGFP mice	Laboratory of Roland Wedlich-Soldner, University of Münster, Germany (Riedl et al., 2010)	NA
Software and Algorithms
MotionTracking	Morales-Navarrete et al., 2015	http://motiontracking.mpi-cbg.de
Imaris	BitPlane, Inc.	NA
OpenFoam	NA	http://www.openfoam.org
Fiji	Schindelin et al., 2012	https://fiji.sc
ANSYS ICEM CFD	Ansys, Inc.	NA
FitModel	Zeigerer et al., 2012	http://pluk.mpi-cbg.de/projects/fitmodel
Morpheus	Starruss et al., 2014	https://gitlab.com/morpheus.lab/morpheus
Matlab	The MathWorks, Inc.	NA
GraphPad 7	GraphPad Software, Inc.	NA

Highlights.

• The bile canaliculi network displays geometric heterogeneity within the liver lobule

• Bile flow is driven by osmotic effects and bile canaliculi contractility

• A multi-scale model reveals gradients of bile velocity and pressure within the lobule

• The multi-scale model predicts drug-induced alterations of bile flow