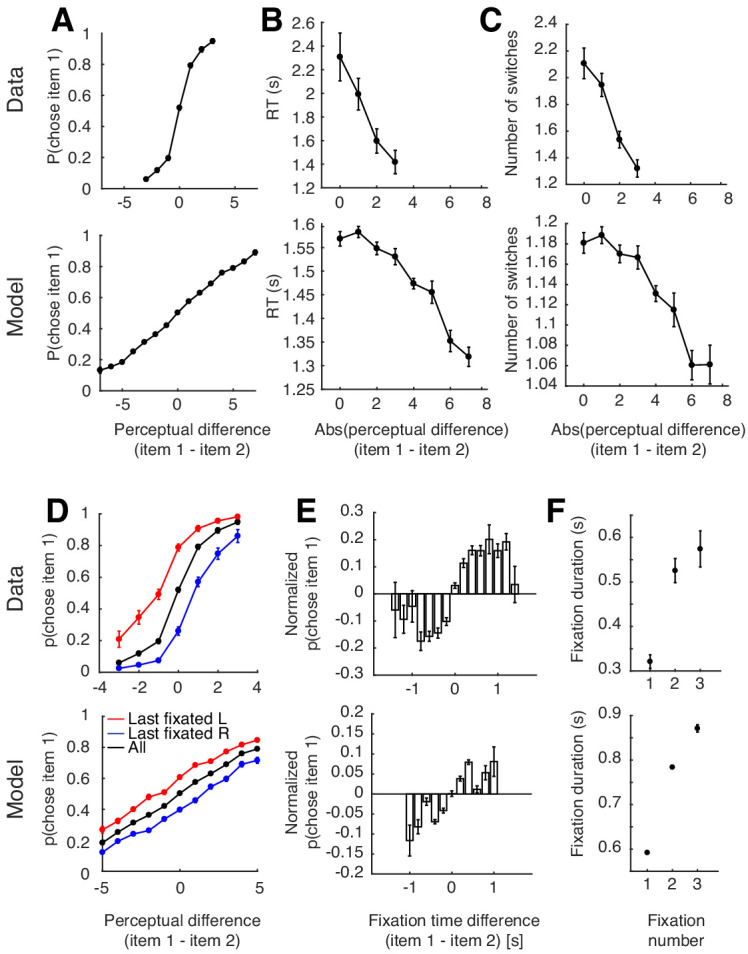
Figure 3. Replication of human behavior by simulated optimal model behavior (Krajbich et al., 2010).

(A) Monotonic increase in probability of choosing item 1 as a function of the difference in value between item 1 and 2 ($t(38)=105.7,p<0.001$). (B) Monotonic decrease in response time (RT) as a function of trial difficulty ($t(38)=-11.1,p<0.001$). RT increases with increasing difficulty. (C) Decrease in the number of attention switches as a function of trial difficulty. More switches are made for harder trials ($t(38)=-8.10,p<0.001$). (D) Effect of last fixation location on item preference. The item that was fixated on immediately prior to the decision was more likely to be chosen. (E) Attention’s biasing effect on item preference. The item was more likely to be chosen if it was attended for a longer period of time ($t(38)=5.32,p<0.001$). Since the probability of choosing item 1 depends on the degree of value difference between the two items, we normalized the p(choose item 1) by subtracting the average probability of choosing item 1 for each difference in item value. (F) Replication of fixation pattern during decision making. Both model and human data showed a fixation pattern where a short initial fixation was followed by a longer, then medium-length fixation. Error bars indicate standard error of the mean (SEM) across both human and simulated participants ($N=39$ for both). See Figure 3—figure supplement 2 for an analogous figure for the perceptual decision task.

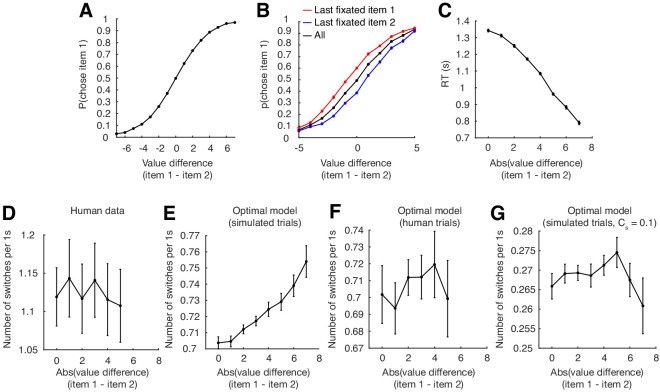
Figure 3—figure supplement 1. Parameter-dependence of psychometric/chronometric curves, and exploration of switch rate rather than switch number for the optimal model.

Parameter-dependence of psychometric/chronometric curves, and exploration of switch rate rather than switch number for the optimal model. (A–C) Psychometric (A,B) and chronometric (C) curves after decreasing the evidence noise term (${\sigma }^2$) from 27 to 5. Figure 3 suggests a qualitative difference in psychometric/chronometric curves between human and model behavior. For Figure 3A,D, the model’s psychometric curve appeared linear rather than sigmoidal. To show that this is a result of the difficulty of the task, as determined by the evidence noise term (${\sigma }^2$), and not a generalizable property of the model, we set (${\sigma }^2$) in (A) and (B) to a lower value, in which case the model exhibits sigmoidal psychometric curves. This sigmoidal shape arises because the decision becomes easier at extreme value differences and approaches perfect performance. In Figure 3B, the model’s chronometric curve had a concave shape, whereas that of the humans appeared linear. As (C) shows, decreasing the noise term diminished, but did not eliminate this concave shape. (D) Human switch rate (number of switches divided by time) did not change significantly with trial difficulty ($t(38)=-0.32,p=0.75$). (E) In the optimal model, it significantly increased with a decrease in task difficulty ($t(38)=2.96,p=0.0052$). (F) This relationship ceases to be apparent once we reduce the number of simulated trials to that of the human data ($t(38)=1.02,p=0.31$), suggesting the human data may be underpowered to show such a relationship. (G) The relationship between switch rate and trial difficulty is not a general property of the optimal model, as a significant increase in the switch cost (adjusting $C_s$ from 0.018 to 0.1) removes the effect seen in (E) ($t(38)=-0.50,p=0.62$), even with a large number of simulated trials. Error bars indicate SEM across participants.

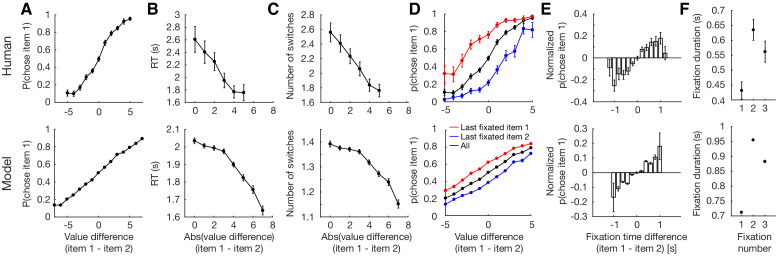
Figure 3—figure supplement 2. Replicating human perceptual decision-making behavior with the optimal model.

Replicating human perceptual decision-making behavior with the optimal model. In each trial of the perceptual decision task used in Tavares et al., 2017, human decision makers had to identify which of two presented lines were closer in orientation to a preceding target orientation. To model this decision, the authors assumed that the decision maker compares the difference in perceptual quality (i.e. angle of a line; 0°, 5°, 10°, 15°) between the target and the two lines, then converted this difference to a scale ranging from 0 to 3 with three denoting the best possible proximity (i.e. 0°). Following this, we simulated the task such that our model accumulates noisy evidence centered around the perceptual difference scale (0–3) between the target and the two lines, and chose the item with a larger value using this scale (see Appendix 1). (A) Monotonic increase in probability of choosing item 1 as a function of the perceptual difference between item 1 and 2. (B) Decrease in response time (RT) as a function of trial difficulty. (C) Decrease in the number of switches as a function of trial difficulty. (D) Effect of last fixation location on item preference. The item that was fixated on immediately prior to the decision was more likely to be chosen. (E) Attention’s biasing effect on item choice. The item was more likely to be chosen if it was attended to for a longer period of time. (F) Replication of fixation pattern during decision making. In the perceptual decision-making task, both model and human data showed increased duration for every subsequent fixation, a notable difference compared to fixation behavior in the value-based task. For (A–D), the behavioral data has a smaller range of perceptual differences due to insufficient trials with such large perceptual difference. Error bars indicate SEM across participants.