Representation of k-Mer Sets Using Spectrum-Preserving String Sets

Abstract

Given the popularity and elegance of k-mer-based tools, finding a space-efficient way to represent a set of k-mers is important for improving the scalability of bioinformatics analyses. One popular approach is to convert the set of k-mers into the more compact set of unitigs. We generalize this approach and formulate it as the problem of finding a smallest spectrum-preserving string set (SPSS) representation. We show that this problem is equivalent to finding a smallest path cover in a compacted de Bruijn graph. Using this reduction, we prove a lower bound on the size of the optimal SPSS and propose a greedy method called UST (Unitig-STitch) that results in a smaller representation than unitigs and is nearly optimal with respect to our lower bound. We demonstrate the usefulness of the SPSS formulation with two applications of UST. The first one is a compression algorithm, UST-Compress, which, we show, can store a set of k-mers by using an order-of-magnitude less disk space than other lossless compression tools. The second one is an exact static k-mer membership index, UST-FM, which, we show, improves index size by 10%–44% compared with other state-of-the-art low-memory indices.

1. Introduction

Algorithms based on k-mers are now among the top performing tools for many bioinformatics analyses. Instead of working directly with reads or alignments, these tools work with the set of k-mer substrings present in the data, often relying on specialized data structures for representing sets of k-mers (for a survey, see Chikhi et al., 2019). Since modern sequencing datasets are huge, the space used by such data structures is a bottleneck when attempting to scale up to large databases. For example, as part of our group's work on building indices for RNA-seq data, we are storing gzipped k-mer set files from about 2500 experiments (Harris and Medvedev, 2018). Though this is only a fraction of experiments in the SRA, it already consumes 6 TB of space. For these and other applications, the development of space-efficient representations of k-mer sets can improve scalability and enable novel biological discoveries.

Conway and Bromage (2011) showed that at least $log\left(\begin{array}{c}{4}^k\\ n\\ \end{array}\right)$ bits are needed to losslessly store a set of n k-mers, in the worst case. However, a set of k-mers generated from a sequencing experiment typically exhibits the spectrum-like property (Chikhi et al., 2019) and contains a lot of redundant information. Therefore, in practice, most data structures can substantially improve on that bound (Chikhi et al., 2014).

A common way to reduce the redundancy in a k-mer set K is to convert it into a set of maximal unitigs. A unitig is a non-branching path in the de Bruijn graph, a graph whose nodes are the k-mers of K and edges are the overlaps between k-mers. A unitig u can be written as a string $spell\left(u\right)$ of length $\left|u\right|+k-1$, such that the k-mers of u are exactly the k-mer substrings of $spell\left(u\right)$. For example, the unitig $\left(AAC,ACG,CGT\right)$ is spelled as AACGT. This gives a way to represent |u| k-mers using $\left|u\right|+k-1$ characters, instead of $k\left|u\right|$ characters used by a naive approach. When unitigs are long, as they are in real data, the space savings are significant. The idea can be extended to store the whole set K, because the set of maximal unitigs U forms a decomposition of K, and, therefore, has the nice property that $x\in K$ iff x is a substring of $spell\left(u\right)$, for some $u\in U$.

The maximal unitigs U can be computed efficiently (Chikhi et al., 2016; Pan et al., 2018; Guo et al., 2019) and combined with an auxiliary index to obtain a membership data structure (i.e., one that can efficiently determine whether a k-mer belongs to K or not). In particular, Unitigs-FM (Chikhi et al., 2014) and deGSM (Guo et al., 2019) use the FM-index as the auxiliary index; Pufferfish (Almodaresi et al., 2018) and BLight (Marchet et al., 2019) use a minimum perfect hash function; and Bifrost (Holley and Melsted, 2019) uses a minimizer hash table. Alternatively, U can be compressed to obtain a compressed disk representation of K, although without efficient support for membership queries before decompression.

Although unitigs conveniently fit the needs of those applications, we observe in this article that they are not necessarily the best that can be done. Concretely, we claim that what makes U useful in these scenarios is that they are a type of spectrum-preserving string set (SPSS) representation of K, which we define to be a set of strings X such that a k-mer is in K if it is a substring of a string in X. [This is in contrast to the way unitigs are used in assembly, where it is crucial that they are not chimeric (Medvedev, 2018)]. The weight of X is the number of characters it contains. In this article, we explore the idea of low-weight representations and their applicability. In particular, are there representations with a smaller weight than U that can be efficiently computed? What is the lowest weight that is achievable by a representation? Can such representations seamlessly replace unitig representations in downstream applications, and can they improve space performance?

In this article, we show that the problem of finding a minimum weight SPSS representation is equivalent to finding the smallest path cover in a compacted de Bruijn graph (Section 3). We use the reduction to give a lower bound on the weight, which could be achieved by any SPSS representation (Section 4), and we give an efficient greedy algorithm UST (Unitig-STitch) to find a representation that improves on U (Section 5) and is empirically near-optimal. We demonstrate the usefulness of our representation by using two applications (Section 6). One, we combine it with an FM-index into a membership data structure called UST-FM, and, two, we combine it with a general compression algorithm to give a compression algorithm called UST-Compress. Both applications result in a substantial space decrease over state of the art (Section 7), demonstrating the usefulness of SPSS representations. Our software is freely available at https://github.com/medvedevgroup/UST/.

1.1. Related work

The idea of using a SPSS for a membership index was previously independently described in a PhD thesis (Břinda, 2016), and questions similar to the ones in our article are simultaneously and independently studied in Břinda et al. (2020). The idea of greedily gluing unitigs (as UST does) has previously appeared in read compression (Jones et al., 2012), where contigs greedily constructed from the reads and the reads were stored as alignments to these contigs. The idea also appeared in the context of sequence assembly, where a greedy traversal of an assembly graph was used as an intermediate step during assembly (Haas et al., 2013; Kolmogorov et al., 2019).

The compression of k-mer sets has not been extensively studied, except in the context of how k-mer counters store their output (Marçais and Kingsford, 2011; Rizk et al., 2013; Kokot et al., 2017; Pandey et al., 2017c). DSK (Risk et al., 2013) uses an HDF5-based encoding, KMC3 (Kokot et al., 2017) combines a dense storage of prefixes with a sparse storage of suffixes, and Squeakr (Pandey et al., 2017c) uses a counting quotient filter (Pandey et al., 2017a). The compression of read data, on the other hand, stored in either unaligned or aligned formats, has received a lot of attention (Hosseini et al., 2016; Numanagić et al., 2016; Hernaez et al., 2019). In the scenario where the k-mer set to be compressed was originally generated from FASTA files by a k-mer counter, an alternate to k-mer compression is to compress the original FASTA file and use a k-mer counter as part of the decompression to extract the k-mers on the fly. This approach is unsatisfactory because (1) as shown in this article, it takes substantially more space than direct k-mer compression, (2) k-mer counting on the fly adds significant time and memory to the decompression process, and (3) there are applications where the k-mer set cannot be reproduced by simply counting k-mers in a FASTA file, for example, when it is a product of a multi-sample error correction algorithm (Yang et al., 2012).

Further, there are applications where the k-mer set is not related to sequence read data at all, for example, a universal hitting set (Orenstein et al., 2017), a chromosome-specific reference dictionary (Rangavittal et al., 2019), or a winnowed min-hash sketch [e.g., as in Sahlin and Medvedev (2019), or see Marçais et al. (2019) and Rowe (2019) for a survey].

Membership data structures for k-mer sets were surveyed in a recent paper (Chikhi et al., 2019). In addition to the unitig-based approaches already mentioned, other exact representations include succinct de Bruijn graphs (referred to as BOSS; Bowe et al., 2012) and their variations (Boucher et al., 2015; Blazzougui et al., 2016a), dynamic de Bruijn graphs (Belazzougui et al., 2016b; Crawford et al., 2018), and Bloom filter tries (Holley et al., 2016). Some data structures are non-static, that is, they provide the ability to insert and/or delete k-mers. However, such operations are not needed in many read-only applications, where the cost of supporting them can be avoided. Membership data structures can be extended to associate additional information with each k-mer, for instance an abundance count (e.g., deBGR; Pandey et al., 2017b) or a color class (for a short overview, see Chikhi et al., 2019).

2. Definitions

2.1. Strings

In this article, we assume all strings are over the alphabet $\Sigma =\left\{A,C,G,T\right\}$. The length of string x is denoted by $\left|x\right|$. A string of length k is called a k-mer. For a set of strings S, $weight\left(S\right)={\sum }_{x\in S}\left|x\right|$ denotes the total count of characters. We write x(i..j) to denote the substring of x from the ith to the jth character, inclusive. We define $su{f}_k\left(x\right)$ (respectively, $pr{e}_k\left(x\right)$) to be the last (respectively, first) k characters of x. For x and y with $su{f}_{k-1}\left(x\right)=pr{e}_{k-1}\left(y\right)$, we define gluing x and y as $x\odot y=x\cdot y\left[k..\left|y\right|\right]$. For $s\in \left\{0,1\right\}$, we define $orient\left(x,s\right)$ to be x if $s=0$ and to be the reverse complement of x if $s=1$. A string x is canonical if x is the lexicographically smaller of x and its reverse complement. To canonize x is to replace it by its canonical version (i.e., ${min}_i\left(orient\left(x,i\right)\right)$). We say that x₀ and x₁ have a (s₀, s₁)-oriented-overlap if $su{f}_{k-1}(orient\left(x_0,1-s_0\right)=pr{e}_{k-1}(orient\left(x_1,s_1\right))$. Intuitively, such an overlap exists between two strings if we can orient them in such a way that they are glueable. We define the k-spectrum $s{p}^k\left(x\right)$ as the multiset of all canonized k-mer substrings of x. The k-spectrum for a set of strings S is defined as $s{p}^k\left(S\right)={\bigcup }_{x\in S}s{p}^k\left(x\right)$.

2.2. Bidirected graphs

A bidirected graph G is a pair $\left(V,E\right)$ where the set V are called vertices and E is a set of edges. An edge e is a 4-tuple $\left(u_0,s_0,u_1,s_1\right)$, where $u_i\in V$ and $s_i\in \left\{0,1\right\}$, for $i\in \left\{0,1\right\}$. Intuitively, every vertex has two sides, and an edge connects to a side of a vertex. Note that there can be multiple edges between two vertices, but only one edge once the sides are fixed. An edge is a loop if $u_0=u_1$. Given a non-loop edge e that is incident to a vertex u, we denote $side\left(u,e\right)$ as the side of u to which it is incident. We say that a vertex u is isolated if it has no edge incident to it and is a dead-end if it has exactly one side to which no edges are incident. We define $n_{dead}$ and $n_{iso}$ as the number of dead-end and isolated vertices, respectively. A sequence $w=\left(u_0,e_1,u_1,\dots ,e_n,u_n\right)$ is a walk if for all $1\le i\le n$, e_i is incident to $u_{i-1}$ and to u_i, and for all $1\le i\le n-1$, $side\left(u_i,e_i\right)=1-side\left(u_i,e_{i+1}\right)$. Vertices $u_1,\dots ,u_{n-1}$ are called internal, and u₀ and u_n are called endpoints. A walk can also be a single vertex, in which case it is considered to have no internal vertex and one endpoint. A path cover W of G is a set of walks such that every vertex is in exactly one walk in W and no walk visits a vertex more than once.

2.3. Bidirected DNA graphs

A bidirected DNA graph is a bidirected graph G where every vertex u has a string label $lab\left(u\right)$, and for every edge $e=\left(u_0,s_0,u_1,s_1\right)$, there is a $\left(s_0,s_1\right)$-oriented-overlap between $lab\left(u_0\right)$ and $lab\left(u_1\right)$. G is said to be overlap-closed if there is an edge for every such overlap. Let $w=\left(u_0,e_1,u_1,\dots ,e_n,u_n\right)$ be a walk. We define $x_0=orient\left(lab\left(u_0\right),1-side\left(u_0,e_1\right)\right)$ and, for $1\le i\le n$, $x_i=orient\left(lab\left(u_i\right),side\left(u_i,e_{i-1}\right)\right)$. The spelling of a walk is defined as $spell\left(w\right)=x_0\odot \cdots \odot x_n$. (The fact that the x_i's are glueable in this way can be derived from definitions.) If W is a set of walks, then we define $spell\left(W\right)={\bigcup }_{w\in W}spell\left(w\right)$.

2.4. de Bruijn graphs

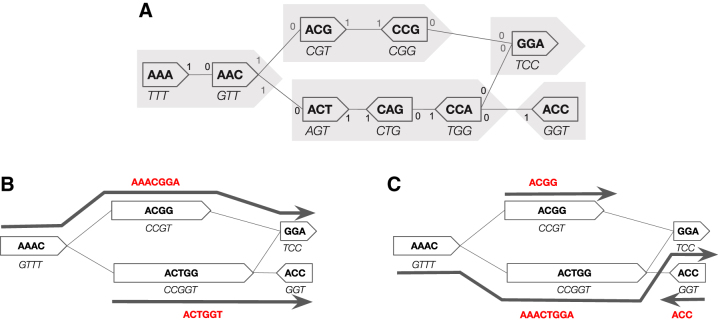
Let K be a set of canonical k-mers. The node-centric bidirected de Bruijn graph, denoted by $dBG\left(K\right)$, is the overlap-closed bidirected DNA graph where the vertices and their labels correspond to K. Figure 1A shows an example. In this article, we will assume that $dBG\left(K\right)$ is not just a single cycle; such a case is easy to handle in practice but is a space-consuming corner case in all the analyses. A walk in $dbG\left(K\right)$ is a unitig if all its vertices have in- and out-degrees of 1, except that the first vertex can have any in-degree and the last vertex can have any out-degree. A single vertex is also a unitig. A unitig is maximal if it is not a sub-walk of another unitig. It was shown in Chikhi et al. (2016) that if $dBG\left(K\right)$ is not a cycle, then a unitig cannot visit a vertex more than once, and the set of maximal unitigs forms a unique decomposition of the vertices in $dBG\left(K\right)$ into non-overlapping walks. The bidirected compacted de Bruijn graph of K, denoted by $cdBG\left(K\right)$, is the overlap-closed bidirected DNA graph where the vertices are the maximal unitigs of $dBG\left(K\right)$, and the labels of the vertices are the spellings of the unitigs. Figure 1B shows an example.

FIG. 1.

(A) An example of a de Bruijn graph for a set K with 9 3-mers. The 0 side of a vertex is drawn flat and the 1 side pointy. The text in each vertex is its label, that is, what is spelled by a walk going in the direction of the pointy end. The string below the vertex is the reverse complement of its label, which is what is spelled by a walk going in the opposite direction. The maximal unitigs are shown by filled in gray arrows. (B) The compacted de Bruijn graph for the same set K. Each vertex corresponds to a maximal unitig in the top graph. Each vertex's label corresponds to the spelling of the corresponding unitig and is shown inside the vertex; the reverse complement of the label is written below in italics. One possible path cover is five walks, each corresponding to a single vertex; the spelling of this cover is $\left\{AAAC,ACGG,ACTGG,GGA,ACC\right\}$, which is the unitig SPSS representation of K. A better path cover of size 2 that could potentially be found by our UST algorithm is shown. It corresponds to SPSS representation $\left\{AAACGGA,ACTGGT\right\}$. It is easy to verify that this path cover has minimum size, and, by Theorem 1, the corresponding representation has minimum weight (13). (C) Another path cover that could potentially be found by UST. It has size 3 and is suboptimal. SPSS, spectrum-preserving string set; UST, Unitig-STitch.

3. Equivalence of SPSS Representations and Path Covers

For this section, we fix K to be a canonical set of k-mers. A set of strings X is said to be a SPSS representation of K if their k-spectrums are equal and each string in X is of length $\ge k$. For brevity, we say X represents K. Note that because in our definitions K is a set (i.e., no duplicates) and the k-spectrum is a multi-set, this effectively restricts X to not contain duplicate k-mers (see Figure 1B, C, e.g.). In this article, we consider the problem of finding a minimum weight SPSS representation of K. In this section, we will show that it is equivalent to the problem of finding the smallest path cover of $cdBG\left(K\right)$, in the following sense:

Theorem 1. Let $X^{opt}$ be a minimum weight SPSS representation of K. Let $W^{opt}$ be the smallest path cover on $cdBG\left(K\right)$. Then, $weight(X^{opt})=\left|K\right|+|W^{opt}|\left(k-1\right)$.

First, we show that the weight of an SPSS representation is a linear increasing function of its size (i.e., the number of strings it contains) and, hence, finding an SPSS representation of minimum weight is equivalent to finding one of minimum size.

Lemma 1. Let X be an SPSS representing K. Then, $weight\left(X\right)=\left|K\right|+\left|X\right|\left(k-1\right)$.

Proof. Every string x of length $\ge k$ contains $\left|x\right|-k+1$ k-mers. X has $\left|K\right|$ k-mers, since X and K have the same k-spectrum. Combining these, $\left|K\right|={\sum }_{x\in X}\left(\left|x\right|-k+1\right)=weight\left(X\right)-\left|X\right|\left(k-1\right)$.

The intuition behind Theorem 1 is that there is a natural size-preserving bijection between path covers of $dBG\left(K\right)$ and SPSS representations of K. Since it is more efficient to work with compacted de Bruijn graphs, we would like this to hold for $cdBG\left(K\right)$ as well. However, the path covers with an endpoint at an internal vertex of a unitig in $dBG\left(K\right)$ do not project onto $cdBG\left(K\right)$. Nevertheless, this is not an issue because such path covers are necessarily non-optimal.

Lemma 2. Let W be a path cover of $cdBG\left(K\right)$. Then, $spell\left(W\right)$ represents K.

Proof. By construction, all strings in $spell\left(W\right)$ are at least k-long, so we only need to show that the spectrum of $spell\left(W\right)$ is K. Let W⁰ be the path cover with every vertex as its own walk. We can view W as being constructed from W⁰ by repeatedly taking a pair of walks that share endpoints and joining them together. We prove the Lemma by induction.

For the base case, $spell\left(W^0\right)$ are the unitigs of $dBG\left(K\right)$, which, by definition, have the same spectrum as K (Chikhi et al., 2016). Now let Wⁱ be the path cover after i walk-joins. Then, $W^{i+1}$ is the result of joining some two walks w and $w\prime$ into $w\prime \prime$. Observe that joining walks preserves the k-spectrum of their spellings, that is, $s{p}^k\left(spell\left(w\right)\right)\cup s{p}^k\left(spell\left(w\prime \right)\right)=s{p}^k\left(spell\left(w\prime \prime \right)\right)$. Combining with the inductive hypothesis for Wⁱ, $s{p}^k\left(spell\left(W^i\right)\right)=s{p}^k\left(spell\left(W^{i+1}\right)\right)$.

Lemma 3. Let X be the smallest SPSS representation of K. Then, there exists a path cover W of $cdBG\left(K\right)$ with $\left|W\right|=\left|X\right|$.

Proof. Let $X=\left\{x_1,\dots ,x_m\right\}$. Every string x_i is spelled by a walk $w{\prime }_i$ in $dBG\left(K\right)$, visiting the sequence of its canonized constituent k-mers. Since X is spectrum preserving with respect to K, it contains every k-mer in K exactly once; therefore, $\left\{w{\prime }_1,\dots ,w{\prime }_m\right\}$ is a path cover of $dbG\left(K\right)$.

Since X has the smallest number of strings, the endpoints of $w{\prime }_i$ cannot be on internal vertices of unitigs, otherwise there would exist another string x_j that could be glued with x_i to form a smaller SPSS representing K. Therefore, there exists a corresponding walk w_i in $cdBG\left(K\right)$ such that $spell\left(w_i\right)=spell\left(w{\prime }_i\right)=x_i$. Hence, the set of walks $W=\left\{w_1,\dots ,w_m\right\}$ is a path cover of $cdBG\left(K\right)$.

Now we can prove Theorem 1.

Proof. By Lemma 1, $X^{opt}$ has minimum size and, hence, by Lemma 3, there exists a path cover W with $\left|W\right|=\left|X^{opt}\right|$. By the optimality of $W^{opt}$, $\left|W^{opt}\right|\le \left|W\right|\le \left|X^{opt}\right|$. Next, by Lemma 2, $spell\left(W^{opt}\right)$ represents K and, by definition, $\left|spell\left(W^{opt}\right)\right|=\left|W^{opt}\right|$. Since $X^{opt}$ has minimum size, $\left|X^{opt}\right|\le \left|spell\left(W^{opt}\right)\right|=\left|W^{opt}\right|$. This proves $\left|X^{opt}\right|=\left|W^{opt}\right|$. Lemma 1 then implies the Theorem.

4. Lower Bound on the Weight of a SPSS Representation

In this section, we will prove a lower bound on the size of a path cover of a bidirected graph, which, by Theorem 1, gives a lower bound on the weight of any SPSS representation. Finding the minimum size of a path cover in general directed graphs is NP-hard, since a directed graph has a Hamiltonian path if and only if it has a path cover of size 1. However, we do not know the complexity of the problem when restricted to compacted de Bruijn graphs of k-mer sets. The minimum size of a path cover is known to be bounded from above by the maximum size of an independent set (at least for directed graphs; Diestel, 2005); however, finding a maximum independent set is itself NP-hard. We, therefore, take a different approach.

For this section, let $G=\left(V,E\right)$ be a bidirected graph without loops and let W be a path cover. A vertex-side is a pair $\left(u,su\right)$, where $u\in V$ and $su\in \left\{0,1\right\}$. For a non-isolated vertex u, we say $\left(u,su\right)$ is a dead-side if there are no edges incident to $\left(u,1-su\right)$. Note that the number of dead-sides is, by definition, the number of dead-end vertices. Consider a walk $\left(v_0,e_1,\dots ,e_n,v_n\right)$ with $n\ge 1$. Denote its endpoint-sides as $\left(v_0,side\left(v_0,e_1\right)\right)$ and $\left(v_n,side\left(v_n,e_n\right)\right)$. If a walk contains just one vertex $\left(v_0\right)$, then denote its endpoint-sides as $\left(v_0,0\right)$ and $\left(v_0,1\right)$.

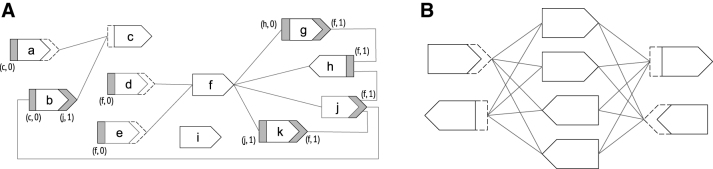
We observe that every walk in a path cover must have two unique endpoint-sides. Our strategy is to give a lower bound on the number of endpoint-sides, thereby giving a lower bound on the size of a path cover. We know, for instance, that dead-sides must be endpoint-sides and we also know that the sides of an isolated vertex must be endpoint-sides. For other cases, we cannot predict exactly the endpoint-sides, but we can create disjoint sets of vertex-sides (which we call special neighborhoods) such that, for each set, we can guarantee that all but one of its vertex-sides are endpoint-sides. Formally, for a vertex-side $\left(u,su\right)$, its special neighborhood $B_{u,su}$ is the set of vertex-sides $\left(v,sv\right)$ such that there exists an edge between $\left(u,su\right)$ and $\left(v,1-sv\right)$ and it is the only edge incident on $\left(v,1-sv\right)$. A vertex-side that belongs to a special neighborhood is called a special-side. Figure 2 shows an example. Our key lemma is that all but one member of a special neighborhood must be an endpoint-side:

FIG. 2.

(A) An example of compacted de Bruijn graph (labels not shown), with a distinct ID for each vertex shown inside the vertex. The dashed hollow sides of the vertices are dead sides, and the solid gray sides are special-sides. Each special-side is additionally labeled with the vertex-side to whose special neighborhoods it belongs. For example, the special neighborhood of vertex-side (c, 0) contains two vertex-sides, namely the blunt gray sides of vertices a and b, corresponding to $\left|B_{c,0}\right|=2$. In this example, $n_{dead}=4$, $n_{sp}=6$, and $n_{iso}=1$. By Theorem 2, the minimum size of a path cover is 6, and one can, indeed, find a path cover of this size in the graph. (B) In this example, $n_{dead}=4$, $n_{sp}=n_{iso}=0$, resulting in a lower bound of 2 on the size of a path cover. However, a quick inspection tells us that the the optimal size of a path cover is 4. This shows that our lower bound is not theoretically tight.

Lemma 4. For a vertex-side $\left(u,su\right)$, there must be at least |B_{u, su}| − 1 endpoint-sides of $W$ in $B_{u,su}$.

Proof. Assume without loss of generality that |B_u,su| > 1, since the lemma is otherwise vacuous. Let $\left(v,sv\right)\in B_{u,su}$ be a vertex-side that is not an endpoint-side in W, and let w_v be the walk containing v. Since, in particular, $\left(v,sv\right)$ is not an endpoint-side of w_v, then w_v must contain an edge incident to $\left(v,1-sv\right)$. By definition of special neighborhood, the only such edge is incident to $\left(u,su\right)$. By definition of a path cover, there can only be one walk in W that contains an edge incident to $\left(u,su\right)$ and it can contain only one such edge. Hence, there can only be one $\left(v,sv\right)\in B_{u,su}$ that is not an endpoint-side.

Next, we show that the special neighborhoods are disjoint, and we can therefore define $n_{sp}={\sum }_{u\in V,su\in \left\{0,1\right\}}max\left(0,\left|B_{u,su}\right|-1\right)$ as a lower bound on the number of special-sides that are endpoint-sides:

Lemma 5. There are at least $n_{sp}$ special-sides that are endpoint-sides of W.

Proof. We claim that $B_{u,su}\cap B_{v,sv}=\varnothing$ for all $\left(u,su\right)\ne \left(v,su\right)$. Let $\left(w,sw\right)\in B_{u,su}\cap B_{v,sv}$. By definition of B_u,su, the only edge touching $\left(w,1-sw\right)$ is incident to $\left(u,su\right)$. Similarly, by definition of B_v, the only edge touching $\left(w,1-sw\right)$ is incident to $\left(v,sv\right)$. Hence, $\left(u,su\right)=\left(v,sv\right)$. The Lemma follows by applying Lemma 4 to each $B_{u,su}$ and summing the result.

Finally, we are ready to prove our lower bound on the size of path cover.

Theorem 2. $\left|W\right|\ge \lceil \left(n_{dead}+n_{sp}\right)∕2\rceil +n_{iso}$.

Proof. Define a walk as isolated if it has only one vertex and that vertex is isolated. There are exactly $n_{iso}$ isolated walks in W. Next, dead-sides are trivially endpoint-sides of a non-isolated walk in W by Lemma 5, and so are at least $n_{sp}$ of the special-sides. Since the set of dead-sides and the set of special-sides are, by their definition, disjoint, the number of distinct endpoint-sides of non-isolated walks is at least $n_{dead}+n_{sp}$. Since every walk in a path cover must have exactly two distinct endpoint-sides, there must be at least $\lceil \left(n_{dead}+n_{sp}\right)∕2\rceil$ non-isolated walks.

By applying Theorem 1 to Theorem 2 and observing that loops do not affect path covers, we get a lower bound on the minimum weight of any SPSS representation:

Corollary 1. Let K be a set of canonical k-mers and let $X^{opt}$ be its minimum weight SPSS representation. Then, $weight(X^{opt}{)}^3\left|K\right|+\left(k-1\right)\left(é(n_{dead}+n_{sp})∕2ù+n_{iso}\right)$, where $n_{dead}$, $n_{iso}$, and $n_{sp}$ are defined with respect to the graph obtained by removing loops from $cdBG\left(K\right)$.

We note that the lower bound is not tight, as in the example of Figure 2B; it can likely be improved by accounting for higher-order relationships in G. However, the empirical gap between our lower bound and algorithm is so small (Section 7) that we did not pursue this direction.

5. The UST Algorithm for Computing a SPSS Representation

In this section, we describe our algorithm called UST for computing an SPSS representation of a set of k-mers K. We first use the Bcalm2 tool (Chikhi et al., 2016) to construct $cdBG\left(K\right)$, then find a path cover W of $cdBG\left(K\right)$, and finally output $spell\left(W\right)$, which by Lemma 2 is an SPSS representation of K.

The UST constructs a path cover W by greedily exploring the vertices, with each vertex explored exactly once. We maintain the invariant that W is a path cover over all the vertices explored up to that point, and that the currently explored vertex is an endpoint of a walk in W. To start, we pick an arbitrary vertex u, add a walk consisting of only u to W, and start an exploration from u.

An exploration from u works as follows. First, we mark u as explored. Let w_u be the walk in W that contains u as an endpoint, and let su be the endpoint-side of u in w_u. We then search for an edge $e=\left(u,1-su,v,sv\right)$, for some v and sv. If we find such an edge and v has not been explored, then we extend w_u with e and start a new exploration from v. If v has been explored and is an endpoint vertex of a walk w_v in W, then we merge w_u and w_v together if the orientations allow (i.e., if $1-sv$ is the side at which w_v is incident to v) and start a new exploration from an arbitrary unexplored vertex. In all other cases (i.e., if e is not found, if the orientations do not allow merging w_v with w_u, or if v in internal vertex in w_v), we start a new exploration from an arbitrary unexplored vertex. The algorithm is terminated once all the vertices have been explored. It follows directly via the loop invariant that the algorithm finds a path cover, though we omit an explicit proof.

In our implementation, we do not store the walks W explicitly but rather just store a walk ID at every vertex along with some associated information. This makes the algorithm run-time and memory linear in the number of vertices and the number of edges, except for the possibility of needing to merge walks (i.e., merging of w_u and w_v). But we implement these operations by using a union-find data structure, making the total time near-linear.

We note that the UST's path cover depends on the arbitrary choices of which vertex to explore. Figure 1C gives an example of where this leads to suboptimal results. However, our results indicate that UST cannot be significantly improved in practice, at least for the datasets we consider (Section 7).

6. Applications

We apply the UST to solve two problems. First, we use it to construct a compression algorithm UST-Compress. UST-Compress supports only compression and decompression and not membership and is intended to reduce disk space. We take K as input [in the binary output format of either DSK (Risk et al., 2013) or Jellyfish (Marçais and Kingsford, 2011)], run UST on K, and finally compress the resulting SPSS by using a generic nucleotide compressor MFC (Pinho and Prats, 2013). UST-Compress can also be run in a mode that takes as input a count associated with each k-mer. In this mode, it outputs a list of counts in the order of their respective k-mers in the output SPSS representation (this is a trivial modification to UST). This list is then compressed by using the generic LZMA compression algorithm. Note that we use MFC and LZMA due to their superior compression ratios, but other compressors could be substituted. To decompress, we simply run the MFC or LZMA decompressing algorithm.

Second, we use UST to construct an exact static membership data structure UST-FM. Given K, we first run UST on K, and then construct an FM-index (Ferragina and Manzine, 2000) (as implemented in https://github.com/jts/dbgfm) on top of the resulting SPSS representation. The FM-index then supports membership queries. In comparison to hash-based approaches, the FM-index does not support insertion or deletion; on the other hand, it allows membership queries of strings shorter than k.

7. Empirical Results

We use different types of publicly available sequencing data, because each type may result in a de Bruijn graph with different properties and may inherently be more or less compressible. Our datasets include human, bacterial, and fish samples; they also include genomic, metagenomic, and RNA-seq data (Table 1). Each dataset was k-mer counted by using DSK (Risk et al., 2013), using $k=31$ with singleton k-mers removed. Although these are not the optimal values for each of the respective applications, it allows us to have a uniform comparison across datasets. In addition, we k-mer count one of the datasets with $k=61$, removing singletons, to study the effect of k-mer size. All our experiments were run on a server with an Intel^® Xeon^® CPU E5-2683 v4 @ 2.10 GHz with 64 cores and 512 GB of memory. All tested algorithms were verified for correctness in all datasets. Table 2 shows the version numbers of all tools tested, and further reproducibility details are available at https://github.com/medvedevgroup/UST/tree/master/experiments.

Table 1.

Dataset Characteristics

Dataset	Source	No. of reads	Read length (bp)	No. of distinct k-mers
Zebrafish RNA-seq	SRX3022435	59,741,039	101	124,740,993
Human RNA-seq	SRR957915	49,459,840	101	101,017,526
Human chromosome 14	GAGE (Salzberg et al., 2012)	36,504,800	101	99,941,572
Whole human genome	SRR034939	36,201,642	100	391,766,120
Human gut metagenome	SRR341725	25,479,128	90	103,814,001
Human RNA-seq ($k=61$)	SRR957915	49,459,840	101	75,013,109

Singletons are not included in the k-mer count. Unless otherwise stated, $k=31$.

Table 2.

Versions of the Tools Used in Experiments

Tool	URL	Git commit hash/version	Non-default option
Bcalm2	https://github.com/gatb/bcalm	f4e0012e8056c56a04c7b00a927c260d5dbd2636	-kmer-size 31 -abundance-min 2 -all-abundance-counts
Cosmo/VARI	https://github.com/cosmo-team/cosmo/tree/VARI	d35bc3dd2d6ba7861232c49274dc6c63320cedc1	-d
Dbgfm	https://github.com/jts/dbgfm	ef82d38af2c402beab9ef9f12a72e7dcaeff210c
KMC	https://github.com/refresh-bio/KMC	85ad76956d890aa24fc8525eee5653078ed86ace	-fa -k31 -ci2 -sm -m2
Squeakr	https://github.com/splatlab/squeakr	aa30936a40ac07b556d48b867ccadcebc5525021	-e -k 31 -c 2 -s 2000 -t 1
McCortex	https://github.com/mcveanlab/mccortex/	d3901d900cacff376e1201e86223adf1cc56784a
MFC	http://bioinformatics.ua.pt/software/mfcompress/	Version 1.01

Default options were used except as noted in the last column. We show the options for $k=31$. Reproducibility details are available at https://github.com/medvedevgroup/UST/tree/master/experiments.

7.1. Evaluation of the UST representation

We compare our UST representation against the unitig representation as well as against the SPSS lower bound of Corollary 1 (Table 3, with a deeper breakdown in Table 4). The UST reduces the number of nucleotides (i.e., weight) compared to the unitigs by 10%–32%, depending on the dataset. The number of nucleotides obtained is always within 3% of the SPSS lower bound; in fact, when considering the gap between the unitig representation and the lower bound, UST closes 92%–99% of that gap. These results indicate that our greedy algorithm is a nearly optimal SPSS representation, on these datasets. They also indicate that the lower bound of Corollary 1, though not theoretically tight, is nearly tight on the type of real data captured by our experiments.

Table 3.

Comparison of Different String Set Representations and the SPSS Lower Bound

Dataset	No. of distinct k-mers	SPSS lower bound		UST		unitigs
		No. of strings	nt/k-mer	No. of strings	nt/k-mer	No. of strings	nt/k-mer
Zebrafish RNA-seq	124,740,993	3,979,856	1.96	4,174,867	2.00	7,775,719	2.87
Human RNA-seq	101,017,526	3,924,803	2.17	4,132,115	2.23	7,665,682	3.28
Human chromosome 14	99,941,572	2,235,267	1.67	2,386,324	1.72	4,871,245	2.46
Whole human genome	391,766,120	13,964,825	2.07	14,423,449	2.10	19,581,835	2.50
Human gut metagenome	103,814,001	1,517,107	1.34	1,522,139	1.34	2,187,669	1.49
Human RNA-seq (k = 61)	75,013,109	2,651,729	3.12	2,713,825	3.17	4,371,173	4.50

The second column shows $\left|K\right|$. For a representation X, the number of strings is $\left|X\right|$ and the number of nucleotides per distinct k-mer is $weight\left(X\right)|K|$. Unitigs were computed by using BCALM2.

SPSS, spectrum-preserving string set; UST, Unitig-STitch.

Table 4.

Percent of $cdBG\left(K\right)$ Vertex-Sides That Belong to Isolated Vertices, That Are Dead-Sides, and That Are Counted by $n_{sp}$

Dataset	$2n_{iso}$	$n_{dead}$	$n_{sp}$
Zebrafish RNA-seq	13	18	21
Human RNA-seq	13	20	18
Human chromosome 14	10	14	21
Whole human genome	54	8	9
Human gut metagenome	44	10	15
Human RNA-seq ($k=61$)	24	22	15

7.2. Evaluation of UST-compress

We measure the compressed space usage (Table 5), compression time and memory (Table 6), and decompression time and memory. We compare against the following lossless compression strategies: (1) the binary output of the k-mer counters DSK (Risk et al., 2013), KMC (Kokot et al., 2017), and Squeakr-exact (Pandey et al., 2017c); (2) the original FASTA sequences, with headers removed; (3) the maximal unitigs; and (4) the BOSS representation (Bowe et al., 2012) (as implemented in COSMO [https://github.com/cosmo-team/cosmo/tree/VARI]). In all cases, the stored data are additionally compressed by using MFC (for nucleotide sequences, i.e., 2 and 3) or LZMA (for binary data, i.e., 1 and 4). The second strategy (which we already discussed in Section 1.1) is not a k-mer compression strategy per say, but it is how many users store their data in practice. The fourth strategy uses BOSS, the empirically most space efficient exact membership data structure according to a recent comparison (Crawford et al., 2018). We include this comparison to measure the advantage that can be gained by not needing to support membership queries. Note that strategies 1 and 2 retain count information, unlike strategies 3 and 4. Squeakr-exact also has an option to store only the k-mers, without counts.

Table 5.

Space Usage of UST-Compress and Others

Dataset	With counts					Without counts
	Squeakr	KMC	DSK	FASTA	UST-compress	Squeakr	BOSS	Unitigs	UST-compress
Zebrafish RNA-seq	91	41	47	33	5.4	45	5.9	5.0	3.6
Human RNA-seq	94	41	48	41	6.3	41	6.9	5.8	4.1
Human chromosome 14	98	43	48	49	5.8	41	5.5	4.3	3.1
Whole human genome	85	41	43	17	4.7	40	7.0	4.7	4.1
Human gut metagenome	90	46	51	23	4.2	44	5.3	3.0	2.7
Human RNA-seq (k = 61)	—	82	77	41	6.4	—	9.0	5.5	4.3

We show the average number of bits per distinct k-mer in the dataset. All files are compressed with MFC or LZMA, in addition to the tool shown in the column name. Squeakr-exact's implementation is limited to $k<32$ (Pandey et al., 2017c) and so it could not be run for $k=61$.

Table 6.

Time and Peak Memory Usage of UST-Compress (Without Counts) and Others During Compression

Dataset	Time (minutes)									Peak memory (GB)
	BOSS			Unitigs			UST-compress			BOSS	Unitigs	UST-compress
	Cosmo	LZMA	Total	bcalm2	MFC	Total	UST	MFC	Total
Zebrafish RNA-seq	6.3	0.7	7.0	3.0	1.5	4.4	1.5	0.9	5.3	4.0	3.1	3.1
Human RNA-seq	4.0	0.8	4.8	4.7	1.3	5.9	1.6	0.8	7.1	3.6	3.4	3.4
Human chromosome 14	4.9	0.5	5.4	2.1	1.0	3.1	1.1	0.7	3.9	4.2	3.4	3.4
Whole human genome	17.3	3.0	20.3	10.4	2.2	12.5	4.1	1.9	16.3	4.0	4.3	4.3
Human gut metagenome	6.6	0.7	7.3	3.2	0.9	4.0	0.5	0.8	4.5	3.3	3.9	3.9
Human RNA-seq (k = 61)	4.4	0.6	5.0	3.6	3.9	7.5	1.1	2.4	7.1	4.3	2.3	2.3

For BOSS and unitigs, the times are separated according to the two steps of compression: running the core algorithm (Cosmo and bcalm2) followed by the generic compressor (respectively, LZMA and MFC). For UST-Compress, the first step is exactly the same as for unitigs (Bcalm2), so the column is not repeated.

First, we observe that compared with the compressed native output of k-mer counters, UST-Compress reduces the space by roughly an order of magnitude; this, however, comes at an expense of compression time. When the value of k is increased, this improvement becomes even higher; as k nearly doubles, the UST-Compress output size remains the same; however, the compressed binary files output by k-mer counters approximately double in size. Our results indicate that when disk space is a more limited resource than compute time, SPSS-based compression can be very beneficial.

Second, we observe a 4–8 × space improvement compared with just compressing the reads FASTA file. In this case, however, the extra time needed for UST compression is balanced by the extra time needed to recount the k-mers from the FASTA file. Therefore, if all that is used downstream are the k-mers and possibly their counts, then SPSS-based compression is again very beneficial. Third, UST-Compress uses between 39% and 48% less space than BOSS, with comparable construction time and memory. Fourth, compared with the other SPSS-based compression (based on maximal unitigs), UST-Compress uses 10% to 29% less space, but it has 10% to 24% slower compression times (with the exception of the $k=61$ dataset, where it compresses 6% faster). The ratio of space savings after compression closely parallels the ratio of the weights of the two SPSS representations (Table 3). Fifth, we note that the best compression ratios achieved are significantly better than the worst case Conway Bromage lower bound of $>35$ bits per k-mer for the $k=31$ datasets and 95 bits per k-mer for the $k=61$ dataset. Finally, we note that the differences in the peak construction memory, and the total decompression run time and memory ($<2$ minutes and $<1$ GB for UST-Compress, respectively, table not shown) were negligible.

We also compressed a subset of samples from a de-noised index of 450,000 microbial DNA data used recently in large-scale indexing projects of BIGSI (Bradley et al., 2019) and COBS (Bingmann et al., 2019). Each sample consists of error-corrected 31-mers (without abundance information) from a corresponding sequencing experiment, natively stored as bzipped McCortex binary file [see Bingmann et al. (2019) and Bradley et al. (2019) for details]. We downloaded 19,000 of these files from http://ftp.ebi.ac.uk/pub/software/bigsi/nat_biotech_2018/ctx/. We ran UST-Compress, which reduced the disk space from 507 to 14.7 GB, a 35 × reduction. The compression took a total of 82 hours and a peak memory of 3 GB (using one core).

7.3. Evaluation of UST-FM

We measure the memory taken by the data structure (Table 8), the query times (Table 9), and the time and memory taken during construction (Table 7). We compare UST-FM against two other space-efficient exact static membership data structures for k-mer sets. The first builds the FM index on top of the maximal unitigs (we refer to this as unitig-FM, but it is referred to originally as dbgfm in Chikhi et al., 2014). The second is BOSS, which, as previously mentioned, was shown (Crawford et al., 2018) to have superior space usage. We did not compare against the Bloom filter trie (Holley et al., 2016), which is fast but uses an order of magnitude more memory than BOSS (Crawford et al., 2018). Other data structures, such as Pufferfish (Almodaresi et al., 2018), blight (Marchet et al., 2019), and Bifrost (Holley and Melsted, 2019), implement more sophisticated operations and hence use significantly more memory than BOSS. Moreover, these make use of a unitig SPSS representation and hence could potentially themselves incorporate the UST approach.

Table 8.

UST-FM Data Structure Size, Shown in the Average Number of Bits per Distinct k-Mer in the Dataset

Dataset	BOSS	Unitigs-FM	UST-FM
Zebrafish RNA-seq	7.5	7.9	5.5
Human RNA-seq	9.0	9.2	6.3
Human chromosome 14	8.7	6.9	4.8
Whole human genome	7.7	6.8	5.7
Human gut metagenome	8.8	5.4	4.9
Human RNA-seq (k = 61)	13.4	13.6	10.0

This was measured by taking the peak memory usage during membership queries.

Table 9.

UST-FM Query Time (in Seconds) for Two Sets of 10,000 k-Mers Each, Using the Human RNA-Seq Indices

	BOSS	Unitigs-FM	UST-FM
$k=31$
$x\in K$	3.80	0.51	0.49
$x\notin K$	1.48	0.38	0.37
$k=61$
$x\in K$	15.25	1.61	1.58
$x\notin K$	5.10	0.35	0.37

The first set contains k-mers drawn from the dataset, so that UST-FM returns a hit. The second set takes randomly generated k-mers that were verified to not be present in the dataset. We measured the query times (per k-mer) after the index was already loaded into memory.

Table 7.

Time and Memory for Construction of Index by UST-FM and Others

Dataset	Time (minutes)			Memory (GB)
	BOSS	Unitigs-FM	UST-FM	BOSS	Unitigs-FM	UST-FM
Zebrafish RNA-seq	6.3	24	17	4.0	3.1	3.1
Human RNA-seq	4.0	21	15	3.6	3.4	3.4
Human chromosome 14	4.9	15	11	4.2	3.4	3.4
Whole human genome	17.3	111	92	4.0	4.3	4.3
Human gut metagenome	6.6	13	12	3.3	3.9	3.9
Human RNA-seq (k = 61)	4.2	16	9	4.3	2.3	2.3

First, the UST-FM index is 25%–44% smaller and the queries are 4 to 11 times faster compared with BOSS; however, it takes 2 to 5 times longer to build. This time is dominated by FM-index construction, rather than by UST. Second, the UST-FM index is 10%–32% smaller than the unitigs-FM index, with a negligibly faster query time. Finally, the memory use during construction was similar for all approaches.

8. Conclusion

In this article, we define the notion of an SPSS representation of a set of k-mers, give a lower bound on what could be achieved by such a representation, and give an algorithm to compute a representation that comes close to the lower bound. We demonstrate the applicability of the SPSS definition by using our algorithm to substantially improve space efficiency of the state of the art in two applications.

A natural question is why we limit ourselves to SPSS representations. One can imagine alternative strategies, such as allowing a k-mer to appear more than once in the string set, or allowing other types of characters. In fact, for any concrete application, one might argue that an SPSS representation is too restrictive and can be improved. However, we chose to focus on SPSS representations because they are the common denominator in the applications of unitig-based representations we have observed (Chikhi et al., 2014; Almodaresi et al., 2018; Holley and Melsted, 2019; Marchet et al., 2019). In this way, they retain broad applicability, as opposed to more specialized representations.

One limitation of the UST is the time and memory needed to run Bcalm2 as a first step. Bcalm2 works by repeatedly gluing k-mers into longer strings, taking care to never glue across a unitig boundary. However, this care is wasted in our case, since the UST then greedily glues across unitig boundaries anyway. Therefore, a potentially significant speedup and memory reduction of UST would be to implement it as a modification of Bcalm2, as opposed to running on top of it. This can keep the high-level algorithm the same but change the implementation to work directly on the k-mer set by incorporating algorithmic aspects of Bcalm2.

Author Disclosure Statement

The authors declare they have no competing financial interests.

Funding Information

P.M. and A.R. were supported by NSF awards 1453527 and 1439057. A.R. is supported by NIH Computation, Bioinformatics, and Statistics training program.