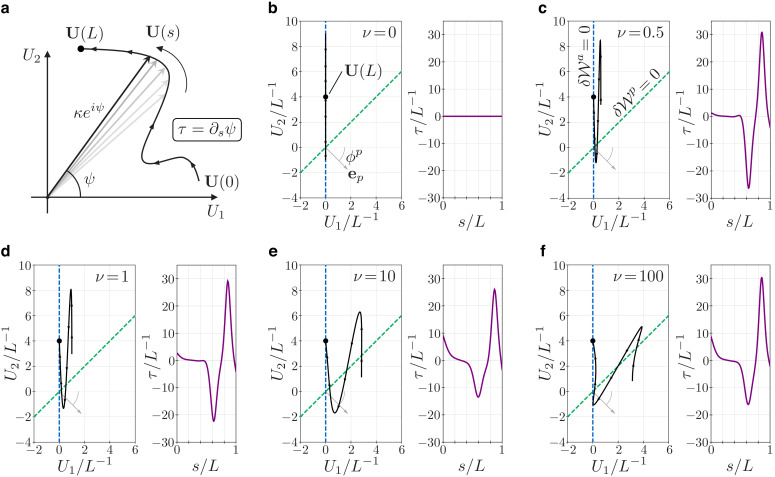
Figure 6. Geometry and mechanics of non-planar flagellar shapes.

(a) The bending vector $\mathbf{𝐔}(s)=(U_1(s),U_2(s))$ traces a curve on the plane of the bending parameters ${\displaystyle U_1}$ and ${\displaystyle U_2}$. The norm of the bending vector determines the curvature $\kappa (s)=|\mathbf{𝐔}(s)|$ of the flagellum. The rate of change of the angle $\psi (s)$ determines the torsion $\tau ={\partial }_s\psi$. (b–f) Bending vectors’ traces of flagellar equilibrium configurations under the same (steady) dynein actuation, but different values of the material parameter $\nu =D^p/(B^a{L}^{-2})$. Equilibria are minimizer of the energy $𝒲={𝒲}^a+{𝒲}^p$. For small values of ${\displaystyle \nu }$, the Ax component of the energy ${𝒲}^a$ dominates. In this case, $\mathbf{𝐔}$ is close to the target bending vector $(0,U_2^{*})$ where $U_2^{*}(s)=A_0+A_1\sin (2\pi s/L)$. For large values of ${\displaystyle \nu }$ the PFR component of the energy ${𝒲}^p$ dominates, and equilibria are dragged closer to the line orthogonal to the vector ${\mathbf{𝐞}}_p$ (dashed green). The bending vector undergoes rotations which result in torsional peaks of alternating sign.