Fig. 3. Quantum optical analysis of CR—for measuring the emitter’s wave function.

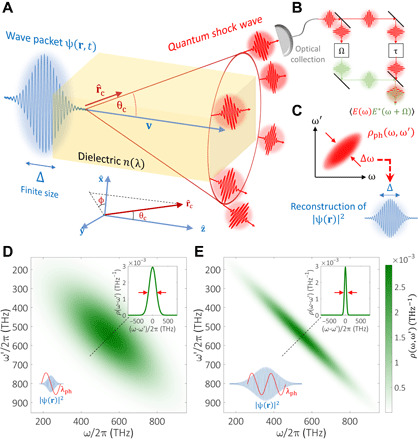
(A) A charged particle wave packet ψ(r, t) of finite size Δ and carrier velocity v₀ impinges on a Cherenkov detector with material dispersion n(ω). The particle spontaneously emits quantum shock waves of light into a cone with opening half-angle θ_c(ω) = acos[1/βn(ω)]. Collection optics is situated along the cone in the direction ${\widehat{\mathbf{r}}}_{\mathrm{c}}$ in the far field. (B) Detection scheme for measuring the spectral field autocorrelations ⟨E(ω)E(ω′)⟩ using an interference between spectrally/temporally sheared fields (57). (C) The reconstructed photon density matrix determines the spatial probability distribution ∣ψ(r)∣². (D and E) Simulation of particle wave function size reconstruction from the photon density matrix. A single 1-MeV electron (β = 0.94) in a silica Cherenkov detector [dispersion taken from (77)] emits CR that is collected within the visible range (λ = 400 to 700 nm, centered at λ₀ = 550 nm). The electron wave function envelope is Gaussian and spherically symmetric, with position uncertainty of (d) Δx_e = 254 nm and (E) Δx_e = 1016 nm (bottom insets). In both (D) and (E), the measured photon density matrix, ρ_ph(ω, ω′), is plotted. The wave function–independent diagonal ρ_ph(ω, ω) that denotes the photodetection probability is the same for both cases. However, the off-diagonal spectral coherence ρ_ph(ω − ω′) is strongly dependent on the wave function. Measuring its width Δω_coh (top insets) and using the approximate Eq. 7 provide the estimates (D) $\mathrm{\Delta }{\tilde{x}}_{\mathrm{e}}=290 \text{nm}$ and (E) $\mathrm{\Delta }{\tilde{x}}_{\mathrm{e}}=1006 \text{nm}$.