Yellow fever virus outbreak in Brazil under current and future climate

Abstract

Introduction

Yellow fever (YF) is primarily transmitted by Haemagogus species of mosquitoes. Under climate change, mosquitoes and the pathogens that they carry are expected to develop faster, potentially impacting the case count and duration of YF outbreaks. The aim of this study was to determine how YF virus outbreaks in Brazil may change under future climate, using ensemble simulations from regional climate models under RCP4.5 and RCP8.5 scenarios for three time periods: 2011–2040 (short-term), 2041–2070 (mid-term), and 2071–2100 (long-term).

Methods

A compartmental model was developed to fit the 2017/18 YF outbreak data in Brazil using least squares optimization. To explore the impact of climate change, temperature-sensitive mosquito parameters were set to change over projected time periods using polynomial equations fitted to their relationship with temperature according to the average temperature for years 2011–2040, 2041–2070, and 2071–2100 for climate change scenarios using RCP4.5 and RCP8.5, where RCP4.5/RCP8.5 corresponds to intermediate/high radiative forcing values and to moderate/higher warming trends. A sensitivity analysis was conducted to determine how the temperature-sensitive parameters impacted model results, and to determine how vaccination could play a role in reducing YF in Brazil.

Results

Yellow fever case projections for Brazil from the models varied when climate change scenarios were applied, including the peak clinical case incidence, cumulative clinical case incidence, time to peak incidence, and the outbreak duration. Overall, a decrease in YF cases and outbreak duration was observed. Comparing the observed incidence in 2017/18 to the projected incidence in 2070–2100, for RCP4.5, the cumulative case incidence decreased from 184 to 161, and the outbreak duration decreased from 21 to 20 weeks. For RCP8.5, the peak case incidence decreased from 184 to 147, and the outbreak duration decreased from 21 to 17 weeks. The observed decrease was primarily due to temperature increasing beyond that suitable for Haemagogus mosquito survival.

Conclusions

Climate change is anticipated to have an impact on mosquito-borne diseases. We found outbreaks of YF may reduce in intensity as temperatures increase in Brazil; however, temperature is not the only factor involved with disease transmission. Other factors must be explored to determine the attributable impact of climate change on mosquito-borne diseases.

Introduction

Yellow fever (YF) virus is a Flavivirus similar to dengue and Zika virus and is endemic to South America and Africa. In South America, it is transmitted by Haemagogus janthinomys and Haemagogus leucocelaenus species of mosquitoes in jungle environments, and occasionally by Aedes aegypti and Aedes albopictus in urban environments (de Abreu et al., 2019). In general, YF virus transmission occurs in sylvatic cycles where mosquitoes feed on, and transmit, YF virus between non-human primates; however, humans living in or travelling along the border between forested and peri-urban or in rural areas can easily be infected when bitten by infectious mosquitoes. Yellow fever virus can also be transmitted in an urban environment; however, this has not been documented in Brazil since the 1940s (Bryant et al., 2007; Chippaux & Chippaux, 2018). Symptoms of YF include fever, headache, muscle pain, nausea, vomiting, and fatigue (Monath & Vasconcelos, 2015). The virus attacks the liver, causing jaundice, hence the name of the disease. Approximately 55% of individuals with YF virus are asymptomatic, 26% have mild symptoms, while 19% experience severe symptoms that can lead to death (Johansson et al., 2014; Monath, 2001). An effective, safe and affordable vaccine is available, and a single dose is sufficient to provide immunity for life. Immunity is reached within ten days for 80–100% of vaccinated individuals and within 30 days for 99% of vaccinated individuals (Monath & Vasconcelos, 2015). There are currently no specific antiviral medications for YF.

In South America, YF virus is generally endemic in the Amazon, and parts of Peru, Colombia, Venezuela, Guyana, Surinam, French Guiana, and Brazil (Chippaux & Chippaux, 2018; Ministry of Health, 2018; Nishino et al., 2016). While the last urban YF epidemic occurred in the 1930s in Brazil, there has been a recent re-emergence of sylvatic YF that has the potential to transmit to urban locations (Chippaux & Chippaux, 2018; Ministry of Health, 2018; Nishino et al., 2016). The reason for the re-emergence of YF virus in Brazil is not fully understood. The re-emergence may be due to increasing deforestation, which increases the contact between the canopy-dwelling Haemagogus spp. and humans, travel and migration between endemic and epidemic regions, and low immunization coverage in some areas that were previously not considered at-risk for YF (Chaves et al., 2018, Chen et al., 2019; Chippaux & Chippaux, 2018; Dyer, 2017; Ortiz-Martinez et al., 2017).

In Brazil, YF outbreaks generally occur between November and April, during the rainy season (Ministry of Health, 2018). The average monthly temperature in 2018 ranges from 22 °C to 26 °C. These temperatures are typical in Brazil, as the historical monthly average temperatures from 1971 to 2000 also range from 22 °C to 26 °C (Giorgi et al., 2009). During the 2017/18 season, there were 1257 confirmed cases and 394 deaths (Ministry of Health, 2018). The majority of cases were in rural areas. The outbreak was declared by the Ministry of Health in Brazil, and we defined an outbreak as an increase in the number of cases over the normal yearly case numbers (Portia et al., 2014).

Climate change is a change in global or regional climate patterns, primarily attributed to the increased atmospheric carbon dioxide produced by the use of fossil fuels (Nema et al., 2012). The future climate is projected using representative concentration pathways (RCPs), which are defined by their total cumulative measure of human-produced greenhouse gas emissions by 2100 (van Vuuren, Edmonds, Kainuma, Riahi, Thomson, et al., 2011). There are four RCP pathways: RCP2.6, which includes a strict mitigation scenario and the least emissions; RCP4.5 and RCP6.0, which are moderate scenarios, and represent a 2 °C temperature increase globally; and RCP8.5, which is the worst-case scenario, includes high emissions, and represents a 4 °C increase in global annual mean temperature (IPCC, 2014; van Vuuren et al., 2011).

In Brazil, climate change may cause an overall increase in temperature (Nema et al., 2012). New regions in Brazil may be hospitable to mosquitoes with the changing climate, such as in more temperate regions (Lowe et al., 2018). In contrast, other regions, such as parts of the Amazon, may become inhospitable to the vectors (Lowe et al., 2018). Temperature has an impact on mosquito birth and death rate, as well as the extrinsic incubation period (EIP); the time between a mosquito acquiring a virus and being able to transmit it (Ciota & Keyel, 2019; Kamal et al., 2018; Wu, Peak, et al., 2016). For Haemagogus spp., under increasing temperatures, the development rate is expected to increase as the mosquito moves through its life stages faster; the death rate is expected to decrease until 25 °C, the temperature threshold at which the death rate of mosquitoes begins to increase; and the EIP is expected to decrease as the replication rate of the virus in the mosquito increases (Lee et al., 2016; Marinho et al., 2016; Suparit et al., 2018; Tesla et al., 2018). These relationships between temperature and mosquito ecology may change mosquito distributions throughout Brazil and impact the pathogens’ transmission rate between humans and mosquitoes (Kamal et al., 2018). In Brazil, high rainfall and a temperature increase of 2 °C within the last decade were followed by an increased number of YF cases in non-human primates, and then human cases (Almeida et al., 2014; de Thoisy et al., 2020). With the anticipated increase in cases with increasing temperature, it is expected that an increase in imported cases will also be observed. Cases of YF have already been imported to other countries from South America, such as the Netherlands and Canada (Hamer et al., 2018; PHAC, 2016). To date, there have been 15 imported cases reported in Canada (PHAC, 2020). The number of imported cases was likely much higher due to asymptomatic cases and reporting bias. There were no known imported cases reported in Canada during the South American 2017/18 outbreak (PHAC, 2020).

Many models have investigated YF virus transmission in humans (Raimundo et al., 2015; J. T., 2016; Wu, Peak, et al., 2016; Yusuf & Daniel, 2019; Zhao et al., 2018) and the importation of YF from South America to other countries (Brent et al., 2018; Dorigatti et al., 2017; Johansson et al., 2012; Sakamoto et al., 2018). A research gap exists in modelling YF virus transmission under climate change scenarios. It is expected that the number of cases will continue to rise in Brazil due to climate change, as seen in other modelling studies in other subtropical locations (Ryan et al., 2018; Tesla et al., 2018; Wu, Peak, et al., 2016). The extent of the anticipated change has not been quantified in Brazil to date.

The objective of this study was to develop a mathematical compartmental model for YF virus transmission in humans and to investigate how YF virus outbreaks in Brazil may change under future climate from regional climate model simulations, using RCP4.5 and RCP8.5 scenarios for three time periods 2011–2040 (short-term), 2041–2070 (mid-term), and 2071–2100 (long-term).

Materials and methods

Model format

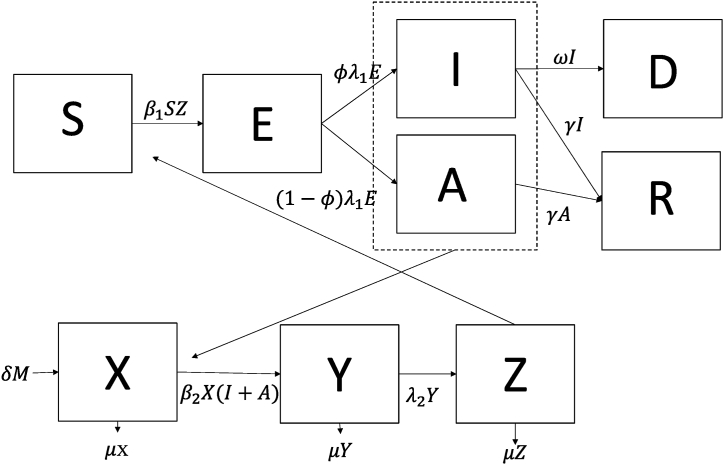
We simulated the 2017/2018 YF virus outbreak in Brazil by modifying a compartment model describing chikungunya dynamics created by Yakob and Clements (Yakob & Clements, 2013), as YF virus and chikungunya virus are both spread by mosquitoes, have latent periods and asymptomatic carriers of the virus (Fig. 1). The 2017/18 YF virus outbreak was used to the determine a baseline scenario and estimate the model outputs of an outbreak similar to the one in 2017/18 in future climate scenarios. Further information on the model format and equations can be found in appendix (A.1).

Fig. 1.

Model structure representing the compartments, where S are susceptible humans, E are exposed humans, I are symptomatic infectious humans, A are asymptomatic infectious humans, R are recovered humans, D are the human deaths due to YF, X are susceptible mosquitoes, Y are exposed mosquitoes, and Z are infectious mosquitoes. The virus is transmitted from mosquitoes to humans with a probability of β₁ when infectious mosquitoes take a blood feed from susceptible humans, and the virus is transmitted from humans to mosquitoes with a probability of β₂ when susceptible mosquitoes take a blood meal from infectious humans (asymptomatic and symptomatic, as denoted by the dotted line). Parameters are described in Table 1.

We made four simplifying assumptions: first, the human population was closed (i.e., no births or natural deaths were included in the model). The mosquito population was open, as we assumed that the mosquitoes would die while they are infectious due to their short lifespan (maximum 20 days; Bates, 1947). Second, we assumed that there was a homogeneously mixed population, where all humans and mosquitoes in Brazil were equally likely to acquire and transmit YF virus. Third, we assumed that transmission was occurring between humans and mosquitoes and did not include non-human primates as intermediate hosts. We modelled Haemagogus spp. as the mosquito vector of interest, as they were the vectors implicated in the Brazil outbreak (deAbreau et al., 2019). Fourth, we assumed that the intrinsic incubation period and recovery rate were the same for both symptomatic and asymptomatic individuals. The model was developed in R (R Core Team, 2019, Vienna, Austria).

Optimization

We used least squares optimization to estimate the transmission parameters from mosquitoes to humans and from humans to mosquitoes, the initial number of susceptible mosquitoes, and the initial number of exposed mosquitoes. We conducted the optimization by fitting the human symptomatic infectious compartment to the 2017/2018 YF virus case count data in Brazil (Ministry of Health, 2018). The case count data were extracted from the Brazilian Ministry of Health epidemic curve using ImageJ (Rasband, W.S., ImageJ, U. S. National Institutes of Health, Bethesda, Maryland, USA, https://imagej.nih.gov/ij/, 1997–2018). To capture the heterogeneity in the parameters used to model YF outbreaks, parameters were drawn from a set of probability distributions according to the literature (Table 1). The parameter distributions were identified using maximum likelihood estimation, as implemented by the fitdistplus package in R (Delignette-Muller & Dutang, 2015). To determine the best fit parameters, we found the global minimum by running ten thousand iterations using the box-constraint Broyden-Fletcher-Goldfarb-Shanno (L-BFGS-B) algorithm. The algorithm finds the global minimum by using a gradient projection method of optimization with a set of constraints for each iteration (Byrd et al., 1995). The optimization was conducted using R’s optim function (R Core Team, 2019, Vienna, Austria).

Table 1.

Parameter values in the YF model including best fit parameters for the 2017/18 YF virus outbreak in Brazil (Ministry of Health, 2018). The value of the parameter was chosen from the associated distribution. The distributions were used to introduce heterogeneity into the model parameters when conducting the least squares optimization.

Symbol	Name	Description	Value per week (distribution)	Source
${\beta }_1$	Transmission rate (mosquito to human)	Rate at which mosquitos infect humans	5.22e-7 infections per week	Fit to the 2017/18 YF virus outbreak in Brazil (Ministry of Health, 2018)
${\beta }_2$	Transmission rate (human to mosquito)	Rate at which humans infect mosquitos	1e-12 infections per week	Fit to the 2017/18 YF virus outbreak in Brazil (Ministry of Health, 2018)
$\phi$	Proportion of symptomatic humans	Proportion of infected individuals who develop symptoms	0.45	Johansson et al. (2014)
$\omega$	Death rate (humans)	Average of the rate of death per week of symptomatic humans during the 2016/17 and 2017/18 YF outbreaks	2.38 human deaths per week	World Health Organization (2019)
$1/{\lambda }_1$	Incubation period (human)	Rate of symptom onset after initial infection per week (human)	1.31 per human week Gamma (1.17,2.33)	(Johansson et al., 2010; Monath, 2001)
$1/{\lambda }_2$	Extrinsic incubation period (mosquito)	Rate of viraemic onset after initial infection per week (mosquito)	0.54 per mosquito week Gamma (0.5,0.7)	(Bates & Roca-Garcia, 1946; Johansson et al., 2010; Monath, 2001)
$1/\gamma$	Duration of infectiousness	Rate of viraemia completion after infection (symptomatic and asymptomatic humans)	0.82 per mosquito week Pert (0.63,0.85)	(Johansson et al., 2012; Massad et al., 2001)
$\mu$	Death rate (mosquito)	Rate at which mosquitoes die per week	0.36 per mosquito week Pert (0.35,1.4)	Bates (1947)
$\delta$	Development rate (mosquito)	Rate at which mosquitoes develop from hatching to adult per week	0.58 per mosquito week Pert (0.5,0.7)	(Alencar et al., 2008; Bates, 1947; Degallier et al., 2006; Tátila-Ferreira et al., 2017)

Current and future Climate scenarios

Climate data for the period when the 2017/2018 outbreak occurred was not necessary as the climatic conditions under which it occurred are inherent in the data and thus assumed to represent the current climate period. For future climate scenarios, we obtained South American monthly minimum and maximum temperature (°Celsius) data from an ensemble of regional climate models (RCMs). These data were obtained from the COordinated Regional Downscaling EXperiment (CORDEX; Giorgi et al., 2009) datasets for the South America Domain with a horizontal resolution of 0.44° (SAM-44; CORDEX-SAM44, n.d.). An ensemble climate model was created for the monthly minimum and maximum temperatures (°Celsius) for each RCP4.5 and RCP8.5 scenario (van Vuuren et al., 2011) for years 2011–2100 using ten individual models’ combinations (A.2). We chose to use RCP4.5 and RCP8.5 as they represent a middle- and worst-case climate change scenario by 2100 (van Vuuren et al., 2011). We used these RCPs for consistency and greater sample size, due to the limited number of simulations available for other RCPs. We used two R packages, R raster (Hijmans, 2019) and maptools (Bivand & Lewin-Koh, 2019), to extract the temperature data for Brazil. We obtained the monthly mean temperature by averaging the minimum and maximum temperatures for both RCP scenarios using a moving five-year average, and then averaged these values across years for each month from 2011 to 2040, 2041–2070, and 2071–2100; these time periods represent short-, medium-, and long-term projected climate change scenarios.

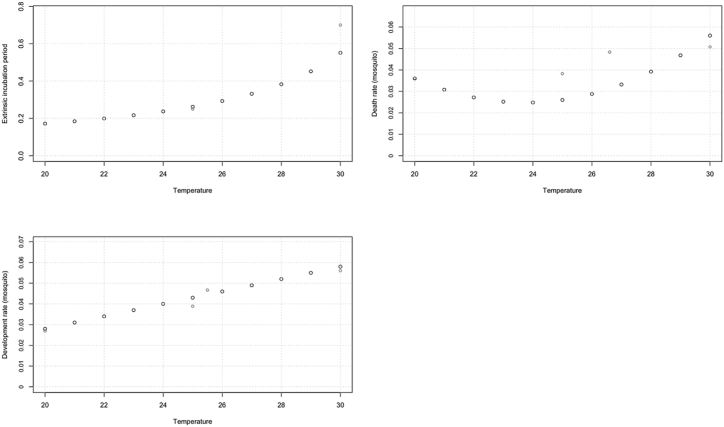
We developed polynomial equations for each of the three temperature-dependent mosquito parameters (EIP, death rate, and development rate) using laboratory data (Table 3 and Fig. 2). The best-fit polynomial equations were chosen based on an analysis of variance (ANOVA) test, where the best-fit polynomial was chosen on a significance level of 0.05. The equations were then used with the best parameter estimates for the model from the 2017/2018 YF virus outbreak to estimate the number of symptomatic infectious individuals over time for both RCP4.5 and RCP8.5 for each time period. It was assumed that the outbreak was being introduced into a population where 80% of the population was immune in each time period, due to a combination of both natural immunity and vaccination (Machado et al., 2013; Shearer et al., 2017).

Table 3.

Polynomial equations to describe the parameters’ relationship to temperature (°C).

Parameter	Polynomial Equation	Source
Extrinsic incubation period	1/(96.69–2.8 T)∗7	Bates and Roca-Garcia (1946)
Death rate (mosquito)	4.76–0.38 T + 0.008T2	Bates (1947)
Development rate (mosquito)	−0.32 + 0.03 T	Bates (1947)

Fig. 2.

Plots showing the relationship of the three climate-dependent parameters (EIP, death rate, and development rate) with temperature (°C). The red circles indicate the original laboratory data points for EIP (Bates & Roca-Garcia, 1946), and the mosquito death and development rates (Bates, 1947).

Sensitivity analysis

A sensitivity analysis was conducted to examine how sensitive the model outcomes (the peak incidence, number of weeks to the peak, and the duration of the outbreak) were to temperature changes related to the temperature-dependent parameters (mosquito death and development rates and the EIP), and to determine whether a parameter was more or less sensitive to climate. The analysis was conducted by determining the value of the parameters using polynomial equations (Table 3) associated with the parameters with a 1 °C difference. The temperatures used were 25 °C and 26 °C, as 25 °C is the temperature at which the death rate of mosquitoes begins to increase. The model was, then, run with the new parameter values one-by-one for each new parameter value (a total of six times), while keeping the other parameters the same as the base model.

An additional analysis was conducted to explore the impact of vaccination and herd immunity on YF transmission by reducing the proportion of the susceptible human population from 10% to 90% in 10%-increments. The model was run with the parameters used for the base model for each proportion.

Results

Fitted model using 2017/18 outbreak data

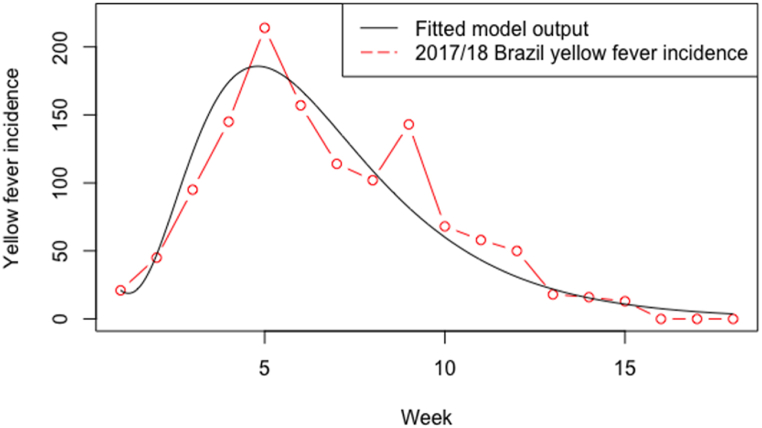
Model results showed a good fit between the symptomatic infectious individuals and observed incidence (Fig. 3). The model underestimated the peak incidence by 30 cases, the cumulative incidence by 4 cases, and number of weeks to peak by 1 week, but overestimated the duration of the outbreak by 6 weeks (Table 4). All best fit parameters and variables are shown in Table 1, Table 2 respectively.

Fig. 3.

Number of modelled clinical human cases (black line) by week compared to the observed incidence of the 2017/18 YF virus outbreak in Brazil, from December to April (red dots and dashed line).

Table 4.

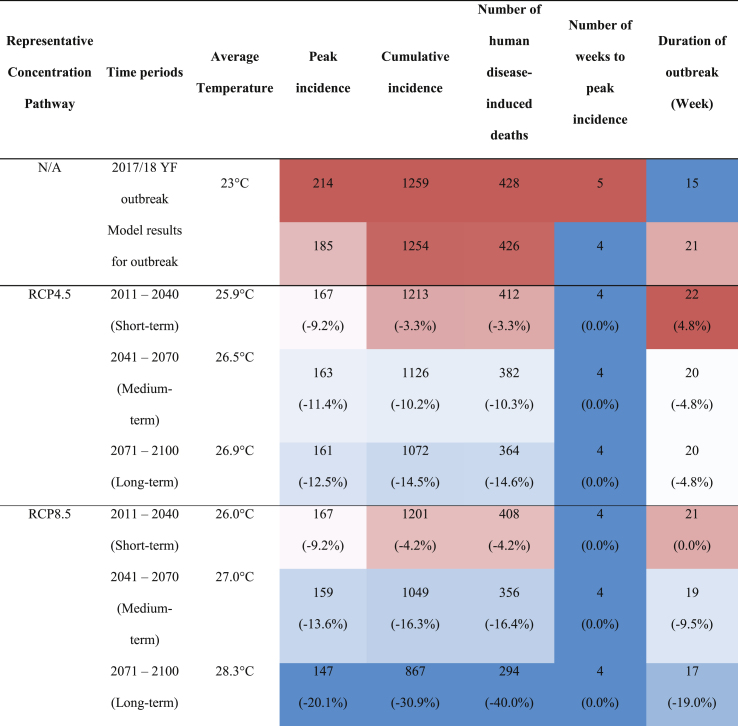
Model results fitted to the current outbreak and under future climates (RCP4.5 and RCP8.5) for short-, medium-, and long-term time periods. Each column is presented from blue (lowest value) to white (medium) to red (highest value). The percentages below the values represent the difference between the observed and predicted values. For reference, the estimated projected population of Brazil averaged across the short-, medium-, and long-term time periods are 221,537,000, 230,769,000, and 22-,976,000 respectively (United Nations Population Division, 2019).

Table 2.

Best fit initial conditions used in the YF model, fitted to the 2017/18 YF virus outbreak in Brazil (Ministry of Health, 2018).

Symbol	Name	Value	Source
N	Total human population	209,469,000	United Nations Population Division (2019)
S	Susceptible humans	41,893,754	Total human population minus remaining human compartments (N – E − I – A – R) Approximately 20% of the population is estimated to be susceptible.
E	Exposed humans	0	Estimated
I	Infectious humans (symptomatic)	21	First day of case count
A	Infectious humans (asymptomatic)	25	Estimated from proportion of symptomatic humans
R	Recovered	0.8∗N	Estimated, where about 50–60% of the overall population show immunization records (Shearer et al., 2017) and 97% of a rural Brazilian population show titres to YF virus (Machado et al., 2013)
D	Total human deaths due to YF	0	Estimated
M	Total mosquito population	418,938,000	Estimated double human population (Fitzgibbon et al., 2017; Wang et al., 2017)
X	Susceptible mosquitoes	418,937,761	Total mosquito population minus remaining mosquito components (M – Y – Z)
Y	Exposed mosquitoes	150	Fitted to the 2017/18 YF virus outbreak in Brazil (Ministry of Health, 2018)
Z	Infectious mosquitoes	995	Fitted to the 2017/18 YF virus outbreak in Brazil (Ministry of Health, 2018)

Climate change projection models

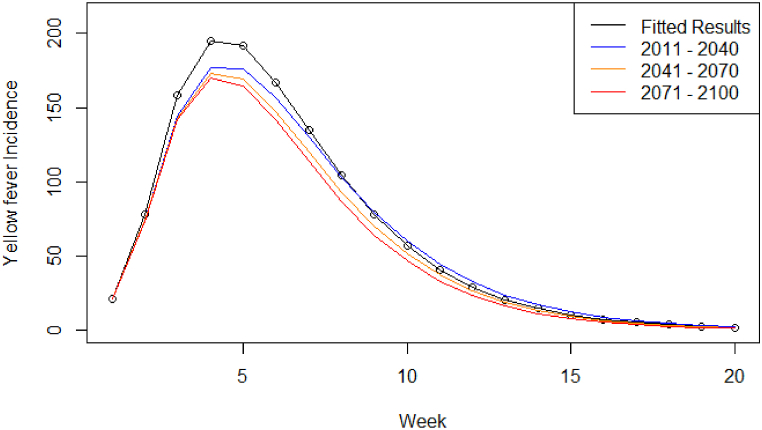
The number of cases at peak for both RCP scenarios decreased compared to the 2017/18 outbreak numbers. For RCP4.5 (Fig. 4) there was a 1.1-fold decrease between the modelled results and the short-term time period (18 cases at peak), a 1.02-fold decrease between short- and medium-term (4 cases at peak), and a 1.01-fold decrease between medium- and long-term (2 cases at peak), indicating a decreasing trend as the temperature increases (Table 4). A similar pattern was also observed for the cumulative case counts and estimated number of deaths. The number of weeks to the peak number of symptomatic cases remained the same, while the duration of the outbreak decreased as the temperature increased (from 22 to 20 weeks) (Table 4).

Fig. 4.

Symptomatic infectious humans (Compartment I) model output for scenario RCP4.5, from 2011 to 2040 (blue), 2041–2070 (orange), and 2071–2100 (red), compared to the model output fitted to the 2017/18 YF virus outbreak (black circles and line).

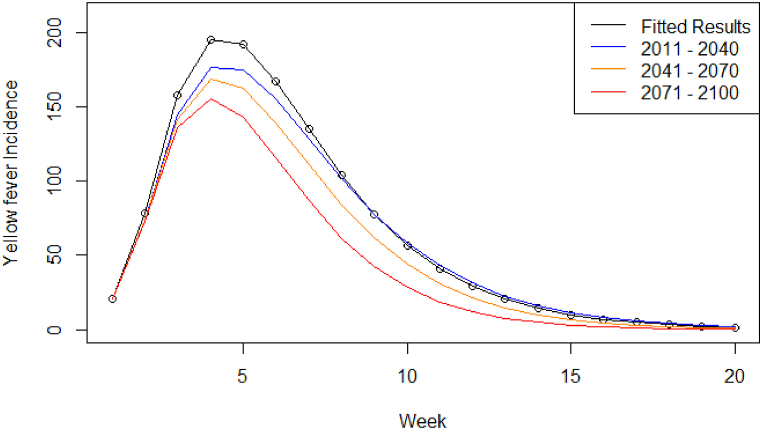
For RCP8.5 (Fig. 5), there was a 1.10-fold decrease in the peak number of cases between the 2017–2018 outbreak and the short-term time period (18 cases at peak), a 1.05-fold decrease between short- and medium-term (8 cases at peak), and a 1.08-fold decrease between medium- and long-term time periods (12 cases at peak), showing downward trend of YF cases in Brazil with increasing temperature. A similar pattern was observed for the cumulative incidence and estimated number of deaths. The number of weeks to the peak remained the same while the duration of the outbreak decreased as temperature increases (21–17 weeks) (Table 4).

Fig. 5.

Symptomatic infectious humans (compartment I) model output projected under RCP8.5, from 2011 to 2040 (blue), 2041–2070 (orange), and 2071–2100 (red), compared to the model output fitted to the 2017/18 YF virus outbreak (black circles and line).

Sensitivity analysis

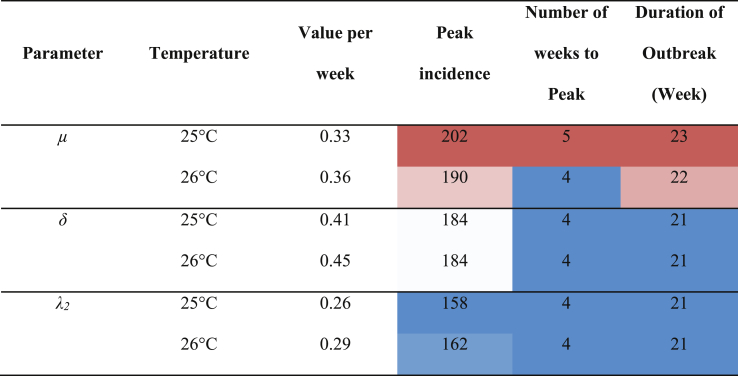
The death rate was the most influential parameter amongst the three climate-sensitive parameters reducing peak incidence by 12 cases (Table 5). There was no change to the development rate due to temperature. For EIP, the peak incidence increased slightly by 4 cases.

Table 5.

Results of the sensitivity analysis for the mosquito death rate (μ), mosquito development rate (δ), and EIP (λ₂), The parameter values were calculated using their respective relationships to temperature (Table 3, Fig. 2) at 25 °C and 26 °C. Each column is presented from blue (lowest value) to white (medium) to red (highest value).

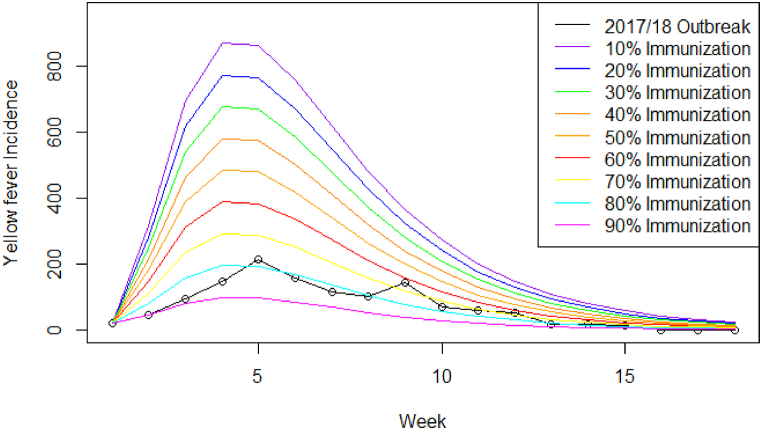
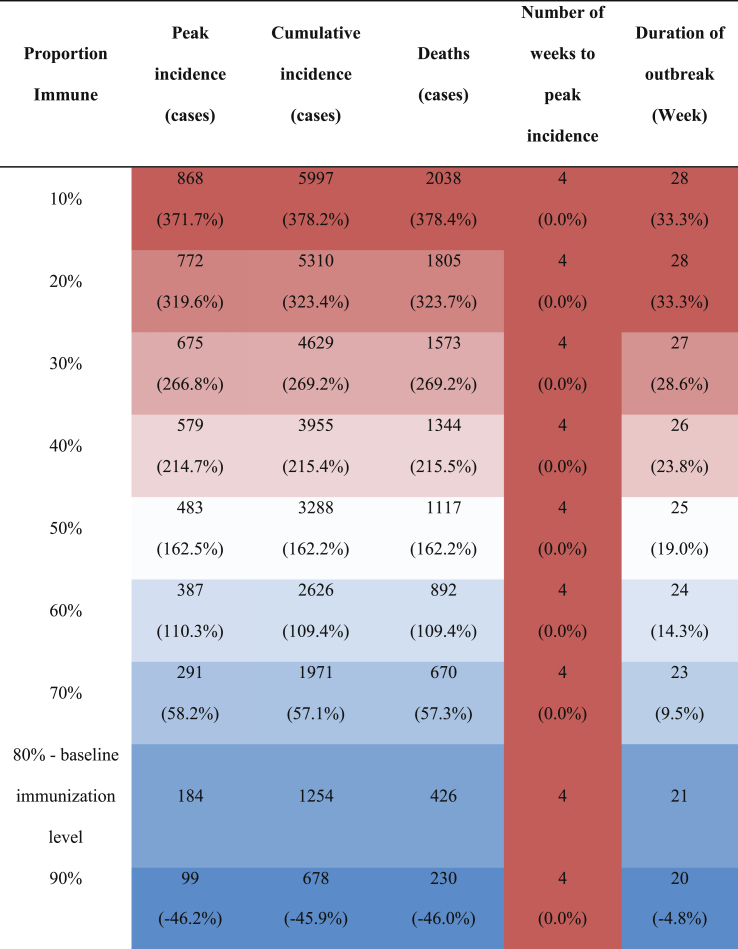
The proportion of the population with immunity had a substantial impact on the overall epidemic curve, resulting in a reduction in outbreak peak from 868 cases (10% immunity) to 99 cases (90% immunity) and the duration of the outbreak from 28 weeks (10% immunity) to 20 weeks (90% immunity) (Fig. 6 and Table 6).

Fig. 6.

Number of symptomatic infectious YF virus cases by week from the 2017/18 outbreak data (black dots and line) compared to modelled cases at 10% population (purple), 20% immunization (blue), 30% immunization (green), 40% immunization (dark orange), 50% immunization (orange), 60% immunization (red), 70% immunization (yellow), 80% immunization (cyan), and 90% immunization (magenta). The model was fitted using 80% immunization (cyan) which represents the closest fit to the observed data (Machado et al., 2013; Shearer et al., 2017).

Table 6.

Model outcomes (peak incidence, cumulative incidence, number of disease-induced deaths, number of weeks to peak, and duration of outbreak) for various proportion of immunized individuals (either natural or acquired). Each column is presented from blue (lowest value) to white (medium) to red (highest value). The percentages below the values are the percent change when the outcome value is compared to 80%, as that is the immunization level used in the model.

Discussion

The objective of this paper was to develop a mathematical model for YF virus transmission between humans and mosquitoes in Brazil and to determine how the epidemiology of the YF virus outbreak may change as a result of changing climatic conditions, which are expected to alter mosquito dynamics. Our key findings were that with increasing temperature, YF virus outbreaks in Brazil would decrease in duration and total incidence, with both values lower when compared to the 2017/18 outbreak. The reduction in the outbreak is contradictory to some previous modelling studies, which show the outbreak intensity of mosquito-borne diseases is likely to increase in locations similar to Brazil (Gaythorpe et al., 2020; Hamlet et al., 2018; Tesla et al., 2018). We also found that of all the temperature-sensitive parameters in the model, the mosquito death rate was more influential on model outcomes than the development rate and EIP. Finally, our YF vaccination analysis identified that outbreak intensity is closely linked to herd immunity; acquired either via infection or vaccination.

Our study showed for both RCP scenarios, the number of cases and outbreak duration reduced with increasing temperature. The reduction in cases and outbreak duration with increasing temperature is contrary to previous modelling studies which noted an increase in cases (Tesla et al., 2018; Gaythorpe et al., 2020; Hamlet et al., 2018). In a previous modelling study, it was noted that an increase in temperature would increase the cases of Zika virus in the Americas (Tesla et al., 2018), although this study was on Zika virus and Aedes spp. of mosquitoes, not YF virus and Haemagogus spp. The other studies were conducted on African YF virus and the same increase in cases with increasing temperature was noted (Gaythorpe et al., 2020; Hamlet et al., 2018). While the general patterns are the same, the development and death rate of Haemagogus spp. over temperature are different from Aedes spp (Marinho et al., 2016; Tesla et al., 2018). Research has indicated that, as temperature increases, Haemagogus mosquito development rate increases linearly, while the mosquito death rate was parabolic and declined until 25 °C before increasing (Bates, 1947) (Fig. 2). Although our findings are contrary to previous studies, it does have similar findings to some. A modelling study in Australia noted a reduction in the incidence and duration of dengue due to increasing temperature. The authors indicated that the decrease may be due to higher mosquito death; although, the mosquito vector used in the model was Aedes aegypti rather than Haemagogus spp. (Williams et al., 2016). Another study was conducted in Africa, and noted that with increasing temperature, African climate may become more suitable for Aedes spp. of mosquitoes and the transmission of arboviruses, such as dengue, rather than Anopheles spp. of mosquitoes and malaria (Mordecai et al., 2020). Thus, it is possible that a humid tropical/sub-tropical region, like Brazil, may also experience a change in the incidence of disease, due to changes in the suitability of the climate to the different mosquito species.

We found that the mosquito death rate was more influential on the model output than mosquito development rate and EIP. This could further explain the decrease in the number of cases as temperature increases, because the number of mosquitoes that survive the EIP diminishes. This would reduce the population of infectious mosquitoes and, in turn, transmission. Another study found the mosquito lifecycle to be important in explaining dengue outbreaks, as infected mosquitoes must survive the length of the EIP before they are able to spread dengue (Lee et al., 2018), and while this study was conducted on Aedes spp., Haemagogus spp. must also survive the length of the EIP before being able to transmit YF virus.

Finally, our findings on the impact of vaccination on the model outcomes showed that the proportion of individuals with immunity (either naturally acquired or via vaccination) significantly influenced the model outcomes. Similar findings have been shown for the African strain of YF virus where a national vaccination campaign increased vaccination uptake by 70% which subsequently reduced the number of cases by 5.6-fold (Zhao et al., 2018).

Our study is not without limitations. First, we assumed that the intrinsic incubation period and recovery rate were the same for both symptomatic and asymptomatic individuals, thus we could have overestimated the values of these parameters, as it is likely these values are reduced for an asymptomatic individual. Next, we used some simplifying assumptions and did not capture Brazil’s population or geographic heterogeneity, or stochasticity, which can influence parameters in the model (Carlson et al., 2016; Perkins et al., 2016). Our model also did not consider changes that may occur over time in Brazil, such as socio-economic status, urbanization, deforestation and other land changes, which have an impact on both exposure and mosquito-borne diseases by introducing more cases as contact between human and mosquito populations increases (Chaves et al., 2018; Lambin et al., 2010; MacDonald & Mordecai, 2019). Previous studies have noted that precipitation impacts mosquito-borne diseases by creating or destroying potential egg-laying locations (Alto & Juliano, 2001; Lega et al., 2017). Precipitation in Brazil is expected to decrease under future climate conditions (IPCC, 2014). The interaction between precipitation and temperature, and the subsequent impact on Haemagogus spp. of mosquitoes is currently unknown and may have impacted our model results. Although this is the case, the amount of uncertainty is high in climate models regarding precipitation over tropical areas, especially for extreme rainfall over continental areas (IPCC, 2013; Kent et al., 2015; Wootten et al., 2017). Further research is required using precipitation from CORDEX runs. Despite our model’s simplicity, it can be used as a framework for more complex models.

Further research should be conducted on Haemagogus spp. of mosquitoes, as little is known about how the increasing temperature will impact their development, death rate and EIP, and the papers describing these values may be outdated (Bates, 1947; Bates & Roca-Garcia, 1946). Additionally, region-specific or heterogeneous models could be created, including parameters, that are different across Brazil, both at the present climate and future climate. Further research could be conducted to determine which regions may be more likely to experience an increase in cases and which would experience a decrease in cases, based on such variables as climate and geography.

Conclusion

We projected YF outbreaks in Brazil based on the 2017/18 outbreak under two climate change scenarios. We found that the increase in temperature in subtropical/tropical countries, such as Brazil, results in a potential reduction in YF peak incidence, cumulative incidence, outbreak duration, and the number of weeks to the peak to levels below the intensity of the 2017/18 outbreak. Based on these findings, we anticipate that future outbreaks of YF in Brazil will be less intense, due to parts of Brazil becoming unsuitable for Haemagogus spp. of mosquitoes to survive, and suboptimal for YF virus replication under climate change. While the reduction in outbreak intensity is positive, it is important to remember that the impact of climate on mosquito-borne diseases involves multiple factors beyond temperature, such as precipitation and future land use, and that Aedes spp. can also transmit the YF virus. Additionally, different countries with different climate or geography may experience an increase in outbreak sizes, rather than a decrease, highlighting the importance of context when planning for public health inventions and future strategies. Our study provides a baseline for modelling YF in Brazil using Haemagogus spp. as the mosquito vector and highlights the need for further study on these mosquito species.

Involvement of funding source

The PhD candidate’s (TS) stipend was provided by the Public Health Agency of Canada (PHAC). VN is TS’s co-supervisor and an employee of PHAC.

Declaration of competing interest

There are no conflicts of interest to disclose.

This research required no ethics approval as it only used publicly available unidentifiable data.

Handling editor. Dr HE DAIHAI HE

Appendix. 1

In the simulation, humans move through the compartments from the susceptible compartment (compartment S) to exposed compartment (compartment E), to the infectious compartments (either symptomatic, compartment I, or asymptomatic, compartment A), and finally to either the recovered compartment (compartment R) or the disease-induced death compartment (compartment D). The mosquitoes move from the susceptible compartment (compartment X) to the exposed compartment (compartment Y), and then to the infectious compartment (compartment Z). When infectious mosquitoes bite susceptible humans, successfully infected humans move from compartment S to compartment E. When susceptible mosquitoes feed on infectious humans (compartments I and A), a proportion of the mosquitoes move from compartment X to compartment Y. Individuals remain in the recovered compartment after infection as humans have life-long immunity to the disease (Monath, 2001). These dynamics are described with the following ordinary differential equations, where the parameters and initial conditions are outlined in Table 1, Table 2 respectively:

$$\frac{dS}{dt}=-{\beta }_{1}SZ$$

$$\frac{dE}{dt}={\beta }_{1}SZ-{\lambda }_{1}E$$

$$\frac{dI}{dt}=\phi {\lambda }_{1}E-\gamma I-\omega I$$

$$\frac{dA}{dt}=(1-\phi ){\lambda }_{1}E-\gamma A$$

$$\frac{dR}{dt}=\gamma (I+A)$$

$$\frac{dD}{dt}=\omega I$$

$$\frac{dX}{dt}=\delta M-{\beta }_{2}X(I+A)-\mu X$$

$$\frac{dY}{dt}={\beta }_{2}X\left(I+A\right)-{\lambda }_{2}Y-\mu Y$$

$$\frac{dZ}{dt}={\lambda }_{2}Y-\mu Z$$

Appendix. 2

Table A.1.

The ten simulations used in this study from Regional Climate Models (RCMs) driven by different Coupled Global Climate Models (GCMs). The simulations use the two Representative Concentration Pathways (RCP4.5 and RCP8.5). This South American climate data was obtained from the CORDEX-SAM44 database (CORDEX-SAM44, n.d.). All RCMs use a grid at around 0.44° of horizontal resolution.

Regional Climate Model	Driven conditions from Coupled Global Climate Model (CGCM)	Institution for CGCMs
RCA4-v3 from the Rossby Centre regional atmospheric model (RCA4; Strandberg et al., 2014)	CSIRO-QCCCE-CSIRO-Mk3-6-0	The Commonwealth Scientific and Industrial Research Organisation (CSIRO, Australia) and Queensland Climate Change Centre of Excellence (QCCCE), Australia
	CCCma-CanESM2	Canadian Centre for Climate Modelling and Analysis (CCCma), Canada
	IPSL-IPSL-CM5A-MR	Institut de recherche en sciences de l’environnement (IPSL), France
	NCC-NorESM1-M	Norwegian Climate Centre (NCC), Norway
	ICHEC-EC-EARTH	Irish Centre for High-End Computing (ICHEC), Ireland
	MPI-M-MPI-ESM-LR	Max Planck Institut für Meteorologie (MPI), Germany
	NOAA-GFDL-GFDL-ESM2M	National Oceanic and Atmospheric Administration (NOAA), United States of America
	MIROC-MIROC5	Model for Interdisciplinary Research on Climate (MIROC), Japan
	MOHC-HadGEM2-ES	Met Office Hadley Centre (MOHC), United Kingdom
REMO2009 from the Climate Service Centre Germany (GERICS); Jacob et al. (2012)	MPI-M-MPI-ESM-LR	MPI, Germany