Fig. 2. The illustration of the fundamental concepts in TDA.

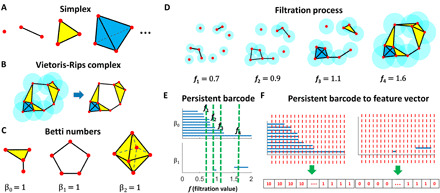
(A) k-simplex is a convex hull made from k + 1 vertices. Geometrically, they can be viewed as a point (0-simplex), an edge (1-simplex), a triangle (2-simplex), and a tetrahedron (3-simplex). (B) In Vietoris-Rips complex, spheres are assigned to each data point, and a k-simplex is formed among a set of k + 1 vertices if any two spheres among k + 1 spheres overlap with each other. (C) Geometrically, β₀ is the number of connected components, β₁ is the number of circles or loops, and β₂ is the number of voids or cavities. (D) Illustration of a filtration process. Simplicial complexes at four different filtration values represent interactions at four different scales. (E) Persistent barcode generated from the filtration process in (D). (F) Persistent barcode–based featurization using a binning approach.