Abstract
Neuronal activity depends on ion channels and biophysical processes that are strongly and differentially sensitive to physical variables such as temperature and pH. Nonetheless, neuronal oscillators can be surprisingly resilient to perturbations in these variables. We study a three-neuron pacemaker ensemble that drives the pyloric rhythm of the crab, Cancer borealis. These crabs routinely experience a number of global perturbations, including changes in temperature and pH. Although pyloric oscillations are robust to such changes, for sufficiently large deviations the rhythm reversibly breaks down. As temperature increases beyond a tipping point, oscillators transition to silence. Acidic pH deviations also show tipping points, with a reliable transition first to tonic spiking, then to silence. Surprisingly, robustness to perturbations in pH only moderately affects temperature robustness. Consistent with high animal-to-animal variability in biophysical circuit parameters, tipping points in temperature and pH vary across animals. However, the ordering and discrete classes of transitions at critical points are conserved. This implies that qualitative oscillator dynamics are preserved across animals despite high quantitative parameter variability. A universal model of bursting dynamics predicts the existence of these transition types and the order in which they occur.
Significance
Biological oscillators are important for many physiological processes. A three-neuron ensemble in the stomatogastric ganglion of decapod crustaceans controls vital digestive contractions known as the pyloric rhythm. These neural circuits show considerable variability in the number of each kind of voltage- and time-dependent ion channel across animals. Because all ion channel function is affected by global perturbations such as temperature or pH, it is remarkable that cold-blooded animals are resilient to these environmental challenges. We show that the oscillator makes stereotyped state changes in response to temperature and pH but that the two perturbations do not interact strongly. This is predicted by a universal mathematical model of neural oscillations.
Introduction
All nervous systems need to combat fluctuations in their environment that might disrupt neuronal and circuit activity. Fluctuations in global physical variables such as temperature and pH are usually resisted by compensatory homeostatic responses and behavioral preferences (1, 2, 3, 4, 5, 6, 7). In addition to active mechanisms that maintain homeostasis, neural circuits exhibit intrinsic, automatic robustness to perturbations that arise from the collective properties of the conductances that they express (8), providing an additional line of defense against circuit failure (9, 10, 11, 12).
Recent work in crustacean nervous systems shows that the neural circuit that generates the pyloric rhythm in the stomatogastric ganglion (STG) of the crab, Cancer borealis, can maintain normal activity patterns despite changes in temperature from below 7 to ∼25°C (2,10, 11, 12, 13). This robustness makes sense ecologically because crustaceans such as crabs and lobsters are poikilotherms—they do not regulate their body temperature precisely—and experience natural variations in temperature in their habitat. However, all biochemical reactions are temperature dependent, so every physiological property that underpins neuronal and circuit function will be altered by a temperature change. For this reason, we refer to a temperature perturbation as a global perturbation.
There are several surprising aspects of the STG’s robustness to acute changes in temperature. The underlying physiological properties of the neurons show large and heterogeneous temperature sensitivities that differ severalfold between different currents and gating variables (11). Without constraints on channel expression relationships, such strong and heterogeneous temperature dependence would detune physiological properties and cause circuit failure for even modest temperature changes (4,14,15). Nonetheless, there is two- to sixfold variability in the expression of the different ionic conductances within the same identified neurons of the STG across different animals (16, 17, 18, 19). Therefore, any mechanism that tunes conductance expression to avoid temperature-induced instability must also allow large variation in the space of solutions it finds.
Together, these observations suggest that robustness to temperature imposes a constraint on the physiological properties of individual neurons and circuits. An immediate question is whether such a constraint might be satisfied only at the cost of making the circuit vulnerable to other kinds of global perturbations. A key question we address here is how temperature robustness interacts with robustness to other global perturbations that alter neuronal and circuit properties distinctly from temperature. Surprisingly, we find only a modest interaction between pH and temperature on neural oscillator activity, suggesting that each preparation, despite having idiosyncratic properties, has tuned these properties to ensure robustness to multiple external insults.
Recent theoretical work has shown how correlations in conductance expression can reconcile biophysical variability with behavioral robustness, provided the correlations are constrained to offset the sensitivity of circuit behavior to channel properties (15). This, in turn, suggests that neuronal oscillators owe their robustness to certain universal dynamics that force a system to oscillate despite substantial cellular and circuit level variability in biophysical parameters (20, 21, 22). If true, such universal dynamics would lead to stereotyped transitions when oscillatory dynamics fails because of global perturbations in variables such as temperature and pH, even if these transitions occur at markedly different temperatures and pH values in each animal. We explicitly test this hypothesis here and find that observed transitions in dynamics are predicted by a universal model of neuronal excitability.
Neuronal oscillators are critical for the operation of many circuits. Oscillators have a number of properties that are easy to measure and evaluate providing an outstanding test bed for the assessment of resilience to single or multiple global perturbations. Consequently, in this study we used a three-neuron oscillator that functions to drive the pyloric rhythm in the STG. We subjected the same recorded neuronal oscillators to simultaneous temperature and pH variations. pH has similar widespread effects on ionic currents, reversal potentials and channel kinetics as temperature (23, 24, 25, 26, 27), although the effects of pH on individual physiological variables in the STG are not as well characterized as those of temperature (28). Moreover, there is some evidence that crabs and other marine organisms may experience acute changes in pH in their environment, suggesting that these neurons may be adapted to cope with this perturbation (29, 30, 31). We developed a means of quantifying internal variability in the oscillator that is predictive of the eventual collapse of oscillator rhythm, albeit to a limited extent.
Materials and Methods
Animals
C. borealis were purchased from Commercial Lobster (Boston, MA) and maintained at 11°C in tanks containing artificial seawater. Animals used in this study were obtained between July 2016 and November 2017.
Solutions
C. borealis physiological saline was composed of 440 mM NaCl, 26 mM MgCl2, 13 mM CaCl2, 11 mM KCl, 12 mM Trizma Base, and 5 mM maleic acid (pH 7.4–7.5, measured at room temperature). For more acidic saline, pH was adjusted with additional maleic acid. Picrotoxin (PTX) was purchased from Sigma (St. Louis, MO) and used at 10−5 M in physiological saline. The microelectrode solution was 10 mM MgCl2, 400 mM potassium gluconate, 10 mM Hepes, 15 mM NaSO4, 20 mM NaCl (pH 7.45) (29).
Electrophysiology
The stomatogastric nervous system was dissected from the animal and pinned taut in a Sylgard (Dow Corning, Midland, MI)-coated plastic petri dish containing chilled physiological saline. All preparations used had intact inferior and superior esophageal nerves and included commissural and esophageal ganglia. For the duration of experiments, the dish was superfused with saline. Temperature was controlled using a Peltier device (Warner Instruments, Hamden, CT) and monitored using a thermistor probe placed in the dish. Vaseline wells were placed around the lateral ventricular nerve and the pyloric dilator nerve, and extracellular recordings were obtained using stainless steel pin electrodes placed in the wells and amplified using a differential amplifier (A-M Systems, Sequim, WA). In addition, intracellular recordings were obtained from the pyloric dilator (PD) somata using 15–25 M glass microelectrodes pulled with a Flaming/Brown micropipette puller (Sutter Instrument Company, Novato, CA). The cell type was identified by comparing spiking activity to extracellular recordings on the PD nerve and by examining the intracellular waveform.
Temperature manipulations
Intracellular recordings were begun at either 25 or 5°C below a crash temperature determined with extracellular recordings. Preparations were then exposed to continuously increasing temperatures, referred to as temperature ramps. A waveform generator (Rigol, Beijing, China) was used to create a steadily increasing voltage to control the output of the Peltier device. Temperature was increased until preparations changed from bursting to silence without continuous bursting/spiking activity, at which point the temperature ramp was stopped in a majority of experiments.
As previously reported, somata swelled with increasing temperature (10,13). With increasing temperature, small adjustments to the location of the intracellular electrode were made to maintain the recording.
All preparations analyzed, with the exception of the experiments shown in Fig. 5 B, were selected based on the presence of the transition to silence. Preparations that continued to burst past 34°C were excluded.
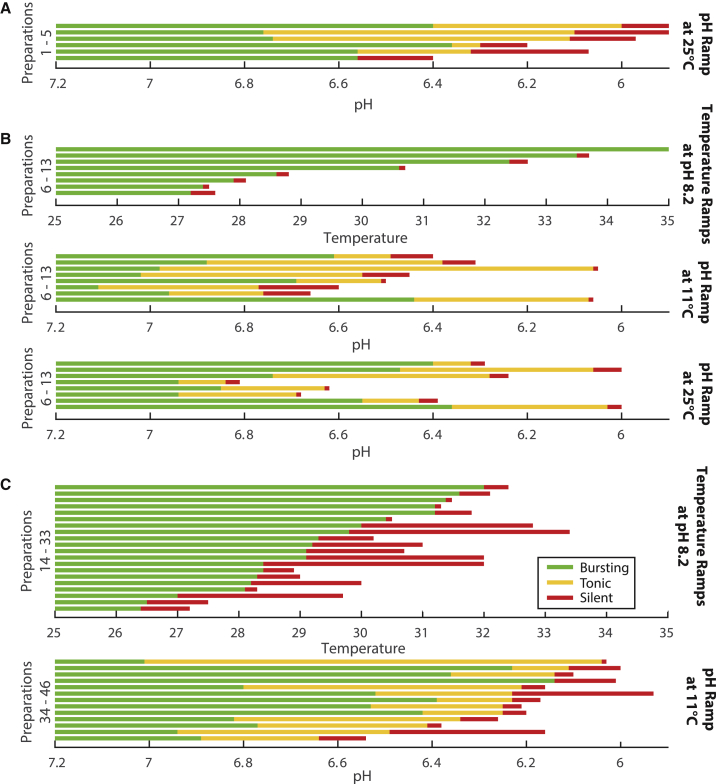
Figure 5.
Qualitative type and orderings of transitions are preserved despite large animal-to-animal variability in critical temperatures and pH. (A) Each horizontal line represents one preparation exposed to a range of pH at 25°C (n = 5). The qualitative activity pattern, or state, is indicated with color: green corresponding to bursting, yellow to tonic spiking, and red to silence. (B) The same preparation was exposed to each condition and plotted in the same order across conditions (n = 8), meaning the first horizontal line in the temperature conditions corresponds to the first horizontal line in the pH conditions. (C) The top set of preparations were exposed to increasing temperature (n = 20, 13 from Figs. 2 and 7 additional without intracellular recordings), and the bottom set of preparations were exposed to decreasing pH (n = 15). (A–C) Preparations are ordered based on transition to silence. To see this figure in color, go online.
pH manipulations
Intracellular recordings of the PD neuron were begun at physiological pH. After the addition of PTX, the pH of the superfused saline was controlled by a slow, continuous mixing of pH 7 and pH 5 physiological saline during the experiments. The pH of the superfused saline was measured using a pH microelectrode purchased through Thermo Fisher Scientific (Orion 9810BN; Waltham, MA). The probe was calibrated each day using reference solutions at 11 and/or 25°C.
Data analysis
Data were acquired using a Digidata 1440 data acquisition board (Axon Instruments, San Jose, CA) and analyzed using MATLAB (The MathWorks, Natick, MA).
Transition definitions
Discrete transition points were defined in both the pH and temperature experiments, with similar definitions used in both. A transition was marked when a preparation spent more than 20 out of 30 s period in any activity pattern. This reliably captured switches from one activity pattern to another while filtering out small flickering events between activity patterns that occur in small ranges (<0.5°C or <0.2 pH) near transitions.
Phase plane analysis
The stretches of data to be analyzed were first low-pass filtered to remove spikes. The filtered voltage signal and its derivative were normalized by the standard deviation (SD) of each respective signal. The signal was mean subtracted to center the oscillation on the origin of the axes and then transformed from a Cartesian coordinate system (with the normalized voltage signal on the x axis and the normalized voltage derivative on the y axis) to polar coordinates. These steps generate the phase portrait shown in Fig. 4 C.
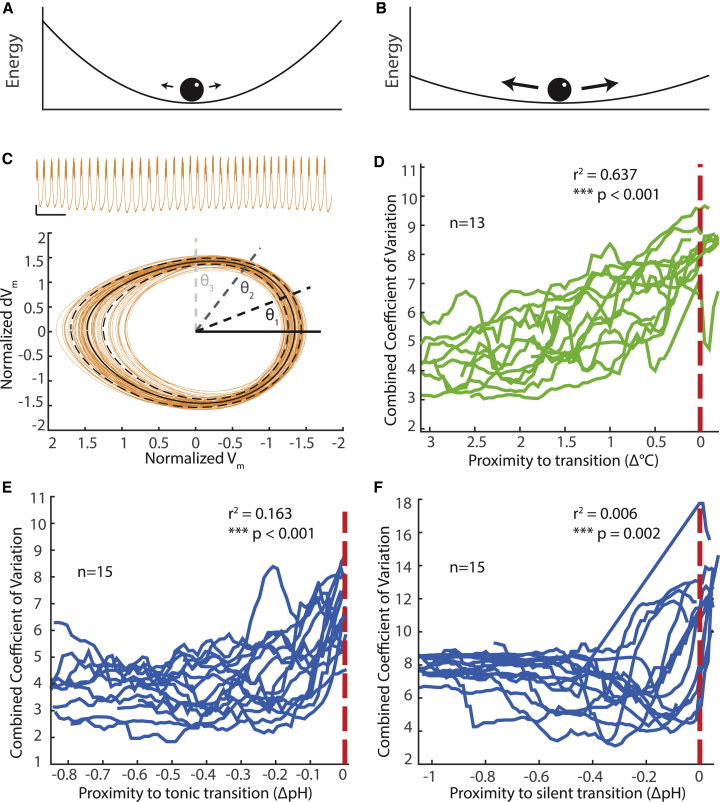
Figure 4.
Variance increases at the population level before transitions in activity pattern. (A and B) Cartoon schematic depicting noisy ball attracted to bottom of trough. The same amount of noise induces larger deviations in (B) compared with (A). (C) Above: voltage trace from PD neuron in isolated pacemaker plotted in orange. Scale, 1 s, 5 mV at −50 mV. Below: phase portrait generated from low-passed voltage trace plotted in orange as normalized membrane voltage (Vm) versus normalized instantaneous change in voltage (dVm; see Materials and methods). The solid black line represents the mean of the oscillations, and the dashed black lines are two SDs plus and minus the mean. These values—means and SDs—are calculated for 200 points in phase schematized by the solid and dashed black and gray lines. (D) Each green line represents the moving average of combined coefficients of variation (see Materials and methods) plotted as a function of temperature from transition to silence (red line). (E and F) Each blue line represents the moving average of combined coefficient of variation as a function of pH. Experiments are aligned to transition. (E) Red line represents transition to tonic spiking. (F) Red line represents transition to silence. (D–F) Linear regression on log-transformed data predicting CCV using proximity to transition. To see this figure in color, go online.
Next, we calculated the average trajectory of the oscillations by taking the mean and SD of the radial coordinate at 200 evenly spaced angular coordinates. This gave the envelope plotted in the phase plane in Fig. 4 C. From these values, we calculated the coefficient of variation, the SD normalized to the mean, at each point in the phase of the oscillation. We then combined the values by taking their root mean-square, and these values were plotted in Fig. 4, B–D after being smoothed by taking a 0.5°C or 0.1 pH moving average.
Statistical methods
Statistical analysis was performed using MATLAB. Coefficients of variation were compared as log-transformed variance as previously reported (13). Residuals of fits were inspected and confirmed to have an approximate normal distribution.
The linear model in Fig. 5 was fitted using fitlme in MATLAB. We chose a linear mixed effects model with fixed effects accounting for trends among the population and the random effects capturing interpreparation variability. The model was specified to describe transition pH as a function of transition temperature and transition type with interaction terms between temperature and transition type and random effects of preparation on both (i.e., pH ∼1 + temperature × transition_type + (1 + temperature = transition_type |preparation_id).
Numerical methods
Simulated model behavior for the normal form is described by the systems of (1a), (1b), (1c) and (2a), (2b), (2c) in the Results. This was done using numerical integration in the Julia DifferentialEquation.jl package. To simulate the effect of stochastic channel dynamics, a noise term was added to the second variable of the normal form, and the resulting simulations were obtained using an out-of-the-box stochastic differential equations solver with default parameters. In deterministic simulations, noise amplitude was set to zero. In noisy simulations, noise amplitude was set to D = 0.001. Other parameters are as follows. In all parameter regimes: εs = 0.01, εu = 0.0001, and γ = −0.1. Parameter regime A: βf = 0.3, βs = 0.15, and Iapp = −0.337. Parameter regime B: βf = 0.25, βs = 0.285, and Iapp = −0.202. Parameter regime C: βf = −0.05, βs = 0.35, and Iapp = 0.0. Parameter regime D: βf = 0.05, βs = 0.145, and Iapp = −0.393. Parameter regime E: βf = −0.033, βs = 0.11, and Iapp = −0.366.
Results
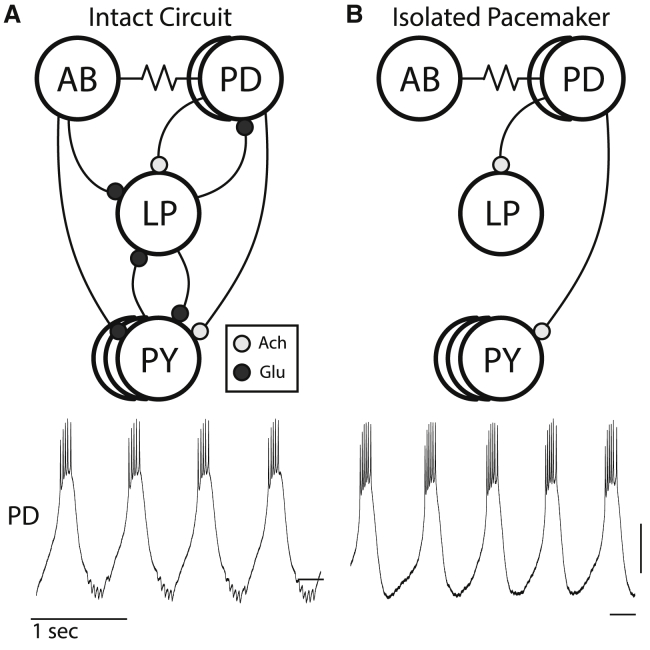
The pyloric rhythm in the STG is driven by a subset of identified neurons that comprise a so-called pacemaker kernel, or oscillator, consisting of the electrically coupled double PD and single anterior burster neurons. The anterior burster neuron is an intrinsically bursting cell and the source of the oscillation. The pacemaker kernel rhythmically inhibits the LP (lateral pyloric) and pyloric neurons, as depicted in Fig. 1 A. The LP neuron feeds back onto and inhibits the PD neurons using glutamatergic transmission. The LP-evoked inhibitory postsynaptic potentials in the PD neuron are seen in the intracellular recordings shown in Fig. 1 A.
Figure 1.
The pyloric and isolated pacemaker circuits. (A) Above: circuit diagram of the pyloric network of the STG. Chemical synapses are represented by curved lines with colored balls, with red indicating a cholinergic synapse and blue a glutamatergic synapse. Electrical synapses are represented by resistor symbols. Below: an intracellular recording of the PD neuron from the intact pyloric circuit. (B) Above: circuit diagram of the isolated pacemaker after the addition of PTX. Below: intracellular recording of the PD neuron from the isolated pacemaker circuit. Scale, 10 mV with dash at −50 mV.
For this study, we isolated the oscillatory pacemaker kernel from the rest of the circuit by adding PTX, which blocks glutamatergic transmission in the STG (Fig. 1 B; (32)). In PTX, glutamatergic inhibitory postsynaptic potentials are no longer present in recordings from either of the PD neurons during the stable oscillation (Fig. 1 B, bottom panel).
Oscillator activity near critical temperatures
We examined the activity of the pacemaker kernel in response to acute changes in temperature. Previous work established that the pacemaker oscillation fails above a critical temperature (13). We roughly determined the temperature at which the intact pyloric rhythm became disorganized or silent using extracellular recordings. We denote this the critical temperature or transition point. Consistent with previous work, many preparations are robust across large changes in temperature that prohibit a stable intracellular recording for the full temperature range.
In 13 preparations, we first determined the approximate critical temperature in the intact circuit. We then set the temperature of the bath solution to 5°C below the transition point, applied picrotoxin, and obtained intracellular recordings from a PD neuron in the isolated oscillator. The temperature was then slowly increased at a rate of ∼5°C per hour while holding the intracellular recording, allowing us to monitor changes in the activity patterns of the isolated oscillator with small changes in temperature (Fig. 2).
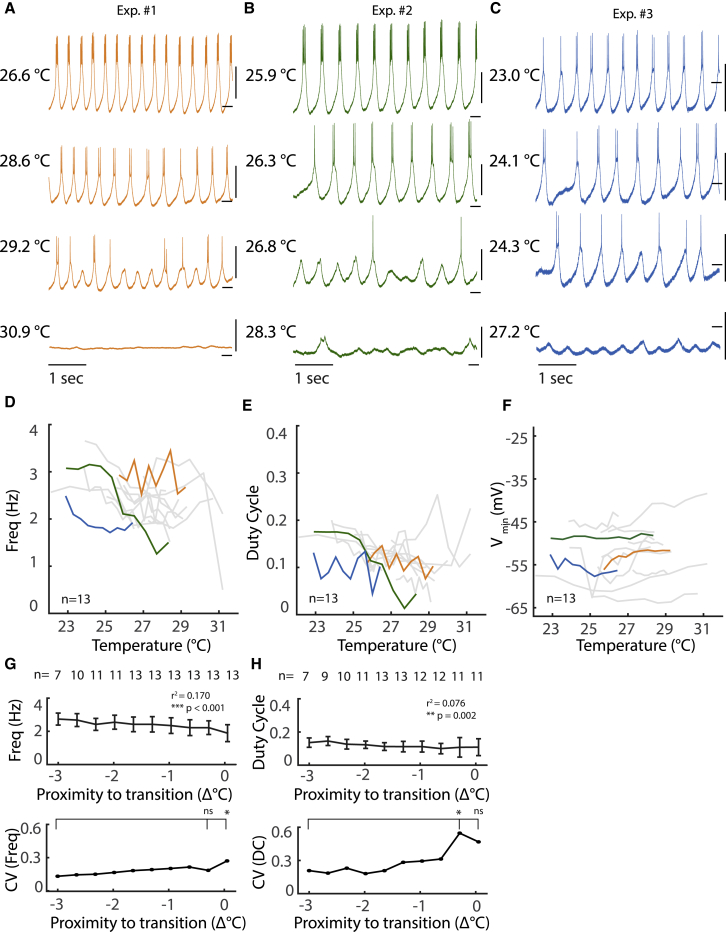
Figure 2.
Activity of isolated pacemaker near critical temperatures. (A–C) Intracellular recordings of the PD neuron in the presence of PTX across a range of temperatures. Scale, 10 mV with dash at −50 mV. (D–F) Burst frequency (D), duty cycle (E), and minimal voltage during oscillation (F) of PD neuron from 13 preparations are plotted as a function of temperature. Duty cycle is computed from intracellular traces as burst duration normalized to period of oscillation. Duty cycle becomes undefined for single spike bursts. Colored lines correspond to example experiments with the same colors in (A)–(C). (G–H) Above: average burst frequency (G) and duty cycle (H) across preparations are plotted as a function of distance, in degrees Celsius, to transition to silence. Error bars represent SDs. Not all cells were recorded for full 3° before transition (see Materials and methods). Below: coefficients of variation for burst frequency and duty cycle, respectively, calculated from above plots and aligned to transition to silence. ∗p < 0.05; ns, not significant. (G, top) Frequency is predicted by proximity to transition using linear regression; (bottom) p = 0.0342, two-sample F-test for equal variance. (H, top) Duty cycle is predicted by proximity to transition using linear regression; (bottom) p = 0.0069, two-sample F-test for equal variance. To see this figure in color, go online.
Recordings from three example experiments are shown in Fig. 2, A–C. When far from critical temperatures, the isolated oscillator had relatively constant burst frequency, with clear membrane potential plateaus and bursts of action potentials. As temperature was increased, bursting became less regular, leaving plateaus with few or no spikes and variable interburst intervals. Qualitative changes in bursting of the pacemaker, i.e., transition points, were observed across small changes in temperature.
Across preparations, these qualitative changes occurred at different temperatures. In Fig. 2 A, for example, there is a change in activity patterns of the preparation between 29.2 and 31°C, with bursting activity ceasing at the higher temperature. In this preparation, there is little qualitative change between 26.6 and 28.6°C, which can be contrasted with the changes in the preparation shown in Fig. 2 B, in which there is a dramatic change in activity pattern of the pacemaker from 26.3 to 26.8°C. In each preparation, as temperature was increased further, activity patterns transitioned to silence, with no spikes fired and only small fluctuations in the membrane potential (Fig. 2, A–C, bottom traces).
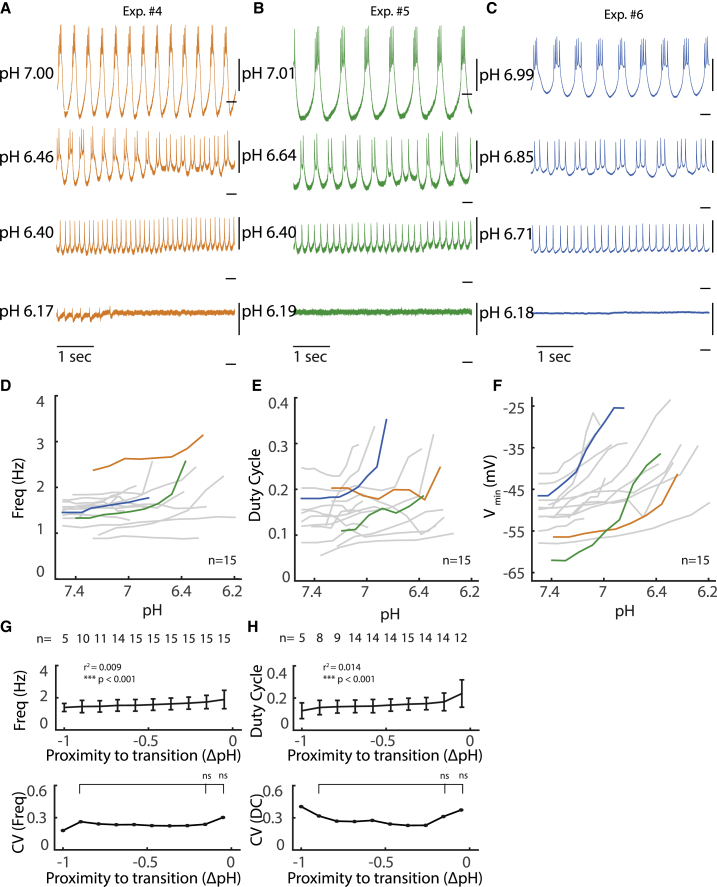
To quantitatively examine the changes in activity of the isolated oscillator near critical temperatures, we measured the burst frequency, duty cycle, and minimal membrane potential as a function of temperature (Fig. 2, D–F) and relative to the transition point to silence (Fig. 2, G and H). Duty cycle, important for the motor control function of this circuit, is defined as the duration of time spiking normalized to the burst period. It has previously been shown to be conserved over temperature ranges that permit a stable oscillation (11,13).
It has previously been shown that the burst frequency of the isolated oscillator increases with temperature between 10 and 25°C (11,13). When examining burst frequency near critical temperatures, we found that this relationship was not present (Fig. 2 D) because there was no consistent increase in frequency with increasing temperature across preparations. In addition, when data were aligned to transition to silence, mean frequency across preparations decreases as preparations approach the transition (p < 0.001, R2 = 0.17, linear regression), with increasing between-preparation variability (Fig. 2 G; p = 0.034, two-sample F-test for equal variance). Furthermore, duty cycle becomes more variable between preparations near critical temperatures (Fig. 2 E), and when aligned to the transitions to silence, we saw that there is greatly increased variability between preparations near critical transitions (p = 0.007, two-sample F-test for equal variance). Previous work in our lab examining transitions in activity patterns near critical temperatures found little evidence for hysteresis (10,11).
Activity of isolated pacemaker near critical pH
To contrast temperature-induced changes with those induced by a second global perturbation, we examined the effects of acidic pH on the isolated oscillator. Recent work has shown that the pyloric rhythm continues in the presence of extreme pH in an approximate range from pH 6.1 to pH 8.8 and that below approximately pH 6, the pyloric rhythm becomes silent (33). We sought to examine what occurs near these critical pH levels. To do this, we obtained intracellular recordings of the PD neuron in physiological saline at 11°C (pH 7.8). pH was then slowly lowered by continuously adding pH 5 saline to the volume of saline feeding the bath, with the rate of mixing adjusted to create a change to pH 6 over the course of 1 h.
Example traces from three experiments are shown in Fig. 3, A–C. All preparations were bursting at pH 7 (Fig. 3, A–C, top traces), but at more acidic pH, the regularity of this bursting changed, with preparations depolarizing and the amplitude of the slow wave decreasing (Fig. 3, A–C). At lower acidic pH, bursting became intermittent with periods of tonic spiking, and eventually the isolated oscillator transitioned fully to tonic spiking activity (Fig. 3, A–C, middle). After this transition, further decreases in pH caused additional depolarization and smaller amplitude spikes, and finally, the tonic spiking pattern transitioned to silence (Fig. 3, A–C). We therefore defined two critical pH values for each of these qualitative transitions in activity, one marking the transition from bursting to tonic spiking and one marking tonic spiking to silence.
Figure 3.
Activity of isolated pacemaker in acidic pH. (A–C) Intracellular recordings of the PD neuron in the presence of PTX across range of acidic pH. Scale, 10 mV with dash at −50 mV. (D–F) Burst frequency (D), duty cycle (E), and minimal voltage during oscillation (F) of PD neuron are plotted as a function of pH from 15 preparations. Duty cycle is computed as in Fig. 2. Colored traces correspond to example experiments of the same color in (A)–(C). Frequency and duty cycle are only plotted when cell is bursting. (G) Above: average burst frequency (G) and duty cycle (H) across preparations plotted as a function of distance to transition to tonic spiking. Error bars represent SDs. Not all cells were recorded for a range of 1 pH. Below: coefficients of variation for burst frequency and duty cycle, respectively, calculated from the above plot and aligned to transition to tonic spiking. ∗p < 0.05; ns, not significant. (G, top) Frequency is predicted by proximity to transition using linear regression; (bottom) p = 0.3757, two-sample F-test for equal variance. (H, top) Duty cycle is predicted by proximity to transition using linear regression; (bottom) p = 0.2893, two-sample F-test for equal variance. To see this figure in color, go online.
To compare the effects of pH and temperature near critical points (Fig. 2, D–H), we examined the relationship of pH with burst frequency, duty cycle, and minimal voltage during oscillations (burst frequency and duty cycle are only defined during bursting). In the range examined here, there is a slight effect of pH on burst frequency; with a positive trend in frequency, pH becomes acidic (Fig. 3, D and G; R2 = 0.009, p < 0.001, linear regression). Duty cycle near critical pH is variable, with a trend toward preparations having increased duty cycle before transition to tonic spiking (Fig. 3, E and H, p < 0.001, linear regression). In contrast to preparations near critical temperatures (Fig. 2 F), changes in pH cause substantial depolarization (Fig. 3 F; p < 0.001, one-tailed unpaired t-test on data aligned to transition to silence). When examining the system for hysteresis around critical pH, we found evidence for a significant time lag lasting many minutes that masked any practically observable pH-dependent hysteresis (Fig. S1). Such a time lag may, for example, reflect finite mixing and equilibration times that exist despite careful placement of pH probes and optimization of flow rates in the recording chamber.
Together, the qualitative and quantitative differences between pH- and temperature-induced changes in membrane potential activity are consistent with these perturbations having distinct, global effects on underlying membrane currents, as shown in previous work (23,24,28,34).
Predicting transitions in the oscillator
We have shown that near critical temperatures and pH, the activity patterns of the isolated oscillator change abruptly with critical points varying across preparations. There is a body of theory (35, 36, 37, 38, 39) that proposes a set of generalized markers to predict critical transitions in dynamical systems, including complex biological systems. These markers include increased variability, increased recovery time from perturbation, and flickering between states. We therefore analyzed membrane potential variability near transitions, attempting to predict the precise transition points in the activity patterns of the isolated pacemaker.
Increased variability is depicted in Fig. 4, A and B using an example system consisting of a ball in a trough, subject to noisy perturbations. This system is stably attracted to the lowest energy state, whereas noise moves the ball randomly away from this stable point. As the system moves closer to reorganizing, thereby gaining a new stable state, the basin of attraction becomes shallower (Fig. 4 B). The same amount of noise now generates greater variation in the movement of the ball. This simple example illustrates why increased variability is expected near a transition point in a dynamical system: ongoing, internal noise perturbations cause variability in the system’s dynamics. As the system approaches a transition, its sensitivity generically increases, and the impact of the internal noise becomes more visible.
We examined within-preparation variance as a predictor of transitions by examining the membrane potential traces in their phase plane, as shown in Fig. 4 C. This allowed us to define the “mean oscillation,” by computing the mean trajectory across multiple oscillations, and a coefficient of variation (CV, SD normalized to the mean). This provides a measure of the internal variability of the oscillation from its average trajectory. We then combined these CV values (see Materials and methods) to compute an overall measure of variability (combined coefficient of variation, (CCV)) and plotted this as a function of distance to a transition in both temperature and pH-induced transitions. These CCV values are shown in Fig. 4, D–F, aligned to respective transition points (dashed red line).
We analyzed variability in preparations near temperature- and pH-induced transitions. Consistent with theoretical predictions, there was a general, statistically significant trend for the CCV to increase near a transition. Importantly, this trend is present irrespective of the type of transition or the perturbation (temperature or pH) that led to it. Nonetheless, this measure offers a poor prediction of proximity to a transition within any given preparation. For example, with measured variability in temperature perturbation, a CCV value of 6 could mean the preparation is at the transition point or more than 3° away. In the case of transition to silence due to pH perturbation, the variance in many of the preparations decreases near the transition to silence. Thus, although variability at the population level shows a robust increase near transition points, there is large interpreparation variability in this relationship that would preclude its use as a reliable predictive tool for the onset of a transition in any given preparation.
Combined effects of temperature and pH
Lastly, we sought to ask whether there were interactions between pH perturbations and temperature perturbations. We started by performing pH perturbations at 25°C, a temperature at which all preparations are bursting, and obtaining intracellular recordings of the PD neuron in the isolated oscillator (Fig. 5 A). We then subjected these same preparations to decreasing pH ramps. The transition points are highly variable across preparations; as a consequence, pH ramps performed at 11 and 25°C show transitions in overlapping ranges (Fig. 5, A and C).
To control for interpreparation variability when testing the interaction of pH and temperature, we exposed seven preparations to multiple perturbations: decreasing pH at 11°C, decreasing pH at 25°C, and increasing temperature (Fig. 5 B). This allowed us to test whether the combination of temperature and pH will make the preparations more sensitive (transition at less extreme values). We fitted a linear model to the transition point data to describe transition pH as a function of transition temperature and transition type. This analysis showed a nonsignificant interaction between transition temperature and transition pH (p = 0.658). Although the interaction between temperature and pH was not statistically significant, there is a small, positive, significant interaction (β = 0.01, p < 0.01) between temperature and tonic-to-silent transitions, suggesting that higher temperature makes the preparations slightly more robust to pH perturbation. Together, these results show that there is a modest interaction between temperature and pH perturbations that, surprisingly, confers slightly higher pH robustness at more extreme temperatures.
Stereotyped transitions during temperature and pH perturbations
We have shown that the pacemaker oscillation undergoes different types of transitions in activity patterns when exposed to extreme temperature versus pH. In Fig. 5 C, we plotted the activity patterns as a function of temperature or pH, respectively, for the set of experiments from Figs. 2 and 3. In the temperature experiments combined with those from Fig. 5 B, all 26 preparations transitioned from bursting to silence without tonic spiking. In contrast, 25 of 26 pH experiments transitioned from bursting to tonic spiking to silence, whereas the remaining one transitioned from bursting to silence.
A geometrical model of neuronal excitability captures global transitions
Despite significant quantitative variability in transitions induced by temperate and pH perturbations, our data revealed consistent qualitative changes across preparations. That is, the sequence of changes in dynamics is largely preserved even though the critical experimental parameter value at which a transition occurs may vary substantially from one animal to the next. Such qualitative consistency suggests that there is a core underlying dynamics common to each biological preparation and that the multitude of bare biophysical parameters and state equations that capture quantitative electrophysiological properties can be boiled down to a minimal set, sufficient for capturing all qualitative dynamics including bursting, tonic firing, and silence. In such a minimal model, global perturbations should appear as paths traversing well-defined boundaries between behavioral states, with the boundaries defining the order in which transitions can occur.
We therefore asked whether such a unifying model exists that can capture and shed insight on our observations. We recently proposed (22) a reduced model that captures the dynamics of neuronal excitability through a reduction to three state variables that describe dynamics on three separate timescales: fast (action potential generation), slow (action potential repolarization, interspike period, and burst generation), and ultraslow (burst termination and interburst period). This model was first introduced in (22), and a full description of its derivation can be found there. For completeness, we give an abbreviated account of how it is derived and interpreted here. The model is based on a current balance equation:
| (1a) |
| (1b) |
and
| (1c) |
where V models the membrane potential, Vs is the state variable, and Vu is the ultraslow state variable. The parameters 0 < εu ≪ εs ≪ 1 fix the characteristic time constants of the ultraslow and slow variables, respectively. The membrane potential dynamics is determined by the three current components, Ifast(V), Is(Vs), and Iu(Vu), modeling fast, slow, and ultraslow ionic current variations. The three timescales are typically characterized by identifiable ionic currents with particular time constants of activation and inactivation (see (20,21,40) for details). For example, the fast timescale includes the activation of fast (transient and persistent) sodium currents. The slow timescale includes the inactivation of transient sodium currents, the activation of delayed rectifier potassium currents, and the activation of calcium currents. The ultraslow timescales include the inactivation of calcium currents and activation of calcium-gated potassium currents. Other important currents for STG neuron dynamics are A-type potassium currents, which in the above classification have a slow activation and an ultraslow inactivation.
The functional forms of the three current components in system (1) are chosen to capture the key qualitative features of measured early ( 1 ms), late ( 10 ms), and steady-state (>100 ms) current/voltage (I/V) curves, as would be measured in step voltage clamp experiments. Such I/V curves have been extensively characterized in the pacemaker neurons that we are studying here, over many decades of research in our laboratories and elsewhere (41, 42, 43, 44, 45). The early-current component is modeled by Iearly(V) = Ifast(V), the late-current component is modeled by Ilate(V) = Iearly(V) + Is(V), and the steady-state current component is modeled by Iss(V) = Ilate(V) + Iu(V). The minimal model that respects the qualitative shape of these I/V curves is
| (2a) |
| (2b) |
and
| (2c) |
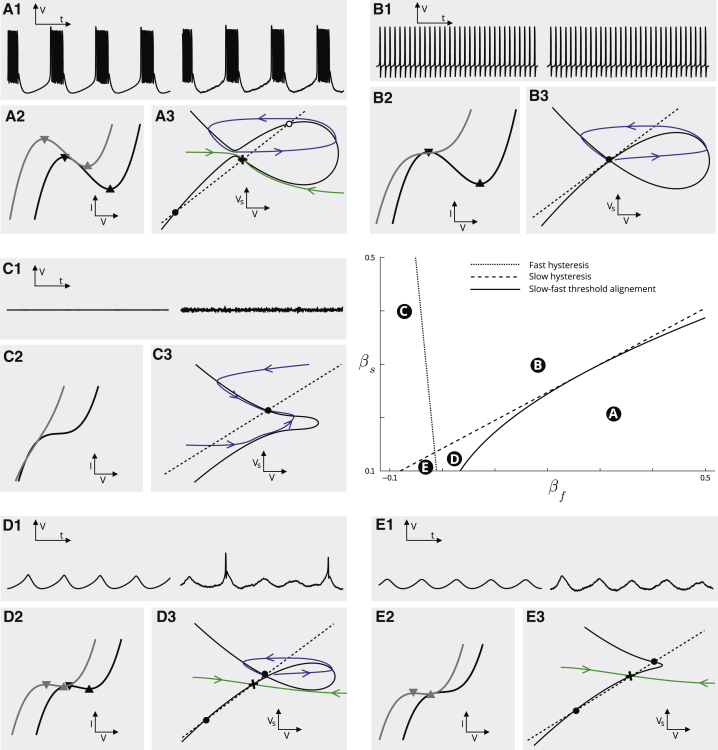
Minimal models of this kind are commonly referred to as normal forms. The specific form above is formally justified using singularity theory methods, described in detail previously (22). This earlier work also showed that this model is sufficient for capturing the excitability types observed in STG pacemaker neurons, which we demonstrate in the parameter chart in Fig. 6. The three parameters βf, βs, and γ appearing in (2a), (2b), (2c) shape the model early, late, and steady-state I/V curve with the same qualitative principle as ionic current modulation in a biophysical model. For fixed negative γ, the (βf, βs) parameter chart is partitioned into different qualitative regions, of which we only consider the five labeled A–E (the only relevant regions for this study). A similar partitioning, with slight quantitative differences, appears for positive γ.
Figure 6.
Behavioral parameter chart of the geometrical normal form model. A1–E1: electrical behavior of the geometrical model in five distinct qualitative regimes identified in the (βf, βs) parameter chart (center right panel). Left trace is deterministic. Right trace is with a small added noise used to reproduce possible spontaneous stochastic spiking as observed along temperature perturbations at the transition from periodic bursting to slow oscillatory potentials. A2–E2: geometrical model early (black) and late (gray) I/V curves in the different regimes. Thresholds (i.e., maxima and minima) of the two I/V curves are indicated by black and gray triangles, respectively. A3–E3: slow-fast (V, Vs) phase portrait of the geometrical model for frozen ultraslow (Vu) variable. The value at which the ultraslow variable was frozen was chosen to highlight the dynamical properties (bistable, excitable, globally stable, etc.) of the slow-fast subsystem, which largely determines the resulting rhythmic behavior in the presence of ultraslow adaptation (see text for details). To see this figure in color, go online.
Regions of distinct qualitative dynamics are characterized by different early (black curves in Fig. 6, A2–E2) and late (gray curves in Fig. 6, A2–E2) I/V curve configurations. The steady-state I/V curve is always monotonically increasing in the chosen parameter range and is not drawn for clarity. Changes in I/V curve configuration are reflected into changes in the model electrical behavior (Fig. 6, A1–E1; left is the deterministic simulation and right is with a small added noise) and in the underlying geometric fast-slow (V, Vs) phase portrait (Fig. 6, A3–E3). These phase portraits can be analyzed with standard dynamical system tools (46) to infer the type of bifurcations underlying excitability in the various behavioral regimes. The transitions between behavioral regimes are also ruled by bifurcations of higher codimension. For instance, a pitchfork bifurcation organizes the transition between regimes A and B (22). To maintain a clear connection with experiments and biophysical properties, in the remainder of the section, we solely focus on I/V curve shaping rather than on describing bifurcations.
In region C, both the early and late (and thus all three) I/V curves are monotonically increasing. No negative conductance interval exists in any of the three timescales, and the model exhibits a passive, nonexcitable behavior, with a unique globally asymptotically stable equilibrium.
In region B, the early I/V curve exhibits a negative conductance interval, which makes the model spike excitable and capable of periodic spiking for sufficiently large depolarizing currents. The interval of fast negative conductance is delimited by the fast low and high thresholds, i.e., the maximum and minimum of the fast I/V curve, respectively (black triangles in Fig. 6, B2). The late I/V curve is monotone in this region, which implies that the fast-slow phase portrait possesses a unique (excitable or unstable, depending on Iapp) equilibrium. The model cannot exhibit any type of slow (e.g., burst) excitability in this regime. At the dashed transition set between regions B and C, the early I/V curve has an inflection point, i.e., a fast hysteresis point in the jargon of singularity theory. In regions A, D, and E, the late I/V curve also exhibits an interval of negative conductance, and the resulting excitable types depend on the interaction between the slow and the fast negative conductance. The dashed boundary line (labeled “slow hysteresis”) corresponds to the existence of an inflection point in the slow I/V curve, i.e., a slow hysteresis that enables slow wave oscillations.
In regions A, D, and E), the slow low threshold (downward gray triangle in Fig. 6, A2–E2) is always located at more hyperpolarized potentials then the fast low threshold (downward black triangle) and thus dominates excitability. The model is slow excitable, i.e., it either produces bursts or slow oscillatory potentials in response to excitations. In region A, the high slow threshold (upward gray triangle) falls in the fast negative conductance region, which means that the slow excited state is unstable and surrounded by a spiking limit cycle, as illustrated in the associated geometric phase plane. The ultraslow dynamics turns the resulting rest-spike bistability into bursting. In region D, the slow high threshold (upward gray triangle in Fig. 6, D2) happens before the fast low threshold (downward black triangle), i.e., the slow excited state is stable but fast excitable. In the absence of noise (or any other excitatory inputs), the model produces slow oscillations, but in the presence of exogenous inputs (noise in the stochastic simulations on the right), it produces conditional spiking on top of the slow wave caused by crossing the low fast threshold.
The transition between regions A and D (solid line) corresponds to fast and slow threshold alignment. Geometrically, this alignment corresponds to a transcritical singularity (21). Crossing the fast hysteresis line between D and E, the only remaining negative conductance is the slow one and the model is in a purely slow excitable mode, i.e., it produces slow oscillations without conditional spiking on top of the slow wave.
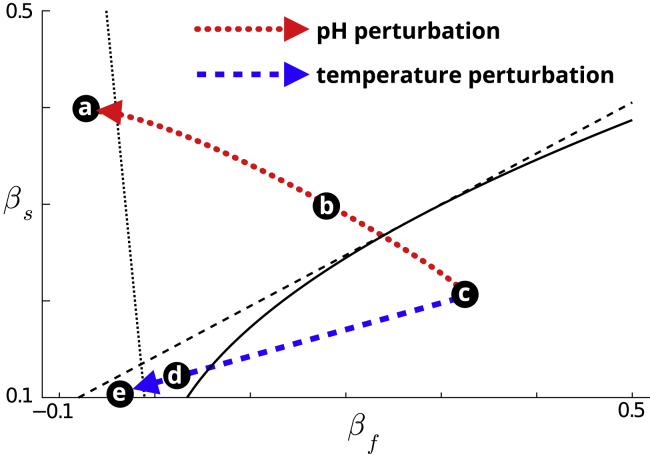
Having related the dynamical regimes of this model to experimentally observed behaviors, we can now show that the allowable transitions in the reduced parameter space of the model are predictive of the transitions seen experimentally. Importantly, these transitions are compatible with continuous paths in the reduced parameter chart that capture the two global perturbations—temperature and pH—that we subjected the preparations to.
Fig. 7 shows a projection of two continuous modulatory paths onto the same reduced parameter space as Fig. 6, center right, corresponding to modulation of the fast (βf) and slow (βs) current-voltage relations. The two paths depart from the unperturbed, bursting behavior (region A) via two transverse routes. One path (red) undergoes a transition marked by a loss of slow excitability leading to tonic spiking (regions A to B), followed by loss of fast excitability/spiking (regions B to C). This sequence of transitions is seen in pH perturbations. The other path (blue) is characterized by a relative change in slow and fast excitable thresholds, leading to slow oscillations with spontaneous/isolated spikes (regions A to D). Further movement in this direction leaves lower amplitude slow oscillations as fast excitability is removed at the transition from region D to region E. This alternative path from the same starting point corresponds to the qualitative transitions seen in temperature perturbations.
Figure 7.
Temperature and pH perturbation as qualitative geometric paths. The behavioral transitions observed in response to increasing pH and temperature perturbations emerge as transverse paths in the geometrical model’s reduced parameter space. To see this figure in color, go online.
These two distinct paths correspond to transverse movements in the reduced parameter space and, strikingly, capture completely the qualitative transitions observed in experiments. It is important to remark that the transition lines between distinct behavioral regimes in the reduced parameter space map smoothly to (formally, are embedded into) hypersurfaces in the high-dimensional biophysical parameter space. Similarly, the reduced pH and temperature perturbation paths map to a whole family of paths in the high-dimensional biophysical parameter space. This observation explains how the large quantitative variability observed in experiments is compatible with consistent qualitative physiological behavior of this circuit across animals and preparations. Taken together, our results suggest a parsimonious, universal model of excitability that describes the core dynamics in this neuronal oscillator.
Discussion
Many biological oscillators, such as those found in the heart and nervous system, depend on the orderly activation and inactivation of many voltage- and time-dependent currents (47, 48, 49, 50, 51). Because the temperature and pH dependencies of each ion channel are different, this poses an immediate problem for finding solutions that are robust against these perturbations (15). Indeed, random searches of parameter regimes demonstrate that oscillator models that are resilient to large changes in temperature are difficult to find (8,9,14). Compounding this problem is that in the STG, stable behavior of the full pyloric rhythm and its central oscillator are remarkably robust to temperature and pH changes (12,33). This is despite the fact that each cell and circuit conductance vary across animal by ∼2- to 6-fold (4,5,16, 17, 18,52, 53, 54, 55, 56).
This suggests that despite animal-to-animal variability, the circuit has found parameters that allow detuning of ionic currents and synaptic properties to occur but nonetheless ensure a stable rhythmic output. The oscillators studied here, although variable across preparations, are resilient over a wide range of temperature. Moreover, for the oscillator to remain robust to temperature and pH perturbations that cause parameters to change significantly, it is clear that the biological mechanisms that tune circuit properties do so in a way that ensures specific functional organization between physiological parameters amid a large degree of variability (15).
Consistent with underlying parameter variability, we find that pH and temperature cause the oscillator to fail at critical values of temperature and pH that vary significantly across animals. Importantly, the modes of failure correspond to reversible transitions to distinct activity regimes, from bursting to tonic spiking and then silence in the case of a pH ramp and from bursting to silence in the case of a temperature ramp. In agreement with general theory of critical transitions in dynamical systems, we detect an increase in the intrinsic variability of the oscillator close to the critical point at which the oscillation fails (35,36,38,39). The consistency of these qualitative transitions between preparations is strong evidence that the pyloric oscillator operates with a consistent type of oscillatory dynamics. Together, these findings show that although large variability is indeed present in the physiological properties of the STG, the mechanisms that organize physiological parameters place the oscillator in a highly robust regime with consistent qualitative behavior. This suggests that the oscillator achieves the same qualitative type of oscillation despite large variability in underlying physiological variables.
Despite the surprising robustness we have characterized in this circuit, there is clear evidence of underlying parameter variability. Although most preparations undergo the same transitions between different activity patterns as pH and temperature are varied, the precise values at which these transitions occur is variable. On the other hand, the transitions between different activity patterns were remarkably reliable; temperature elevation consistently resulted in a transition from bursting to silence, whereas in most preparations, a decrease in pH resulted in a sequence of transitions from bursting to tonic spiking, then from tonic spiking to silence. Together, these findings illustrate that collective ensemble properties can be highly consistent, even if quantitative, low-level parameters are not. A plausible explanation for how such consistency arises is that cellular components such as ion channels are regulated in a collective, modular fashion, with multiple channel types coregulated by the same molecular pathway (15,18,55,57).
We provided a general geometrical model of excitability that explains the consistency of qualitative changes induced by temperature and pH perturbations across animals and preparations. The defining equations of our model are simple cubic polynomials and thus independent of specific biophysical details. Despite their simplicity, they were derived via singularity theory methods that provably capture all the possible qualitative reshaping of neuronal I/V curves at different timescales, as induced by perturbations or modulations (22). The presence of temperature- and pH-like perturbation paths in the reduced parameter space of the model is therefore consistent with a general, qualitative oscillator dynamics that is independent of specific quantitative properties of different animals and preparations, such as maximal conductance density or Q10s. Conversely, the measured variability in those biophysical properties is exactly what drives quantitative variability in the perturbation critical points across animals and preparations without clashing with the existence of such a general qualitative mechanism.
More classical reduced modeling approaches to perturbation and modulation (13,21,40,50) usually work by selecting a specific subset of biophysical properties of interest, implementing them in a heuristically simplified computational model, and performing a bifurcation analysis of the resulting equations. The model specificity of such an approach is useful to address specific questions (e.g., the role of Q10s in shaping response variability to perturbations) but can fall short in proving the existence of general mechanisms shared across animals and preparations that are independent of variable and largely unknown biophysical details.
What general lessons can we learn from this work? We can view the pyloric oscillator preparation as a vastly simplified biological model of a nervous system that is subject to particular failure modes. Other, more complex nervous systems such as the brains of vertebrate species exhibit many more components and kinds of behavior, but they also show stereotyped failure modes such as seizures. Our findings illustrate just how difficult it is to predict the onset of failure, even with what might be considered ideal biological replicates of the same system. We found that at the population level, increases in oscillatory variance were indicative of the proximity to a transition out of the rhythm. This is consistent with recent theory (36,38,39) and experimental attempts to predict catastrophic events in complex natural systems (35). However, in our data, the trend in variance is far from predictive at the individual level, a problem amplified by biological variability and differential susceptibility near distinct transitions.
Our main motivation for studying combined global perturbations to a neural circuit was to assess whether robustness to one kind of perturbation implied sensitivity to other kinds of perturbations. For pH and temperature perturbations in the STG oscillator, we find a surprisingly modest interaction in the robustness of the pacemaker rhythm. This suggests that the circuit may have evolved to exhibit tolerance to both (and likely other) external insults. This combined tolerance places additional constraints on the expression and regulation of the underlying membrane currents and synaptic connections (15) and may even favor specific kinds of circuit architectures over others.
We found that the pyloric pacemaker circuit is remarkably robust to acute pH variations. This robustness is somewhat dependent on temperature, indicating that both kinds of robustness impose constraints on channel expression. However, the interaction between robustness to temperature and pH robustness was surprisingly small, consistent with recent work on the entire pyloric circuit (D. Hampton and E.M., unpublished data). This implies that the pyloric circuit and its governing oscillator occupy a region of physiological parameter space that allows temperature and pH robustness be satisfied without a severe tradeoff, as well as allowing large internal variability in ionic current expression. In line with existing hypotheses (57), we suggest that such robustness to variability and global perturbations explains the tremendous diversity of ionic currents observed in even relatively simple circuits, including the core oscillator we studied here.
Author contributions
T.O.L. conceived the study. J.R., E.M., and T.O.L. designed research. J.R. performed experiments. A.F. developed model. J.R., A.F., and T.O.L. analyzed and interpreted results. J.R. and T.O.L. wrote manuscript. J.R., A.F., E.M., and T.O.L. revised and edited manuscript.
Acknowledgments
We acknowledge Anatoly Rinberg for his contribution to this work in performing experiments that were preliminary to the study here. We also thank Jessica Haley for sharing experimental results that informed the design of these experiments.
This work is funded by NIH Grants R35 NS 097343 and MH 46742 to E.M. and by ERC Grant StG 2016 716643 FLEXNEURO to T.O.L.
Editor: Stanislav Shvartsman.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.01.038.
Contributor Information
Eve Marder, Email: marder@brandeis.edu.
Timothy O’Leary, Email: timothy.oleary@eng.cam.ac.uk.
Supporting material
References
- 1.Obara M., Szeliga M., Albrecht J. Regulation of pH in the mammalian central nervous system under normal and pathological conditions: facts and hypotheses. Neurochem. Int. 2008;52:905–919. doi: 10.1016/j.neuint.2007.10.015. [DOI] [PubMed] [Google Scholar]
- 2.Marder E., Haddad S.A., Kispersky T. How can motor systems retain performance over a wide temperature range? Lessons from the crustacean stomatogastric nervous system. J. Comp. Physiol. A Neuroethol. Sens. Neural Behav. Physiol. 2015;201:851–856. doi: 10.1007/s00359-014-0975-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pequeux A. Osmotic regulation in crustaceans. J. Crustac. Biol. 1995;15:1–60. [Google Scholar]
- 4.Robertson R.M., Money T.G. Temperature and neuronal circuit function: compensation, tuning and tolerance. Curr. Opin. Neurobiol. 2012;22:724–734. doi: 10.1016/j.conb.2012.01.008. [DOI] [PubMed] [Google Scholar]
- 5.Haddad S.A., Marder E. Circuit robustness to temperature perturbation is altered by neuromodulators. Neuron. 2018;100:609–623.e3. doi: 10.1016/j.neuron.2018.08.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Garrity P.A., Goodman M.B., Sengupta P. Running hot and cold: behavioral strategies, neural circuits, and the molecular machinery for thermotaxis in C. elegans and Drosophila. Genes Dev. 2010;24:2365–2382. doi: 10.1101/gad.1953710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sengupta P., Garrity P. Sensing temperature. Curr. Biol. 2013;23:R304–R307. doi: 10.1016/j.cub.2013.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Alonso L.M., Marder E. Temperature compensation in a small rhythmic circuit. eLife. 2020;9:e55470. doi: 10.7554/eLife.55470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Roemschied F.A., Eberhard M.J., Schreiber S. Cell-intrinsic mechanisms of temperature compensation in a grasshopper sensory receptor neuron. eLife. 2014;3:e02078. doi: 10.7554/eLife.02078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tang L.S., Taylor A.L., Marder E. Robustness of a rhythmic circuit to short- and long-term temperature changes. J. Neurosci. 2012;32:10075–10085. doi: 10.1523/JNEUROSCI.1443-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tang L.S., Goeritz M.L., Marder E. Precise temperature compensation of phase in a rhythmic motor pattern. PLoS Biol. 2010;8:e1000469. doi: 10.1371/journal.pbio.1000469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Soofi W., Goeritz M.L., Stein W. Phase maintenance in a rhythmic motor pattern during temperature changes in vivo. J. Neurophysiol. 2014;111:2603–2613. doi: 10.1152/jn.00906.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rinberg A., Taylor A.L., Marder E. The effects of temperature on the stability of a neuronal oscillator. PLoS Comput. Biol. 2013;9:e1002857. doi: 10.1371/journal.pcbi.1002857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Caplan J.S., Williams A.H., Marder E. Many parameter sets in a multicompartment model oscillator are robust to temperature perturbations. J. Neurosci. 2014;34:4963–4975. doi: 10.1523/JNEUROSCI.0280-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.O’Leary T., Marder E. Temperature-robust neural function from activity-dependent ion channel regulation. Curr. Biol. 2016;26:2935–2941. doi: 10.1016/j.cub.2016.08.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Schulz D.J., Goaillard J.M., Marder E.E. Quantitative expression profiling of identified neurons reveals cell-specific constraints on highly variable levels of gene expression. Proc. Natl. Acad. Sci. USA. 2007;104:13187–13191. doi: 10.1073/pnas.0705827104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schulz D.J., Goaillard J.M., Marder E. Variable channel expression in identified single and electrically coupled neurons in different animals. Nat. Neurosci. 2006;9:356–362. doi: 10.1038/nn1639. [DOI] [PubMed] [Google Scholar]
- 18.Temporal S., Lett K.M., Schulz D.J. Activity-dependent feedback regulates correlated ion channel mRNA levels in single identified motor neurons. Curr. Biol. 2014;24:1899–1904. doi: 10.1016/j.cub.2014.06.067. [DOI] [PubMed] [Google Scholar]
- 19.Shruti S., Schulz D.J., Marder E. Electrical coupling and innexin expression in the stomatogastric ganglion of the crab Cancer borealis. J. Neurophysiol. 2014;112:2946–2958. doi: 10.1152/jn.00536.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Drion G., Franci A., Dethier J., Sepulchre R. Dynamic input conductances shape neuronal spiking. eNeuro. 2015;2 doi: 10.1523/ENEURO.0031-14.2015. ENEURO.0031-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Franci A., Drion G., Sepulchre R. A balance equation determines a switch in neuronal excitability. PLoS Comput. Biol. 2013;9:e1003040. doi: 10.1371/journal.pcbi.1003040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Franci A., Drion G., Sepulchre R. Modeling the modulation of neuronal bursting: a singularity theory approach. SIAM J. Appl. Dyn. Syst. 2014;13:798–829. [Google Scholar]
- 23.Tombaugh G.C., Somjen G.G. Effects of extracellular pH on voltage-gated Na+, K+ and Ca2+ currents in isolated rat CA1 neurons. J. Physiol. 1996;493:719–732. doi: 10.1113/jphysiol.1996.sp021417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Church J., Baxter K.A., McLarnon J.G. pH modulation of Ca2+ responses and a Ca2+-dependent K+ channel in cultured rat hippocampal neurones. J. Physiol. 1998;511:119–132. doi: 10.1111/j.1469-7793.1998.119bi.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Xiong Z.-Q., Stringer J.L. Extracellular pH responses in CA1 and the dentate gyrus during electrical stimulation, seizure discharges, and spreading depression. J. Neurophysiol. 2000;83:3519–3524. doi: 10.1152/jn.2000.83.6.3519. [DOI] [PubMed] [Google Scholar]
- 26.Cook D.L., Ikeuchi M., Fujimoto W.Y. Lowering of pHi inhibits Ca2+-activated K+ channels in pancreatic B-cells. Nature. 1984;311:269–271. doi: 10.1038/311269a0. [DOI] [PubMed] [Google Scholar]
- 27.Hille B. Third Edition. Sinauer Associates; Sunderland, MA: 2001. Ion Channels of Excitable Membranes. [Google Scholar]
- 28.Golowasch J., Deitmer J.W. pH regulation in the stomatogastric ganglion of the crab Cancer pagurus. J. Comp. Physiol. A. 1993;172:573–581. [Google Scholar]
- 29.Truchot J.P. Temperature and acid-base regulation in the shore crab Carcinus maenas (L.) Respir. Physiol. 1973;17:11–20. doi: 10.1016/0034-5687(73)90106-0. [DOI] [PubMed] [Google Scholar]
- 30.Sartoris F.-J., Pörtner H.-O. Temperature dependence of ionic and acid-base regulation in boreal and arctic Crangon crangon and Pandalus borealis. J. Exp. Mar. Biol. Ecol. 1997;211:69–83. [Google Scholar]
- 31.Whiteley N. Physiological and ecological responses of crustaceans to ocean acidification. Mar. Ecol. Prog. Ser. 2011;430:257–271. [Google Scholar]
- 32.Marder E., Eisen J.S. Transmitter identification of pyloric neurons: electrically coupled neurons use different transmitters. J. Neurophysiol. 1984;51:1345–1361. doi: 10.1152/jn.1984.51.6.1345. [DOI] [PubMed] [Google Scholar]
- 33.Haley J.A., Hampton D., Marder E. Two central pattern generators from the crab, Cancer borealis, respond robustly and differentially to extreme extracellular pH. eLife. 2018;7:e41877. doi: 10.7554/eLife.41877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Doering C.J., McRory J.E. Effects of extracellular pH on neuronal calcium channel activation. Neuroscience. 2007;146:1032–1043. doi: 10.1016/j.neuroscience.2007.02.049. [DOI] [PubMed] [Google Scholar]
- 35.Veraart A.J., Faassen E.J., Scheffer M. Recovery rates reflect distance to a tipping point in a living system. Nature. 2011;481:357–359. doi: 10.1038/nature10723. [DOI] [PubMed] [Google Scholar]
- 36.Scheffer M., Carpenter S.R., Vandermeer J. Anticipating critical transitions. Science. 2012;338:344–348. doi: 10.1126/science.1225244. [DOI] [PubMed] [Google Scholar]
- 37.Kandel D., Domany E., Loh E., Jr. Simulations without critical slowing down. Phys. Rev. Lett. 1988;60:1591–1594. doi: 10.1103/PhysRevLett.60.1591. [DOI] [PubMed] [Google Scholar]
- 38.Scheffer M. Complex systems: foreseeing tipping points. Nature. 2010;467:411–412. doi: 10.1038/467411a. [DOI] [PubMed] [Google Scholar]
- 39.Chisholm R.A., Filotas E. Critical slowing down as an indicator of transitions in two-species models. J. Theor. Biol. 2009;257:142–149. doi: 10.1016/j.jtbi.2008.11.008. [DOI] [PubMed] [Google Scholar]
- 40.Drion G., O’Leary T., Marder E. Ion channel degeneracy enables robust and tunable neuronal firing rates. Proc. Natl. Acad. Sci. USA. 2015;112:E5361–E5370. doi: 10.1073/pnas.1516400112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Golowasch J., Bose A., Nadim F. A balance of outward and linear inward ionic currents is required for generation of slow-wave oscillations. J. Neurophysiol. 2017;118:1092–1104. doi: 10.1152/jn.00240.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gray M., Golowasch J. Voltage dependence of a neuromodulator-activated ionic current. eNeuro. 2016;3 doi: 10.1523/ENEURO.0038-16.2016. ENEURO.0038-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Rodriguez J.C., Blitz D.M., Nusbaum M.P. Convergent rhythm generation from divergent cellular mechanisms. J. Neurosci. 2013;33:18047–18064. doi: 10.1523/JNEUROSCI.3217-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Golowasch J., Marder E. Proctolin activates an inward current whose voltage dependence is modified by extracellular Ca2+ J. Neurosci. 1992;12:810–817. doi: 10.1523/JNEUROSCI.12-03-00810.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Golowasch J., Marder E. Ionic currents of the lateral pyloric neuron of the stomatogastric ganglion of the crab. J. Neurophysiol. 1992;67:318–331. doi: 10.1152/jn.1992.67.2.318. [DOI] [PubMed] [Google Scholar]
- 46.Guckenheimer J., Holmes P. Springer Science and Business Media; New York: 2013. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. [Google Scholar]
- 47.Sobie E.A. Parameter sensitivity analysis in electrophysiological models using multivariable regression. Biophys. J. 2009;96:1264–1274. doi: 10.1016/j.bpj.2008.10.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tobin A.E., Calabrese R.L. Endogenous and half-center bursting in morphologically inspired models of leech heart interneurons. J. Neurophysiol. 2006;96:2089–2106. doi: 10.1152/jn.00025.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Canavier C.C., Clark J.W., Byrne J.H. Simulation of the bursting activity of neuron R15 in Aplysia: role of ionic currents, calcium balance, and modulatory transmitters. J. Neurophysiol. 1991;66:2107–2124. doi: 10.1152/jn.1991.66.6.2107. [DOI] [PubMed] [Google Scholar]
- 50.Guckenheimer J., Gueron S., Harris-Warrick R.M. Mapping the dynamics of a bursting neuron. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1993;341:345–359. doi: 10.1098/rstb.1993.0121. [DOI] [PubMed] [Google Scholar]
- 51.Alonso L.M., Marder E. Visualization of currents in neural models with similar behavior and different conductance densities. eLife. 2019;8:e42722. doi: 10.7554/eLife.42722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Goaillard J.-M., Taylor A.L., Marder E. Functional consequences of animal-to-animal variation in circuit parameters. Nat. Neurosci. 2009;12:1424–1430. doi: 10.1038/nn.2404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Grashow R., Brookings T., Marder E. Compensation for variable intrinsic neuronal excitability by circuit-synaptic interactions. J. Neurosci. 2010;30:9145–9156. doi: 10.1523/JNEUROSCI.0980-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Taylor A.L., Goaillard J.M., Marder E. How multiple conductances determine electrophysiological properties in a multicompartment model. J. Neurosci. 2009;29:5573–5586. doi: 10.1523/JNEUROSCI.4438-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.O’Leary T., Williams A.H., Marder E. Cell types, network homeostasis, and pathological compensation from a biologically plausible ion channel expression model. Neuron. 2014;82:809–821. doi: 10.1016/j.neuron.2014.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.O’Leary T., Williams A.H., Marder E. Correlations in ion channel expression emerge from homeostatic tuning rules. Proc. Natl. Acad. Sci. USA. 2013;110:E2645–E2654. doi: 10.1073/pnas.1309966110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.O’Leary T. Homeostasis, failure of homeostasis and degenerate ion channel regulation. Curr. Opin. Physiol. 2018;2:129–138. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.