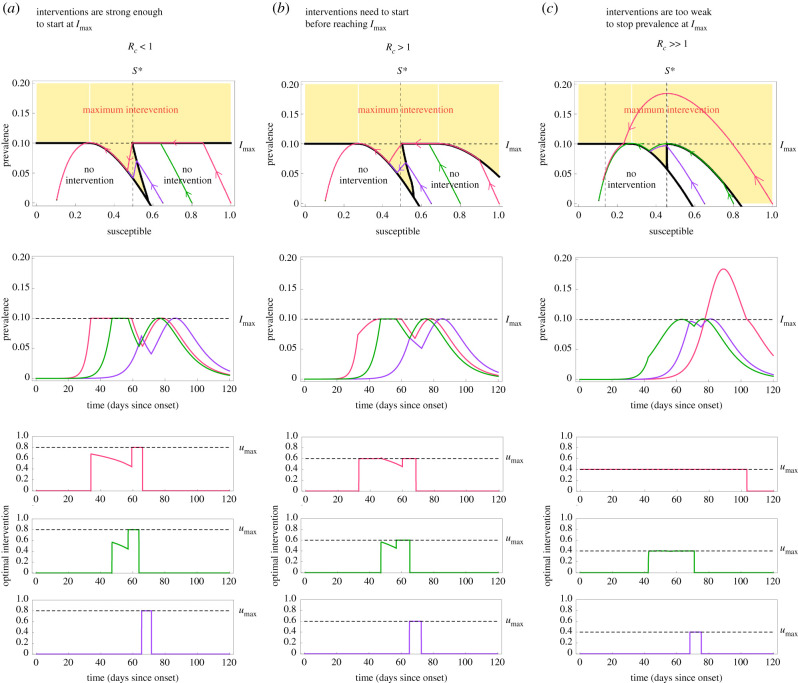
Figure 3.

Optimal non-pharmaceutical interventions in the Susceptible–Infected–Removed model. For all panels, the parameters of the SIR model are γ = 1/7, β = 0.52 (i.e. R₀ = 3.64) and I_max = 0.1. We consider a population of N = 8.855 × 10⁶ individuals (like in Mexico City) and I₀ = 1/N. Panels shows trajectories for three initial proportions of the susceptible population: large S₀ = 1 − I₀ ≈ 1 (pink), medium S₀ = 0.8 (green) and small S₀ = 0.65 (purple). (a) For u_max = 0.8, we have R_c = (1 − u_max)R₀ = 0.728 ≤ 1. In this case, the optimal intervention starts when the disease prevalence reaches I_max. Afterwards, the intervention decreases in a hyperbolic arc until reaching the point S = S*. At that time, the intervention becomes maximum in the ‘final push’ to reach the safe zone. (b) For u_max = 0.58, the controlled reproduction number is R_c = (1 − u_max)R₀ = 1.52 > 1. Here, ${\mathit{\Phi }}_{R_c}(1)>0$, implying that the epidemic still can be mitigated for initial states with S₀ ≈ 1 and I₀ ≈ 0 (pink trajectory). In this case, the optimal intervention starts when the initial condition hits the separating curve below I_max at t = 35. At that instant, the intervention starts with the maximum value u_max, and continues in that form until the trajectory reaches I_max. (c) Choosing u_max = 0.4 yields R_c = 2.184 > 1. In this case, the optimal intervention problem does not have a solution for all initial states S₀ > 0.85. This is illustrated by pink trajectory: even when applying the maximum intervention from the start, I(t) will grow beyond I_max.