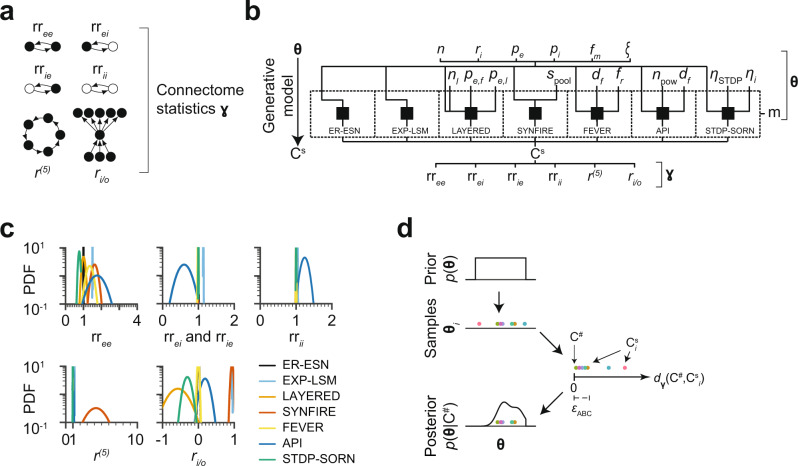
Fig. 3. Connectome statistics and generative models for approximate Bayesian inference.

a Connectome statistics $\mathit{\gamma }$ used for model distinction: relative excitatory-excitatory reciprocity ${\mathrm{rr}}_{ee}$, relative excitatory-inhibitory reciprocity ${\mathrm{rr}}_{ei}$, relative inhibitory-excitatory reciprocity ${\mathrm{rr}}_{ie}$, relative inhibitory-inhibitory reciprocity ${\mathrm{rr}}_{ii}$, relative cycles of length 5, $r^{\left(5\right)}$, and in-out degree correlation of excitatory neurons $r_{i/o}.$ b Generative model for Bayesian inference: shared set of parameters (top: number of neurons $n$, fraction of inhibitory neurons $r_i$, excitatory connectivity $p_e$, inhibitory connectivity $p_i$, fractional connectome measurement $f_m$, noise $\xi$) and model-specific parameters (middle: model choice $m$, number of layers $n_l$, excitatory forward connectivity $p_{e,f}$, excitatory lateral connectivity $p_{e,l}$, pool size $s_{\mathrm{pool}}$, STDP learning rate ${\eta }_{\mathrm{STDP}}$, intrinsic learning rate ${\eta }_i$, feature space dimension $d_f$, feverization ratio $f_r$, selectivity $n_{\mathrm{pow}}$, see Supplementary Fig. 4), generated sampled connectome C^s described by the summary statistics $\mathit{\gamma }=\left({\mathrm{rr}}_{ee},{\mathrm{rr}}_{ei},{\mathrm{rr}}_{ie},{\mathrm{rr}}_{ii},r^{\left(5\right)},r_{i/o}\right)$. c Gaussian fits of probability density functions (PDFs) of the connectome statistics $\mathit{\gamma }$ (a) for all models (see Fig. 1b). d Sketch of ABC-SMC procedure: given a measured connectome ${\mathrm{C}}^{\mathrm{\#}}$, parameters ${\mathit{\theta }}_i$ (colored dots) are sampled from the prior $p\left(\mathit{\theta }\right)$. Each ${\mathit{\theta }}_i$ generates a connectome ${\mathrm{C}}_i^{\mathrm{s}}$ that has a certain distance $d_{\mathit{\gamma }}\left({\mathrm{C}}^{\mathrm{\#}},{\mathrm{C}}_i^{\mathrm{s}}\right)$ to ${\mathrm{C}}^{\mathrm{\#}}$ in the space defined by the connectome statistics $\mathit{\gamma }$ (a). If this distance is below a threshold ${ϵ}_{\mathrm{ABC}}$, the associated parameters ${\mathit{\theta }}_i$ are added as mass to the posterior distribution $p\left(\mathit{\theta }\mid {\mathrm{C}}^{\mathrm{\#}}\right)$, and are rejected otherwise.