CLoNe: automated clustering based on local density neighborhoods for application to biomolecular structural ensembles

Abstract

Motivation

Proteins are intrinsically dynamic entities. Flexibility sampling methods, such as molecular dynamics or those arising from integrative modeling strategies, are now commonplace and enable the study of molecular conformational landscapes in many contexts. Resulting structural ensembles increase in size as technological and algorithmic advancements take place, making their analysis increasingly demanding. In this regard, cluster analysis remains a go-to approach for their classification. However, many state-of-the-art algorithms are restricted to specific cluster properties. Combined with tedious parameter fine-tuning, cluster analysis of protein structural ensembles suffers from the lack of a generally applicable and easy to use clustering scheme.

Results

We present CLoNe, an original Python-based clustering scheme that builds on the Density Peaks algorithm of Rodriguez and Laio. CLoNe relies on a probabilistic analysis of local density distributions derived from nearest neighbors to find relevant clusters regardless of cluster shape, size, distribution and amount. We show its capabilities on many toy datasets with properties otherwise dividing state-of-the-art approaches and improves on the original algorithm in key aspects. Applied to structural ensembles, CLoNe was able to extract meaningful conformations from membrane binding events and ligand-binding pocket opening as well as identify dominant dimerization motifs or inter-domain organization. CLoNe additionally saves clusters as individual trajectories for further analysis and provides scripts for automated use with molecular visualization software.

Availability and implementation

www.epfl.ch/labs/lbm/resources, github.com/LBM-EPFL/CLoNe.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The perception of molecular structures, especially proteins, is gradually shifting from the concept of one single and rigid structure to the idea that biomolecules natively exhibit a continuum of states (Frank, 2018). Protein folding, post-translational modifications (Audagnotto and Dal Peraro, 2017), binding to other molecules or their involvement in catalytic events result in vast and complex conformational landscapes. Molecular dynamics (MD), thanks to progress in both its technological and algorithmic aspects, allows for the simulation of key biomolecular events. Their observability, however, tends to be limited by currently accessible timescales. Researchers consistently come up with innovative protocols to push this limit further (Barducci et al., 2011; Bussi, 2014; Chavent et al., 2016; Doerr et al., 2016; Hamelberg et al., 2004; Noé et al., 2019; Shirts and Pande, 2000; Sultan et al., 2018; Wassenaar et al., 2015) granting us with the ability to capture protein folding as well as protein–protein, protein–membrane and protein–ligand interactions (Audagnotto et al., 2016; De Vivo et al., 2016; McKiernan et al., 2017; Oleinikovas et al., 2016). State-of-the-art protocols for small-molecule docking (Amaro et al., 2018; Kokh et al., 2011; Vahl Quevedo et al., 2014), protein–protein docking and integrative modeling strategies, in general, have shifted toward the integration of dynamics in some form as well (Abriata and Dal Peraro, 2020; Malhotra et al., 2019; Tamò et al., 2015). All of the aforementioned aspects advocate dynamics as a cornerstone of modern structural biology and push the need for efficient tools to extract functional insight from structural ensembles in general.

However, these advances come at a price. The sheer size, the intrinsic complexity and redundancy of structural ensembles makes their successful analysis and computational integration non-trivial. Coarse-graining tools such as cluster analysis effectively reduce simulations of thousands of conformations to few key biological states and hence constitute a go-to approach with countless applications to date [(Cheng et al., 2008; De Paris et al., 2015; de Souza et al., 2017), reviewed in (Peng et al., 2018; Shao et al., 2007)]. Such states may serve as basis of Markov state models (Husic and Pande, 2018; Wang et al., 2018). To our knowledge, however, an algorithm able to cluster data efficiently irrespective of their properties is still missing. Indeed, different cluster shapes, sizes and densities usually dictate which clustering approach is best suited for a given task. The most known and widely used scheme is probably that of k-means and its many variations (Jain, 2010). This center-based clustering scheme, however, suffers from unequal results due to random initializations, the a priori setting of the number of clusters and its limitation to spherical clusters. Alternatively, hierarchical schemes such as the Ward-linkage agglomerative algorithm (Ward, 1963) do not require pre-setting the number of clusters and are popular for building Markov state models (Beauchamp et al., 2012; Husic and Pande, 2017; Paris et al., 2015). They are however sensitive to noise and outliers and may suffer from non-spherical clusters (Peng et al., 2018). Conversely, DBSCAN (Ester et al., 1996) is able to manage clusters regardless of shape by utilizing density differences between clusters and noise. However, setting its parameter is not trivial and its optimal value may not be unique throughout the dataset when clusters of largely different densities are present. This limitation is at the core of OPTICS, which can be seen as an extension of DBSCAN (Ankerst et al., 1999), although not strictly advertised as a clustering algorithm.

Defining metastable states of proteins is non-trivial due to the large and often redundant number of internal degrees of freedom, yielding sampled conformational spaces with local minima often devoid of biological significance. We can make the assumption that, given enough sampling and a choice of relevant features, metastable states would lie in regions or clusters of high density, which would be separated by valleys of different density levels that would correspond to transitional states. Furthermore, no assumption can be made on the shape or relative densities of clusters, which would depend on both conformational sampling and target system. Rodriguez and Laio (2014) designed the Density Peaks (DP) algorithm aimed at clustering regardless of shape and dimensionality. Their algorithm generated significant interest thanks to their clever definition of cluster centers, which states that a cluster center should display a higher density (ρ) than its neighbors and a high distance to another point of higher density (δ). DP takes a single input parameter, which relates to a cutoff distance for the computation of ρ. However, it requires the user to specify thresholds for both ρ and δ mid-computation in order to select the cluster centers, which prevents a fully automated clustering process. DP has since been improved by the inclusion of k nearest neighbors (kNN) (Du et al., 2016; Xie et al., 2016; Zhang and Li, 2015) or heat diffusion (Mehmood et al., 2016) for a more robust estimation of ρ, which allows for a better handling of cases where clusters have significantly different densities. These improvements still require user intervention for selecting cluster centers. Conversely, Wang and Xu (2017) built on DP to automatically select cluster centers based on maximizing an average silhouette index, although other input parameters are required instead. Liang and Cheng coupled principles from DBSCAN with a divide-and-conquer approach to recursively and automatically select cluster centers (Liang and Chen, 2016). Recently, d’Errico et al. coupled DP with a non-parametric density estimator (Rodriguez et al., 2018), yielding Density Peaks Advanced (DPA; d’Errico et al., 2018). While exhibiting impressive robustness to a variety of cluster shapes, densities and to outliers, DPA still suffers from a few issues. We found that it performed worse than the original on some typical benchmark datasets, and requires a sensitive albeit unique input parameter. Moreover, both DP and DPA exhibit an inconsistent outlier removal procedure. These drawbacks may prove crucial when targeting structural biological data, where regions at lower effective density may have equal or even increased significance than others at higher densities. The complexity of biological structures leads to numerous unique yet equally relevant choices of features, each with their own topology. The analysis of such datasets is greatly hindered by sensitivity to input parameters, which implies that tedious fine-tuning steps have to be undertaken.

Here, we introduce an approach to remedy these drawbacks, enabling a facilitated analysis of complex real-world datasets from structural biology. Our approach builds on the original DP algorithm by introducing a fragmenting of the data into specific density distributions. In essence, the local densities of each point are computed using nearest neighbors and a Gaussian kernel and points associated with local density maxima are identified as putative cluster centers. To increase robustness to non-spherical cluster shapes, clusters are merged using the Bhattacaryaa coefficient (Bhattacharyya, 1943) by comparing density distributions derived from putative cluster cores and boundaries. Finally, outliers from impromptu noise fluctuations are removed by means of a Bayes classifier. This, to the best of our knowledge, constitute an original contribution to the density peaks algorithm. Termed Clustering based on Local density Neighborhoods (CLoNe), our approach relies on a single input parameter that is both robust and intuitive to set. We test it on many typical benchmark datasets and against state-of-the-art clustering schemes. The local focus of CLoNe allows for the detection of biological states of smaller frequency while its ease of use allows the researcher to focus on choosing relevant biological features for pre-processing or analyzing their structural ensemble without being hindered by algorithmic limitations. Furthermore, CLoNe outputs useful molecular visualization scripts for the validation of cluster relevance in the target biological context (Supplementary Fig. S1). We apply CLoNe on a range of structural datasets from MD simulations or integrative modeling studies, each time detailing the feature selection process and which information can be extracted from the results. Our examples cover previously published studies on protein–membrane interactions, internal structural rearrangements of disordered proteins, cryptic allosteric pocket formation and transmembrane dimerization motifs, and highlight the broad advantages of CLoNe for the analysis of molecular structural ensembles.

2 Materials and methods

An overview and basic usage of CLoNe is available in Supplementary Figure S1, on GitHub and the webpage of our laboratory (see Abstract section). We created a synthetic dataset containing clusters of significantly different densities and various shapes in order to showcase the procedure behind our approach. CLoNe starts by finding the k nearest neighbors of each point in a dataset X of N points using k-nearest neighbors (kNN) (Pedregosa et al., 2011), yielding a neighbor matrix M where each row i contains all the neighbors j of point i in increasing order of Euclidean distance. To account for significant density differences between clusters, we initially assume that all points are cluster centers. In a first step, we estimate the local density ρ of each point i using a Gaussian kernel:

$${\rho }_i=\sum _{jϵ{\mathit{kNN}}_i}{e}^{{-\left(\frac{M_{i,j}}{d_c}\right)}^2}=\sum _{jϵ{\mathit{kNN}}_i}{\rho }_{ij}$$ (1)

where kNN_i is the set of nearest neighbors of i in increasing order of distance and d_c is a cutoff distance defined as to be superior to a user-defined percentage p_dc (the single input parameter of CLoNe) of all distances within M, similar to the original DP algorithm (Rodriguez and Laio, 2014). We define the core of putative cluster i as the set of neighbors that contribute to ρ_i at least as much of the j−1 previous neighbors on average:

$${\mathit{core}}_i=\left\{j\mathrm{ }ϵ\mathrm{ }{\mathit{kNN}}_i|{\rho }_{ij}\ge \frac{1}{p_{dc}N}{\sum }_{k=0}^{j-1}{\rho }_{ik}\right\}$$ (2)

We show in Figure 1a the cardinality (number of elements) of the core of each point in our synthetic dataset. As expected, this number is higher for points closer to real cluster centers and lower for points laying on the outskirt of clusters. The visualization of core cardinalities is an efficient way to observe the underlying topology of the dataset. In order to identify if i is a genuine candidate for cluster center, we identify its first neighbor j of higher density. If neighbor j belongs to core_i, then neighbor j is a better candidate for cluster center in this region than i. Conversely, i is a genuine candidate for cluster center if j is not in the core of i. Cluster assignation is done in a single step by assigning a point to the same cluster as its nearest point of higher density, in order of decreasing local density, similar to the original DP approach. The results at this stage of CLoNe are shown in Figure 1a.

Fig. 1.

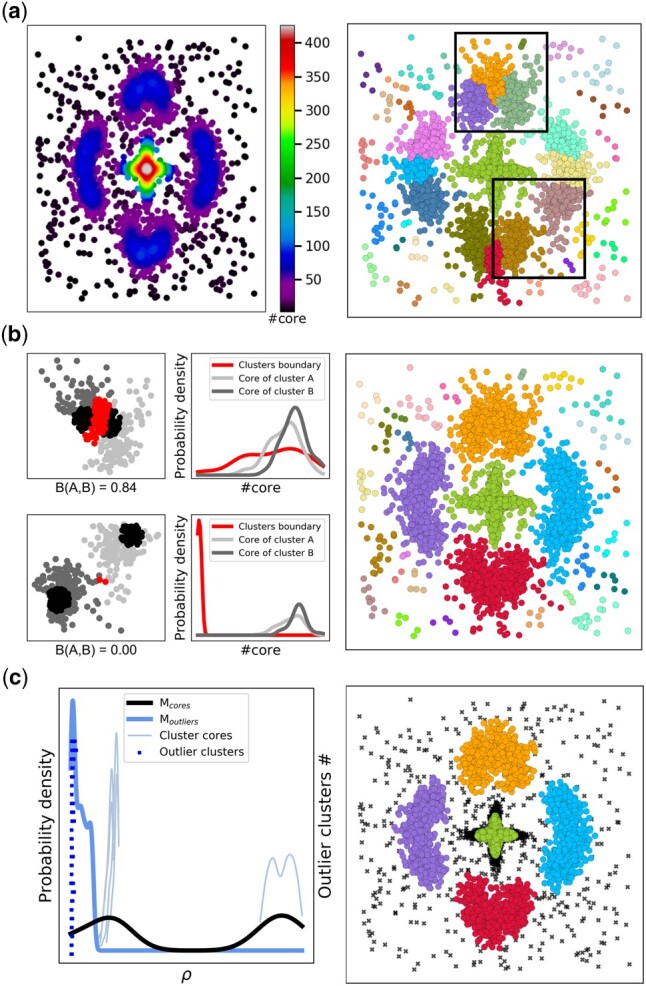
Clustering based on local density neighborhoods. We created a synthetic dataset that contains four croissant-shaped clusters of 500 elements each with different scaling as well as a cluster in the shape of a cross with 4000 elements and added Gaussian noise. (a) On the left, the cardinality of the core of each point in the dataset. On the right, the clusters obtained after the first stage of clustering. (b) The average Bhattacaryya coefficient B(A,B) between two Clusters A and B is shown. The upper left plots show an example of two clusters being merged corresponding to the upper square in panel (a). The lower left plots show an example of two clusters that will not be merged corresponding to the lower square in panel (a). Points belonging to the core of each cluster are shown in black, regular points in shades of gray and points belonging to the boundary in red. The plot on the right shows the clustering after merging clusters. (c) CLoNe uses a Bayesian classifier to decide if a cluster is genuine or arises from noise fluctuations. On the left, the corresponding probability density functions of points belonging to any cluster cores (black), noise (blue), or to individual cluster cores (light blue). The range of local density of clusters classified as noise fluctuations are shown on the secondary y-axis (dark blue). The final clustering result is shown on the right, with identified outliers shown as black crosses

One of the drawbacks of the DP algorithm is its limited ability to deal with clusters with more than one peak or those with an elongated region of similar density, such as the noisy circles benchmark dataset (Supplementary Fig. S2). This is true at this stage of CLoNe as well, as the Gaussian kernel in (1) is biased toward determining cores with spherical shapes (Fig. 1b). We can make the assumptions that if two existing clusters A and B should be merged, then the density from one core to the other should be relatively constant. This can be estimated by looking at the core cardinality distribution of the points belonging to the core of both clusters as well as that of the points from the boundary between them (Fig. 1b, left), which can be defined as:

$${\mathit{boundary}}_{AB}=\left\{i\in A,\mathrm{ }j\in B\right||d\left(i,j\right)<d_c\}$$ (3)

Then, we define the following probability density function for the ensemble of points belonging to either cluster cores or the boundary from (3): where S denotes one of the aforementioned ensembles and #core_i the core cardinality of point i and KDE refers to the probability density function estimated by unimodal Gaussian kernel density estimation. Similarity between probability distributions can be measured using the Bhattacharyya coefficient (BC) (Bhattacharyya, 1943), which is bound between 0 and 1. Thus, the formula to compute the BC between the core of cluster A with the boundary from (3) becomes:

• $P_s=\mathit{KDE}\left(\left\{{\#\mathit{core}}_i,i\in S\right\}\right)$     (4)

• ${BC}_A=\sqrt{P_{\mathit{bound}}{P}_{{\mathit{core}}_A}}$      (5)

We take the decision of merging Clusters A and B if the mean of their respective BC with their boundary is above a threshold ${\tau }_{BC}$:

$$B\left(A,\mathrm{ }B\right)=\mathrm{ }\frac{1}{2}\left({BC}_A+{BC}_B\right)>{\tau }_{BC}$$ (6)

where $P_{{\mathit{core}}_B}$ is obtained as for cluster A in (5) and ${\tau }_{BC}$ was chosen to be the 65th percentile to limit uncertainty and based on benchmarks (Fig. 1 and Supplementary Fig. S2). Taking the mean of both coefficients prevents the merging of a cluster whose probability density is similar to that of its boundary with a cluster of significantly higher density. This enabled us to identify clusters that can hardly be defined with a single density peak, such as uniform density over non-spherical shapes (Figs 1b and 2a). The point with highest ρ is chosen as the new cluster center. If p_dc is chosen too small, clusters may be split into sub-clusters. Within our approach, these sub-clusters are likely to be merged into clusters matching the original topology, expanding the range of acceptable values for p_dc and making it an input parameter less sensitive than the one of DPA (Supplementary Fig. S3).

The second drawback of using the Gaussian kernel in (1) is that it may falsely identify impromptu local noise fluctuations as cluster centers (Fig. 1b). To remedy this, we define two probability density functions. $M_{\mathit{cores}}$ is the probability density of the local density of all points belonging to any cluster core as per (2):

$$M_{\mathit{cores}}=\mathit{KDE}\left(\left\{{\rho }_x,x\in {\mathit{core}}_i\mathrm{ }\forall i\in C\right\}\right)$$ (7)

where C is the set of cluster centers remaining after the previous merging step. $M_{\mathit{outliers}}$ is the equivalent function for all points identified as outliers:

$$M_{\mathit{outliers}}=\mathit{KDE}\left(\left\{{\rho }_x,\mathrm{ }x\mathrm{ }\in X\mathrm{ }if\mathrm{ }{\rho }_x<f\times {\rho }_{{\mathit{center}}_x}\right\}\right)$$ (8)

where ${\rho }_{{\mathit{center}}_x}$ is the local density of the center of the cluster x belongs to and f an arbitrary fraction chosen to be 0.1 by default and used throughout this article. To determine if an identified cluster is more probable to be derived from noise than to be a genuine cluster, we use a Bayesian classifier. For each cluster core c_i, we derive the following posterior probabilities using Bayes’ theorem:

$$p\left(Y|c_i\right)=\frac{p\left(Y\right)\mathrm{ }p\left(c_i\right|Y)}{p\left(c_i\right)};Y\in \{\mathit{outliers},\mathrm{ }\mathit{cores}\}$$ (9)

where the prior probabilities are defined as follows:

$$p\left(Y\right)=\mathrm{ }\frac{\left|Y\right|}{N};\mathrm{ }Y\in \{\mathit{outliers},\mathrm{ }\mathit{cores}\}$$ (10)

where |Y| denotes the cardinality of the corresponding class. The likelihoods $p\left(c_i\right|Y)$ can be computed by evaluating the previously defined probability distributions (7) and (8) at $c_i$. Disregarding the evidence $p\left(c_i\right)$ common for both outliers and cores classes, we thus obtain the following Bayesian classifier:

$$\widehat{y_i}=\underset{Y\in \left\{\mathit{outliers},\mathrm{ }\mathit{cores}\right\}}{\mathrm{argmax}}p\left(Y\right){\prod }_{x\in c_i}{M}_Y\left({\rho }_x\right)$$ (11)

This classifier enabled us to remove all cluster centers arising from noise fluctuations. Combined with the previous merging step, the clustering is now complete (Fig. 1c).

The software has been written using Python3.7. When used on structural biological data, CLoNe outputs cluster centers as separate PDB files, individual clusters as XTC trajectories and Tcl scripts for automated loading within the visualization software VMD (Visual Molecular Dynamics, (Humphrey et al., 1996)). The loading of MD trajectories as well as the saving of cluster centers and cluster sub-trajectories is done through the MDTraj package (McGibbon et al., 2015). We use the scipy (Jones et al., 2001), scikit-learn (Pedregosa et al., 2011) and Statsmodels (Seabold and Perktold, 2010) packages for many operations described in the previous subsection and to compare CLoNe to other clustering algorithms.

3 Results

3.1 Automatic cluster center determination from local density neighborhood analysis

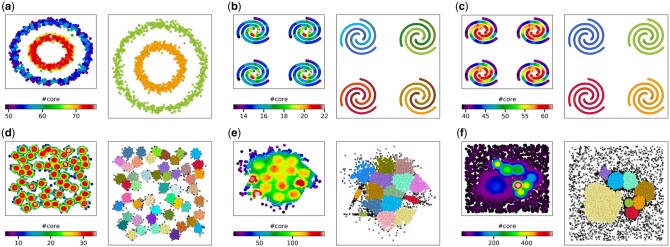
We applied CLoNe to a large set of common benchmark datasets from various sources (Chang and Yeung, 2008; d’Errico et al., 2018; Fränti and Sieranoja, 2018; Fu and Medico, 2007; Gionis et al., 2007; Pedregosa et al., 2011), covering different key properties of clusters, such as non-spherical shapes, anisotropy, as well as significant size and density differences, all of which can be expected from real-world datasets from structural biology. In the previous section, we detailed how CLoNe automatically detects cluster centers, accurately merges clusters and removes outliers, succeeding in cases where previous iterations of DP did not (Fig. 2a and Supplementary Fig. S2). Similarly to the original DP algorithm (Rodriguez and Laio, 2014), CLoNe requires a single input parameter p_dc, which relates to a cutoff distance used in the estimation of local densities (see Section 2). In general, p_dc takes a value in a small range and is intuitive to set. For instance, with p_dc values of 1 or 2 local densities will be estimated considering neighborhoods small enough to identify individual spiral branches as clusters (Fig. 2b). For higher values of p_dc, the scale of the Gaussian kernel in Equation (1) will increase and merge individual branches into whole spirals, allowing the study of multiple hierarchies intuitively (Fig. 2c). Other than clusters with non-spherical shapes, CLoNe identifies successfully the numerous Gaussian clusters of the A3 dataset (Fig. 2d). Some degree of overlapping in real-world datasets is to be expected. The S4 dataset contains 15 highly overlapping Gaussian clusters of varying densities and shapes but equal size. As with the A3 dataset, CLoNe does not perform unnecessary merging with nearby clusters (Fig. 2e) and is robust to large amounts of outliers on top of clusters with significantly different densities (Fig. 2f). This general applicability of CLoNe coupled with a single, robust and easy to set input parameter (Supplementary Fig. S3) is unique among the commonly used clustering algorithms found in the Scikit-learn package (Pedregosa et al., 2011). In fact, CLoNe is among the fastest algorithms from that package in addition to both DP and DPA and the most accurate on the available benchmark cases (Supplementary Fig. S2). The only other algorithm succeeding on all benchmark cases is OPTICS (Ankerst et al., 1999), which runs slightly slower than CLoNe on these datasets and tends to classify too many points as outliers. Similar to the original implementation of DP, CLoNe is applicable to high dimensionality datasets as well (Supplementary Table S1 and Supplementary Fig. S4).

Fig. 2.

Local neighborhood density analysis for automated center and cluster determination. For each panel, the cardinality of the core of each point as detailed in the Section 2 is shown on the left. The resulting clusters are shown on the right, with clusters in different colors and identified outliers as black crosses. (a) Noisy circles dataset. (b and c) Four instances of spiral dataset with different values of the input parameter yielding different yet valid clusters. (d) The a3 dataset containing 50 Gaussian clusters. (e) The s4 dataset with highly overlapping Gaussian clusters, some with anisotropic distributions. (f) A synthetic dataset with clusters of significantly different sizes and densities taken from Density Peaks Advanced

One of the principal aims of this work is to offer a clustering algorithm able to classify unlabeled biological structural ensembles into relevant states associated with their function and mechanism of action. We have applied CLoNe to real-world structural biology data reporting on the dynamic conformational space of a protein that associates with its specific biological membrane, cryptic allosteric pocket opening and dimerization of transmembrane proteins.

3.2 Determining relevant states within protein conformational ensembles

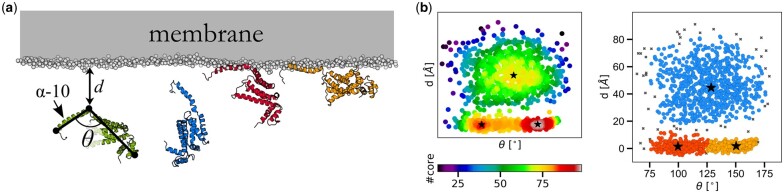
COQ9 is a lipid-binding protein associated with the biosynthesis of coenzyme Q (CoQ), a redox-active lipid that is essential for cellular respiration (Lohman et al., 2014). Recently, coarse-grained molecular dynamics (CG-MD) simulations and liposome co-flotation assays were used together to reveal that COQ9 accesses membranes in a multi-step fashion through a distinct, C-terminal amphipathic helix (α10) (Lohman et al., 2019). In these simulations, COQ9 first diffused in the aqueous environment, then underwent various conformational changes upon membrane binding (Lohman et al., 2019). We applied CLoNe to the CG-MD trajectory used in the latter study and sought to identify the main binding events pertaining to the protein itself. To this end, we extracted features characterizing both its movements in the aqueous environment through monitoring its distance to the membrane as well as key conformational changes based on the angle between the unique α10 helix of COQ9 and its globular domain (Fig. 3a, left). Using these two features, CLoNe outputs three clusters, each of which seem to follow Gaussian distributions (Fig. 3b). One cluster regroups all conformations that correspond to diffusion movements in the aqueous environment, while the other two highlight the membrane association of α10 first followed by the globular domain as a converging step (Fig. 3a), thus its higher density (Fig. 3b). Similar results can be obtained hypothesis-free by using raw atomic spatial coordinates (Supplementary Fig. S4). The Gaussian distribution of structural clusters has also been observed in a recent study from our group involving the KAP1 protein, where CLoNe was also successfully applied (Supplementary Fig. S5) (Fonti et al., 2019).

Fig. 3.

Utilizing Gaussian cluster properties to extract centers as key biological states of the COQ9 membrane protein. (a) COQ9 and its associated features, which include an internal angle θ and its distance to the membrane d (left). Cluster centers are shown on the right side of the panel. (b) Every frame is plotted in the mentioned feature space and color coded according to their core cardinality (left) and cluster assignation (right), which follows the same color code as in (a). Outliers are shown as black crosses and centers as black stars

3.2 Isolating sub-ensembles of relevant conformations for ligand–target interactions

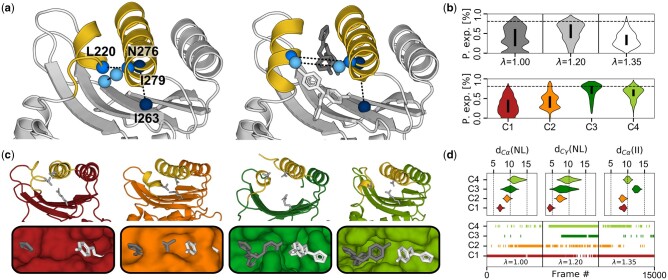
In recent years, small-molecule docking software is no stranger to dynamics, taking into account ensembles of ligand conformations (Amaro et al., 2018) or receptor flexibility (Kokh et al., 2011; Salmaso and Moro, 2018; Vahl Quevedo et al., 2014). A recent study highlighted a novel replica exchange-based MD protocol combined with benzene probes, where each replica harbors a different scaling of water–protein interactions (Oleinikovas et al., 2016). Using this method, the authors could observe the opening of cryptic allosteric pockets in several systems, including that of the TEM1 β-lactamase, which plays a critical role in antibiotic resistance (Horn and Shoichet, 2004). The simulations were started from the apo crystal structure with a closed allosteric pocket (Fig. 4a). Out of the eight replicas of the simulation, we chose three with neutral (first), medium (fourth) and highest (last) scaling factors as a tradeoff between maximizing the sampled conformational space and limiting redundancy of the over-represented closed conformations (Oleinikovas et al., 2016) (Fig. 4b). Along with key residue R244 on the opposite wall of the pocket, the opening of α-helices H11 and H12 and key residues L220 and N276 dictate pocket opening and allow two inhibitors to be accommodated (Horn and Shoichet, 2004), while the three mentioned residues form a triad when the pocket is closed. In addition to the opening of the two helices, visual inspection of the simulations indicated a deepening of the pocket. As a result, we chose features tracking the distance between the Cα of residues L220 and N276 as well as that of their sidechains to monitor pocket opening as well as the distance between the Cα of I263 and I279 as a measure of pocket depth (Fig. 4a). The original study used fpocket (Le Guilloux et al., 2009) to monitor pocket exposure in each replica (Fig. 4b, top). The same was done on the clusters obtained by CLoNe (Fig. 4b, bottom), showing different levels of pocket openness. Corresponding cluster centers highlight key structural differences between each state (Fig. 4c), which are representative of the feature distribution per cluster (Fig. 4d, top). Cluster assignation follows the observation of the original publication, where open states were more prevalent in the replica of medium scaling (Fig. 4d, bottom).

Fig. 4.

Identification of different opening states of the allosteric cryptic pocket in TEM1 β-lactamase. (a) apo and Holo structures (left and right, respectively). Allosteric inhibitors are shown in gray and white. Features following helical opening include the distance between Cα atoms of N276 and L220 (medium blue) and the Cγ of their sidechain (light blue). Pocket depth is monitored by the distance between Cα-carbons of I263 and 279 (dark blue). (b) The pocket exposure calculated using the fpocket software for the original replicas (top) and for each clusters (bottom). The dotted line in both is the reference value of the holo crystal structure used in the original paper. (c) The center of each cluster in cartoon representation on top of a surface representation of the allosteric pocket, highlighting the different states of helical openness and pocket depth. The triad N276-L220-R244 governing pocket opening and closing are shown as gray sticks. (c) The distribution of each feature for each cluster (top) and the cluster assignation along the three chosen replicas (bottom)

3.3 Identifying dominant conformational motifs in protein oligomerization

Another challenge in structural biology is the understanding of how biomolecules oligomerize to distinctive functional states. One of these cases, the transmembrane α-helix of the Amyloid Precursor Protein (termed APP hereafter), has recently been studied by our lab through the high-throughput MD protocol DAFT (Docking Assay For Transmembrane components, (Wassenaar et al., 2015)) in order to identify which of two dimerization motifs is promoted depending on the lipid composition of the synaptic plasma membrane (Audagnotto et al., 2016). The G₇₀₀G₇₀₄G₇₀₈ motif is thought to direct the binding of APP to regulators promoting cholesterol biosynthesis, while the G₇₀₉A₇₁₃ motif would bind to cholesterol molecules (Fig. 5a). Extracting features from molecular datasets is not always straightforward. Macromolecular movements possess an inherent redundancy due to the sheer number of internal degrees of freedom or prior knowledge may be lacking in order to select meaningful features, such as those highlighted in Figures 3 and 4. The use of dimensionality reduction methods, such as principal component analysis (PCA) has been seen for clustering of MD simulations (Wolf and Kirschner, 2013) and can help identifying coordinates of significance while discarding less useful dimensions. The DAFT simulations of APP from (Audagnotto et al., 2016) are over 2 ms in total and contain countless states, many corresponding to unbound monomers. The first principal component based on the Cartesian coordinates of the coarse grain backbone covers 77% of the variability in the simulation, highlighting two clusters (Fig. 5b). The blue cluster of lower amplitude corresponds to all states exhibiting unbound monomers (Fig. 5e, left), while the second cluster regroups all the dimerized states regardless of motif. Focusing on that cluster, we calculated the pair-wise distances between the backbone atoms of each motifs in both helices (Fig. 5a) and reduced these features to a two-dimensional principal space covering 94% of the variability before clustering (Fig. 5c). We want to highlight CLoNe’s ability to analyze the neighborhood of low-density clusters without influence from high-density regions (Fig. 5c and Supplementary Table S2). Clusters in blue in Figure 5d all depict states close to the G₇₀₀G₇₀₄G₇₀₈ motifs and those in green the G₇₀₉A₇₁₃ motif. In the middle are two clusters, shown in brown, that we interpret as hybrid. In all cases, the darker-shaded clusters of each group correspond to the closest to the optimal motif arrangement, while the others can be considered as closely related metastable states (Supplementary Fig. S6). Similar to the original study (Audagnotto et al., 2016), CLoNe finds the preferred dimerization motif to be G₇₀₀G₇₀₄G₇₀₈ as evidenced by the corresponding centers’ local densities, cluster population and core cardinality (Fig. 5c and Supplementary Table S2). A comparison between CLoNe and other state-of-the-art algorithms on all the structural data shown in this section demonstrates the advantages of CLoNe for analysis of molecular structural ensembles (Supplementary Fig. S7).

Fig. 5.

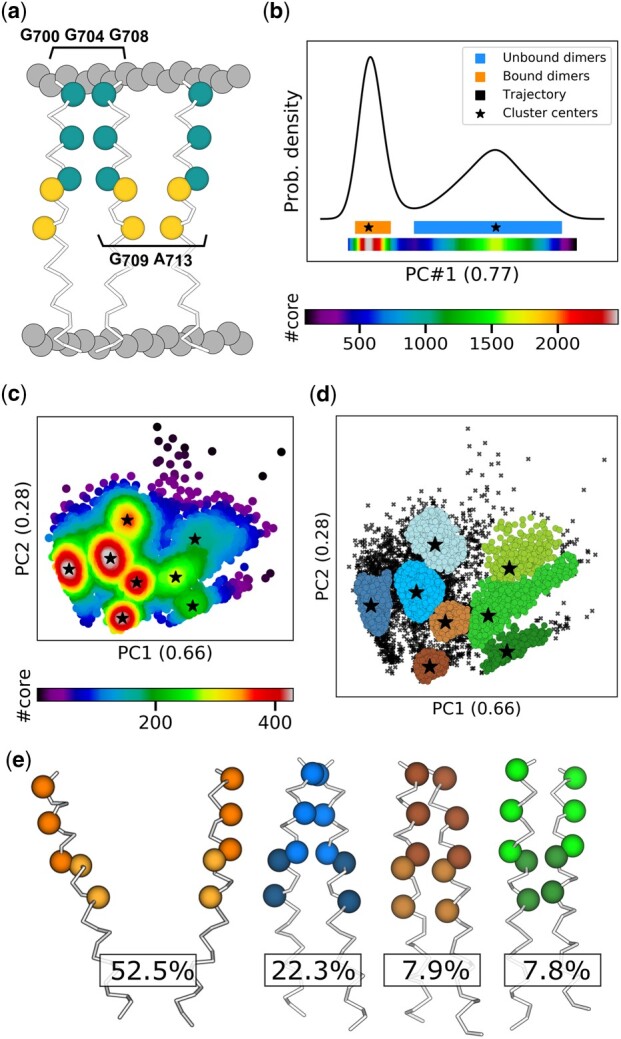
Classification and frequency estimation of APP dimerization motifs in the plasma membrane. (a) The two known dimerization motifs of the transmembrane helix of APP. Membrane is depicted with gray spheres, the G₇₀₀G₇₀₄G₇₀₈ motif with teal spheres and the G₇₀₉A₇₁₃ motif with gold spheres. (b) The black line depicts the probability density distribution of the trajectory along the first principal component, which covers 77% of variability. Obtained clusters are shown in colors underneath, with their centers as black stars. Below the clusters is the distribution of core cardinalities, with the corresponding color bar below it. (c) The cluster of bound dimers of (b) was extracted and the pair-wise distances between the backbone atoms of each motifs in both helices was computed for every frame. The plot shows the first two principal components of the resulting dataset (with eigenvalues of 0.66 and 0.28, respectively), where each point is color-coded according to the cardinality of its core. Stars represent cluster centers. (d) The clusters obtained from the aforementioned dataset of bound conformations. (e) Renders of the unbound and dimerized APP cluster centers and their respective frequency after outlier removal. Dimerized APP centers shown correspond to the dark blue, dark brown and dark green clusters. Sidechains have been hidden for better visualization

4 Discussion

Many clustering methods rely on parameters that are often non-trivial to optimize or on random initial conditions that may drastically change the outcome. Commonly used algorithms are generally restricted to specific cluster properties, forcing the researcher through a process of trial and error. Moreover, choosing relevant features from structural datasets is challenging and different features may generate different cluster topologies, sometimes irrelevant. CLoNe was designed with these issues in mind and aims to provide a stream-lined analytic process to yield results rapidly along with helpful visualization scripts to analyze and confirm the relevance of the clusters in the target biological context (Supplementary Fig. S1). CLoNe’s only parameter regulates the size of the local neighborhood considered around each data point, which can be regarded as cluster sizing parameter. Its value need only be decreased if clusters seem too inclusive and vice-versa, making CLoNe an intuitive algorithm to use in addition to its general applicability. For structural datasets, CLoNe is able to extract clusters as separate trajectories and provides scripts for their automatic loading in the visualization software VMD (Humphrey et al., 1996). For larger macromolecules, the concept of a conformational state is blurry, hard to determine and often depends on context. It is not always clear which features to use to obtain an accurate partition of the structural ensemble. The results obtained on COQ9 can be obtained hypothesis-free on raw spatial coordinates or using PCA to extract relevant features (Supplementary Fig. S4). This was done in the case of APP as well as to reduce an otherwise redundant feature space to one of lower dimensionality. If one wishes to disentangle internal from overall motion, dihedral PCA was used with success to study peptide folding (Altis et al., 2007; Mu et al., 2004). However, when other features than the chosen ones can be expected to exhibit motions of larger amplitudes, PCA will favor the latter over the former. This is true for the TEM1 β-lactamase, where internal structural motions will be more prevalent than the fluctuations of the selected key pocket residues. In such cases, a feature-based approach is to be preferred. Alternatively, some will advocate the use of time-lagged independent component analysis (TICA) (Naritomi and Fuchigami, 2011) instead. TICA was found to be the better alternative for building Markov state models (Husic and Pande, 2018; Pérez-Hernández et al., 2013). However, in cases where large amplitude fluctuations are the target or when there is redundancy in features, we believe that PCA remains a safe approach.

As the conformational ensembles presented in this study tend to exhibit Gaussian distributions, CLoNe may thus be used to extract cluster centers as higher probability states. Such states offer an overview of the ensemble and may serve as starting models for building Markov state models in general. Moreover, the precision of the classification achieved by CLoNe enables the identification of dominant biological states from large datasets. Beyond the case of APP, CLoNe identified different key pocket conformations in the case of TEM1 β-lactamase. Further clustering efforts on this system should target the different positions of R244, which was not tracked in this study but was previously shown to play a dual role between TEM1’s active site and allosteric pocket (Horn and Shoichet, 2004). CLoNe may then be used as a pre-processing tool prior to small-molecule docking studies, where accounting for receptor flexibility is an active development area (Kokh et al., 2011; Vahl Quevedo et al., 2014).

Integrative modeling aims at incorporating data from multiple sources to determine the structure of macromolecular complexes. Such hybrid strategies typically combine low resolution data of whole complexes with high resolution structures of their components so as to predict the quaternary structure of the former (Cassidy et al., 2018). This process is however severely hindered by structural dynamics differing between a complex and its isolated components. For this reason, many hybrid modeling strategies now incorporate some form of dynamics to bridge this gap (Malhotra et al., 2019; Tamò et al., 2015). While we previously utilized classical MD for the prediction of heptameric aerolysin pores (Degiacomi et al., 2013; Degiacomi and Dal Peraro, 2013), such an approach would not be feasible for heteromultimeric assemblies where multiple conformational ensembles are required simultaneously. Reducing them to their crucial components may enable the structural characterization of large macromolecular complexes, which may otherwise be intractable. Applied to the fields of small-molecule docking, integrative modeling and structural dynamics studies, CLoNe presents itself as a versatile and powerful tool for modern computational structural biology.