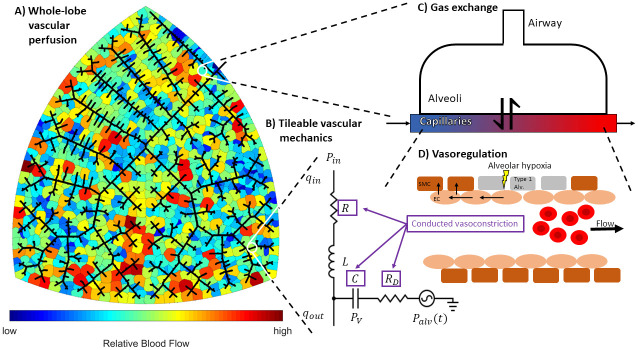
Fig 1. Schematic of our multi-scale multi-physics model of ventilation-perfusion matching.

Block (A) illustrates the whole-lobe vascular network model. Black lines represent blood vessels, and colored regions represent discrete zones of perfusion. The network geometry is agnostically generated by a space-filling algorithm inspired by Wang et al. [33]. Block (B) shows how the mechanics of each vessel segment is represented as an equivalent circuit. Intravascular pressure (P_v) and flow into the vessel (q_in) are the state variables; inlet pressure (P_in) and flow out of the vessel (q_out) are the initial conditions at boundaries for a given vessel segment; outlet pressure (P_out) is an algebraic constraint; time-varying alveolar pressure (P_alv) is a dynamic pressure source; and hydraulic resistance (R), inertance (L), compliance (C), and vessel wall resistance (R_D) are anatomical parameters calculated from the geometry of the vessel segment (length and radius) and can be modulated by vasoregulation (purple boxes). Block (C) depicts a representative gas exchange unit. Gases flowing through the capillary tube are exchanged with an alveolar compartment. Block (D) portrays the oxygen-sensitive vasoregulatory mechanism hypoxic pulmonary vasoconstriction (HPV). Hypoxia in the alveolar space induces conducted vasoconstriction. Conducted vascular responses are spatially propagated in a upstream through the endothelium—these responses modulate the values of the anatomical parameters (R, C, and R_D) in the arterial network.