Abstract
Deep learning (DL) approaches are part of the machine learning (ML) subfield concerned with the development of computational models to train artificial intelligence systems. DL models are characterized by automatically extracting high-level features from the input data to learn the relationship between matching datasets. Thus, its implementation offers an advantage over common ML methods that often require the practitioner to have some domain knowledge of the input data to select the best latent representation. As a result of this advantage, DL has been successfully applied within the medical imaging field to address problems, such as disease classification and tumor segmentation for which it is difficult or impossible to determine which image features are relevant. Therefore, taking into consideration the positive impact of DL on the medical imaging field, this article reviews the key concepts associated with its evolution and implementation. The sections of this review summarize the milestones related to the development of the DL field, followed by a description of the elements of deep neural network and an overview of its application within the medical imaging field. Subsequently, the key steps necessary to implement a supervised DL application are defined, and associated limitations are discussed.
Index Terms—: Classification, convolutional neural networks (CNNs), deep learning (DL), medical imaging, segmentation, synthesis
I. Introduction
DEEP learning (DL) evolved from the machine learning (ML) subfield, which is part of the computer science branch known as artificial intelligence (AI). The goal of any AI system is to learn from its environment without being programmed to identify any specific patterns of it. Thus, AI systems can be seen as rational agents that “act so as to achieve the best outcome or, when there is uncertainty, the best-expected outcome” [1]. ML is the AI subfield concerned with the development of approaches to train AI systems [2]. Specifically, ML models learn by exposing the algorithm to an input dataset that has a matching output dataset—the objective of the ML model is to learn the relationship between the input and output datasets. Some established ML approaches include decision tree learning [3], reinforcement learning [4], and Bayesian networks [5]. An essential characteristic of ML models is that it requires a feature engineering step to reduce the dimensionality of the input data to select the best latent representation of the data for the training process. This can be a time-consuming operation with potentially indeterminate outcomes, requiring the practitioner to have some domain knowledge of the data. As a result, DL approaches were designed to overcome this challenge by automatically extracting high-level features from the input data [6]. This advantage of DL over ML dramatically simplifies the training process by eliminating the feature extraction step.
An area that has greatly benefited from this advantage is the medical imaging field in which most of the available data poses an uncertain nature, thus making it difficult, sometimes impossible, to know which features are relevant to the problem at hand. Currently, most of the DL applications within the medical imaging field are narrow, thus trained to solve very specific problems. Some of the most common applications include image classification, regression, segmentation, and synthesis. Applications of DL can be generally divided into two learning approaches: 1) supervised and 2) unsupervised [7]. In the supervised learning approach, there is a matched pair of data to train the model. For example, inputting positron emission tomography (PET) brain images of patients with and without Alzheimer’s disease into a DL model as two distinct classes for classification. Conversely, an unsupervised learning process is characterized for not possessing the same constraint (no matching data is included) [8], allowing the model to determine which are the important features within the dataset and how many distinct classes are present. While the former approach may be advantageous for some applications, in the case of medical imaging data, releasing the constraint offered by matching data may cause the DL model to find patterns that may not necessarily correlate with the clinical interpretation of the data. As a result, most applications of DL models for medical imaging have utilized supervised learning or a hybrid combination of both—unsupervised learning techniques have also been combined with common ML methods. For that reason, in this review, we attempt to present an overview DL and provide a guide on how to successfully implement DL techniques for medical imaging. To that end, Section II summarizes the elements of deep neural networks. Section III includes an overview of DL application in medical imaging. Furthermore, the steps needed to train a neural network are included in Section IV, followed by a discussion of robustness (Section V) and limitations (Section VI).
II. Elements of Deep Neural Networks
A. What Is Deep Neural Network?
Deep neural networks and DL have become a highly successful and popular research topic because of their excellent performance in many benchmark problems and applications [9], especially in the fields of the control system, natural language processing, information retrieval, computer vision, and image analysis [6], [10], [11]. Kohonen [12] gave a widely used definition in 1988 as follows:
“Artificial neural networks are massively parallel interconnected networks of simple (usually adaptive) elements and their hierarchical organizations which are intended to interact with the objects of the real world in the same way as biological nervous system do.”
1). Historical Development of Deep Neural Networks:
Neural networks have been studied for many years. In 1943, McCulloch and Pitts [13] put forward the famous M-P neuron model, which described artificial neurons with Boolean inputs and a binary output. In 1949, Hebb [14] introduced a learning rule that described how the connection between neurons was affected by neural activities, which could be used for updating weights of neural networks. In 1958, Rosenblatt [15] applied the Hebb rule to the M-P model and proposed the perceptron idea, which performed well in solving logic conjunction, disjunction, and negation problems. However, in 1969, Minsky [16] pointed out that the single-layer perceptron could not solve the logic exclusive disjunction problem. However, the multilayer perceptron (MLP) could, but there were no learning rules for updating weights of MLP, which made the research on neural networks sluggish for many years. Inspired by Hubel and Wiesel’s work [17]–[19], Fukushima [20] invented the neocognitron network in 1980 based on the previous work, the cognitron [21]. The neocognitron is a hierarchical and multilayer neural network, which holds many similarities to modern convolutional neural networks (CNNs). In 1985, Rumelhart et al. [22] supplied the backpropagation algorithm, which solved the MLP’s training problems. In 1989, LeCun et al. [23] applied the backpropagation algorithm to the training of multilayer neural networks named LeNet applied to identify handwritten numerals. In 1998, LeCun [24] put forward the LeNet-5, which presaged the coming of CNNs. In 2006, Hinton et al. [25] proposed the deep belief network (DBN), which gave a solution to the training of deep neural networks. In 2012, Krizhevsky et al. [26] created AlexNet and won the ImageNet competition (to perform visual object recognition from photographs). AlexNet was a historical breakthrough in neural network performance and capability. Since then, neural networks have undergone rapid development and developed in four main directions: 1) increasing the depth (number of layers) of neural networks, like the VGGNet [27]; 2) reinforcing the convolutional layer’s function, like the GoogleNet [28]; 3) transferring tasks from classification to detection, like the RCNN [29], Fast RCNN [30], and Faster R-CNN [31]; and 4) adding new functional modules, like FCN [32], UNet [33], and STNet [34].
2). Multilayer Perceptron:
The MLP is also called a feed-forward neural network (FNN) and defines the basic model of deep neural networks. It defines a map between the input x and the ground truth y, aiming at learning the parameters θ and getting the approximation of the function f. As shown in Fig. 1(b), the MLP is composed of multiple layers, including the input layer, hidden layer, and output layer. Each layer contains multiple neurons, the building block of deep neural networks. Neurons in adjacent layers are connected with each other while those in the same layer are independent.
Fig. 1.
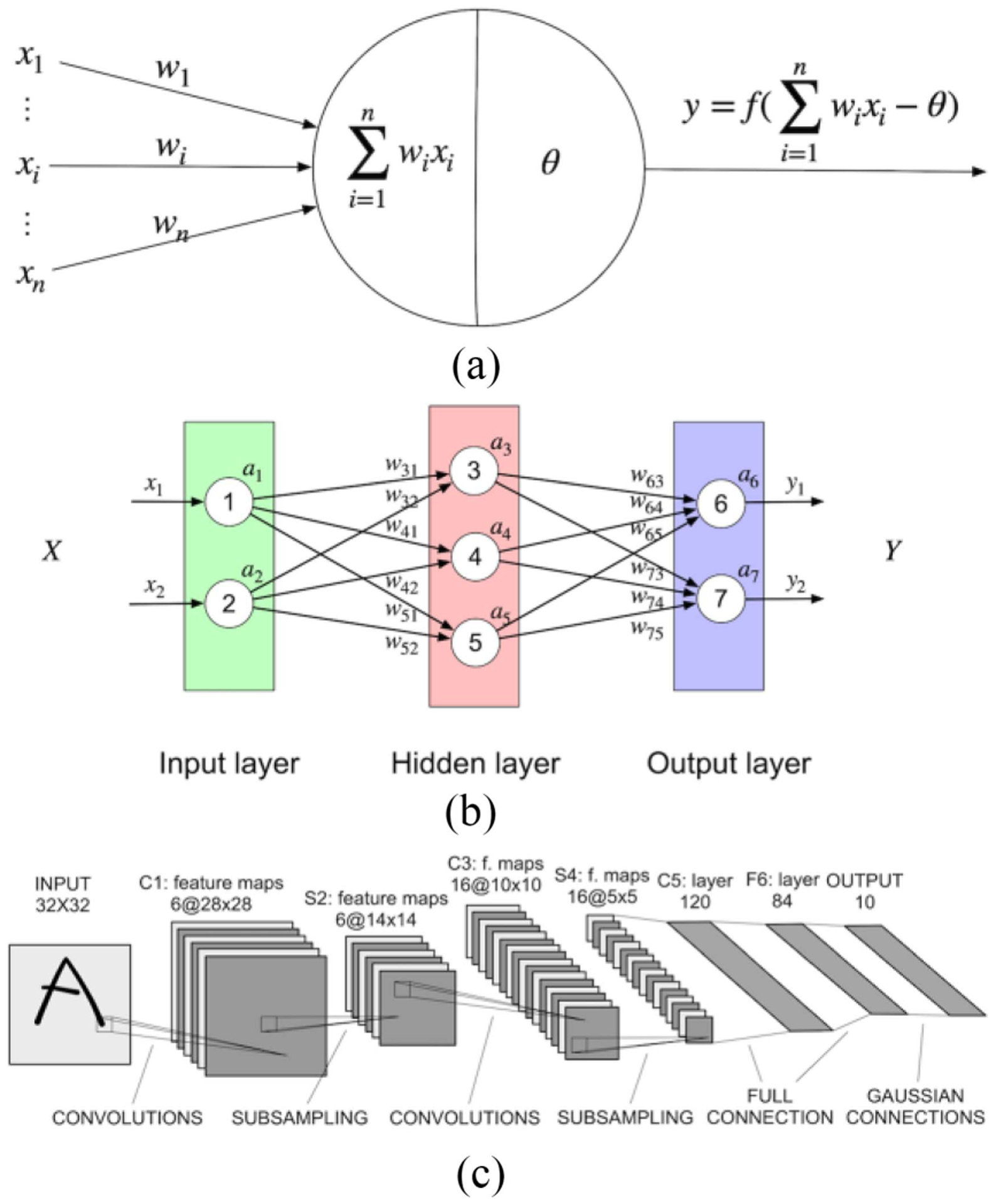
(a) Structure of the McCulloch and Pitts neuron model. xi stands for the input of the neuron, wi stands for the corresponding weight. θ means the bias which is related to decide whether this neuron should be activated or not. (b) Structure of the MLP. (c) Structure of the LeNet5 model, designed for character recognition.
The training of the MLP includes two stages, the forward propagation and the backpropagation.
Stage 1 (Forward Propagation):
For a single neuron, the M-P neural model is shown in Fig. 1(a). xi means the ith input of the neuron and wi means the corresponding weight of the ith input. θ is the threshold. f is the activation function, which decides whether the neuron is in an active or inactive state. From the M-P neural model, if f is defined as , then it means the neuron will be activated if the weighted sum of inputs is larger than the threshold (θ). Otherwise, it will remain silent.
Therefore, the forward propagation of MLP can be presented as follows:
| (1) |
| (2) |
is the output of the ith neuron in the lth layer. is the jth neuron’s value in the (l + 1)th layer before being activated. is the weight between the ith neuron in the lth layer and the jth neuron in the (l + 1)th layer. is the bias. f is the nonlinear activation function, like the Sigmoid, Tanh, and ReLU.
Stage 2 (Backpropagation):
The backpropagation algorithm is designed for updating the weights of the MLP based on the loss obtained by comparing the difference between the MLP’s output and the ground truth. Lower loss and a better model can be achieved by properly tuning hyperparameters, which is typically determined manually prior to training. A growing area of the field is a focus on the automation of hyperparameter optimization [35].
Loss functions and optimization methods are highly flexible and important during the training process. How to choose a suitable loss function and optimization method is described in Section IV-C “network training and validation.” If the squared error is used for measuring the difference between the MLP’s output and the ground truth, the loss can be obtained through the following formula. L is the number of layers in MLP. means the jth neuron’s output in the final layer, Lth layer
| (3) |
If the gradient descent optimization function is chosen as the optimization method, then the weights can be updated in such a way as shown in the following formula. η is the learning rate
| (4) |
According to the chain rule, the update rule for the output layer can be computed as follows:
| (5) |
Then, the updated weights of the last layer can be computed in the following way:
| (6) |
However, for the hidden layer, the update rule is slightly different
| (7) |
If we define
| (8) |
Then
| (9) |
Thus, the relationship between and can be represented as such
| (10) |
Finally, the update formula for the weights of the hidden layers is shown as follows:
| (11) |
In summary, the training loss will be computed after the forward propagation. Based on the loss, the parameters of each layer will be updated in the backpropagation according to certain rules.
B. Type of Deep Neural Network Layers
Fig. 1(c) shows the architecture of the LeNet-5 CNN, which was initially proposed for handwritten character recognition [24]. CNNs are composed of a sequence of layers, including multiple layers, such as a convolutional layer, a pooling layer, a fully connected layer, and an activation layer. Data size is usually reduced or downsampled pooling layers. Therefore, if data size needs to be upsampled, transpose convolution layers or upsampling layers are needed. In addition to these basic types of layers, there are some other advanced layers, such as the normalization layer and the dropout layer, which are designed for specific purposes, such as facilitating training and avoiding overfitting. Additionally, operations can happen not only between adjacent layers but also between nonadjacent layers, through operations, such as concatenation. Therefore, deep neural networks can be arbitrarily complicated. However, no matter how complex the network architecture might be, the individual layers are typically made up of common elements. We now describe common layers used in contemporary deep neural networks.
1). Convolutional Layer:
The convolutional layer is the key foundation of the CNN. The input of this layer can be the input images or feature maps. The parameters in this layer consist of learnable filters, also called kernels which are to be learned during training. Each filter usually has the same depth as the input images or feature maps have, but much smaller height and weight. The height and width (and depth, if applicable) of each kernel should be set manually in advance— 3 × 3 is the most commonly used shape. However, note that cascaded small kernels have the same receptive field (i.e., the area in the input involving convolution calculation and producing features) but with less parameters. For example, two cascaded 3×3 kernels only have 18N (N is the factor unrelated to the kernel size) parameters needed to be trained, but the receptive field is the same as one 5×5 kernel, which contains 25N parameters. A 1×1 filter is also possible and is equivalent to applying an affine transformation to the feature maps, which allows the exchange of information at different depths and increasing nonlinearity. As Fig. 2(a) shows, in the forward pass, each filter will move from the left to right first, then up to down. The distance between each move is called stride. Before each move, the dot products between the filter and the corresponding area will be computed and compose one feature map. The visualization of the feature map of various convolutional layers is shown in Fig. 3, as obtained from Meng et al. [36]. It can be concluded that the shallow convolutional layers generally detect the edge and color features while deeper ones generally combine the features from the shallow ones to get more specific features, like the wheel of the car. However, in this way, the image will become smaller and smaller and the boundary information will be lost. To solve this problem, zero padding is introduced by adding zeros to the left and right, up and down symmetrically. Then, the output shape of the convolutional layer can be computed by the following formula. The default value for dilation is typically 1
| (12) |
Fig. 2.
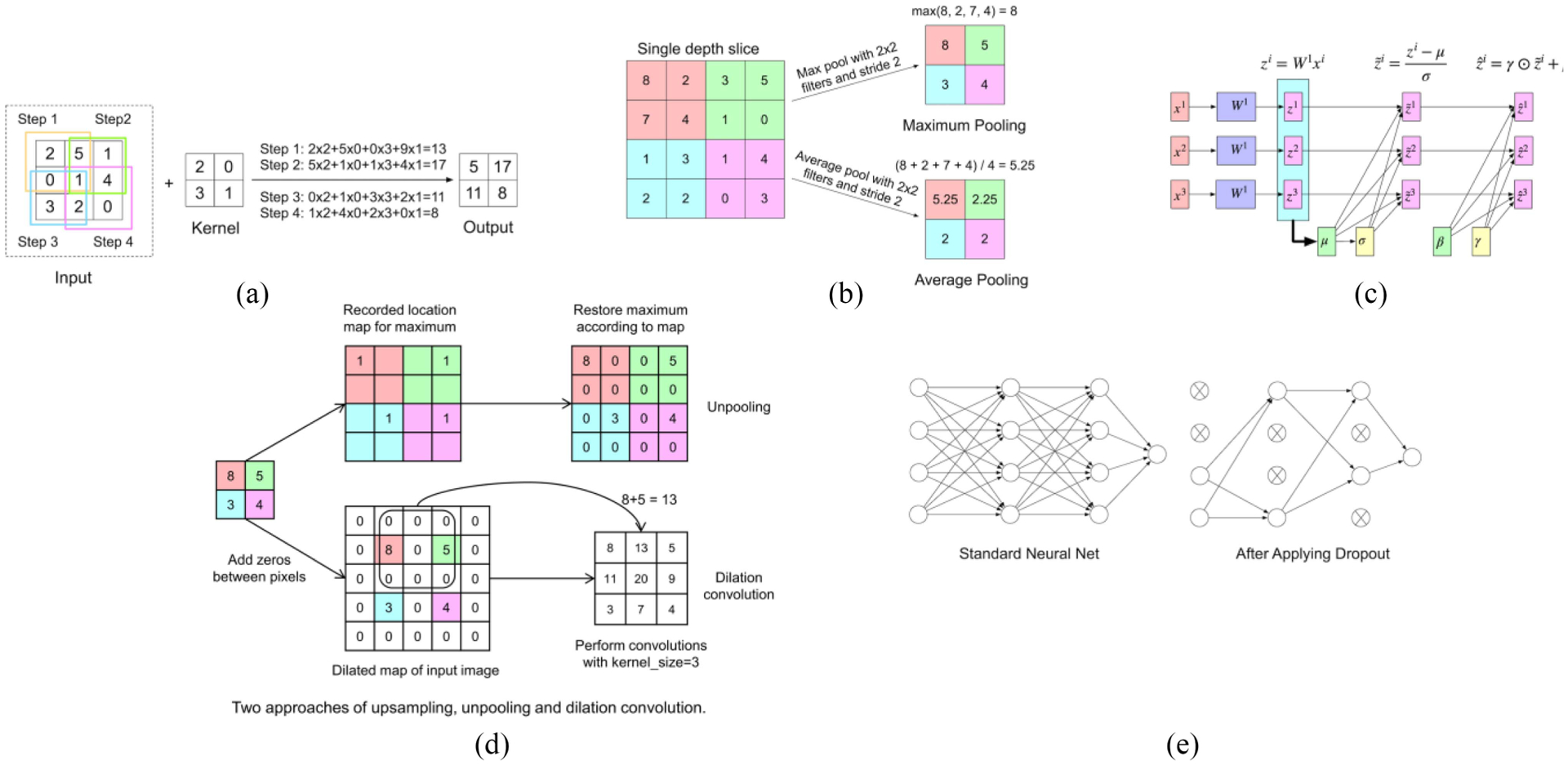
Graphical depiction of several layers from a CNN. (a) Convolutional layer. (b) Max-pooling and averaging pooling layers for downsampling. (c) Pipeline of a batch normalization layer. (d) Unpooling and dilation convolution layers for upsampling. (e) Dropout.
Fig. 3.
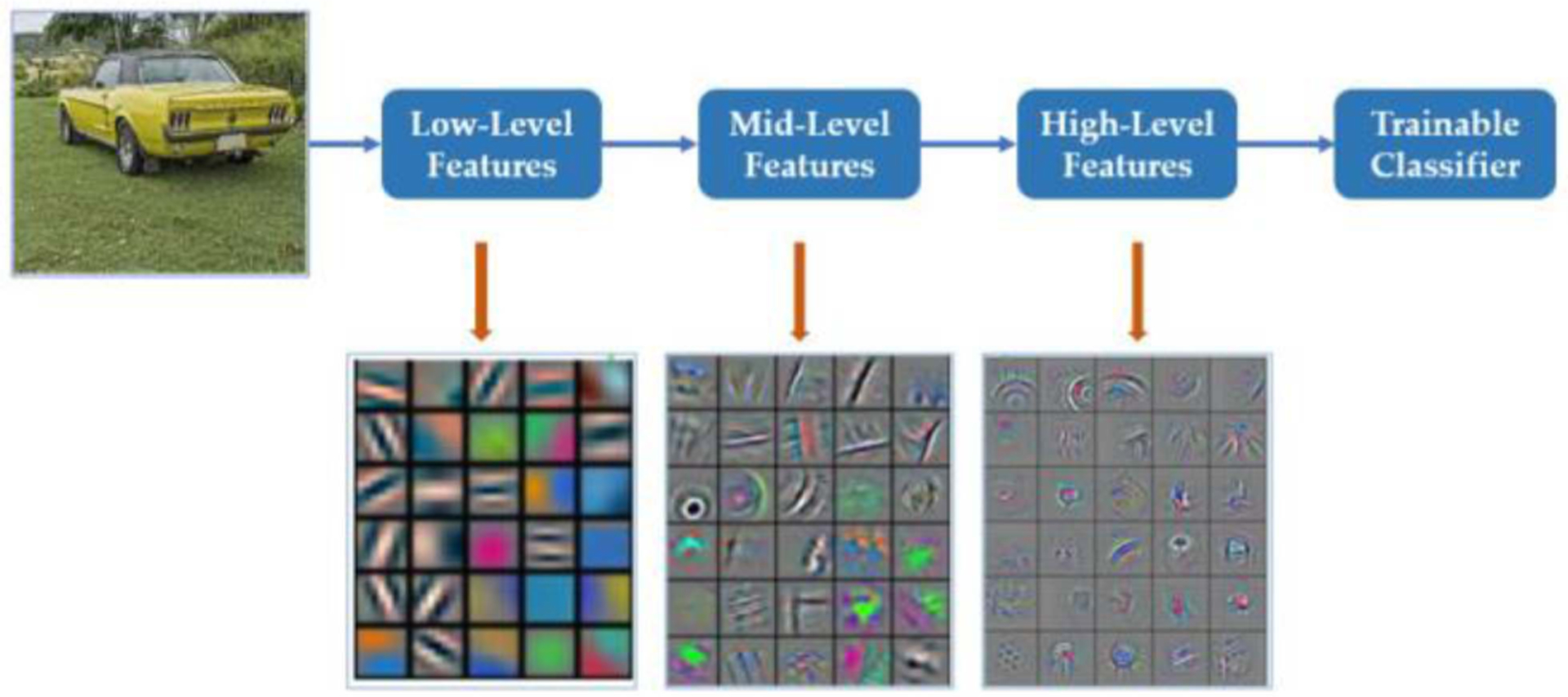
Depiction of different model features reconstructed from different layers of a CNN. *From F. Meng, X. Wang, F. Shao, D. Wang, and X. Hua, “Energy-Efficient Gabor Kernels in Neural Networks With Genetic Algorithm Training Method,” Electronics, vol. 8, no. 1, Art. no. 1, Jan. 2019, doi: 10.3390/electronics8010105. Meng et al. is an open-access article distributed under the terms of the Creative Commons CCBY license and no changes were made to this figure.
Three factors play an important role in the learning process of a CNN, including sparse interactions, parameter sharing, and equivariant representations [37], which make CNNs computationally efficient. Sparse interactions are also called sparse connectivity. It means each neuron is connected to only a limited number of other adjacent neurons instead of full neurons in the next layer, which requires fewer calculations to obtain the output. Parameter sharing refers to the fact that each kernel is location invariant between input images, aiming at controlling the number of parameters. Moreover, the parameter sharing property makes the convolutional layer equivariant to translation. Take object detection as an example. No matter where the object is, it can be detected and recognized because the kernel is the same for different parts of the whole image. Though these three methods are basic, they contribute significantly to improving the efficiency of a neural network.
2). Pooling Layer:
Pooling layers are also widely used in CNNs. This layer is designed for compressing the feature map to simplify the network computation and get the main feature of each feature map. Thus, the size of the images becomes smaller after the pooling layer. Similar to the convolutional layer, the stride, padding, and dilation concepts exist in the pooling layer as well. The relationship between the input size and the output size of the pooling layer is the same as (12).
There are two main kinds of pooling methods: 1) max pooling [38] and 2) average pooling. As Fig. 2(b) shows, for the max-pooling method, the maximum of each filter will be kept, while the average value of each activation will be computed and kept for the average pooling method. In practice, neither of the two methods appear to have advantages over the other.
3). Upsampling Layer:
In applications of segmentation [33] and synthesis [39], upsampling layers are deployed for extending compressed features to details in output images. To expand the image size, one of the simplest ways is to use interpolation, including nearest, linear, bilinear, trilinear, or bicubic resampling. Another approach is to reverse the concept of max pooling [40]. During the unpooling procedure, the locations of maximums in each filter will be filled into the larger zero-filled matrix according to location. This tracks the locations of the strongest activations so that it can reconstruct detailed features of an object [41]. Another approach is the dilated convolution [42]. This dilation convolution layer with dilation less than one, adds zero between input pixels and perform convolutions. The advantages of dilation convolution are extending receptive fields at no sacrifice of resolution. The unpooling layer and dilation convolution layers are shown in Fig. 2(d).
4). Activation Layer:
Activation functions are designed for increasing the nonlinear property of neural networks so that the neural network can approach the real map between the input and output as much as possible. Without the nonlinear activation functions, the neural network cannot solve the “exclusive or” (xor) problem. In recent years, more and more activation layers have been put forward.
For the sigmoid activation function, no matter what the input value is, the output will be limited in the range from 0 to 1, which can be thought of as the probability and is helpful to explain the result meaning. It is widely used for binary classification problems by comparing the output with the threshold, which is usually set as 0.5. The output larger than 0.5 can be labeled as one class while that smaller than 0.5 can be labeled as another class. However, it also has some problems. First is the gradient vanishing problem. According to the deviation function of sigmoid, the gradient is almost zero when the input is larger than 10 or smaller than −10. This means the weight of such kind of neurons will not be updated during the backpropagation. As a result, the neuron cannot learn from the data, and the neural network cannot be optimized. Second, the nonzero-centered problem. The output of the sigmoid function ranges from 0 to 1, which requires more time to converge because the inputs for the next layer are all positive, and thus the gradients for all the neurons are in the same direction. This could introduce undesirable fluctuations during training. Third, the sigmoid function can be computationally time consuming because exponentiation computation is involved.
The tanh function and sigmoid function are very similar. They are both smooth and easy to compute the derivative function. The tanh function also has the vanishing gradient problem and the exponentiation computation problem. However, the tanh function output ranges from 1 to −1, so the tanh function solves the nonzero-centered problem.
The ReLU activation function [43] is widely used successfully in many applications. It is defined as follows: Compared with other activation functions, the ReLU function alleviates the vanishing gradient problem to some degree. This is because, in the positive interval, the output of the derivative function can never be zero. Moreover, it is much faster to do the computation since it only needs to make the comparison with zero according to the formula. Finally, it can accelerate the process of convergence significantly as well. However, some limitations still exist. For example, the output of the ReLU function is also nonzero-centered. As a consequence, there could be some dead neurons due to the zero gradient when the input is negative. Dead neurons imply that some neurons can never be activated, so their weights can never be updated. To deal with the dead neuron problem some improvements have been suggested, such as the Leaky ReLU, ELU [44], and PReLU [45] functions, which allow a very small gradient in the negative interval. However, there is no strong evidence that the leaky ReLU and ELU functions will always work better than the ReLU function.
5). Batch Normalization Layer:
Batch normalization [46] was introduced by Ioffe and Szegedy in 2015. It is usually placed between the convolutional layer and the activation layer and is used to normalize the output of the convolutional layer. The details are shown in Fig. 2(c). A batch of data, x1, x2, and x3 are the inputs of the convolutional layer. z1, z2, and z3 are the outputs of the convolutional layer. Based on these outputs, the mean μ and standard deviation σ can be computed through the following formula:
| (13) |
| (14) |
Then, the normalized one can be computed like this one
| (15) |
After (15) is applied, the data distribution becomes stable with the average equaling zero and standard deviation equaling one. However, such simple normalization for the input of a layer may affect the layer’s nonlinearity. For example, if sigmoid is chosen as the activation layer, this normalization will force its inputs to be in the linear region, which reduces the nonlinearity. Therefore, two other parameters, γ and β, are introduced and an additional transformation is added to (15) just as (16) shows. γ and β are learned by the network during training and are used to shift the distribution of the data, so the nonlinearity of the network can be restored
| (16) |
Since the input of the activation layer has been processed into a certain range, this can reduce the likelihood of neurons getting into a saturated state. For example, if the sigmoid activation function is used and the input of the activation layer has been transferred into the range from −10 to 10, then the derivation function of the sigmoid can hardly become zero. As a result, the neurons can keep learning and update their weights. Additionally, batch normalization can also improve the training speed, performance, and stability of neural networks because it allows each layer of the neural network to learn by itself a little bit more independently of other layers. As a result, it is easier for the neural network to learn and converge.
6). Dropout Layer:
The dropout layer [47] is designed for solving the overfitting problem. Overfitting occurs when the model performs very well on the training dataset but performs badly on the validation dataset. This problem is often caused by smaller training datasets compared with the number of parameters of the model. Since the problem is related to the number of parameters, the dropout layer tries to ignore half of the neurons in a single layer randomly during the training, as shown in Fig. 2(e). In this way, the dependency between neurons in adjacent layers is weakened. As a result, neurons are forced to function more independently instead of depending on other neurons.
7). Fully Connected Layer:
In CNNs, fully connected layers are commonly used in the last few layers of a CNN. They map the feature learned in the previous layers to the marked sample space. The first fully connected layer can convert a multidimensional feature map into a 1-D vector through the convolution operation. During the conversion, the kernel has the same size as the feature map, which means the same height, the same width, and the same depth. An activation function usually follows the first fully connected layer, and its output is the input of another fully connected layer. Similar to neurons in the MLP, the neurons in the fully connected layer are connected to each neuron in the previous activation layer, while the neurons in the same layer are independent.
In other neural networks, like the AUTOMAP DL network used for medical image reconstruction [48], fully connected layers can be used at any layer. However, just as introduced above, neurons in the fully connected layer will be connected to those in the previous layer, which means a huge number of model parameters are needed. In practice, it is hard to train a network with so many parameters due to both computing hardware limitations and challenges with the convergence of extremely large models.
8). Infinite Possibilities:
In addition to the single layers introduced above, some other operations can also happen between nonadjacent layers, like addition, subtraction, multiplication, and concatenation. These layers allow the outputs from different layers to do some computation and make the design of the model more flexible. DL network layers can consist of any programmable operation.
III. Overview of Deep Learning Applications in Medical Imaging
Artificial neural networks evolved from the field of computer vision and have been successfully applied to solve a wide range of problems within the medical imaging field. Specifically, the utilization of DL in this area is greatly motivated by the fact that methods depend on the data, and no previous knowledge of it is required [49]. As a result of this attribute and the uncertain nature of most medical imaging data, DL has become an excellent alternative to solve common problems in the field. Classification, regression, segmentation, and image synthesis and denoising are among the most common DL applications employed to address medical imaging challenges, such as disease detection and prognosis, automatic tumors detection, and image reconstruction. Moreover, the DL model architecture depends on the specific application and in this section. We will attempt to summarize the current literature containing various challenges in the medical imaging field and DL models that have been used to address them.
A. Classification and Regression
Image classification and regression are DL applications that share many network architecture features but are used to solve distinct types of medical imaging problems. The objective of classification is to sort input images into two or more discrete classes, such as to detect the presence or absence of disease. Meanwhile, image regression is concerned with providing a single continuously valued output from an image input, such as a clinically relevant score. For both applications, the network is required to have an input layer, followed by a fixed number of hidden layers and an output layer. Conventionally there is a decrease in the number of filters or nodes as we move deeper into the network. A DL model used for image classification could be transformed into a regression model by simply modifying the activation function of its final output layer. For a binary and multiclass, multilabel classification, a sigmoid activation layer is utilized, while a SoftMax activation is used for multiclass-single-label classifiers [50]. In the case of regression, a linear activation is required for continuous output, and a sigmoid one for values between 0 and 1 [50]. Moreover, DL networks can be utilized to extract high-level features from data that are later inputted into a common ML model, such as a support vector machine (SVM) or Bayesian network (discussed in Section V), to perform the classification or regression task.
Currently, DL classifiers and PET data have been broadly used within the neuroimaging field for the early detection of Alzheimer’s (AD), specifically within the mild cognitive impartment (MCI) phase, and Parkinson’s (PD) disease. Several studies have performed AD/MCI classification using a combination of common ML techniques with DL methods. Unsupervised DL networks, such as stacked autoencoder (SAE) [51], [52], Boltzmann machine (DBM) [53], and DBN [54], were applied to extract high nonlinear features or patterns from PET and magnetic resonance imaging (MRI) data that were then inputted into an SVM classifier. Other studies utilized variants of deep multitask learning networks for feature selection in AD/MCI diagnosis [55], [56]. Furthermore, CNNs have been used for AD/MCI detection. PET image patches were inputted into a 2-D CNN network to explore the effect of multiscale data individually [57] and combined with multimodal data [58] on the early diagnosis of AD. A CNN network was used to predict cognitive decline in MCI patients (development of AD) [59]. Moreover, 3-D patches from PET images demonstrated to be more effective than MRI patches when using a 3-D CNN network or AD/MCI diagnosis [60]. Another way of including 3-D information into a DL classifier is by using 2-D image slices in different directions; Liu et al. included 3-D information into a classifier by inputting PET image slices of the brain in the axial, sagittal, and coral directions into a DL network composed of convolutional and recurrent neural layers [61]. Moreover, the feasibility of amyloid PET images for early detection of AD was studied by training a 2-D CNN network using amyloid positive and negative cases and testing it on equivocal cases [62]—a 3-D CNN was applied by combining amyloid PET with structural MRI data [63]. Multimodal hippocampal region of interest (ROI) images were applied to a 3-D VGG variant network for AD/MCI classification [64]. Finally, PET and single-photon emission computed tomography (SPECT) data along with CNN networks and LASSO sparse DBN have been utilized to detect neurological disorders, such as Parkinson’s disease [65], [66] and brain abnormalities [67].
DL-based classifiers have also proven to be beneficial within the cardiac and oncological imaging fields. Within the cardiac imaging field, a DL model (composed of convolutional and fully connected layers) and SPECT myocardial perfusion imaging were used to predict the presence of obstructive coronary artery disease [68]. Additionally, a pretrained Inception-v3 network [69] was utilized to extract high-level features from polar maps that following feature selection was then inputted to an SVM model to classify between cardiac sarcoidosis (CS) and non-CS [70]. Meanwhile, in the oncology field, PET data and CNN networks were used to predict treatment response in esophageal cancer patients after neoadjuvant chemotherapy [71] and radio-chemotherapy [72] and in chemoradiotherapy treated cervical cancer patients [73]. Additionally, a Bayesian network has been used to explore the biophysical relationships influencing tumor response and to predict local control in lung cancer using dosimetric, biological, and radiomics data [74]. For more information regarding DL methods for image radiomics, please see the following [75]. CNN networks were also used to detect mediastinal lymph node metastasis [76] and define T-stage of lung cancer [77]. An automatic classification system to detect metastasis on bones was created using artificial neural networks, and its performance was compared with eight other ML methods, such as SVM [78]. Furthermore, multimodal imaging data and a residual network (RN) were utilized to detect the molecular subtype of lower-grade gliomas tumors in the brain [79].
DL-based regression models are commonly applied to predict risk factors or treatment prognosis but could also be used to improve image quality. Ithapu et al. [80] explored the feasibility of an AD biomarker obtained from a randomized denoising autoencoder (AE) to filter out low-risk subjects from the MCI population and consequently reduce the sample size and variance requirements for clinical trials testing possible treatments for AD. The network predicted a risk factor (value between 0 and 1) to predicted how close an MCI patient was to develop AD [80]. Another study, successfully inputted gray and white matter volumetric maps and raw T1 MRI images to a 3-D CNN network to predict age [81]. PET data from normal subjects and a variational AE were used to determine how far from normality a brain was by predicting an abnormality score; the model was trained to learn the brain structure of normal subjects [82]. Unenhanced computed tomography (CT) images were used to predict SUV maximum value from lymph nodes as a surrogate endpoint for malignancy by applying a 3-D CNN network [83]. The 3-D CNN network architecture has also been used to predict survival risk prior to treatment from PET/CT images from rectal cancer patients [84]. Finally, a proof-of-concept study showed that CNN networks can be used to improve the timing resolution for time-of-flight PET utilizing a simple detector setup [85].
B. Segmentation and Image Synthesis
DL networks are currently implemented for medical image segmentation and synthesis. Image segmentation can be performed by assigning a class label to each individual pixel (semantic segmentation) or by delineating specific entities like tumors and lesions (instance segmentation). Moreover, the objective of image synthesis is to obtain a desired/unavailable image from an available/distinct one. With regards to the network architecture, both applications may be performed by applying some variant of the typical encoder–decoder architecture, often realized as a “U-Net” [33]. In the U-Net architecture, the input image size is downsampled during the encoder layers and then upsampled in the decoder layers—providing a continuous voxel-wise mapping from the input.
DL networks are commonly used to segment anatomical areas and detect tumors or lesions. Hu et al. utilized a 3-D CNN network to conduct a semiautomated segmentation of the liver by learning subject-specific probability maps from CT images [86]. A generative adversarial network (GAN) network was trained to segment white matter from only brain PET images [87]. For tumor segmentation, a 3-D U-Net CNN network was trained to automatically detect and segment brain lesions on PET images with a 0.88 and 0.99 specificity at the voxel level [88]. PET/CT image slices were inputted into a 2-D DL network for malignant gross tumor volume segmentation in the head and neck [89]. Meanwhile, Guo et al. [90] designed a 3-D DL network based on convolutional layers with dense connections for the same task. Zhao et al. [91] used a U-Net architecture to segment nasopharyngeal carcinoma tumors using PET/CT image slices. 3-D U-Net networks have also been combined with a feature fusion module [92] and graph cut base co-segmentation [93] for lung tumor segmentation from PET/CT images. The output was a single tumor mask for the first method and two (one from each imaging modality) for the second one. Another study designed a variant 3-D U-Net network architecture to segment lung tumors from PET/CT images—each input channel (individual U-Net network) shared complementary information in the decoder section with the other channel [94]. Likewise, a coarse U-Net and adversarial network have been used to segment extranodal natural killer/T cell lymphoma nasal cancer lesions [95] and the performance of a U-Net was compared to a W-Net [96] on segmenting multiple malignant bone lesions, both studies used PET/CT images [97]. Finally, Zhou and Chellappa applied a CNN network combined with prior knowledge (roundness and relative position) to segment cervical tumors in PET images [38]. Regarding multimodal-based segmentation, Guo et al. explored the performance of three algorithmic architectures to integrate multimodal data when implemented as part of a segmentation system. MRI, PET, and CT images were used to train a CNN network to segment lesions of soft tissue sarcomas and showed superior performance than networks trained on single-modal images [98].
Some current DL-based image synthesis applications include PET attenuation correction and image reconstruction. DL methods have been utilized for attenuation correction of PET images acquired during simultaneous PET/MRI scans. Hwang et al. trained a convolutional AE (CAE), U-Net, and a hybrid network of CAE and U-Net to synthesize a CT-derived brain μ-map from the maximum-likelihood reconstruction of activity and attenuation (MLAA) μ-map. The synthesized μ-map contained reduced crosstalk artifact and was less noisy and more uniform, which could improve time-of-flight PET attenuation correction [99]. A similar variant of the U-Net network was applied to synthesize whole-body CT μ-maps from MLAA-based simultaneous activity and attenuation maps, which identified bone structures more efficiently [100]. Liu et al. [101] designed a DL-based pipeline for MRI imaging-based attenuation correction for PET/MRI imaging. In this study, a CAE network was successfully trained to generate a discrete-valued pseudo-CT brain scans using structural MRI images and applied the generated pseudo-CT scans to reconstruct PET images [101]. Likewise, a data-driven DL-based pipeline, known as “deepAC,” was created to perform PET attenuation correction without anatomical imaging by synthesizing a continuously valued pseudo-CT brain image from PET data [102]. Pseudo-CT brain images were also synthesized from structural MRI images using a DL adversarial semantic structure, which incorporates semantic structure learning and GAN from PET attenuation correction, and its performance was compared with atlas-based approaches [103]. A population in which atlas-based approaches for attenuation correction are likely to fail is the pediatric one—because most of the available atlases are created using data from adult subjects [104]. For that reason, Ladefoged et al. [105] explored the feasibility of a modified version of a UNet network to synthesize attenuation maps from PET/MRI data in pediatric brain tumor patients. Additionally, a Dixon volumetric interpolated breath-hold examination (Dixon-VIBE) DL network (DIVIDE) that uses standard Dixon-VIBE images (in-phase and out-of-phase and water 2-D Dixon slices) was trained to synthesize pseudo-CT maps for PET attenuation correction in the pelvis, introducing less bias than the gold standard CT-based approach [106]. Finally, a 3-D GAN with discriminative and cycle-consistency loss was proposed by Gong et al. to derive continuous attenuation correction maps from Dixon MRI images; the technique generated better pseudo-CT images than the segmentation and atlas methods and its performance was comparable to a CNN-based one [107]. For a detailed overview of DL approaches for attenuation correction in PET, please refer to the following review article [108].
With regards to image reconstruction, AUTOMAP, a DL-based framework was designed to reconstruct medical images from any modality using the raw data by mapping sensor to image domains [48]. Similarly, DeepPET, a DL-based pipeline was created to reconstruct quantitative PET images from its sinogram data, which created less noisy and sharper images [109]. Furthermore, a stacked sparse AE was used for dynamic PET imaging reconstruction and compared its performance with conventional methods, such as maximum-likelihood expectation maximization (MLEM)—it effectively smooths and suppresses and recovers more details in the edges and complex areas [110]. Another study utilized a CNN network to synthesize patient-specific nuclear transmission data from T1 structural MRI data and evaluated the synthesized data on the reconstruction of both static and dynamic PET brain images [111]. DL networks have also been used to synthesize PET brain images from T1 MRI ones [112] and vice versa [113], which may be useful when one of the image scans is not available. Likewise, a CNN network was used to predict 15O-water PET CBF images using single- and multi-delay arterial spin labeling and MRI structural images [114]. Additionally, a sketcher-refiner GAN network with adversarial loss function was trained to predict PET-derived myelin content map from MRI magnetization transfer ratio map and three measures derived from diffusion tensor imaging (DTI) [115]. Please refer to Reader et al. for a complete review of PET image reconstruction using DL approaches [116]. Finally, Shao et al. [117] utilized DL approaches to reconstruct SPECT images directly from projection data and the corresponding attenuation map. The proposed network utilized two fully connected layers for basic profile reconstructed followed by a 2-D convolutional layer where the attenuation map was used to compensate and optimize the reconstructed image—this method proved to be robust to noise [117].
C. Image Denoising and Super-Resolution Tasks
DL methods are also used for image denoising and super-resolution applications. The objective of image denoising is to obtain a ground truth from a noisy image. A residual encoder–decoder was first used to denoise CT images, where the noise was added to the images to simulate a low-dose CT scan [39]. Shortly after, Shan et al. [118] introduced a conveying path-based convolutional encoder–decoder (CPCE) network for low-dose CT denoising using both real and simulated (added noise) data. The novelty of this approach lies on the transfer learning feature in which a 3-D-CPCE network was initiated using a trained 2-D one, achieving better denoising results than training from scratch [118]. To better preserve structural and textural information, Yang et al. proposed a CT denoising method based on GAN with Wasserstein distance and perceptual similarity (WGAN-VGG) [119]. The WGAN-VGG network solved the oversmoothing problem observed in other approaches, reduced noise, and improved lesion detection by increasing contrast when applied on simulated quarter-dose CT images [119]. Meanwhile, You et al. [120] implemented a 3-D GAN using a novel structurally sensitive loss function (SMGAN-3D) to also address the oversmoothing problem when denoising simulated quarter-dose CT images. The structurally sensitive loss function is a hybrid that integrate the best characteristics of mean and feature-based methods, thus, allowing noise and artifacts suppression while preserving structure and texture [120]. Furthermore, noise2noise (N2N) methods have also been propose to denoise low-dose CT images; N2N methods reduce noise using pairs of noisy images [121]. Hasan et al. [121] explored the potential collaboration between N2N generators for denoising of CT images by processing images from a phantom, and showed that these collaborative generators outperformed the common N2N method. For denoising of single-channel CT images, an unsupervised learning approach known as REDAEP was introduced by Zhang et al. in which variable-augmented denoising AEs were used to train higher-dimensional prior for the iterative reconstruction—this technique was tested using simulated and real data [122]. Finally, the use of a deep CNN has been explored to denoise either/both low-dose CT perfusion raw data and maps using digital brain perfusion phantoms and real images [123]. The results demonstrated the network has a superior performance when applying it in the derived map domain [123]. Moreover, DL networks are used to denoise low-dose PET images to obtain high-quality scans that would only be available by applying a standard dose of radioactive. Xiang et al. [124] input real low-dose PET (25% dose) and T1 MRI images into a deep auto-context CNN network to predict standard-dose PET images. Similarly, Wang et al. [125] utilized a locality adaptive multimodality GANs (LA-GANs) to also synthesize high-quality PET images from low-dose PET and T1 MRI images alone or combined with DTI [126]. Meanwhile, Chen et al. [127] utilized simultaneously acquired MR images and simulated ultralow-dose PET images to synthesize full-dose amyloid PET images using an encoder–decoder CNN. Using computer-simulated data of the brain and lungs, Gong et al. [128] pretrained a residual deep neural network architecture to denoise PET images and fine-tuned it using real data—this method outperformed the traditional Gaussian filtering method.
Meanwhile, super-resolution applications are concerned with obtaining a high-resolution image from a low-resolution one. For example, Li et al. [129] applied a semi-couple dictionary learning (SCDL) technique, an automatic feature learning method, to improve the resolution of 3-D high resolution peripheral quantitative CT (HR-pQCT). The authors of this study applied a 2.5-D strategy to extract high- and low-resolution dictionaries from coronal, sagittal, and axial directions separately and obtained a superior performance compared with other methods, such as total variation regularization [129]. Additionally, an unsupervised super-resolution method based on dual GAN networks was introduced by Song et al. [130] to improve the resolution of PET images. This method eased the need for paired training inputs (low- and high-resolution images) by utilizing low-resolution PET and high-resolution MRI images, along with spatial coordinates—making the technique more practical as it is difficult to obtain ground-truth data on a clinical setting [130].
IV. Training Neural Networks
In this section, we define key steps necessary to implement a supervised DL application (Fig. 4). The steps as detailed below are data collection and preparation, network selection, network training and validation, and network testing and deployment.
Fig. 4.
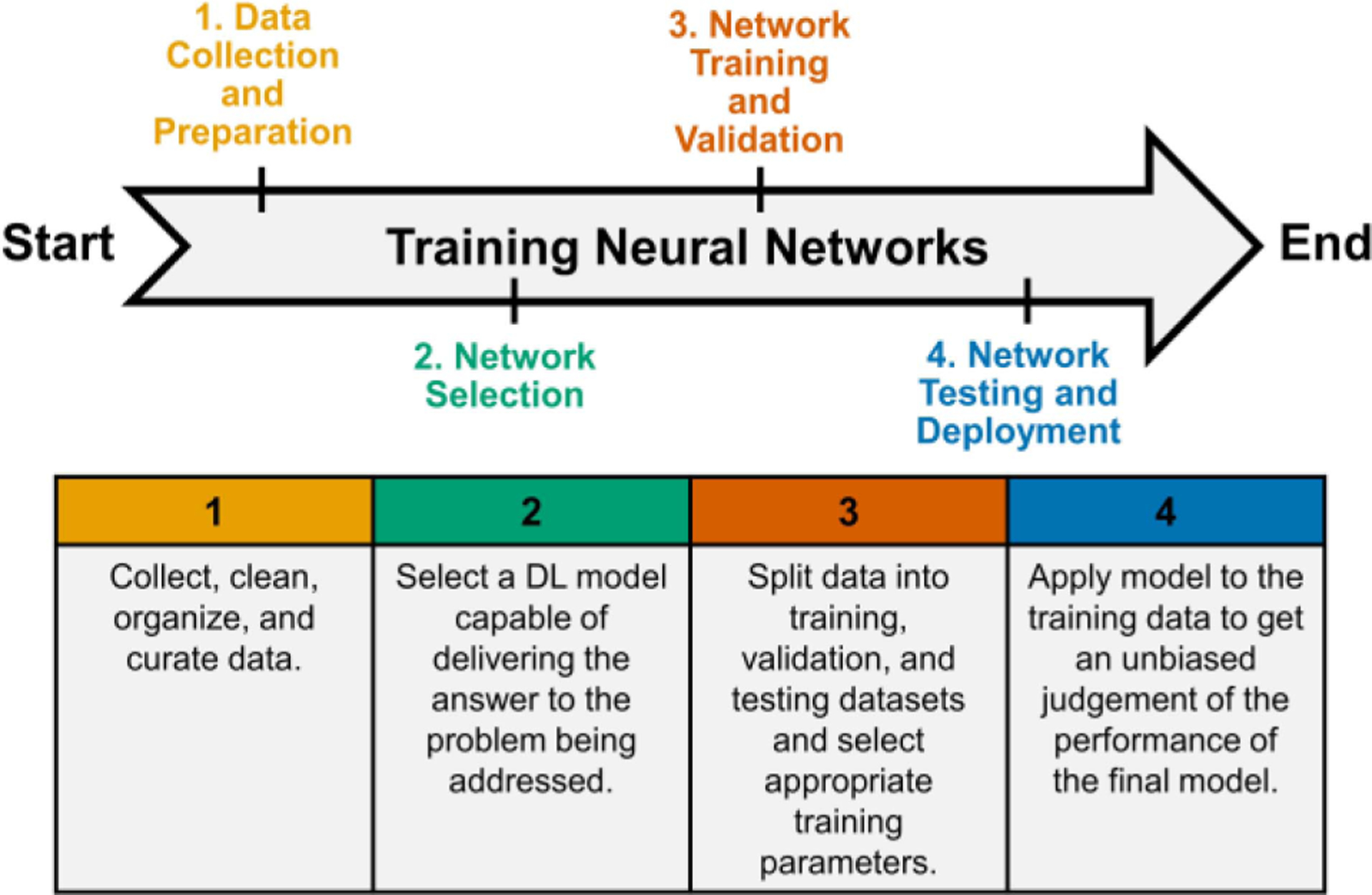
Overview of steps necessary to implement a supervised DL application. The first step is concerned with data collection and preparation; the dataset should only contain true negative and true positive cases. The second step is to select a network architecture to perform the task at hand. The third and fourth steps include the training, validation, testing, and deployment of the final model.
A. Data Collection and Preparation
The data utilized when implementing a DL method could be acquired at the study site to address the research question at hand or obtained from a public medical imaging database. The objective of public medical imaging databases is to enhance the understanding of diseases by providing the scientific community with fair access to large quantities of high-quality imaging data. Examples of well-known public medical imaging databases are the Alzheimer’s Disease Neuroimaging Initiative (ADNI) [131] and the Cancer Imaging Archive (TCIA) [132]. The ADNI database provides MRI and PET images, genetics, cognitive tests, cerebrospinal fluid, and blood biomarkers with the goal of improving the characterization of the Alzheimer disease [131]. Meanwhile, TCIA hosts multimodal images of cancer and allows scientist to publish new datasets after approval [132].
The data preparation step is often the most time-consuming part of the DL network training process. The purpose of this step is to clean, organize, and curate the data in a way that is useful for the task at hand and accessible for reproducibility and sharing purposes. The first step is to make sure the dataset only contains true negative and true positive cases, in other words, a good quality ground truth. For example, when training a DL network for brain tumor detection, images containing other lesions, such as hematoma and infections should not be included. Additionally, images should be normalized to alleviate any error due to acquisition from various scanners/protocols. The images should all be saved using the same format and have the same size, resolution, and pixel scale. The only difference between images should be those features related to the problem the DL network will be trained to solve. During the data acquisition process, methods to alleviate hidden bias are discussed in Section V.
B. Network Selection
After data preparation, a DL model structured to deliver the answer to the problem being addressed should be selected. Currently, deep FNNs are the most common type of DL networks applied to solve medical imaging problems. FNNs are characterized for having information movement in only one direction (no feedback) and usually contain an input layer, one or more hidden layers, and an output layer. In addition, in FNN networks, each unit of one layer is connected to every unit on the next one, and there is no connection between neurons in the same layer. In this section, we will present the FNN model architectures commonly applied within the medical imaging field.
1). Feedforward Neural Network:
CNN: A CNN is a DL model capable of detecting spatial and temporal high-level features from inputted images. The key component of CNNs is convolutional layers which work by convolving filters with input images that assign ranked weights and biases to individual features differentiate one from the other [133]. The example of well-known CNN architectures is LeNet-5 [24], AlexNet [26], ZFNet [40], GoogleLeNet/Inception [28], VGGNet [27], and U-Net [33].
RN: An RN is a DL model characterized by having connections between the output of previous layers to the output of new layers [134]. Like CNNs, RNs can detect high-level features from images. For example, an RN could have a connection from the output of layer 1 to the input and output of layer 2. The example of the RN architecture is ResNet [134] and DenseNet [135].
AE: An AE is a neural network capable of performing dimensionality/feature reduction by learning/encoding features from a given dataset [136]. Examples of AE architectures are sparse [137] and variational [138] AEs.
GAN: A GAN is a DL model capable of synthesizing entirely new data by having a generative and discriminative network working together/against each other [139]. The objective of the generative network is to create artificial data from the distribution space of the input dataset [139]. Meanwhile, the discriminative network attempts to discriminate between the artificial and real data [139]. As a result, the generative network is trained to increase the error rate of the discriminative one by creating a more realistic data [139].
Restricted Boltzmann Machine (RBM): An RBM is a stochastic DL model that learns the probability distribution of the input dataset [140]. This type of network is characterized by having one visible layer and one hidden layer (there is no output layer), and every unit in the visible layer is connected to every unit within the hidden layer, but there is no connection between units/nodes in the same layer [140]. Examples of the RBM-based architectures are the deep belief network [141] which contains stacked RBMs and the deep Boltzmann machine [142].
C. Network Training and Validation
1). Train, Validate, and Split:
Before the start of training, the data need to be divided into three parts, including the training dataset, the validation dataset, and the test dataset. In the training phase, only a training dataset and a validation dataset are needed. A testing dataset can only be used after model training has been finished. Ripley [143] defined the training set, validation set, and test set as follows:
“– Training set: A set of examples used for learning, that is to fit the parameters of the classifier.
– Validation set: A set of examples used to tune the parameters of a classifier, for example to choose the number of hidden units in a neural network.
– Test set: A set of examples used only to assess the performance of a fully specified classifier.”
The training dataset is used to fit the model, and the model mainly learns from this data directly. The validation dataset aims at providing an unbiased evaluation of a model fit on the training dataset. The evaluation contributes to tuning hyperparameters which are set manually before training, like the depth of the model, the training batch size, loss functions, and optimizers introduced in the following part, to help the model get improved. If the model is improved, its performance on the validation dataset can be improved as well. Therefore, the validation dataset affects the model indirectly. In a word, the training dataset and validation dataset are involved in the training. The training dataset is used for training the model directly while the validation dataset is indirect.
However, what strategies are best to split the dataset? Usually, the ratio between the training dataset and the validation dataset size is 8:2 or 7:3. It is a general method for splitting. Actually, the real split ratio is affected by the volume of the whole dataset and the number of parameters of the actual model. If the dataset is very large when compared with the model’s parameters, the proportion between training and validation has fewer effects on the training result because either the training data volume or the validation data volume is large enough to train the model or give an accurate evaluation of the model’s performance. However, if the dataset is small, the split ratio should be considered carefully. For the model with few hyperparameters, it is easy to validate and tune the hyperparameters to make the model perform better, so the size of the validation dataset can be reduced under this circumstance; on the contrary, if the model is complex and has many hyperparameters, the proportion of the validation dataset should be increased. In summary, the train–validation split is quite specific to the volume of the dataset and the complexity of the chosen model.
In addition, class imbalance needs to be considered carefully during data splitting. For example, consider the situation where negative examples take up 90% of the database while the positive ones only consist of 10%. Under such circumstances, it is not suitable to use 0.5 as threshold and refer to the accuracy as the indicator of a model’s performance because in this way the model can always give its prediction as the negative one no matter what the input is, yet the accuracy is still 90%.
Several simple methods have been proposed to solve this problem, including undersampling, oversampling, and threshold moving. Undersampling is to delete some data from the majority class while oversampling is to duplicate the data from the minority class. However, these two methods can change the data distribution obviously. Undersampling wastes precious data, and oversampling can lead to overfitting. Compared with these two methods, moving the threshold is often a better choice. The new threshold should be the minority ratio to the total. The evaluation method should also be modified, such as using the receiver operating characteristic curve analysis.
However, the methods mentioned above cannot get an accurate estimation of the model, since the validation results fluctuate significantly due to different split between the training dataset and the validation dataset [144]. Cross-validation is frequently used to solve this problem. Among various kinds of cross-validation methods, k-fold cross-validation is the most commonly used one. The first step is to choose the single parameter for this method, k, which refers to the number of groups a given dataset should be split into. Kohavi [145] suggested that tenfold cross-validation is sufficient for model selection even if computation power allows using more folds. The second step is to divide the dataset into k groups. Then k − 1 groups can be selected as the training dataset and one group as the validation dataset. There should be k different selections. Finally, train the model with the training dataset. As a result, k different models obtained for which model performance can be assessed across cross-validated runs, and if necessary, the single best model performing model can be selected according to its performance on a corresponding validation dataset.
2). Loss Functions:
As described above, deep neural networks learn by means of a loss function. The goal of the model is to minimize the loss as much as possible, so loss functions play an important role in training the model. Take the classification problem as an example. If the prediction deviates too much from actual results, the loss function will become very large at first. However, with the help of an optimization function, the model can be improved, and the loss will go down. Different loss functions have been designed to solve different problems. Broadly, most problems can be seen as a regression problem or classification problem. In practice, any programmable function can be used as a loss function. Here, we highlight the most commonly utilized approaches.
In regression and image synthesis, a continuous value will be given. Three loss functions commonly used in solving this kind of problem: 1) mean-square error (MSE); 2) mean absolute error (MAE); and 3) Huber loss [146]. If m is the number of training samples, y(i) is the ground truth while f (x(i)) is the prediction of the model, the corresponding formula for each loss functions can be presented as follows.
- MSE:
(17) - MAE:
(18) - Huber Loss:
(19)
According to the above formulas, the MSE’s derivative is consecutive, while the MAE’s not. Additionally, the derivative of MSE changes, which helps the model converge while the derivative of MAE is nearly the same. However, when it comes to outliers, MSE is more sensitive, while MAE is more robust. That is because if ∣y(i) − f (x(i))∣ > 1, the loss from MSE will become much larger than the loss computed by MAE. Therefore, there is no assertion that any loss has definite advantages over the other one. In practice, it depends on the application. For example, if the sensitivity to outliers is very important, and they should be detected, then MSE should be a better choice for solving that problem.
However, under some circumstances, neither MSE nor MAE is suitable. For example, if the target of 90% of the training samples is 150 while that of the rest ranges from 0 to 30, the performances of MSE and MAE may not be suitable. For the MAE, it will ignore those outliers and give the same prediction, 150, all the time. For the MSE, it will be greatly affected by those outliers. As a result, it performs badly on most data. In order to make use of the benefits of MSE and MAE, the Huber loss is proposed. Herein δ is a hyperparameter, which controls the definition of outliers. According to the formula, different measures are adopted for dealing with normal data and outliers, so the result performs better in general as long as the suitable value for δ has been chosen.
In classification and segmentation, the output of the model should be in a set of finite categorical values. The classification problem can be divided into a binary classification problem or a multiclass classification problem based on the number of categories. For example, when dealing with a single-digit recognition problem, the prediction of the model should be one of the numbers from 0 to 9. Since there are ten categories, it belongs to the multiclass classification problem. Binary cross-entropy is the recommended loss function for solving the binary classification problem, while multiclass cross-entropy loss is suggested for the multiclass classification problem.
The following formula shows how binary cross entropy loss is computed. m is the number of training samples. y(i) is the ground truth for the sample x(i) while p(i) is the prediction of the model, which means the possibility of the input belonging to a certain class
| (20) |
Similar to the binary cross entropy loss, m is the number of training samples. C is the number of categories. stands for the ground truth that the ith training sample belongs to the jth category or not while is the prediction from the model which means how likely the ith training sample belongs to the jth category
| (21) |
In addition to the basic loss functions introduced above, there are some other complex loss functions designed for some specific applications, like the perceptual loss function for style transfer [147]. Furthermore, custom loss functions can also be developed and used according to the specific problem.
3). Optimizers:
In the previous section, several loss functions have been introduced. However, the loss is just a static value between the estimated output and the desired output. How does the model improve this estimate during the training process? This is where optimizers come in. They tie together the loss function and model parameters by updating the model in response to the output of the loss function. In other words, optimizers learn from the loss function and update model parameters by following a certain rule. Gradient descent is the classic optimizer; however, other improved strategies have been proposed.
a). Gradient descent:
The rule for parameters update is shown as follows:
| (22) |
θ stands for the model’s parameters. η is the learning rate. is the gradient of loss function to parameters θ. In gradient descent, the loss is computed with the whole dataset, so the computed gradient is accurate. However, it is hard to add more data to update the model at the same time. Moreover, it can be very time consuming if the dataset is very large.
Besides the dataset limitation of gradient descent, the learning rate is a hyperparameter, which should be given in advance. The learning rate has significant effects on the outcome of training, so the value should be chosen carefully. Fig. 5 shows the impact of the learning rate. If the learning rate is too large, which means the weights change too fast, it may be hard for the model to converge to the optimal value. However, if the learning rate is too low, which means the weights are updated very little at each step, it may take a long time to train the model, and the model is more likely to converge on a local minimum. In summary, the learning rate plays an important role in the gradient descent algorithm, and it should be chosen carefully.
Fig. 5.
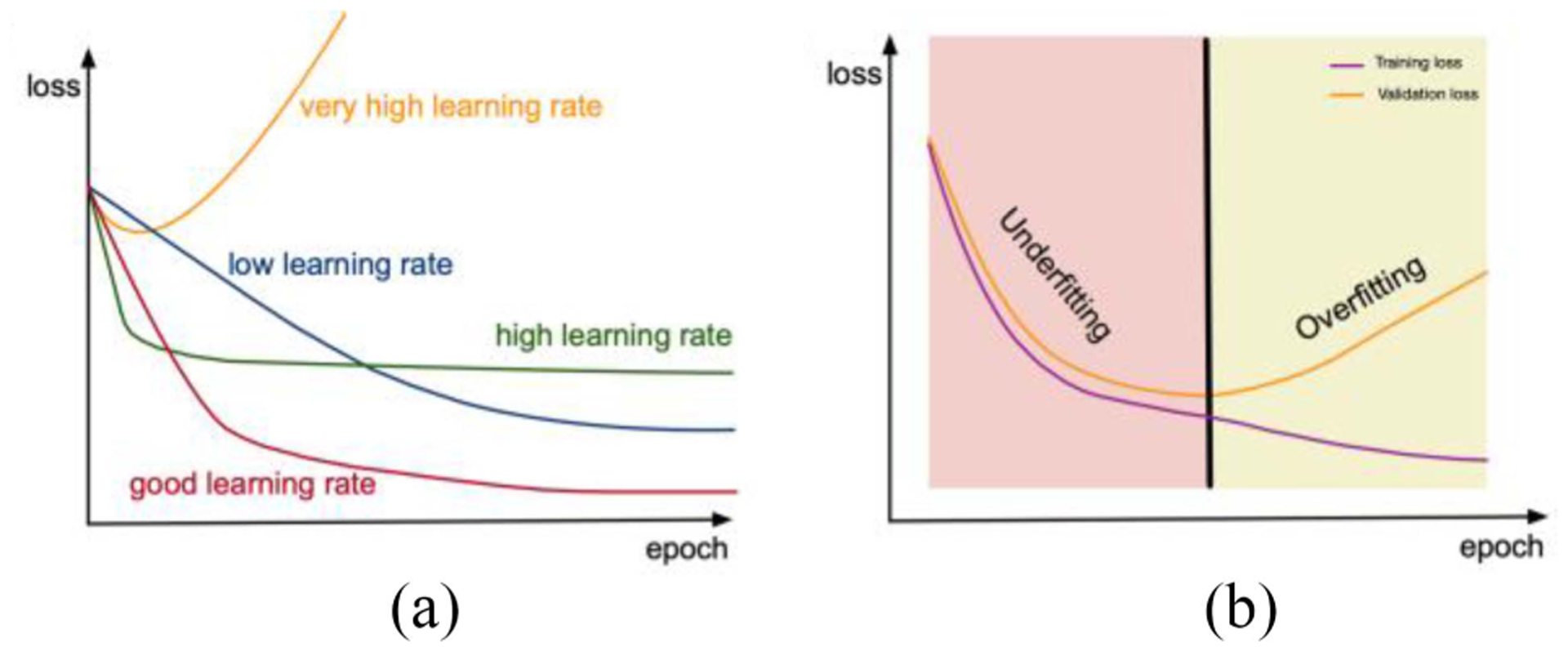
(a) Graphical depiction of training loss with varying learning rates. The optimal selection of learning rate can provide the lowest possible training loss. (b) Graphical depiction of training and validation loss. Overfitting can be observed when the validation loss increases while the training loss continues to decrease.
b). Stochastic gradient descent:
| (23) |
Since it is time consuming to compute the gradient with the whole dataset, it will save a lot of time if only one sample has been used. This is what stochastic gradient descent does. In this way, it is much quicker to train the model. However, the loss might fluctuate significantly. Additionally, since the gradient is not accurate, the model may converge on a local minimum, which may reduce accuracy compared with the gradient descent.
c). Mini-batch gradient descent:
| (24) |
Mini-batch gradient descent uses n samples to compute the gradient instead of only one. The standard deviation of updating parameters with mini-batch gradient descent can be reduced, and the final convergence is more stable as well.
However, this algorithm has two drawbacks. First, the mini-batch approach cannot guarantee optimal convergence. If the learning rate is too low, the loss will fluctuate around a minimum or even deviate. If the loss function is not convex, it is also easy to become stuck in the local minimum. Second, all parameters are updated with the same learning rate, which may not be reasonable. For features with lower frequency, the learning rate should be larger compared then for features with higher frequency. Moreover, the learning rate should become smaller and smaller with the increase of training epochs.
d). Momentum [148]:
To solve the aforementioned drawback, the concept of momentum has been introduced
| (25) |
| (26) |
γ vt−1 is the momentum. γ is often set as 0.9. After adding this term, the dimension in which the direction of gradient keeps the same changes faster while the one in which the direction of the gradient is not altered changes slowly, which could facilitate the convergence progress and reduce vibration. However, momentum is not smart enough to slow the update rate before the loss becomes larger.
e). Nesterov accelerated gradient [149]:
To make momentum smarter, the Nesterov accelerated gradient has been proposed
| (27) |
| (28) |
The future position θ − γ vt−1 is used to compute the gradient instead of the current position θ.
f). Adagrad [150]:
Adagrad aims at solving the second drawback of a mini-batch gradient algorithm, a constant learning rate
| (29) |
| (30) |
gt,i is the gradient of θi at time t, and it is the same as . here is a diagonal matrix where each diagonal element Gt,ii is the sum of the squares of the gradients with respect to θi up to time step t while ε is a smoothing term that avoids division by zero. η is the initial learning rate, which is often set as 0.01. According to the formula, the learning rate is low for those parameters which have been updated frequently. However, the denominator is an accumulated number, which will become larger and larger with the training going on. As a result, the learning rate will be very close to zero, which will lead to the end of training in advance. To solve this problem, RMSprop and Adadelta have been proposed.
g). RMSprop:
A very small learning rate can be caused by the accumulated sum, this problem can be solved by changing the accumulated sum term. Hinton proposed the following update rule:
| (31) |
| (32) |
η is recommended to be set as 0.001.
h). Adadelta [151]:
Adadelta is very similar to RMSprop in the first phase
| (33) |
| (34) |
| (35) |
However, η can be eliminated by using a similar idea, which means the initial learning rate is not needed any longer
| (36) |
| (37) |
As a result, the final form of the rule should be
| (38) |
| (39) |
i). Adam:
Adaptive moment estimation is another method that computes the adaptive learning rate for each parameter [152]. Combining the ideas from momentum and adadelta, it defines the decaying averages of past and past squared gradients mt and vt, respectively, as follows:
| (40) |
| (41) |
However, since mt and vt are initialized as the zero vector, it is easy for them to be biased toward zero at the beginning of the training. This can also happen when β1 and β2 are close to one. To avoid this problem, the following transformation is applied
| (42) |
| (43) |
Then, the update rule is listed as follows:
| (44) |
β1, β2, and ε are recommended to be set as 0.9, 0.999, and 10−8, respectively.
In summary, the classic optimizer is gradient descent; however, the computation involves the whole dataset. This is too time consuming, so stochastic gradient descent has been proposed. It is very fast and needs only one sample to update the parameters, but loss fluctuates significantly when using it. Therefore, mini-batch gradient descent was proposed. Still, two problems remained: 1) fluctuation around local minimums and 2) constant learning rate. To solve the fluctuation problem, the concept of momentum was proposed and improved with Nesterov accelerated gradient. Adaptive learning rate optimizers have been proposed as well, like Adagrad. The improvement of Adagrad for the problem of a vanishing learning rate has been suggested by RMSprop and Adadelta. Finally, Adam combines concepts from momentum and Adadelta.
There is no answer to the question of which is the best optimizer. It relies heavily on the data and problem. If the input data is sparse, the adaptive learning-rate methods are more likely to get the best results. For adaptive learning rate optimizers, like RMSprop, Adadelta, and Adam, are very similar and often do well in similar circumstances. Kingma and Ba [152] showed that its bias-correction helps Adam slightly outperform RMSprop toward the end of optimization as gradients become sparser. In general, both mini-batch SGD and Adam are widely utilized and perform well and are suggested to be utilized first.
4). Overfitting:
During the training process, several problems can occur. The most common one is overfitting. Overfitting occurs when the model fits very well on training data, but it does not generalize and perform well on the validation data. Several approaches can be applied to reduce the likelihood of overfitting in training DL models.
Getting More Training Data: If the training dataset is small, and the model is complex enough, the model may learn to remember the training data. However, after adding more data, the model will be forced to learn the underlying pattern from the training dataset instead of just remembering it. It is usually effective, but another problem is that sometimes it is hard to get more data in reality. Data augmentation discussed in Section V is also a strategy to reduce overfitting.
Regularization: In addition to enlarging the training dataset, adding a regularizer term to the loss function, such as the l1-norm and l2-norm, can be useful. This is because this term will become larger if the number of nonzero parameters of the model increases. As a result, the loss will become larger, which could hold back the overfitting process. Therefore, the regularizer term can also prevent the model from being too complex and help avoid the overfitting problem.
Early Stopping: Usually, if the training loss continues to decrease while the validation loss begins to increase, this is indicative of overfitting. Therefore, the training process should be stopped before the validation loss continues to increase. In this way, the generalization of the model can be maintained. Whether this method works or not depends on both the data and the model.
Adding Specific Layers: As described in Section II, the batch normalization layer and the dropout layer can help ease the overfitting problem. According to the batch normalization algorithm, the parameters μ and σ are computed with the batch data instead of the whole dataset. This can introduce some uncertainty, which can be helpful in avoiding overfitting. Additionally, a dropout layer can also deal with this problem. Since some of the neurons are chosen to be ignored in each layer, the model becomes simpler. As a result, it could help alleviate overfitting.
D. Network Testing and Deployment
Once the training of the model is finished, a test dataset is needed. The test dataset is designed to give an unbiased judgment of the final model for a certain task. Compared with the validation dataset, testing data can never affect the model’s training or performance, which means the model remains unchanged after testing. There are some key factors concerning the test dataset. First, there should not be any overlap among training, validation, and test datasets. This means the cases used for training and validation should not appear in the test dataset, otherwise, an assessment of the model’s generalization is incomplete. Additionally, test cases should cover not only a representative range of patient data as included in the training or validation dataset but also some edge cases which have not been seen by the model before but may exist in the real world. Where possible, the same type of input data but from other sources (different institutions) or systems (different vendors) should be tested to evaluate the model’s generalizability. Results from the test data can be used to test real-world model performance, including some important indicators, like MSE and accuracy. Then these indicators show the performance of a model and provide a way to compare the performances of different models. Once the model meets the minimum requirements for the specific application, it can be deployed. The model parameters and structure remain unchanged. It is key that the data used for training, validation, and testing are representative of data that are encountered during deployment.
V. Robustness
Advanced AI technology will deliver huge improvements to the healthcare industry only if AI-related products meet ethical and legal requirements. According to a recent discussion paper about Proposed Regulatory Framework for Modifications to AI/ML-Based Software as a Medical Device [153] presented by FDA and Code of Conduct for Data-Driven Health and Care Technology [154] presented by National Health Service of the United Kingdom (NHS), transparency and accountability are always valued. Is the trained model robust enough to various clinal situations? How can we prove it? It is a new challenge beyond simple training/validating processes.
A. Data Selection
The DL technology is also called the data-driven technology; thus, dataset selection is one of the key parts of the DL pipeline. As the data preparation and data split have been introduced above, the discussion here concentrates on avoiding structural bias, which is not only an ethical concern, but also related to performance after commissioning. The difference between the training datasets distribution and deploying datasets distribution (the datasets faced in the application) in the real world will lead to potential performance drop. Even in the same distribution, subsampled datasets will also cause instability. Additionally, imaging protocols can also be treated as a source of bias. The popular methods designed to diminish bias from datasets are as follows.
Larger dataset population.
Data augmentation.
Manual division of datasets.
Human investigation.
Deriving at the beginning of learning, Valiant [155] built the fundamental learning theory called probably approximate correct learning (PAC learning). The statement was proved via statistics that a larger training dataset would lead to a higher probability of less error. Hence, extending the training datasets is always the best way to improve accuracy for DL applications. However, huge amounts well-annotated data or even unlabeled medical data may be too expensive or time consuming to acquire.
B. Data Augmentation
Given limited data samples, it is intuitive to think of amplifying them for a larger dataset. The method is called data augmentation. In the medical imaging field, images often maintain one or several spatial invariance properties, including shift, shear, zoom, reflection, and rotation (i.e., spatial transformation does not change the diagnoses), researchers may choose manually implement those transformations to augment datasets. While some specific applications may violate partial invariance, generally, data augmentation can increase the dataset population as well as inject domain knowledge (spatial invariance properties) into DL models. In a review presented by Shorten and Khoshgoftaar [156] regarding data augmentation, those basic augmentation techniques can improve accuracy in traditional classification challenges. However, some techniques may not be suitable for medical images. Random cropping or image fusion could remove crucial diagnostical details. In medical image classification tasks, Hussain et al. [157] focused on the influences of differential techniques and proved those did improve task accuracy. It is also mentioned that adding noises (Gaussian and Jittering) and Gaussian blurring are also options to simulate perturbation and real-world artifacts encountered in imaging protocols.
As previously described, the dataset division focuses on how to divide collected datasets into training/validating/testing three subsets. If the validation loss is significantly different higher than the training loss, we encounter overfitting, indicating that the model learns too much from the training dataset at the sacrifice of generalization. From the dataset division view, one possible reason is imbalanced division. Perhaps some details or features emerge only in the validation datasets. Or the populations of categories are biased, shown as one category of data (one label in classification or one feature in synthesizing) occupies most data populations and squeezes computational resources of other categories. In this case, data from minor categories should be amplified to retrieve the balance among categories. After training, the same thing could happen during testing. Balanced dataset division may reduce the training loss, but it can be an appropriate way to maintain generalization for model deployment.
C. Ensemble Learning Methods
Ensemble learning is a DL training approach that can reduce the variance of predictions [158]. This method works by employing multiple DL networks simultaneously, instead of a single model, to perform the desired prediction [158]. There are two commonly implemented ensemble learning methods: 1) parallel ensembles and 2) cascade ensembles. Using a classification task as an example, “majority voting” is a commonly implemented approach for a parallel ensemble. When implementing a majority voting approach, an odd number of DL subnetworks are independently trained and evaluated individually by inputting the data in parallel. We see each subnetwork as an expert, and all experts vote for their prediction. The prediction with the most votes wins and is then output as the system’s prediction. If the subnetworks’ outputs are not binary, the final prediction may be obtained using a weighted sum of the individual subnetworks’ outputs. Additionally, as part of parallel ensemble two other techniques to fuse the information from each individual subnetwork include learning weights and dynamic classifier selection [159]–[161]. For the learning weights approach, a single network is trained to learn the optimal weights for each subnetwork. The dynamic classifier selection approach identifies the subnetworks offering superior performance near the interference point in feature space. In the cascade ensemble method, intermediate feature maps are processed step-by-step using several subnetworks organized as a pipeline. For example, a framework for cascaded U-net, including 3-D and 2-D U-net was built with the assumption that modifications to the simple U-net were not sufficient to improve performance and the cascaded framework could led to “a desired absence of overfitting” [162].
D. Generalization and Noise
Generalization is always a crucial part in data science, especially in deep learning [163]. In statistical theory, it is impossible to predict every possible case because we can only obtain our data by discrete sampling. Thus, there always exists a gap between the empirical, observed loss in the sampled population and the true loss from the full population. The outstanding performance of DL benefits from a huge amount of parameters, which leads to vulnerability due to overfitting, such that the model just “memorizes” the proper response to input data. So, when such a model is tested or applied to real-world data, the performance may drop.
Therefore, researchers are eager to find a solution to reduce overfitting and enhance the ability of generalization. Goodfellow et al. [37] stated that injecting noise into the train data could be recognized as a form of data augmentation. For a small dataset, noise in the input could make it harder for the model to simply memorize the training data, reducing generalization error. However, Zhang et al. [164] claimed and experimentally proved that DL models could easily fit random labels. due to the tremendous parameters of networks. Hence, noisy label in training data leads to poorer performance. Goldberger and Ben-Reuven [165] distinguished the clean label and error label using the estimation–maximization (EM) algorithm. It estimated the true label in the E-step and retrain the network in the M-step, repeatedly. Jiang et al. [166] designed a MentorNet, which taught a StudentNet by providing a curriculum. A curriculum was a weight-map, helping the StudentNet focus more on the samples with probably correct labels. After “teaching,” the curriculum decided by the MentorNet was updated by the feedback from the StudentNet. This iteration could avoid the performance drop caused by corrupted labels.
Briefly, like other exploration in DL fields, there are dissenting opinions of noise. Fortunately, the discussion of the function of noise activating novel and numerous methods to strengthen generalization performance. And for enlarging generalization, many aforementioned methods (dropout layers, data augmentation, and training/validation/test data split) are popularly and empirically used. However, a well-accepted theory has not yet been established.
E. Systematic Bias
For the ML community, there is no standard data processing pipeline. But for medical images, protocols could offer some insights to dodge hidden traps of bias. In datasheets for datasets presented by Gebru et al. [167], a list of questions can be asked to enhance reliability, including motivations, composition, collection process, preprocessing, uses, distribution, and maintenance. Who created the dataset, and for what purpose? Did the dataset include any errors, noise, or redundancies? Was there any sampling bias? In what protocol the dataset was acquired, and could the model be generalized to other protocol? Did volunteers consent to the collection and how to revoke their consent for future use? Was there any preprocessing that could introduce bias or noise? Were there any tasks inappropriate for the dataset? Were there any regulatory restrictions that should be obeyed? Extra effort to the dataset deliveries more ethical considerations and curtail more potential robustness risk.
F. Interpretability
Various methods are employed, based on empirical inspiration instead of theoretical proof, to expand and explore the interpretability of model performance. Most individuals will prefer a system with an understandable core with moderated loss in accuracy, rather than a complete “black box.” It is unrealistic to expect every parameter in a DL system to be explained, but a goal would be to consider a general answer for the question of “Why could we trust this result?” Or, in another way, “How should we interpret this result?”
1). Bayesian Network:
A Bayesian network is a probabilistic graph model representing magnitudes of dependencies between diverse variables. The network contains nodes and connections. The nodes are variables, and the connections are weights between two nodes, representing how much one node influences another. The advantage of a Bayesian network is that we can better understand the main factors of making a prediction.
In practice, a Bayesian network can be built to explain the weights of numerous features contributing to the final diagnosis. In Cook’s work [168], five categories are introduced.
Signal: The density of signals in the ROI of radiology modalities (T1- and T2-weighted MRI, CT, SPECT, and PET).
Spatial: The geographic features of abnormalities, such as locations, area, etc.
Time: The time-related features.
Clinical: Biological features of patients, such as gender, age, history of disease, etc.
Miscellaneous: The rest of the other valuable features.
In general, it is inefficient and meaningless to directly exploit the raw source. Different from a single DL model, radiologists and experts could inject their domain knowledge into a Bayesian network by proposing potential features and setting approximate weights for features as initials. There are plenty of ways to design and extract a feature, even training a CNN for automatically acquiring features from medical scans. Fig. 6 demonstrates the schema of the diagnostic system presented by Rauschecker et al. [169]. The U-Net structure is used to extract features for the candidates of diagnostic evidence. After quantitative features are extracted and calculated from segmented lesions, a Bayesian network is constructed for the final decision. For clinicians using such a DL system, they can both see the diagnosis and corresponding support, so they can interpret the result.
Fig. 6.
Overview of a Bayesian system. (a) Zoom-in view of the feature extraction network. (b) Unique networks are designed to extract specific features. (c) Quantitative features are calculated from the segmented. (d) Diagnosis is presented by the Bayesian network based on the set of features. *From A. M. Rauschecker et al., “AI System Approaching Neuroradiologist-Level Differential Diagnosis Accuracy at Brain MRI,” Radiology, vol. 295, no. 3, pp. 626–637, Apr. 2020, doi: 10.1148/radiol.2020190283.
A contemporary interpretation of CNNs is that the low-level layers focus on the details of images, such as lines, dots, corners, and the high-level layers makes decisions based on the results from low-level layers. In such a configuration, the Bayesian network at the end of the whole CNN provides a way to determine the weights of well-designed features. Comparing to the weights automatically learned by the network, a Bayesian network could provide clear insights of the decision procedure, at a moderated loss of accuracy.
2). Attention Map:
Another common approach is to study an attention map, which can be interpreted as a weight map of the whole image. For example, a human will determine the type of bird by observing its head, wings, and feet, while a CNN performs classification as a result of larger activations in certain regions of the image. We name this bias of influence across the whole image as attention. Jetly et al. presented a method of visualizing attention. It demonstrates the distribution of weights for different inputs, and help researchers know more inside the CNN.
A fully automated DL pipeline was presented by Lee et al. to perform bone age assessment [170]. In this research, the DL-based platform was trained to perform bone age assessment on radiographs of hands that were first segmented, standardized, and preprocessed by the pipeline. To increase the credibility of their system, representative attention maps were shown in Fig. 7 for four major skeletal maturity stages. For each skeletal maturity stage, the important areas of the image used by the trained model to perform the assessment are highlighted. The uncovered areas correspond to clinically relevant features used by clinicians when manually performing bone age assessment.
Fig. 7.
Selected examples of attention maps for female (upper rows) and male (lower rows) in the four major skeletal maturity stages: (a) prepuberty, (b) early-and-mid puberty, (c) late puberty, and (d) post-puberty stages. The yellow-red regions of the heatmaps indicate the portions of the images utilized by the DL-based pipeline to perform the bone age assessment. *From H. Lee et al., “Fully Automated DL System for Bone Age Assessment,” J Digit Imaging, vol. 30, no. 4, pp. 427–441, Aug. 2017, doi: 10.1007/s10278-017-9955-8. Lee et al. is an open-access article distributed under the terms of the Creative Commons CC BY license and no changes were made to this figure.
G. Transfer Learning and Domain Adaptation
Transfer learning is an efficient way to extend successfully trained networks to new data or tasks, especially when these networks can be trained with abundant or easy to label data. Transfer learning defines the general process of applying knowledge from one learned model to a similar problem, such as applying a different type of data, applying the model to a different task, or both. In the field of medical imaging, it is most common to adapt trained models to new types of data, for which this specific type of transfer learning is called domain adaptation. For example, domain adaptation would consist of transferring a model trained on one source domain (like T1-weighted MR images) and applying it to another target domain (like T2-weighted MR images), with the same tasks (like segmentation).
One widely accepted theory states that low-level layers focus on the extraction of basic elements in images, such as lines, corners, and circles and only high-level layers combine intermediate results in a task-dependent way, as seen in Fig. 3 [36]. Hence, the network trained on the source domain has the capacity of being transferred into the similar target domain, directly or with a few epochs of training. In the view that well-organized medical datasets and accompanying annotation are very time consuming, domain adaptation is potentially valuable due to its potential to reduce the requirement of large datasets and provide potential improvements in performance by better extraction of basic and generalizable features.
A favored method of domain adaptation is freezing a part of the pretrained network and fine-tuning (train with small a learning rate) the rest part. Chen et al. [171] transferred the model from the Montgomery set [172] to the JSRT set [173], performing unsupervised Chest X-ray segmentation. Dou et al. [174] studied on MRI-CT setting for segmentation. Gholami et al. [175] trained a model based on the synthetic brain tumorous dataset (generated from healthy brains) and tested in the real brain tumor dataset BraTS’18 [176]–[178]. Zhang et al. [179] extended the model from the labeled set (source) to the unlabeled set (target) in adenoma diagnosis. Mahmood et al. [180] trained the model learning from synthetic organ model images and tested in the monocular depth estimation for endoscopy images. Various applications of domain adaptations have been summarized above and more can be expected.
H. Upgradeable System
After the network has been trained and employed, it might be desirable to maintain and upgrade the network. This approach could reinforce the network by continuing training the network based on new, real-world training data. Hence, data faced in deployment are complementary to training. However, vulnerability may occur in extreme cases. Unseen and rare instances may cause instability of the whole system. Observation of the behavior of the system encountering uncommon inputs may provide interesting case studies to enable a deeper understanding of any required modifications. Additionally, feedback from users could also as a tool to enhance the robustness of the system. Experts could provide comments on the performance of the system to further improve accuracy and capability. Furthermore, models could be tuned to meet the specifications of individual users based on personalized preferences. In general, continuous observation on the operating performance of a DL system is a key to enabling steady robustness.
I. Adversarial Attacks
What if the system is maliciously attacked? In the work of Wernick et al. [181], the fast gradient sign method (FGSM) was introduced to construct perturbation for undermining the quality of results of the DL network. The main idea of this attack is to train the input image according to the gradient from the trained network. After this, iterative FGSM (i-FGSM) [182] and targeted i-FGSM (ti-FGSM) [182] were also created for a more effective attack. To defend attacks, two popular methods were proposed: 1) network distillation [183] and 2) adversarial samples augmentation [184]. The network distillation refers to the method of training a “student” network to learn the predictions from the original network. By controlling the parameter “Temperature” (T) during the distillation, the gradient of networks can be reduced; hence this can reduce the influence of perturbation or enhance the robustness. Adversarial samples augmentation, as the name suggests, is the approach to adding adversarial samples into the training dataset.
Liu et al. [185] presented an attack simulation with brain tumor segmentation. Fig. 8 shows how the incorrect segmentations under the adversarial perturbation reduce accuracy. Both methods could improve the accuracy under attack, but still worse than the model without attack. However, the medical imaging system is usually closed and off-contact for people without credentials. Additionally, the expertise of physicians and other healthcare workers may serve as a backup for adversarial DL systems, but it is critical to understand that DL systems are vulnerable to adversarial attacks, both unintentional (e.g., from image artifacts) and intentional (e.g., from bad actors).
Fig. 8.
Adversarial attacks on brain tumor segmentation of Liu et al. Three visually subtle adversarial attacks (FGSM, i-FGSM, and ti-FGSM) all influenced the segmentation results of brain tumors, compared to the reference (far left). Dice coefficient is greatly decreased due to the adversarial attacks. *From Z. Liu, J. Zhang, V. Jog, P.-L. Loh, and A. B. McMillan, “Robustifying Deep Networks for Image Segmentation,” arXiv:1908.00656 [cs, eess], Aug. 2019, Accessed: May 14, 2020. [Online]. Available: http://arxiv.org/abs/1908.00656.
Antun et al. [186] discussed the potential attacks from theoretical verification, great varieties, and basic remedy. The authors constructed three instability tests, including tiny worst-case perturbations, small structural changes, and the number of device samples changes, on six popular DL models. The results suggested that theoretically, the Lebesgue measure of the set of “bad” perturbation is greater than zero. So, there would be a nonzero probability that human-eye-detectable perturbations emerged. In the inspection of instability, artifacts were related to the network architecture and training set and were demonstrated ranging from nonexistence to blurring of details. Artifacts-specific retraining may mitigate target issues, but a general solution to artifacts, even a general prediction of emergency of artifacts was highly expected.
VI. Limitations
Although DL approaches have proven to be beneficial when addressing common problems within the medical imaging field, there are some limitations associated with its implementation. First, the ability of DL networks to achieve the desired performance is dependent on the quality and quantity of the available training data. DL approaches are suitable to perform complex calculations, but when there is not enough data available or the dataset is too homogeneous, models have a tendency to be overfitted. This characteristic of DL networks represents a challenge in the medical imaging field as the cost of collecting the data is usually high, obtaining ground-truth data is time consuming and requires expertise, and sharing data is not a straight forward process due to privacy concerns [187], [188]. For that reason, larger open-access medical image repositories, such as ADNI [131] and TCIA [132], are needed to continue improving the performance of these models. Another possible solution for this limitation is the possibility of sharing models between research institutions/industry to be further trained on new data, without jeopardizing the privacy, and thus improving generalizability through the concept of federated and distributed training procedures [189].
Another limitation of DL is its “black box” nature. Although DL networks can reach excellent performance, it is not always clear how or what the model is learning, although a great deal of new research is underway to meet these limitations. However, it can be challenging when applying DL models to the processing of medical images when a straightforward interpretation and justification of the performed analysis may be desired. Therefore, when solving problems for which the data are well structured, and there is a clear understanding of which are the optimal features, ML approaches may be more suitable because the models are capable of learning using preprogrammed criteria [190]. Moreover, ML approaches, such as SVM [191] and random forest [192], can be easier to implement and more effective in cases with smaller dataset sizes where an optimal representation of the data is available or can be obtained [190].
VII. Conclusion
There is no doubt that advances within the DL field have and will continue to positively impact the medical imaging field. Specifically, the ability of DL networks of learning high-level features from the data, without implementing a feature engineering step, make it a suitable alternative to ML methods when dealing with medical images. As a result, DL networks have been applied to solve a wide range of problems within the field, from disease detection to the synthesis of PET images from MRI scans and vice versa. Hence, this article presents a summary of the evolution of DL, describes the elements of the deep neural network, and attempts to define key steps necessary to implement a supervised DL application. Moreover, there is no doubt that DL is a valuable and exciting tool, but as with most methodologies, there are several limitations associated with its implementation that should be taken into consideration when applying these models. Furthermore, it is important to emphasize that DL models are not always preferred over ML ones and that the decision will be highly dependent on the problem at hand and the quality of the available data.
Acknowledgments
This work was supported by the National Institutes of Health under Award R01EB026708 and Award R01LM013151.
Contributor Information
Maribel Torres-Velázquez, Department of Biomedical Engineering, College of Engineering, University of Wisconsin–Madison, Madison, WI 53705 USA.
Wei-Jie Chen, Department of Electrical and Computer Engineering, College of Engineering, University of Wisconsin–Madison, Madison, WI 53705 USA.
Xue Li, Department of Radiology, University of Wisconsin School of Medicine and Public Health, University of Wisconsin–Madison, Madison, WI 53705 USA.
Alan B. McMillan, Department of Radiology, University of Wisconsin School of Medicine and Public Health, University of Wisconsin–Madison, Madison, WI 53705 USA, and also with the Department of Medical Physics, University of Wisconsin–Madison, Madison, WI 53705 USA.
References
- [1].Russell SJ, Artificial Intelligence: A Modern Approach, 2nd ed. Upper Saddle River, NJ, USA: Prentice-Hall, 2003. [Google Scholar]
- [2].Mitchell TM, Machine Learning. New York, NY, USA: McGraw-Hill, 1997. [Google Scholar]
- [3].Quinlan JR, “Induction of decision trees,” Mach Learn, vol. 1, no. 1, pp. 81–106, March. 1986, doi: 10.1007/BF00116251. [DOI] [Google Scholar]
- [4].Kaelbling LP, Littman ML, and Moore AW, “Reinforcement learning: A survey,” J. Artif. Int. Res, vol. 4, no. 1, pp. 237–285, May 1996. [Google Scholar]
- [5].Ben-Gal I, “Bayesian networks,” in Encyclopedia of Statistics in Quality and Reliability. Washington, DC, USA: Amer. Cancer Soc., 2008. [Google Scholar]
- [6].LeCun Y, Bengio Y, and Hinton G, “Deep learning,” Nature, vol. 521, no. 7553, pp. 436–444, May 2015, doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- [7].Schmidhuber J, “Deep learning in neural networks: An overview,” Neural Netw, vol. 61, pp. 85–117, January. 2015, doi: 10.1016/j.neunet.2014.09.003. [DOI] [PubMed] [Google Scholar]
- [8].Bengio Y, Courville A, and Vincent P, “Representation learning: A review and new perspectives,” IEEE Trans. Pattern Anal. Mach. Intell, vol. 35, no. 8, pp. 1798–1828, August. 2013, doi: 10.1109/TPAMI.2013.50. [DOI] [PubMed] [Google Scholar]
- [9].Advances in Independent Component Analysis and Learning Machines. London, U.K.: Elsevier, 2015. [Google Scholar]
- [10].Wu G, Lu W, Gao G, Zhao C, and Liu J, “Regional deep learning model for visual tracking,” Neurocomputing, vol. 175, pp. 310–323, January. 2016, doi: 10.1016/j.neucom.2015.10.064. [DOI] [Google Scholar]
- [11].Noda K, Yamaguchi Y, Nakadai K, Okuno HG, and Ogata T, “Audio-visual speech recognition using deep learning,” Appl. Intell, vol. 42, no. 4, pp. 722–737, June. 2015, doi: 10.1007/s10489-014-0629-7. [DOI] [Google Scholar]
- [12].Kohonen T, “An introduction to neural computing,” Neural Netw, vol. 1, no. 1, pp. 3–16, January. 1988, doi: 10.1016/0893-6080(88)90020-2. [DOI] [Google Scholar]
- [13].McCulloch WS and Pitts W, “A logical calculus of the ideas immanent in nervous activity,” Bull. Math. Biophys, vol. 5, no. 4, pp. 115–133, December. 1943, doi: 10.1007/BF02478259. [DOI] [PubMed] [Google Scholar]
- [14].Hebb DO, The Organization of Behavior: A Neuropsychological Theory. New York, NY, USA: Psychol., 2005. [Google Scholar]
- [15].Rosenblatt F, “The perceptron: A probabilistic model for information storage and organization in the brain,” Psychol. Rev, vol. 65, no. 6, pp. 386–408, 1958, doi: 10.1037/h0042519. [DOI] [PubMed] [Google Scholar]
- [16].Newell A, “Perceptrons. An introduction to computational geometry. Marvin minsky and seymour papert, MIT Press, Cambridge, Mass., 1969. vi + 258 pp., illus. Cloth, $12; paper, $4.95,” Science, vol. 165, no. 3895, pp. 780–782, August. 1969, doi: 10.1126/science.165.3895.780. [DOI] [Google Scholar]
- [17].Hubel DH and Wiesel TN, “Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex,” J. Physiol, vol. 160, no. 1, pp. 106–154, 1962, doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Hubel DH and Wiesel TN, “Receptive fields and functional architecture in two nonstriate visual areas (18 and 19) of the cat,” J. Neurophysiol, vol. 28, no. 2, pp. 229–289, March. 1965, doi: 10.1152/jn.1965.28.2.229. [DOI] [PubMed] [Google Scholar]
- [19].Hubel DH and Wiesel TN, “Ferrier lecture—Functional architecture of macaque monkey visual cortex,” Proc. Roy. Soc. London B Biol. Sci, vol. 198, no. 1130, pp. 1–59, May 1977, doi: 10.1098/rspb.1977.0085. [DOI] [PubMed] [Google Scholar]
- [20].Fukushima K, “Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position,” Biol. Cybern, vol. 36, no. 4, pp. 193–202, April. 1980, doi: 10.1007/BF00344251. [DOI] [PubMed] [Google Scholar]
- [21].Fukushima K, “Cognitron: A self-organizing multilayered neural network,” Biol. Cybern, vol. 20, no. 3, pp. 121–136, September. 1975, doi: 10.1007/BF00342633. [DOI] [PubMed] [Google Scholar]
- [22].Rumelhart DE, Hinton GE, and Williams RJ, “Learning representations by back-propagating errors,” Nature, vol. 323, no. 6088, pp. 533–536, October. 1986, doi: 10.1038/323533a0. [DOI] [Google Scholar]
- [23].LeCun Y et al. , “Backpropagation applied to handwritten zip code recognition,” Neural Comput, vol. 1, no. 4, pp. 541–551, December. 1989, doi: 10.1162/neco.1989.1.4.541. [DOI] [Google Scholar]
- [24].LeCun Y, Bottou L, Bengio Y, and Haffner P, “Gradient-based learning applied to document recognition,” Proc. IEEE, vol. 86, no. 11, pp. 2278–2324, November. 1998, doi: 10.1109/5.726791. [DOI] [Google Scholar]
- [25].Hinton GE, Osindero S, and Teh Y-W, “A fast learning algorithm for deep belief nets,” Neural Comput, vol. 18, no. 7, pp. 1527–1554, May 2006, doi: 10.1162/neco.2006.18.7.1527. [DOI] [PubMed] [Google Scholar]
- [26].Krizhevsky A, Sutskever I, and Hinton GE, “ImageNet classification with deep convolutional neural networks,” in Proc. Adv. Neural Inf. Process. Syst, 2012, pp. 1097–1105. [Google Scholar]
- [27].Simonyan K and Zisserman A, “Very deep convolutional networks for large-scale image recognition,” April. 2015. Accessed: Aug. 06, 2020. [Online]. Available: arXiv:1409.1556. [Google Scholar]
- [28].Szegedy C et al. (2015). Going Deeper With Convolutions. Accessed: Aug. 5, 2020. [Online]. Available: https://www.cv-foundation.org/openaccess/content_cvpr_2015/html/Szegedy_Going_Deeper_With_2015_CVPR_paper.html
- [29].Girshick R, Donahue J, Darrell T, and Malik J. (2014). Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. Accessed: Mar. 31, 2020. [Online]. Available: http://openaccess.thecvf.com/content_cvpr_2014/html/Girshick_Rich_Feature_Hierarchies_2014_CVPR_paper.html
- [30].Girshick R. (2015). Fast R-CNN. Accessed: Aug. 5, 2020. [Online]. Available: https://openaccess.thecvf.com/content_iccv_2015/html/Girshick_Fast_R-CNN_ICCV_2015_paper.html
- [31].Ren S, He K, Girshick R, and Sun J, “Faster R-CNN: Towards real-time object detection with region proposal networks,” in Proc. Adv. Neural Inf. Process. Syst, 2015, pp. 91–99. [DOI] [PubMed] [Google Scholar]
- [32].Long J, Shelhamer E, and Darrell T. (2015). Fully Convolutional Networks for Semantic Segmentation. Accessed: Aug. 5, 2020. [Online]. Available: https://www.cv-foundation.org/openaccess/content_cvpr_2015/html/Long_Fully_Convolutional_Networks_2015_CVPR_paper.html [DOI] [PubMed]
- [33].Ronneberger O, Fischer P, and Brox T, “U-Net: Convolutional networks for biomedical image segmentation,” in Proc. Med. Image Comput. Comput. Assist. Intervent. (MICCAI), 2015, pp. 234–241, doi: 10.1007/978-3-319-24574-4_28. [DOI] [Google Scholar]
- [34].He D et al. , “StNet: Local and global spatial–temporal modeling for action recognition,” in Proc. AAAI Conf. Artif. Intell, vol. 33, July. 2019, p. 1, doi: 10.1609/aaai.v33i01.33018401. [DOI] [Google Scholar]
- [35].Bergstra J and Bengio Y, “Random search for hyper-parameter optimization,” J. Mach. Learn. Res, vol. 13, pp. 281–305, February. 2012. [Google Scholar]
- [36].Meng F, Wang X, Shao F, Wang D, and Hua X, “Energy-efficient gabor kernels in neural networks with genetic algorithm training method,” Electronics, vol. 8, no. 1, p. 105, January. 2019, doi: 10.3390/electronics8010105. [DOI] [Google Scholar]
- [37].Goodfellow IJ, Bengio Y, and Courville A, Deep Learning. Cambridge, MA, USA: MIT Press, 2016. [Google Scholar]
- [38].Zhou Y-T and Chellappa R, “Computation of optical flow using a neural network,” in Proc. IEEE Int. Conf. Neural Netw, vol. 2, July. 1988, pp. 71–78, doi: 10.1109/ICNN.1988.23914. [DOI] [Google Scholar]
- [39].Chen H et al. , “Low-dose CT with a residual encoder–decoder convolutional neural network (RED-CNN),” IEEE Trans. Med. Imag, vol. 36, no. 12, pp. 2524–2535, December. 2017, doi: 10.1109/TMI.2017.2715284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Zeiler MD and Fergus R, “Visualizing and understanding convolutional networks,” in Proc. Comput. Vis. ECCV, 2014, pp. 818–833, doi: 10.1007/978-3-319-10590-1_53. [DOI] [Google Scholar]
- [41].Noh H, Hong S, and Han B. (2015). Learning Deconvolution Network for Semantic Segmentation. Accessed: Aug. 5, 2020. [Online]. Available: https://www.cv-foundation.org/openaccess/content_iccv_2015/html/Noh_Learning_Deconvolution_Network_ICCV_2015_paper.html
- [42].Yu F and Koltun V, “Multi-scale context aggregation by dilated convolutions,” in Proc. Conf. Track, San Juan, Puerto Rico, 2016, p. 13. [Google Scholar]
- [43].Hinton GE, “Rectified linear units improve restricted Boltzmann machines Vinod Nair,” in Proc. ICML, 2010, pp. 807–814. [Google Scholar]
- [44].Clevert D-A, Unterthiner T, and Hochreiter S, “Fast and accurate deep network learning by exponential linear units (ELUs),” presented at the 4th Int. Conf. Learn. Represent. (ICLR), San Juan, Puerto Rico, 2016. Accessed: Aug. 6, 2020. [Online]. Available: http://arxiv.org/abs/1511.07289 [Google Scholar]
- [45].He K, Zhang X, Ren S, and Sun J, “Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification,” in Proc. Conf. Track, 2015, pp. 1026–1034, doi: 10.1109/ICCV.2015.123. [DOI] [Google Scholar]
- [46].Ioffe S and Szegedy C, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Proc. Conf. Track, Lille, France, 2015, p. 9. [Google Scholar]
- [47].Srivastava N, Hinton G, Krizhevsky A, Sutskever I, and Salakhutdinov R, “DropOut: A simple way to prevent neural networks from overfitting,” J. Mach. Learn. Res, vol. 15, no. 1, pp. 1929–1958, January. 2014. [Google Scholar]
- [48].Zhu B, Liu JZ, Cauley SF, Rosen BR, and Rosen MS, “Image reconstruction by domain-transform manifold learning,” Nature, vol. 555, p. 7697, March. 2018, doi: 10.1038/nature25988. [DOI] [PubMed] [Google Scholar]
- [49].Du X, Cai Y, Wang S, and Zhang L, “Overview of deep learning,” in Proc. 31st Youth Acad. Annu. Conf. Chin. Assoc. Autom. (YAC), November. 2016, pp. 159–164, doi: 10.1109/YAC.2016.7804882. [DOI] [Google Scholar]
- [50].Nwankpa C, Ijomah W, Gachagan A, and Marshall S. (November. 2018). Activation Functions: Comparison of Trends in Practice and Research for Deep Learning. Accessed: May 5, 2020. [Online]. Available: http://arxiv.org/abs/1811.03378
- [51].Suk H-I and Shen D, “Deep learning-based feature representation for AD/MCI classification,” Med. Imag. Comput. Comput. Assist. Intervent, vol. 16, no. 2, pp. 583–590, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Suk H-I, Lee S-W, and Shen D, “Latent feature representation with stacked auto-encoder for AD/MCI diagnosis,” Brain Struct Funct, vol. 220, no. 2, pp. 841–859, March. 2015, doi: 10.1007/s00429-013-0687-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Suk H-I, Lee S-W, and Shen D, “Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis,” NeuroImage, vol. 101, pp. 569–582, November. 2014, doi: 10.1016/j.neuroimage.2014.06.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Shen T et al. , “Predicting Alzheimer disease from mild cognitive impairment with a deep belief network based on 18F-FDG-PET images,” Mol. Imag, vol. 18, pp. 1–9, September. 2019, doi: 10.1177/1536012119877285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Li F, Tran L, Thung K-H, Ji S, Shen D, and Li J, “A robust deep model for improved classification of AD/MCI patients,” IEEE J. Biomed. Health Informat, vol. 19, no. 5, pp. 1610–1616, September. 2015, doi: 10.1109/JBHI.2015.2429556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Suk H-I, Lee S-W, and Shen D, “Deep sparse multi-task learning for feature selection in Alzheimer’s disease diagnosis,” Brain Struct. Function, vol. 221, no. 5, pp. 2569–2587, 2016, doi: 10.1007/s00429-015-1059-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Lu D, Popuri K, Ding GW, Balachandar R, and Beg MF, “Multiscale deep neural network based analysis of FDG-PET images for the early diagnosis of Alzheimer’s disease,” Med. Image Anal, vol. 46, pp. 26–34, May 2018, doi: 10.1016/j.media.2018.02.002. [DOI] [PubMed] [Google Scholar]
- [58].Lu D, Popuri K, Ding GW, Balachandar R, and Beg MF, “Multimodal and multiscale deep neural networks for the early diagnosis of Alzheimer’s disease using structural MR and FDG-PET images,” Sci. Rep, vol. 8, no. 1, p. 5697, September. 2018, doi: 10.1038/s41598-018-22871-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Choi H and Jin KH, “Predicting cognitive decline with deep learning of brain metabolism and amyloid imaging,” Behav. Brain Res, vol. 344, pp. 103–109, May 2018, doi: 10.1016/j.bbr.2018.02.017. [DOI] [PubMed] [Google Scholar]
- [60].Liu M, Cheng D, Wang K, and Wang Y, “Multi-modality cascaded convolutional neural networks for Alzheimer’s disease diagnosis,” Neuroinformatics, vol. 16, nos. 3–4, pp. 295–308, October. 2018, doi: 10.1007/s12021-018-9370-4. [DOI] [PubMed] [Google Scholar]
- [61].Liu M, Cheng D, and Yan W, “Classification of Alzheimer’s disease by combination of convolutional and recurrent neural networks using FDG-PET images,” Front. Neuroinf, vol. 12, p. 35, June. 2018, doi: 10.3389/fninf.2018.00035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Son HJ et al. , “The clinical feasibility of deep learning-based classification of amyloid PET images in visually equivocal cases,” Eur. J. Nucl. Med. Mol. Imag, vol. 47, no. 2, pp. 332–341, February. 2020, doi: 10.1007/s00259-019-04595-y. [DOI] [PubMed] [Google Scholar]
- [63].Punjabi A, Martersteck A, Wang Y, Parrish TB, and Katsaggelos AK, “Neuroimaging modality fusion in Alzheimer’s classification using convolutional neural networks,” PLoS ONE, vol. 14, no. 12, December. 2019, Art. no. e0225759, doi: 10.1371/journal.pone.0225759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Huang Y, Xu J, Zhou Y, Tong T, and Zhuang X, “Diagnosis of Alzheimer’s disease via multi-modality 3D convolutional neural network,” Front Neurosci, vol. 13, p. 509, May 2019, doi: 10.3389/fnins.2019.00509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Choi H, Ha S, Im HJ, Paek SH, and Lee DS, “Refining diagnosis of Parkinson’s disease with deep learning-based interpretation of dopamine transporter imaging,” Neuroimage Clin, vol. 16, pp. 586–594, September. 2017, doi: 10.1016/j.nicl.2017.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Shen T et al. , “Use of overlapping group LASSO sparse deep belief network to discriminate Parkinson’s disease and normal control,” Front. Neurosci, vol. 13, p. 396, April. 2019, doi: 10.3389/fnins.2019.00396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Nobashi T et al. , “Performance comparison of individual and ensemble CNN models for the classification of brain 18F-FDG-PET scans,” J. Digit. Imag, vol. 33, pp. 447–455, October. 2020, doi: 10.1007/s10278-019-00289-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Betancur J et al. , “Deep learning analysis of upright-supine high-efficiency SPECT myocardial perfusion imaging for prediction of obstructive coronary artery disease: A multicenter study,” J. Nucl. Med, vol. 60, no. 5, pp. 664–670, May 2019, doi: 10.2967/jnumed.118.213538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Szegedy C, Vanhoucke V, Ioffe S, Shlens J, and Wojna Z. (2016). Rethinking the Inception Architecture for Computer Vision. Accessed: Aug. 5, 2020. [Online]. Available: https://www.cv-foundation.org/openaccess/content_cvpr_2016/html/Szegedy_Rethinking_the_Inception_CVPR_2016_paper.html
- [70].Togo R et al. , “Cardiac sarcoidosis classification with deep convolutional neural network-based features using polar maps,” Comput. Biol. Med, vol. 104, pp. 81–86, January. 2019, doi: 10.1016/j.compbiomed.2018.11.008. [DOI] [PubMed] [Google Scholar]
- [71].Ypsilantis P-P et al. , “Predicting response to neoadjuvant chemotherapy with PET imaging using convolutional neural networks,” PLoS ONE, vol. 10, no. 9, September. 2015, Art. no. e0137036, doi: 10.1371/journal.pone.0137036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Amyar A, Ruan S, Gardin I, Chatelain C, Decazes P, and Modzelewski R, “3-D RPET-NET: Development of a 3-D PET imaging convolutional neural network for radiomics analysis and outcome prediction,” IEEE Trans. Radiat. Plasma Med. Sci, vol. 3, no. 2, pp. 225–231, March. 2019, doi: 10.1109/TRPMS.2019.2896399. [DOI] [Google Scholar]
- [73].Shen W-C et al. , “Prediction of local relapse and distant metastasis in patients with definitive chemoradiotherapy-treated cervical cancer by deep learning from [18F]-fluorodeoxyglucose positron emission tomography/computed tomography,” Eur. Radiol, vol. 29, no. 12, pp. 6741–6749, December. 2019, doi: 10.1007/s00330-019-06265-x. [DOI] [PubMed] [Google Scholar]
- [74].Luo Y et al. , “Development of a fully cross-validated Bayesian network approach for local control prediction in lung cancer,” IEEE Trans. Radiat. Plasma Med. Sci, vol. 3, no. 2, pp. 232–241, March. 2019, doi: 10.1109/TRPMS.2018.2832609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Hatt M, Parmar C, Qi J, and Naqa IE, “Machine (deep) learning methods for image processing and radiomics,” IEEE Trans. Radiat. Plasma Med. Sci, vol. 3, no. 2, pp. 104–108, March. 2019, doi: 10.1109/TRPMS.2019.2899538. [DOI] [Google Scholar]
- [76].Wang H et al. , “Comparison of machine learning methods for classifying mediastinal lymph node metastasis of non-small cell lung cancer from 18F-FDG PET/CT images,” EJNMMI Res, vol. 7, p. 11, March. 2017, doi: 10.1186/s13550-017-0260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Kirienko M et al. , “Convolutional neural networks promising in lung cancer T-parameter assessment on baseline FDG-PET/CT,” Contrast Media Mol. Imag, vol. 2018, October. 2018, Art. no. 1382309, doi: 10.1155/2018/1382309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Perk T et al. , “Automated classification of benign and malignant lesions in 18F-NaF PET/CT images using machine learning,” Phys. Med. Biol, vol. 63, no. 22, November. 2018, Art. no. 225019, doi: 10.1088/1361-6560/aaebd0. [DOI] [PubMed] [Google Scholar]
- [79].Matsui Y et al. , “Prediction of lower-grade glioma molecular subtypes using deep learning,” J. Neurooncol, vol. 146, no. 2, pp. 321–327, January. 2020, doi: 10.1007/s11060-019-03376-9. [DOI] [PubMed] [Google Scholar]
- [80].Ithapu VK, Singh V, Okonkwo OC, Chappell RJ, Dowling NM, and Johnson SC, “Imaging based enrichment criteria using deep learning algorithms for efficient clinical trials in MCI,” Alzheimers Dement, vol. 11, no. 12, pp. 1489–1499, December. 2015, doi: 10.1016/j.jalz.2015.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Cole JH et al. , “Predicting brain age with deep learning from raw imaging data results in a reliable and heritable biomarker,” NeuroImage, vol. 163, pp. 115–124, December. 2017, doi: 10.1016/j.neuroimage.2017.07.059. [DOI] [PubMed] [Google Scholar]
- [82].Choi H, Ha S, Kang H, Lee H, and Lee DS, “Deep learning only by normal brain PET identify unheralded brain anomalies,” EBioMedicine, vol. 43, pp. 447–453, April. 2019, doi: 10.1016/j.ebiom.2019.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [83].Shaish H, Mutasa S, Makkar J, Chang P, Schwartz L, and Ahmed F, “Prediction of lymph node maximum standardized uptake value in patients with cancer using a 3D convolutional neural network: A proof-of-concept study,” Amer. J. Roentgenol, vol. 212, no. 2, pp. 238–244, 2019, doi: 10.2214/AJR.18.20094. [DOI] [PubMed] [Google Scholar]
- [84].Li H et al. , “Deep convolutional neural networks for imaging data based survival analysis of rectal cancer,” in Proc. IEEE 16th Int. Symp. Biomed. Imag. (ISBI), April. 2019, pp. 846–849, doi: 10.1109/ISBI.2019.8759301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Berg E and Cherry SR, “Using convolutional neural networks to estimate time-of-flight from PET detector waveforms,” Phys. Med. Biol, vol. 63, no. 2, November. 2018, Art. no. 02LT01, doi: 10.1088/1361-6560/aa9dc5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86].Hu P, Wu F, Peng J, Liang P, and Kong D, “Automatic 3D liver segmentation based on deep learning and globally optimized surface evolution,” Phys. Med. Biol, vol. 61, no. 24, pp. 8676–8698, December. 2016, doi: 10.1088/1361-6560/61/24/8676. [DOI] [PubMed] [Google Scholar]
- [87].Oh KT, Lee S, Lee H, Yun M, and Yoo SK, “Semantic segmentation of white matter in FDG-PET using generative adversarial network,” J. Digit. Imag, vol. 33, pp. 816–825, February. 2020, doi: 10.1007/s10278-020-00321-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [88].Blanc-Durand P, Van Der Gucht A, Schaefer N, Itti E, and Prior JO, “Automatic lesion detection and segmentation of 18F-FET PET in gliomas: A full 3D U-Net convolutional neural network study,” PLoS ONE, vol. 13, p. 4, April. 2018, doi: 10.1371/journal.pone.0195798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [89].Huang B et al. , “Fully automated delineation of gross tumor volume for head and neck cancer on PET-CT using deep learning: A dual-center study,” Contrast Media Mol. Imag, vol. 2018, Art. no. 8923028, October. 2018, doi: 10.1155/2018/8923028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90].Guo Z, Guo N, Gong K, Zhong S, and Li Q, “Gross tumor volume segmentation for head and neck cancer radiotherapy using deep dense multi-modality network,” Phys. Med. Biol, vol. 64, no. 20, October. 2019, Art. no. 205015, doi: 10.1088/1361-6560/ab440d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91].Zhao L, Lu Z, Jiang J, Zhou Y, Wu Y, and Feng Q, “Automatic nasopharyngeal carcinoma segmentation using fully convolutional networks with auxiliary paths on dual-modality PET-CT images,” J. Digit. Imag, vol. 32, no. 3, pp. 462–470, June. 2019, doi: 10.1007/s10278-018-00173-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92].Zhao X, Li L, Lu W, and Tan S, “Tumor co-segmentation in PET/CT using multi-modality fully convolutional neural network,” Phys. Med. Biol, vol. 64, no. 1, December. 2018, Art. no. 015011, doi: 10.1088/1361-6560/aaf44b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [93].Zhong Z et al. , “3D fully convolutional networks for co-segmentation of tumors on PET-CT images,” in Proc. IEEE Int. Symp. Biomed. Imag, vol. 2018, pp. 228–231, April. 2018, doi: 10.1109/ISBI.2018.8363561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [94].Zhong Z et al. , “Simultaneous cosegmentation of tumors in PET-CT images using deep fully convolutional networks,” Med. Phys, vol. 46, no. 2, pp. 619–633, February. 2019, doi: 10.1002/mp.13331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [95].Hu X et al. , “Coarse-to-fine adversarial networks and zone-based uncertainty analysis for NK/T-cell lymphoma segmentation in CT/PET images,” IEEE J. Biomed. Health Inform, vol. 24, no. 9, pp. 2599–2608, September. 2020, doi: 10.1109/JBHI.2020.2972694. [DOI] [PubMed] [Google Scholar]
- [96].Xia X and Kulis B. (November. 2017). W-Net: A Deep Model for Fully Unsupervised Image Segmentation. Accessed: May 5, 2020. [Online]. Available: http://arxiv.org/abs/1711.08506.
- [97].Xu L et al. , “Automated whole-body bone lesion detection for multiple myeloma on 68Ga-pentixafor PET/CT imaging using deep learning methods,” Contrast Media Mol. Imag, vol. 2018, January. 2018, Art. no. 2391925, doi: 10.1155/2018/2391925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [98].Guo Z, Li X, Huang H, Guo N, and Li Q, “Deep learning-based image segmentation on multimodal medical imaging,” IEEE Trans. Radiat. Plasma Med. Sci, vol. 3, no. 2, pp. 162–169, March. 2019, doi: 10.1109/TRPMS.2018.2890359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [99].Hwang D et al. , “Improving the accuracy of simultaneously reconstructed activity and attenuation maps using deep learning,” J. Nucl. Med, vol. 59, no. 10, pp. 1624–1629, 2018, doi: 10.2967/jnumed.117.202317. [DOI] [PubMed] [Google Scholar]
- [100].Hwang D et al. , “Generation of PET attenuation map for whole-body time-of-flight 18F-FDG PET/MRI using a deep neural network trained with simultaneously reconstructed activity and attenuation maps,” J. Nucl. Med, vol. 60, no. 8, pp. 1183–1189, 2019, doi: 10.2967/jnumed.118.219493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101].Liu F, Jang H, Kijowski R, Bradshaw T, and McMillan AB, “Deep learning MR imaging-based attenuation correction for PET/MR imaging,” Radiology, vol. 286, no. 2, pp. 676–684, February. 2018, doi: 10.1148/radiol.2017170700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [102].Liu F, Jang H, Kijowski R, Zhao G, Bradshaw T, and McMillan AB, “A deep learning approach for 18F-FDG PET attenuation correction,” EJNMMI Phys, vol. 5, no. 1, p. 24, December. 2018, doi: 10.1186/s40658-018-0225-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [103].Arabi H, Zeng G, Zheng G, and Zaidi H, “Novel adversarial semantic structure deep learning for MRI-guided attenuation correction in brain PET/MRI,” Eur. J. Nucl. Med. Mol. Imag, vol. 46, no. 13, pp. 2746–2759, December. 2019, doi: 10.1007/s00259-019-04380-x. [DOI] [PubMed] [Google Scholar]
- [104].Ladefoged CN et al. , “A multi-centre evaluation of eleven clinically feasible brain PET/MRI attenuation correction techniques using a large cohort of patients,” Neuroimage, vol. 147, pp. 346–359, February. 2017, doi: 10.1016/j.neuroimage.2016.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [105].Ladefoged CN, Marner L, Hindsholm A, Law I, Højgaard L, and Andersen FL, “Deep learning based attenuation correction of PET/MRI in pediatric brain tumor patients: Evaluation in a clinical setting,” Front Neurosci, vol. 12, p. 1005, January. 2019, doi: 10.3389/fnins.2018.01005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [106].Torrado-Carvajal A et al. , “Dixon-VIBE deep learning (DIVIDE) pseudo-CT synthesis for pelvis PET/MR attenuation correction,” J. Nucl. Med, vol. 60, no. 3, pp. 429–435, 2019, doi: 10.2967/jnumed.118.209288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [107].Gong K et al. , “MR-based attenuation correction for brain PET using 3D cycle-consistent adversarial network,” IEEE Trans. Radiat. Plasma Med. Sci, early access, Jul. 3, 2020, doi: 10.1109/TRPMS.2020.3006844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [108].Lee JS, “A review of deep learning-based approaches for attenuation correction in positron emission tomography,” IEEE Trans. Radiat. Plasma Med. Sci, early access, Jul. 17, 2020, doi: 10.1109/TRPMS.2020.3009269. [DOI] [Google Scholar]
- [109].Häggström I, Schmidtlein CR, Campanella G, and Fuchs TJ, “DeepPET: A deep encoder–decoder network for directly solving the PET image reconstruction inverse problem,” Med. Image Anal, vol. 54, pp. 253–262, May 2019, doi: 10.1016/j.media.2019.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [110].Cui J, Liu X, Wang Y, and Liu H, “Deep reconstruction model for dynamic PET images,” PLoS ONE, vol. 12, no. 9, 2017, Art. no. e0184667, doi: 10.1371/journal.pone.0184667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [111].Spuhler KD, Gardus J, Gao Y, DeLorenzo C, Parsey R, and Huang C, “Synthesis of patient-specific transmission data for PET attenuation correction for PET/MRI neuroimaging using a convolutional neural network,” J. Nucl. Med, vol. 60, no. 4, pp. 555–560, 2019, doi: 10.2967/jnumed.118.214320. [DOI] [PubMed] [Google Scholar]
- [112].Li R et al. , “Deep learning based imaging data completion for improved brain disease diagnosis,” Med. Imag. Comput. Assist. Intervent, vol. 17, no. 3, pp. 305–312, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [113].Choi H and Lee DS, “Generation of structural MR images from amyloid PET: Application to MR-less quantification,” J. Nucl. Med, vol. 59, no. 7, pp. 1111–1117, 2018, doi: 10.2967/jnumed.117.199414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [114].Guo J, Gong E, Fan AP, Goubran M, Khalighi MM, and Zaharchuk G, “Predicting 15O-water PET cerebral blood flow maps from multi-contrast MRI using a deep convolutional neural network with evaluation of training cohort bias,” J. Cerebr. Blood Flow Metab, vol. 40, no. 11, pp. 2240–2253, November. 2019, doi: 10.1177/0271678X19888123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [115].Wei W et al. , “Learning myelin content in multiple sclerosis from multimodal MRI through adversarial training,” in Proc. Med. Image Comput. Comput. Assist. Intervent. (MICCAI), 2018, pp. 514–522, doi: 10.1007/978-3-030-00931-1_59. [DOI] [Google Scholar]
- [116].Reader AJ, Corda G, Mehranian A, da Costa-Luis C, Ellis S, and Schnabel JA, “Deep learning for PET image reconstruction,” IEEE Trans. Radiat. Plasma Med. Sci, early access, Aug. 6, 2020, doi: 10.1109/TRPMS.2020.3014786. [DOI] [Google Scholar]
- [117].Shao W, Pomper MG, and Du Y, “A learned reconstruction network for SPECT imaging,” IEEE Trans. Radiat. Plasma Med. Sci, early access, May 12, 2020, doi: 10.1109/TRPMS.2020.2994041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [118].Shan H et al. , “3D convolutional encoder–decoder network for low-dose CT via transfer learning from a 2D trained network,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1522–1534, June. 2018, doi: 10.1109/TMI.2018.2832217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [119].Yang Q et al. , “Low dose CT image denoising using a generative adversarial network with wasserstein distance and perceptual loss,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1348–1357, June. 2018, doi: 10.1109/TMI.2018.2827462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [120].You C et al. , “Structurally-sensitive multi-scale deep neural network for low-dose CT denoising,” IEEE Access, vol. 6, pp. 41839–41855, 2018, doi: 10.1109/ACCESS.2018.2858196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Hasan AM, Mohebbian MR, Wahid KA, and Babyn P, “Hybrid collaborative Noise2Noise denoiser for low-dose CT images,” IEEE Trans. Radiat. Plasma Med. Sci, early access, May 12, 2020, doi: 10.1109/TRPMS.2020.3002178. [DOI] [Google Scholar]
- [122].Zhang F et al. , “REDAEP: Robust and enhanced denoising autoencoding prior for sparse-view CT reconstruction,” IEEE Trans. Radiat. Plasma Med. Sci, early access, Apr. 22, 2020, doi: 10.1109/TRPMS.2020.2989634. [DOI] [Google Scholar]
- [123].Kadimesetty VS, Gutta S, Ganapathy S, and Yalavarthy PK, “Convolutional neural network-based robust denoising of low-dose computed tomography perfusion maps,” IEEE Trans. Radiat. Plasma Med. Sci, vol. 3, no. 2, pp. 137–152, March. 2019, doi: 10.1109/TRPMS.2018.2860788. [DOI] [Google Scholar]
- [124].Xiang L, Qiao Y, Nie D, An L, Wang Q, and Shen D, “Deep auto-context convolutional neural networks for standard-dose PET image estimation from low-dose PET/MRI,” Neurocomputing, vol. 267, pp. 406–416, December. 2017, doi: 10.1016/j.neucom.2017.06.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [125].Wang Y et al. , “Locality adaptive multi-modality GANs for high-quality PET image synthesis,” Med. Imag. Comput. Assist. Intervent, vol. 11070, pp. 329–337, September. 2018, doi: 10.1007/978-3-030-00928-1_38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [126].Wang Y et al. , “3D auto-context-based locality adaptive multi-modality GANs for PET synthesis,” IEEE Trans. Med. Imag, vol. 38, no. 6, pp. 1328–1339, June. 2019, doi: 10.1109/TMI.2018.2884053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [127].Chen KT et al. , “Ultra–low-dose 18F-florbetaben amyloid PET imaging using deep learning with multi-contrast MRI inputs,” Radiology, vol. 290, no. 3, pp. 649–656, March. 2019, doi: 10.1148/radiol.2018180940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [128].Gong K, Guan J, Liu C-C, and Qi J, “PET image denoising using a deep neural network through fine tuning,” IEEE Trans. Radiat. Plasma Med. Sci, vol. 3, no. 2, pp. 153–161, March. 2019, doi: 10.1109/TRPMS.2018.2877644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [129].Li Y, Sixou B, Burghard A, and Peyrin F, “Investigation of semi-coupled dictionary learning in 3-D super resolution HR-pQCT imaging,” IEEE Trans. Radiat. Plasma Med. Sci, vol. 3, no. 2, pp. 129–136, March. 2019, doi: 10.1109/TRPMS.2018.2881488. [DOI] [Google Scholar]
- [130].Song T-A, Chowdhury SR, Yang F, and Dutta J, “PET image super-resolution using generative adversarial networks,” Neural Netw, vol. 125, pp. 83–91, May 2020, doi: 10.1016/j.neunet.2020.01.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [131].Petersen RC et al. , “Alzheimer’s disease neuroimaging initiative (ADNI): Clinical characterization,” Neurology, vol. 74, no. 3, pp. 201–209, January. 2010, doi: 10.1212/WNL.0b013e3181cb3e25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [132].Clark K et al. , “The cancer imaging archive (TCIA): Maintaining and operating a public information repository,” J. Digit. Imag, vol. 26, no. 6, pp. 1045–1057, December. 2013, doi: 10.1007/s10278-013-9622-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [133].O’Shea K and Nash R. (December. 2015). An Introduction to Convolutional Neural Networks. Accessed: May 7, 2020. [Online]. Available: http://arxiv.org/abs/1511.08458.
- [134].He K, Zhang X, Ren S, and Sun J, “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), June. 2016, pp. 770–778, doi: 10.1109/CVPR.2016.90. [DOI] [Google Scholar]
- [135].Huang G, Liu Z, Van Der Maaten L, and Weinberger KQ, “Densely connected convolutional networks,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), July. 2017, pp. 2261–2269, doi: 10.1109/CVPR.2017.243. [DOI] [Google Scholar]
- [136].Rumelhart DE, Hinton GE, and Williams RJ, “Learning internal representations by error propagation,” in Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1: Foundations. Cambridge, MA, USA: MIT Press, 1986, pp. 318–362. [Google Scholar]
- [137].Vincent P, Larochelle H, Lajoie I, Bengio Y, and Manzagol P-A, “Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion,” J. Mach. Learn. Res, vol. 11, no. 1, pp. 3371–3408, 2010, doi: 10.1002/qre.2392. [DOI] [Google Scholar]
- [138].Kingma DP and Welling M, “An introduction to variational autoencoders,” FNT Mach. Learn, vol. 12, no. 4, pp. 307–392, 2019, doi: 10.1561/2200000056. [DOI] [Google Scholar]
- [139].Goodfellow IJ et al. , “Generative adversarial nets,” in Proc. Conf. Track, Cambridge, MA, USA, vol. 2, 2014, pp. 2672–2680. [Google Scholar]
- [140].Smolensky P, “Information processing in dynamical systems: Foundations of harmony theory,” in Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1: Foundations. Cambridge, MA, USA: MIT Press, 1986, pp. 194–281. [Google Scholar]
- [141].Hinton GE, “Reducing the dimensionality of data with neural networks,” Science, vol. 313, no. 5786, pp. 504–507, July. 2006, doi: 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
- [142].Salakhutdinov R and Hinton G, “Deep Boltzmann machines,” Artif. Intell. Stat, vol. 5, pp. 448–455, April. 2009. [Google Scholar]
- [143].Ripley BD, Pattern Recognition and Neural Networks. Cambridge, U.K.: Cambridge Univ. Press, 2007. [Google Scholar]
- [144].James G, Witten D, Hastie T, and Tibshirani R, An Introduction to Statistical Learning, vol. 103. New York, NY, USA: Springer, 2013. [Google Scholar]
- [145].Kohavi R, “A study of cross-validation and bootstrap for accuracy estimation and model selection,” in Proc. Conf. Track, vol. 2. San Francisco, CA, USA, 1995, pp. 1137–1143. [Google Scholar]
- [146].Huber PJ, “Robust estimation of a location parameter,” Ann. Math. Stat, vol. 35, no. 1, pp. 73–101, 1964. [Google Scholar]
- [147].Johnson J, Alahi A, and Fei-Fei L, “Perceptual losses for real-time style transfer and super-resolution,” in Proc. Comput. Vis. ECCV, 2016, pp. 694–711, doi: 10.1007/978-3-319-46475-6_43. [DOI] [Google Scholar]
- [148].Qian N, “On the momentum term in gradient descent learning algorithms,” Neural Netw, vol. 12, no. 1, pp. 145–151, January. 1999, doi: 10.1016/S0893-6080(98)00116-6. [DOI] [PubMed] [Google Scholar]
- [149].Nesterov Y, “A method for unconstrained convex minimization problem with the rate of convergence O(1/k2),” Doklady USSR, vol. 269, no. 3, pp. 543–547, 1983. [Google Scholar]
- [150].Duchi J, Hazan E, and Singer Y, “Adaptive subgradient methods for online learning and stochastic optimization,” J. Mach. Learn. Res, vol. 12, no. 61, pp. 2121–2159, 2011. [Google Scholar]
- [151].Zeiler MD. (December. 2012). ADADELTA: An Adaptive Learning Rate Method. Accessed: Apr. 29, 2020. [Online]. Available: http://arxiv.org/abs/1212.5701.
- [152].Kingma DP and Ba J, “Adam: A method for stochastic optimization,” presented at the 3rd Int. Conf. Learn. Represent. (ICLR), San Diego, CA, USA, 2015. Accessed: Aug. 6, 2020. [Online]. Available: http://arxiv.org/abs/1412.6980. [Google Scholar]
- [153].Food and Drug Administration. (April. 2019). Proposed Regulatory Framework for Modifications to Artificial Intelligence/Machine Learning (AI/ML)-Based Software as a Medical Device (SaMD). [Online]. Available: https://www.fda.gov/media/122535/download.
- [154].U.K. Department of Health and Social Care. Code of Conduct for Data-Driven Health and Care Technology. Accessed: Mar. 23, 2020. [Online]. Available: https://www.gov.uk/government/publications/code-of-conduct-for-data-driven-health-and-care-technology/initial-code-of-conduct-for-data-driven-health-and-care-technology
- [155].Valiant LG, “A theory of the learnable,” Commun. ACM, vol. 27, no. 11, pp. 1134–1142, 1984, doi: 10.1145/1968.1972. [DOI] [Google Scholar]
- [156].Shorten C and Khoshgoftaar TM, “A survey on image data augmentation for deep learning,” J. Big Data, vol. 6, no. 1, p. 60, December. 2019, doi: 10.1186/s40537-019-0197-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [157].Hussain Z, Gimenez F, Yi D, and Rubin D, “Differential data augmentation techniques for medical imaging classification tasks,” AMIA Annu. Symp. Process, vol. 2017, pp. 979–984, April. 2018. [PMC free article] [PubMed] [Google Scholar]
- [158].Hansen LK and Salamon P, “Neural network ensembles,” IEEE Trans. Pattern Anal. Mach. Intell, vol. 12, no. 10, pp. 993–1001, October. 1990, doi: 10.1109/34.58871. [DOI] [Google Scholar]
- [159].Ho TK, Hull JJ, and Srihari SN, “Decision combination in multiple classifier systems,” IEEE Trans. Pattern Anal. Mach. Intell, vol. 16, no. 1, pp. 66–75, January. 1994, doi: 10.1109/34.273716. [DOI] [Google Scholar]
- [160].Woods K, Kegelmeyer WP, and Bowyer K, “Combination of multiple classifiers using local accuracy estimates,” IEEE Trans. Pattern Anal. Mach. Intell, vol. 19, no. 4, pp. 405–410, April. 1997, doi: 10.1109/34.588027. [DOI] [Google Scholar]
- [161].Giacinto G and Roli F, “Adaptive selection of image classifiers,” in Image Analysis and Processing. Berlin, Germany: Springer, 1997, pp. 38–45, doi: 10.1007/3-540-63507-6_182. [DOI] [Google Scholar]
- [162].Isensee F et al. (September. 2018). nnU-Net: Self-Adapting Framework for U-Net-Based Medical Image Segmentation. Accessed: Sep. 18, 2020. [Online]. Available: http://arxiv.org/abs/1809.10486
- [163].Kawaguchi K, Kaelbling LP, and Bengio Y. (July. 2020). Generalization in Deep Learning. Accessed: Jul. 29, 2020. [Online]. Available: http://arxiv.org/abs/1710.05468
- [164].Zhang C, Bengio S, and Hardt M, “Understanding deep learning requires re-thinking generalization,” in Proc. Conf. Track, Toulon, France, 2017, p. 15. [Google Scholar]
- [165].Goldberger J and Ben-Reuven E. (November. 2016). Training Deep Neural-Networks Using a Noise Adaptation Layer. Accessed: Aug. 6, 2020. [Online]. Available: https://openreview.net/forum?id=H12GRgcxg¬eId=H12GRgcxg.
- [166].Jiang L, Zhou Z, Leung T, Li L-J, and Fei-Fei L, “MentorNet: Learning data-driven curriculum for very deep neural networks on corrupted labels,” in Proc. Int. Conf. Mach. Learn, July. 2018, pp. 2304–2313. Accessed: Aug. 6, 2020. [Online]. Available: http://proceedings.mlr.press/v80/jiang18c.html [Google Scholar]
- [167].Gebru T et al. , “Datasheets for datasets,” March. 2020, Accessed: Mar. 23, 2020. [Online]. Available: http://arxiv.org/abs/1803.09010.
- [168].Cook T et al. , “Bayesian network interface for assisting radiology interpretation and education,” in Proc. Med. Imag. Informat. Healthcare Res. Appl, March. 2018, p. 26, doi: 10.1117/12.2293691. [DOI] [Google Scholar]
- [169].Rauschecker AM et al. , “Artificial intelligence system approaching neuroradiologist-level differential diagnosis accuracy at brain MRI,” Radiology, vol. 295, no. 3, pp. 626–637, April. 2020, doi: 10.1148/radiol.2020190283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [170].Lee H et al. , “Fully automated deep learning system for bone age assessment,” J. Digit. Imag, vol. 30, no. 4, pp. 427–441, August. 2017, doi: 10.1007/s10278-017-9955-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [171].Chen C, Dou Q, Chen H, and Heng P-A, “Semantic-aware generative adversarial nets for unsupervised domain adaptation in chest X-ray segmentation,” in Machine Learning in Medical Imaging. Cham, Switzerland: Springer, 2018, pp. 143–151, doi: 10.1007/978-3-030-00919-9_17. [DOI] [Google Scholar]
- [172].Jaeger S, Candemir S, Antani S, Wáng Y-XJ, Lu P-X, and Thoma G, “Two public chest X-ray datasets for computer-aided screening of pulmonary diseases,” Quant. Imag. Med. Surg, vol. 4, no. 6, pp. 475–477, December. 2014, doi: 10.3978/j.issn.2223-4292.2014.11.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [173].Shiraishi J et al. , “Development of a digital image database for chest radiographs with and without a lung nodule: Receiver operating characteristic analysis of radiologists’ detection of pulmonary nodules,” Amer. J. Roentgenol, vol. 174, no. 1, pp. 71–74, January. 2000, doi: 10.2214/ajr.174.1.1740071. [DOI] [PubMed] [Google Scholar]
- [174].Dou Q, Ouyang C, Chen C, Chen H, and Heng P-A, “Unsupervised cross-modality domain adaptation of ConvNets for biomedical image segmentations with adversarial loss,” in Proc. Conf. Track, Stockholm, Sweden, 2018, pp. 691–697, doi: 10.24963/ijcai.2018/96. [DOI] [Google Scholar]
- [175].Gholami A et al. , “A novel domain adaptation framework for medical image segmentation,” in Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries. Cham, Switzerland: Springer, 2019, pp. 289–298, doi: 10.1007/978-3-030-11726-9_26. [DOI] [Google Scholar]
- [176].Bakas S et al. , “Advancing the cancer genome atlas glioma MRI collections with expert segmentation labels and radiomic features,” Sci. Data, vol. 4, May 2017, Art. no. 170117, doi: 10.1038/sdata.2017.117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [177].Bakas S et al. (April. 2019). Identifying the Best Machine Learning Algorithms for Brain Tumor Segmentation, Progression Assessment, and Overall Survival Prediction in the BRATS Challenge. Accessed: Jul. 30, 2020. [Online]. Available: http://arxiv.org/abs/1811.02629.
- [178].Menze BH et al. , “The multimodal brain tumor image segmentation benchmark (BRATS),” IEEE Trans. Med. Imag, vol. 34, no. 10, pp. 1993–2024, October. 2015, doi: 10.1109/TMI.2014.2377694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [179].Zhang Y et al. , “Collaborative unsupervised domain adaptation for medical image diagnosis,” IEEE Trans. Image Process, vol. 29, pp. 7834–7844, 2020, doi: 10.1109TIP.2020.3006377. [Google Scholar]
- [180].Mahmood F, Chen R, and Durr NJ, “Unsupervised reverse domain adaptation for synthetic medical images via adversarial training,” IEEE Trans. Med. Imag, vol. 37, no. 12, pp. 2572–2581, December. 2018, doi: 10.1109/TMI.2018.2842767. [DOI] [PubMed] [Google Scholar]
- [181].Wernick MN, Yang Y, Brankov JG, Yourganov G, and Strother SC, “Machine learning in medical imaging,” IEEE Signal Process. Mag, vol. 27, no. 4, pp. 25–38, July. 2010, doi: 10.1109/MSP.2010.936730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [182].Kurakin A, Goodfellow IJ, and Bengio S, “Adversarial machine learning at scale,” in Proc. Conf. Track, Toulon, France, 2017, p. 17. [Google Scholar]
- [183].Papernot N, McDaniel P, Wu X, Jha S, and Swami A, “Distillation as a defense to adversarial perturbations against deep neural networks,” in Proc. IEEE Symp. Security Privacy (SP), May 2016, pp. 582–597, doi: 10.1109/SP.2016.41. [DOI] [Google Scholar]
- [184].Volpi R, Namkoong H, Sener O, Duchi JC, Murino V, and Savarese S, “Generalizing to unseen domains via adversarial data augmentation,” in Proc. 31st Adv. Neural Inf. Process. Syst, 2018, pp. 5334–5344. [Google Scholar]
- [185].Liu Z, Zhang J, Jog V, Loh P-L, and McMillan AB. (August. 2019). Robustifying Deep Networks for Image Segmentation. Accessed: May 14, 2020. [Online]. Available: http://arxiv.org/abs/1908.00656. [DOI] [PMC free article] [PubMed]
- [186].Antun V, Renna F, Poon C, Adcock B, and Hansen AC, “On instabilities of deep learning in image reconstruction and the potential costs of AI,” Proc. Nat. Acad. Sci. USA, May 2020, Art. no. 201907377, doi: 10.1073/pnas.1907377117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [187].Lee J-G et al. , “Deep learning in medical imaging: General overview,” Korean J. Radiol, vol. 18, no. 4, pp. 570–584, 2017, doi: 10.3348/kjr.2017.18.4.570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [188].Chartrand G et al. , “Deep learning: A primer for radiologists,” RadioGraphics, vol. 37, no. 7, pp. 2113–2131, November. 2017, doi: 10.1148/rg.2017170077. [DOI] [PubMed] [Google Scholar]
- [189].Koneènı J, McMahan HB, Yu FX, Richtárik P, Suresh AT, and Bacon D, “Federated learning: Strategies for improving communication efficiency,” presented at the 13th Neural Inf. Process. Syst. (NIPS), Barcelona, Spain, 2016, Accessed: Aug. 06, 2020. [Online]. Available: http://arxiv.org/abs/1610.05492. [Google Scholar]
- [190].Domingos P, de Freitas N, Guyon I, Malik J, and Neville J. Plenary Panel: Is Deep Learning the New 42? Accessed: May 13, 2020. [Online]. Available: https://www.youtube.com/watch?v=furfdqtdAvc
- [191].Cortes C and Vapnik V, “Support-vector networks,” Mach. Learn, vol. 20, no. 3, pp. 273–297, September. 1995, doi: 10.1007/BF00994018. [DOI] [Google Scholar]
- [192].Ho TK, “Random decision forests,” in Proc. 3rd Int. Conf. Doc. Anal. Recognit vol. 1, August. 1995, p. 278. [Google Scholar]


