Diffusion Tensor Fiber Tractography of the Optic Radiation: Analysis with 6-, 12-, 40-, and 81-Directional Motion-Probing Gradients, a Preliminary Study

Abstract

BACKGROUND AND PURPOSE: Knowing the exact location of the optic radiation preoperatively is important for surgery of the temporal lobe. We hypothesized that a greater number of motion-probing gradients (MPGs) would provide better results of diffusion tensor (DT) fiber tractography of the optic radiation. To test this hypothesis, this study evaluated differences in DT fiber tractography of the optic radiation under different MPG settings.

METHODS: DT images were obtained in 12 healthy volunteers (7 men, 5 women) with a mean age of 32 years (range, 22–45 years) by using a 3T MR imaging scanner with single-shot echo-planar imaging with parallel acquisition (reduction factor = 2). MPG was applied in 6, 12, 40, and 81 independent directions. The first region of interest (ROI) was placed in the occipital lobe, and the second ROI was placed in the lateral geniculate body. Fibers penetrating both ROIs were considered as the optic radiation. Anteroposterior distance between the tip of the Meyer loop and the lateral geniculate body on an axial section was defined as a loop index. Numbers of fibers and loop indices in both cerebral hemispheres were evaluated statistically.

RESULTS: The optic radiation was well visualized in full length by DT fiber tractography in 20 of 24 hemispheres (83%). No significant differences were noted in number of fibers and loop indices among different MPG settings.

CONCLUSION: DT fiber tractography can frequently depict almost the entire optic radiation. MPG number does not exert any significant effect on visualization of the optic radiation, and 6-directional MPG is thus sufficient for this purpose.

Diffusion tensor (DT) imaging is an MR imaging technique that can be used to characterize the directional properties of the diffusion of water molecules.1,2 Application of this technique to the human brain has been demonstrated to provide exceptional information regarding white matter architecture.3,4 No other imaging techniques can provide equivalent information, so DT imaging is expected to become important for studying white matter anatomy and diagnosing various white matter abnormalities. Among the analyzing methods for DT imaging, DT fiber tractography has been reported as robust for visualizing and evaluating white matter fiber direction and connectivity in the brain.5–7

DT fiber tractography requires calculation of various parameters of a DT ellipsoid. Among these parameters, direction of the largest eigenvector (λ1), which is the direction of greatest diffusivity and generally assumed to align with the direction of fiber bundles, is the most important and indispensable for DT ellipsoid-based fiber tractography reconstruction methods.5,8 In DT ellipsoid-based fiber tractography, the path of a reconstructed fiber is determined by the direction of the largest eigenvector (λ1) in each voxel. The number of motion-probing gradients (MPGs) has been reported as an important factor for calculating DT parameters.9 However, to our knowledge, the MPG setting for optimal DT fiber tractography has not yet been determined.

The optic radiation arches anteriorly and laterally from the lateral geniculate body before coursing posteriorly to the occipital cortex. This curved course represents a challenge for DT fiber tractography, because white matter tracts of the temporal stem intermingle with other fibers that course in various directions and are indistinguishable from surrounding white matter on MR imaging.10 A recent article has reported that 3 layers of visual field trajectories were depicted by DT fiber tractography with a 32-MPG setting.11 Knowing the exact location of the optic radiation preoperatively is important for surgery of the temporal lobe.12 This information can be obtained exclusively by DT fiber tractography. However, to our knowledge, the appropriate number of MPGs for DT fiber tractography has not been decided.

We hypothesized that a greater number of MPGs would improve visualization of the optic radiation. To test this hypothesis, the present study evaluated differences in DT fiber tractography of the optic radiation under different MPG settings.

Methods

Subjects

Written informed consent was obtained from each volunteer, and all protocols for this prospective study were approved by the medical ethics committee of our institute. Data were obtained from 12 healthy volunteers (7 men, 5 women) with a mean age of 32 years (range, 22–45 years) and no history of neurologic injury or psychiatric disease. Subjects did not have any medication, drug, or alcohol history. No subjects displayed any neurologic signs or symptoms.

Data Acquisition

DT images were obtained by using a 3T MR imaging scanner (Magnetom Trio, Syngo MR 2004A, Siemens, Erlangen, Germany) with an 8-channel phased-array head coil by using single-shot echo-planar imaging with parallel acquisition (generalized autocalibrating partially parallel acquisitions; reduction factor = 2) in the axial plane. Imaging parameters were as follows: acquisition matrix, 96 × 96; FOV, 240 mm; section thickness, 2.5 mm; no intersection gap; 55 sections; TR, 6200–6300 ms; TE, 77–79 ms; b = 0, 700 seconds/mm². Reconstruction matrix was the same as the acquisition matrix, and 2.5 mm × 2.5 mm × 2.5 mm isotropic voxel data were obtained.

MPG was applied in 6, 12, 40, and 81 independent directions; the number of acquisitions was set at 13, 7, 2, and 1, respectively; the number of images was 5005, 5005, 4840, and 4950, respectively; and the acquisition time was 9 minutes 16 seconds, 9 minutes 25 seconds, 9 minutes 15 seconds, and 9 minutes 27 seconds, respectively. The number of signal intensity averages for b = 0 images was 13, 7, 8, and 9, respectively. Repeated acquisition of the b = 0 image is important for precise estimation of the tensor because variance of each of the elements of the tensor matrix should be minimized.13

Data Processing

DT imaging datasets were transferred to a workstation and processed by using DtiStudio, Version 2.3 software (H. Jiang, S. Mori; Johns Hopkins University, http://cmrm.med.jhmi.edu). All diffusion-weighted images were visually inspected by 2 authors for apparent artifacts due to subject motion and instrument malfunction, and no significant image deterioration was found. In our DT imaging dataset, there was low eddy-current–related geometric distortion between images obtained in each MPG direction; thus, postprocessing distortion correction was not applied for this dataset. Fractional anisotropy (FA) and color map images14 were calculated from diffusion-weighted images. DT fiber tractography was made by using the “fiber assignment by continuous tracking” method.5,15

Fiber Tract Reconstruction

Fiber tract reconstruction used a start and stop FA threshold of 0.25,16 according to the FA threshold of 0.25–0.35 for fiber tract reconstruction recommended by Mori et al16 and Stieltjes et al.17 We also used an inner product stop threshold of 0.34, prohibiting angles of >70° during tracking.18 A relatively large angle threshold was used so that the optic radiation coursing in an acute angle at the Meyer loop could be reconstructed. To reconstruct tracts of the optic radiation, we used a multiple region-of-interest (ROI) approach to exploit existing anatomic knowledge of tract trajectories.19 This method has low sensitivity to the ROI size and location and is highly beneficial for reproducible reconstruction of prominent white matter tracts with known trajectories.19 When multiple ROIs were used for a tract reconstruction, we used 3 types of operations: AND, OR, and NOT. Choice of operations depended on the characteristic trajectory of the tract.6

The first ROI was placed in the occipital lobe on a reconstructed coronal image with an OR operation, and after we placed the first ROI, the fibers penetrating this region were shown on axial, coronal, and sagittal images. The second ROI was manually placed in the lateral geniculate body on a reconstructed sagittal image with an AND operation. When we placed the second ROI, fibers penetrating the first ROI were already shown on a reconstructed sagittal image, so we could see a bundle of fibers penetrating the first ROI and the lateral geniculate body on a sagittal image. The second ROI could be placed on the lateral geniculate body with that fiber bundle as a landmark for the precise location. This 2-ROI method is relatively easy, and there is no variability that will bias the fiber tracking results.19 Reconstructed fibers penetrating both ROIs were considered representative of the optic radiation. FA values in both ROIs were measured by a function of DtiStudio software and analyzed statistically if there was any difference in FA values among different MPG settings by using analysis of variance. If there was significant difference, a t test was used for each pair comparisons.

For evaluating signal-to-noise ratio (SNR) of the diffusion-weighted images, we used the following formula20:

SNR = (0.66 × mean signal intensity) / (average of noise region standard deviations).

A large ROI (>2000 pixels) for signal intensity was placed in the brain tissue on an axial section containing the optic radiation. Four relatively small ROIs (144 pixels) for noise were placed in the background (air) at the 4 corners on the same section. This measurement was repeated throughout all the diffusion-weighted images, and we calculated the average value of SNR for each MPG setting. SNR differences among different MPG settings were evaluated statistically by using analysis of variance.

Fiber Tractography Analysis

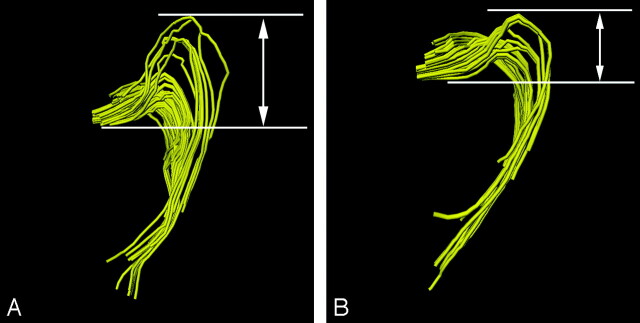
For analyzing the course and location of the reconstructed optic radiation, we evaluated the Meyer loop because it is the most characteristic part of the optic radiation and its curved course was considered to be a challenge for diffusion tensor fiber tractography.10 Anteroposterior distance between the anterior tip of the Meyer loop and the posterior end of the lateral geniculate body on an axial section was defined as a loop index (Fig 1). The loop index was considered to represent the course and location of the Meyer loop. Difference in the loop index among different MPG numbers was evaluated statistically by using analysis of variance.

Fig 1.

The anteroposterior distance between the tip of the Meyer loop and the lateral geniculate body on an axial section was defined as a loop index. Examples of loop index (A and B) are shown.

In addition to analyzing its shape, we counted the number of fibers in the optic radiation for both cerebral hemispheres by a function of DtiStudio software, and any difference due to MPG number was evaluated statistically by using a generalized linear mixed model, which is an extension of analysis of variance and regression analysis and has also been widely used in life science.21 For the all statistical evaluations, values of P < .05 were considered significant.

Results

FA value in the first ROI in the occipital lobe showed 0.29 ± 0.028 in 6 MPG, 0.26 ± 0.025 in 12 MPG, 0.26 ± 0.029 in 40 MPG, and 0.26 ± 0.039 in 81 MPG (values are mean values of 24 hemispheres ± SD). The FA value in the first ROI placed at the 6-MPG setting was significantly higher than that at other 3 MPG settings (P = .0007).

The FA value in the second ROI placed in the lateral geniculate body showed 0.39 ± 0.03 at 6 MPG, 0.35 ± 0.037 at 12 MPG, 0.35 ± 0.052 at 40 MPG, and 0.38 ± 0.071 at 81 MPG. The FA value in the second ROI at the 6-MPG setting was significantly higher than that at 12- and 40-MPG settings, and the FA value in the second ROI at the 81-MPG setting was significantly higher than that at the 40-MPG setting (P = .002).

SNR for each MPG setting showed 30.8 ± 2.28 at 6 MPG, 30.6 ± 1.80 at 12 MPG, 30.1 ± 1.90 at 40 MPG, and 30.0 ± 1.29 at 81 MPG. There was no significant difference in SNR value among different MPG settings (P = .708).

The loop index (anteroposterior distance between the anterior tip of the Meyer loop and the posterior end of the lateral geniculate body) was 16.2 ± 5.38 at 6 MPG, 20.5 ± 7.69 at 12 MPG, 17.7 ± 7.03 at 40 MPG, and 16.5 ± 6.91 at 81 MPG. There was no significant difference in loop index among different MPG settings (P = .13).

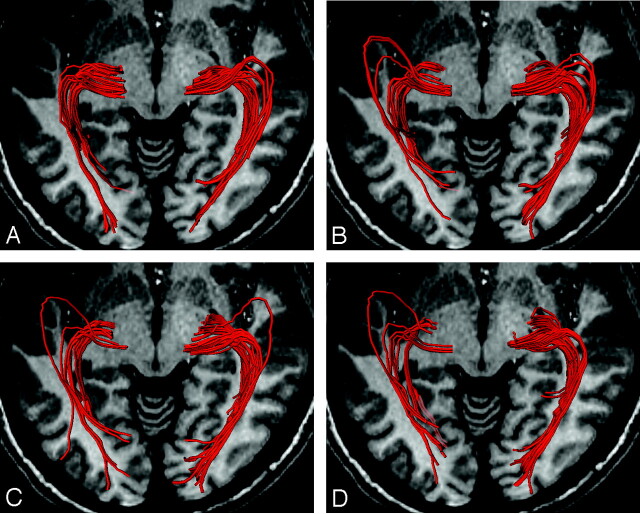
The optic radiation was well visualized along the full length by DT fiber tractography in 20 of 24 hemispheres (83%). No significant differences in number of fibers were noted among 6-, 12-, 40-, and 81-MPG settings (Fig 2) (P = .53; 6 MPG, 25.7 ± 23.0; 12 MPG, 32.8 ± 29.3; 40 MPG, 27.7 ± 24.0; 81 MPG, 24.3 ± 20.6).

Fig 2.

Reconstructed diffusion tensor fiber tractography of the optic radiation by using 6-MPG (A), 12-MPG (B), 40-MPG (C), and 81-MPG (D) settings.

Discussion

In this study, the optic radiation was well visualized along the full length by DT fiber tractography in 20 of 24 hemispheres (83%). Contrary to our hypothesis, MPG number did not exert any significant effect on visualization of the optic radiation. This study is the first to analyze the relationship between DT fiber tractography of the optic radiation and MPG number.

The largest eigenvector (λ1), indicating the direction of greatest diffusivity, is generally assumed to align with the direction of fiber bundles and thus represents an indispensable parameter for DT ellipsoid-based fiber tractography.5,8 In an estimation of DT parameters, 30 independent directional MPGs have been reported as desirable for analysis of diffusivity, and 20 independent directional MPGs have been reported as desirable for analysis of anisotropy.9 For calculation of DT parameters, particularly eigenvector, a smaller MPG number may introduce directional biases and reduced directional precision, whereas a larger MPG number can introduce more robust tensor ellipsoid estimation.9,22–24 The minimal mathematic requirement for DT calculation is 6 independent directional MPG settings, and this may allow relatively short imaging time. Conversely, settings like 40 or 81 independent MPGs may involve relatively longer imaging times. However, the amount of imaging time is limited in most clinical situations. Choice of MPG settings thus involves a trade-off between minimizing directional bias and minimizing scanning time.

As many unique directional MPGs as time will allow should reportedly be used for fiber tractography according to a Monte Carlo simulation approach.9 However, in this actual human brain study, differences due to MPG number in DT fiber tractography of the optic radiation were not particularly prominent. Various reasons might underlie this finding. First, the issue of SNR is important in DT fiber tractography19 and may not be negligible. In the present study, SNR values did not show any significant difference among different MPG settings, so SNR effect of different MPG settings on the results of fiber tractography in the present study can be considered negligible. Second, the multiple ROI approach was used in the present study, and this method has been reported to be robust for studying prominent tracts with known trajectories and low sensitivity to the ROI size and location.19 The 2 ROI approach is a very strong analyzing method and it can make the difference of the fiber tractography obscure among the different MPG numbers. Third, we evaluated the optic radiation only and did not evaluate other fiber tracts such as the corticospinal tract. Anatomic features of the optic radiation fibers may have had some effect on the results of DT fiber tractography in this study and may have cancelled any positive effect of larger MPG numbers.

Factors affecting SNR in DT imaging include the number of signal intensity averaging, MPG number, and encoding levels.25 In the present study, b = 0 images were obtained repeatedly for precise estimation of the tensor because variance of each of the elements of the tensor matrix should be minimized.13 Low SNR may result in variance of each of the tensor elements and, finally, in overestimating FA value26; thus, it will change DT parameters for fiber tractography. With the issue of SNR for DT parameter calculation, number of signal-intensity averaging and number of MPGs should be considered differently. A previous article reported that an increasing MPG number decreases error in DT parameter calculation more than the number of signal intensity averaging does.27 In this study, FA values of ROIs for fiber reconstruction were significantly higher in the 6-MPG setting than those of other MPG settings. This higher FA value may partly reflect an error of DT parameter calculation because of the smaller MPG number as shown in previous reports.13,27 Although there might have been an FA value calculation error in the smaller MPG setting, the results of fiber tractography showed no significant difference in the present study. We thus assume that the MPG number may be significant for DT parameter calculation; however, the effect of the MPG number for visualization of the optic radiation was insignificant in the present study.

The optic radiation arches anteriorly and laterally from the lateral geniculate body before coursing posteriorly to the occipital cortex. This curved course represents a challenge for DT fiber tractography, because white matter tracts of the temporal stem intermingle with other fibers that course in various directions and are indistinguishable from the surrounding white matter on MR imaging studies.10,11 Knowing the exact location of the optic radiation preoperatively is important for surgery of the temporal lobe.12 In this study, DT fiber tractography depicted the optic radiation along almost the entire length in 83% of cases, irrespective of MPG number. DT imaging is noninvasive and is the only known method for gaining directional information on white matter of the brain.3,4 This imaging method may contribute to preoperative planning and intraoperative evaluation for temporal and occipital lobe surgery. DT imaging may be feasible for surgical therapy of temporal lobe epilepsy, brain tumors, and other lesions in the brain near the optic radiation.28

Multidirectional MPG settings have been used as an efficient evaluation method for determining intravoxel white matter fiber heterogeneity, such as Q-ball imaging for analysis of intravoxel fiber crossing.29–31 In addition to these analyses, for the probabilistic DT fiber reconstruction approach, as large an MPG number as time will allow has been reported as necessary.9 In these analytic methods, larger MPG numbers may have merit and be indispensable for effective analysis.

This study has several limitations. First, only a limited number of subjects were enrolled into this preliminary study. A larger number should be enrolled in a future study. Second, only the optic radiation was evaluated. Other neuronal fiber bundles such as the corticospinal tract or superior longitudinal fascicles could be evaluated in future studies. Third, we evaluated the optic radiation only by the DT ellipsoid-based fiber tractography method with 1 threshold value setting. Further study is needed for evaluation of other fiber-reconstruction approaches such as the probabilistic approach32 and for the effects of changing threshold values in the DT ellipsoid-based fiber tractography method. Fourth, we did not evaluate differences in various MPG spatial-distribution schemes. Further study is needed for evaluation of other MPG schemes.

Conclusion

In conclusion, DT fiber tractography can frequently depict the optic radiation along almost the entire length. MPG number does not exert a significant difference for visualization of the optic radiation in the equal SNR setting, and 6-directional MPG is sufficient for visualization of this structure.