Abstract.
Purpose: To validate a previously proposed algorithm that modifies a mammogram to appear as if it was acquired with different technique factors using realistic phantom-based mammograms.
Approach: Two digital mammography systems (an indirect- and a direct-detector-based system) were used to acquire realistic mammographic images of five 3D-printed breast phantoms with the technique factors selected by the automatic exposure control and at various other conditions (denoted by the original images). Additional images under other simulated conditions were also acquired: higher or lower tube voltages, different anode/filter combinations, or lower tube current–time products (target images). The signal and noise in the original images were modified to simulate the target images (simulated images). The accuracy of the image modification algorithm was validated by comparing the target and simulated images using the local mean, local standard deviation (SD), local variance, and power spectra (PS) of the image signals. The absolute relative percent error between the target and simulated images for each parameter was calculated at each sub-region of interest (local parameters) and frequency (PS), and then averaged.
Results: The local mean signal, local SD, local variance, and PS of the target and simulated images were very similar, with a relative percent error of 5.5%, 3.8%, 7.8%, and 4.4% (indirect system), respectively, and of 3.7%, 3.8%, 7.7%, and 7.5% (direct system), respectively.
Conclusions: The algorithm is appropriate for simulating different technique factors. Therefore, it can be used in various studies, for instance to evaluate the impact of technique factors in cancer detection using clinical images.
Keywords: digital mammography, virtual clinical trials, image quality, image simulation
1. Introduction
Currently, digital mammography is the predominant examination used for breast cancer screening, allowing for early breast cancer detection.1 However, breast cancer detection performance can be affected by the quality of the mammogram.2–4 Therefore, evaluation and optimization of image quality is very important to maximize the performance of mammographic screening.5,6
There are several factors to be considered when evaluating the performance of a digital mammography system that can affect the image quality: detector type, technique factors, modulation transfer properties (spatial resolution), and dose level. The sub-optimal selection or behavior of any of these factors can result in a loss of resolution and/or contrast and in an increase in noise in the resulting image.3,4,7–9
Ideally, testing the impact of acquisition factors on the detection performance of radiologists would be performed with clinical images, using resource and labor-intensive studies, such as receiver operating characteristic (ROC)-based observer studies.10–12 However, it is not feasible to perform ROC studies to test the effect of varying even a few factors, since either a large number of images of different clinical cases would be needed or the images of these same cases would need to be acquired with different values of factors, which would be unethical.13 Therefore, alternative methods, such as virtual clinical trials (VCTs),14 are being introduced for image quality evaluation, reducing the cost and duration of studies and the need for repeated radiation exposure of subjects. VCTs include simulations of the breast and lesions, and of the processes of image formation and interpretation. The image formation processes entail image acquisition and processing.14 For this, VCTs use images and lesions simulated using mathematical models15–18 or modified real mammograms.19–21 The former require, in many cases, virtual phantoms that are a realistic representation of breasts.22 However, virtual phantoms still do not sufficiently and realistically represent the variety of anatomy, shape, density, and thickness, nor the variety of lesion types, found clinically. An alternative is to use real mammograms that are modified in ways that represent the impact of variations in the factors to be studied.23–25 In addition, several methods to simulate variations of dose levels and/or resolution have been undertaken.23–27 The basic principle of reducing the dose level of an image is to add to the image a realistic, frequency-dependent simulation of image noise. The resulting simulated noise should match both magnitude of noise in the target image and the noise power spectra (NPS). It is also possible to adjust the sharpness of the images to match the expected modulation transfer function of the target image.23–27 These methods apply the change globally to an image and do not account for the spatial dependence changes required for simulating images as if acquired using different tube voltages and anode/filter combinations.23–27
Previously, an algorithm was proposed by Mackenzie et al.24,25 to modify real mammograms so that they appear as if acquired with a lower tube current–time product (reducing the dose level of the image) and/or with different image receptors (different spatial resolution conditions), scatter-to-primary ratios (SPR), glare-to-primary ratios (GPR), and grid factors. An extension to this algorithm, which accounts for changes in tube voltage and anode/filter combination, was later proposed.28 These algorithms were validated using simple test objects, such as homogeneous slabs24,25,28 and breast phantoms.29,30 The algorithms were found to be able not only to simulate different levels of quantum noise but also to correctly change the contrast within an image. However, to be able to use these algorithms for future clinical image quality evaluation studies, it is important to validate this modification model more comprehensively. First, these algorithms need to be tested for a larger variation of imaging conditions, including failure modes, e.g., when the imaging system uses too low an acquisition dose. Second, the validity of the algorithm when applied to images of breasts that span the large range of breast thicknesses and compositions that may be encountered in the clinic also needs to be verified.
Therefore, the aim of this work is to validate an image modification algorithm for a variety of breasts and imaging conditions using realistic mammograms produced from various 3D-printed breast phantoms of varying thickness and breast composition.
2. Methods
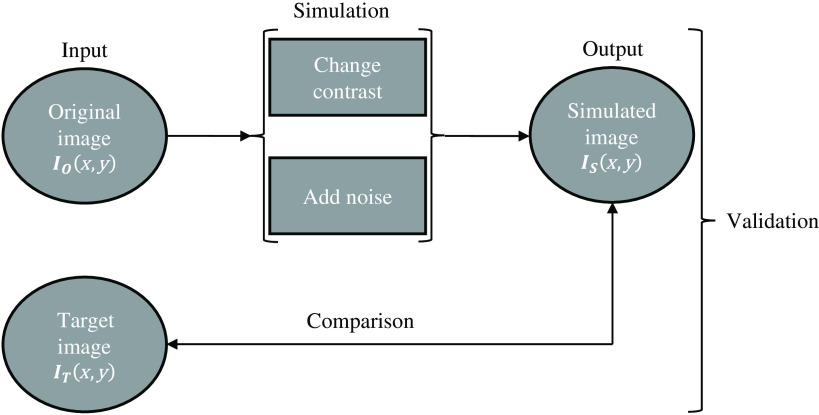
In this study, an algorithm that simulates images acquired at different technique factors was validated using realistic images obtained with 3D-printed breast phantoms. For this, an input image, the original image (, was acquired with specific acquisition conditions, resulting in a given level of noise, contrast, etc. This image was used to simulate several different, lower quality, simulated images (, i.e., the output images of the image modification process as if they had been acquired with different acquisition conditions, resulting in a higher relative noise and/or lower/higher contrast, etc. The algorithm was validated by comparing these simulated images with images actually acquired at the lower quality settings, denoted as target images (. Figure 1 presents a brief overview of the described methodology. This modification process was applied to “for processing” images.
Fig. 1.
Workflow of the image modification process and respective validation applied to “for processing” images.
2.1. Image Modification Algorithm
This study aims to validate a previously developed algorithm that simulates the acquisition of mammographic images with different image receptors or technique factors (anode/filter combination, tube voltage, and tube current–exposure time product), resulting in changes in contrast or noise. This image modification algorithm, in turn, is an extension of another algorithm that modifies images to appear as if they were acquired with a lower tube current–time product but keeping the other technique factors constant (anode/filter combination and tube voltage).24,25 The new version allows for not only a global change in signal statistics, as in the original algorithm but also a change in these that is spatially dependent. This means that the simulation of images as if acquired with a lower tube current–exposure time product only changes the entire image equally. On the other hand, the simulation of images as if acquired using different tube voltage and/or anode/filter combinations introduces changes in the image that are spatially variant.28 The completed algorithm, previously described fully in the respective original publications,24,25,28 can be briefly described as follows.
First, the image is linearized such that all pixel values (PVs) of the original image are directly proportional to the absorbed energy per unit area in the detector () so that the signal in the image is a function of . The change in signal between the original and the target images is calculated by taking into account the attenuation of all of the objects in the beam, including the breast phantom or different breast tissues, given the original and target technique factors, spectra, radiation output, and air kerma to absorbed energy per unit area conversion. Using the knowledge of all of the attenuation coefficients together with the grid factor and SPR and GPR factors of both the original and target images, a thickness map is obtained from the original images. In the case of a breast phantom, the attenuation values correspond to those of the phantom material, with the phantom considered to be composed of a single tissue. In the case of a real breast, the attenuation values correspond to the different tissues in the breast, such as glandular and adipose tissue. In the thickness map, each PV corresponds to the thickness of the breast phantom or of the different breast tissues. Once this thickness map is estimated, the signal in the original image can be adjusted by calculating a map of the ratio of the signal between the target and the original images that accounts for the differences in signal between the two images.
Following the application of the signal ratio to the original image, noise needs to be added to this image to match that of the target image. The noise model calculates the total NPS present in each image by considering the different types of noise within the image (electronic, quantum, and structure) and by estimating a quantum noise factor correction. In this stage, differences in scatter are also considered.25,28
2.2. Application and Validation of the Modification Algorithm
To be able to use and validate the algorithm, a complete characterization of the mammography systems was performed, breast phantom images were acquired, and image comparison metrics were applied.
2.3. Mammography System Characterization
Two digital mammography systems were used for this validation: a Senographe Essential (GE Healthcare, Buc, France), with an indirect detector, and a Lorad Selenia (Hologic, Inc., Bedford, Massachusetts), with a direct detector. The systems were characterized in terms of first half value layer (HVL); signal transfer properties (STP) and absorbed energy per unit area per incident air kerma (); grid factor; flat-field correction; NPS to calculate the noise model; and glare and scatter properties.
All of these parameters were measured and calculated as previously described and according to respective guidelines, 24,25,31–36 with the algorithms and results described in detail in the Appendix (Sec. 6).
2.4. Breast Phantoms
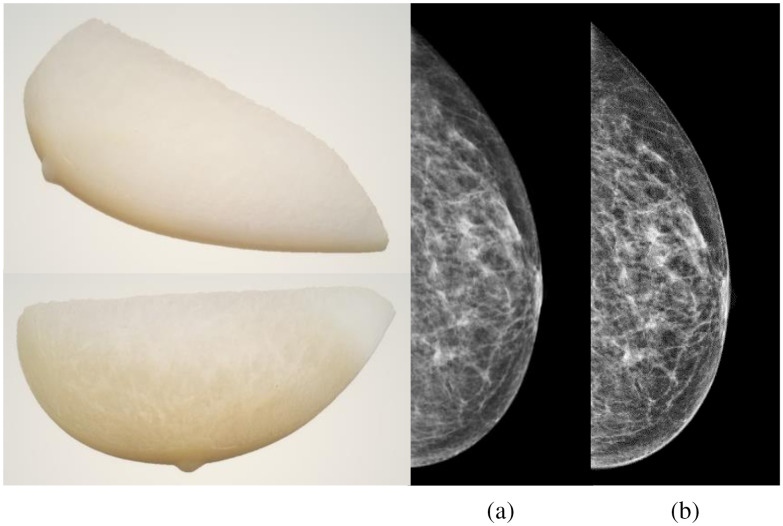
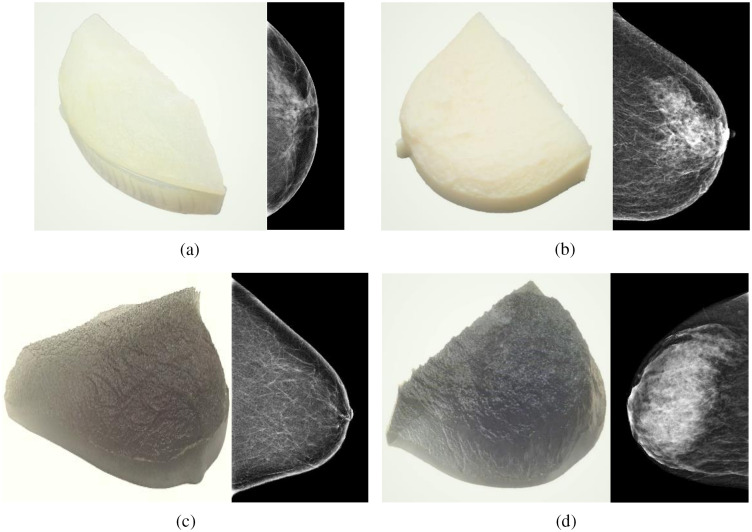
Five patient-based 3D-printed breast phantoms37 developed by the Institute of Medical Physics and Radiation Protection from the Technische Hochschule Mittelhessen (IMPS, Gießen, Germany) were used to validate and evaluate the performance of the image modification algorithm. The phantoms, shown in Figs. 2 and 3, were printed using a 3D-printer (Objet 30 Pro, Stratasys, Eden Prairie, Minnesota) with three phantoms printed using the polypropylene-like material, Rigur RGD450™, and two phantoms using the transparent PolyJet™ photopolymer PMMA-like material, VeroClear™. These phantoms result in images with realistic anatomical structures and attenuation characteristics and are based on anonymized patient mammograms from breasts with a range of breast glandular densities.37 The compressed breast thickness of the real breasts was 42, 57, 32, 63, and 76 mm for the phantoms nominally called “Anna,” “Barbara,” “Chris,” “Diana,” and “Elizabeth,” respectively.
Fig. 2.
(left side) 3D-printed breast phantom Anna. (right side) Comparison between the (a) phantom mammogram and (b) real mammogram.
Fig. 3.
(left) Photograph of the 3D-printed breast phantom with realistic patient tissue distribution, and (right) corresponding mammogram for (a) Barbara phantom (due to printer memory issues, corresponding to only a section of the whole mammogram), (b) Chris phantom, (c) Diana phantom, and (d) Elizabeth phantom.
The phantom design is based on a method that aims to reproduce real patient two-dimensional mammograms by replicating the respective x-ray attenuation at each pixel by varying the thickness of the phantom across its surface.38 The thickness of each phantom projecting to each pixel in the mammogram is calculated by estimating the amount of x-ray attenuation at each pixel of the corresponding patient mammogram and using the knowledge of the imaging system parameters, such as x-ray spectrum, detector response function, etc. In this way, the resulting phantom images closely resemble the corresponding patient images.
2.5. Validation
The validation of the modification algorithm was undertaken by acquiring images of each of the five phantoms at both the original and target imaging conditions and comparing the latter with the simulated images. These comparisons were performed on “for processing” images only.
2.5.1. Image acquisition
The images of the five 3D-printed breast phantoms positioned on the breast support were acquired using the GE and Hologic mammography systems previously characterized. For the image acquisition, first the automatic exposure control (AEC) of each system was used to determine the acquisition parameters used for each phantom. Then, additional phantom images were acquired with other technique factors, as listed in Table 1 (GE) and Table 2 (Hologic), to be used as original and target images. The factors were selected according to what degradation type or level of degradation was intended to be simulated and considering that the target images must have a lower image quality than the original image. For each phantom and for each system, three images per condition were acquired. For the series of images acquired, the phantom was not moved.
Table 1.
Technique factors used for image acquisition with the respective breast phantom for the GE system, aiming to vary either tube voltage or tube current–time product. Only the factors that were modified between the original and target images are listed in the two right-most columns.
| Breast phantom | Technique factors of original images | Technique factors of target images with different tube voltages | Technique factors of target images with lower tube current–time product |
|---|---|---|---|
| Anna | Mo/Mo, 26 kV, 45 mAsa | 22 kV, 70 mAs | 22.5 mAs |
| 24 kV, 50 mAs | 11 mAs | ||
| Mo/Mo, 26 kV, 90 mAs | 28 kV, 40 mAs | — | |
| 30 kV, 28 mAs | — | ||
| Mo/Mo, 22 kV, 140 mAs | — | 70 mAs | |
| Mo/Mo, 30 kV, 56 mAs | — | 28 mAs | |
| Barbara | Rh/Rh, 29 kV, 45 mAsa | 25 kV, 80 mAs | 22.5 mAs |
| 27 kV, 56 mAs | 11 mAs | ||
| Rh/Rh, 29 kV, 90 mAs | 31 kV, 36 mAs | — | |
| 33 kV, 25 mAs | — | ||
| Rh/Rh, 25 kV, 160 mAs | — | 80 mAs | |
| Rh/Rh, 33 kV, 50 mAs | — | 25 mAs | |
| Chris | Mo/Mo, 27 kV, 50 mAsa | 23 kV, 36 mAs | 25 mAs |
| 25 kV, 63 mAs | 12.5 mAs | ||
| Mo/Mo, 27 kV, 100 mAs | 29 kV, 45 mAs | — | |
| 31 kV, 36 mAs | — | ||
| Mo/Mo, 23 kV, 70 mAs | — | 36 mAs | |
| Mo/Mo, 31 kV, 70 mAs | — | 36 mAs | |
| Diana | Rh/Rh, 29 kV, 63 mAsa | 25 kV, 80 mAs | 32 mAs |
| 27 kV, 70 mAs | 16 mAs | ||
| Rh/Rh, 29 kV, 125 mAs | 31 kV, 56 mAs | — | |
| 33 kV, 25 mAs | — | ||
| Rh/Rh, 25 kV, 160 mAs | — | 80 mAs | |
| Rh/Rh, 33 kV, 50 mAs | — | 25 mAs | |
| Elizabeth | Rh/Rh, 30 kV, 110 mAsa | 26 kV, 70 mAs | 56 mAs |
| 28 kV, 125 mAs | 28 mAs | ||
| Rh/Rh, 30 kV, 225 mAs | 32 kV, 100 mAs | — | |
| 34 kV, 45 mAs | — | ||
| Rh/Rh, 26 kV, 140 mAs | — | 70 mAs | |
| Rh/Rh, 34 kV, 90 mAs | — | 45 mAs |
The ones that were selected by the AEC for that phantom.
Table 2.
Technique factors used for image acquisition with the respective breast phantom for the Hologic system, aiming to vary either tube voltage, and, in some cases, anode/filter combination, or tube current–time product. Only the factors that were modified between the original and target images are listed in the two right-most columns.
| Breast phantom | Technique factors of original images | Technique factors of target images with different tube voltages | Technique factors of target images with lower tube current–time product |
|---|---|---|---|
| Anna | W/Rh, 26 kV, 70 mAsa | 22 kV, 120 mAs | 35 mAs |
| 18 mAs | |||
| W/Rh, 26 kV, 140 mAs | 28 kV, 50 mAs | — | |
| 30 kV, 35 mAs | — | ||
| W/Rh, 22 kV, 240 mAs | — | 120 mAs | |
| W/Rh, 30 kV, 70 mAs | — | 35 mAs | |
| Barbara | W/Rh, 28 kV, 110 mAsa | 24 kV, 120 mAs | 55 mAs |
| 28 mAs | |||
| W/Rh, 28 kV, 220 mAs | 30 kV, 80 mAs | — | |
| 32 kV, 65 mAs | — | ||
| W/Ag, 30 kV, 50 mAs | — | ||
| W/Ag, 32 kV, 40 mAs | — | ||
| W/Rh, 24 kV, 240 mAs | — | 120 mAs | |
| W/Rh, 32 kV, 130 mAs | — | 65 mAs | |
| W/Ag, 32 kV, 80 mAs | — | 40 mAs | |
| Chris | W/Rh, 27 kV, 85 mAsa | 23 kV, 110 mAs | 42.5 mAs |
| 22 mAs | |||
| W/Rh, 27 kV, 170 mAs | 29 kV, 60 mAs | — | |
| 31 kV, 50 mAs | — | ||
| W/Rh. 23 kV, 220 mAs | — | 110 mAs | |
| W/Rh, 31 kV, 100 mAs | — | 50 mAs | |
| Diana | W/Rh, 29 kV, 120 mAsa | 25 kV, 140 mAs | 60 mAs |
| 27 kV, 140 mAs | 30 mAs | ||
| W/Rh, 29 kV, 240 mAs | 31 kV, 95 mAs | — | |
| 33 kV, 70 mAs | — | ||
| W/Ag, 33 kV, 42.5 mAs | — | ||
| W/Rh, 25 kV, 280 mAs | — | 140 mAs | |
| W/Rh, 33 kV, 140 mAs | — | 70 mAs | |
| W/Ag, 33 kV, 80 mAs | — | 42.5 mAs | |
| Elizabeth | W/Ag, 30 kV, 150 mAsa | 26 kV, 80 mAs | 75 mAs |
| 28 kV, 180 mAs | 37.5 mAs | ||
| W/Ag, 30 kV, 300 mAs | 32 kV, 120 mAs | — | |
| 34 kV, 85 mAs | — | ||
| W/Ag, 26 kV, 160 mAs | — | 80 mAs | |
| W/Ag, 34 kV, 170 mAs | — | 85 mAs |
The ones that were selected by the AEC for that phantom.
2.5.2. Image analysis
The local mean signal, local standard deviation (SD), local variance, and power spectra (PS) were used to verify the similarity between the target and simulated images by comparing the average PVs, the variation in PVs, and the frequency dependency of the image structures and noise, respectively. In addition, image subtraction was performed by evaluating the residual image resulting from subtracting the target and simulated phantom images, allowing for a comparison of the two images by measuring the noise that remains after the subtraction. Analysis between the original and simulated images was also performed as a control.
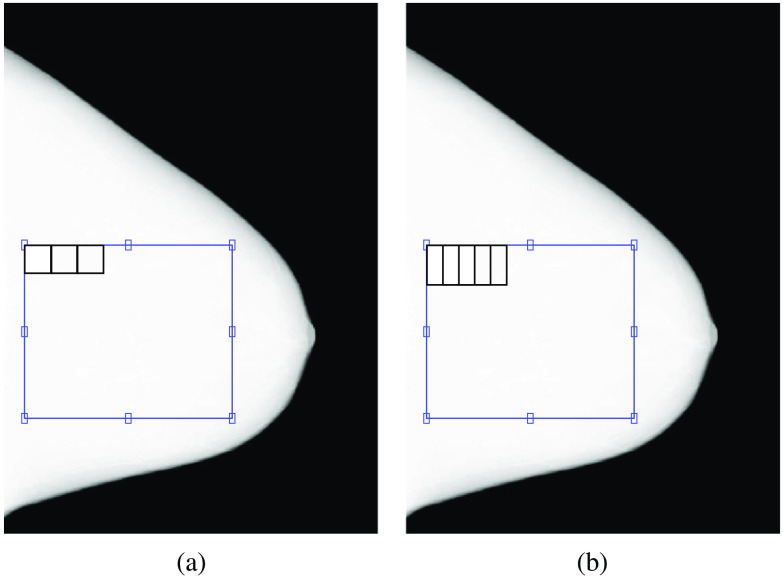
The local mean signal, local SD, local variance, and PS of a selected region of interest (ROI) in the center of the breast in the original, target, and simulated images, after linearizing them to absorbed energy per unit area, were calculated. The ROI selected was for Anna, for Barbara, for Chris, for Diana, and for Elizabeth for the GE and Hologic images (Fig. 4). The ROI size was adjusted to the phantom size. For the calculation of local mean signal, local SD, and local variance, the ROI was split into several non-overlapping sub-ROIs of , and these parameters were calculated in each sub-ROI. The final values are the average of each of the parameters of the three acquired or simulated images. For the calculation of PS, the ROI was split into several half-overlapping sub-ROIs of . The PS was calculated for each sub-ROI, and the final PS of each image was then the average of the PS of all sub-ROIs. The final PS is the average of the PS of the three acquired or simulated images. A 2D Hanning window was applied to each sub-ROI to avoid leakage effects from the Fourier transform.
Fig. 4.
Illustration of the ROI selection and respective (a) non-overlapping sub-ROIs for the calculation of local mean signal, local SD, and local variance and (b) half-overlapping sub-ROIs for the calculation of PS, for Diana images acquired with the GE system.
The relative percent error between the target and simulated images and between the original and simulated images for each parameter was calculated at each sub-ROI (local parameters) and frequency (PS). The final values correspond to the absolute average across the sub-ROIs and frequency. The respective 95% confidence interval (CI) was also calculated using statistical functions from MATLAB (version 2019a, The MathWorks, Inc., Natick, Massachusetts).
The ROI selected from the target image was also subtracted from the corresponding simulated image, and the ROI selected from the original image was subtracted from the corresponding simulated image.
3. Results
The results obtained from the characterization of GE and Hologic systems are included in Sec. 6. The results calculated to validate the image modification algorithm are included in this section.
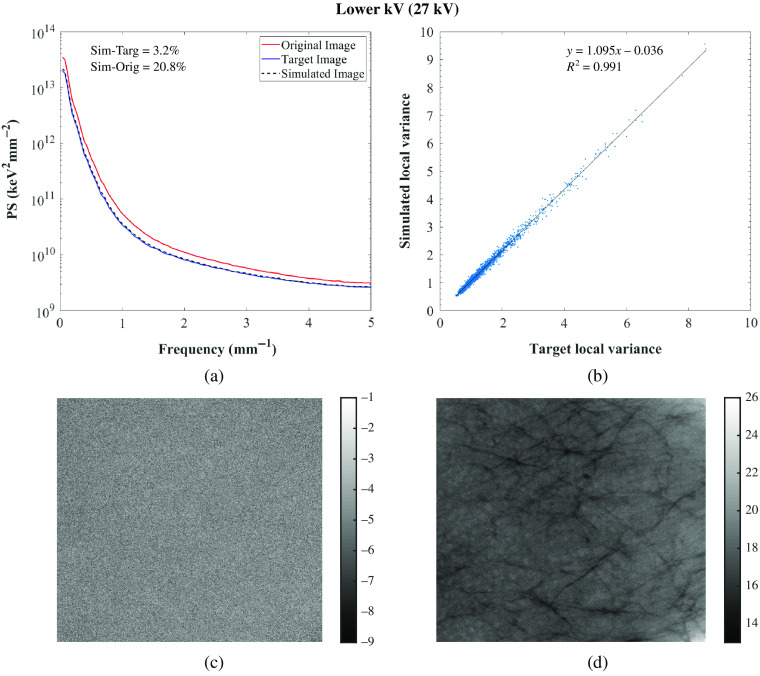
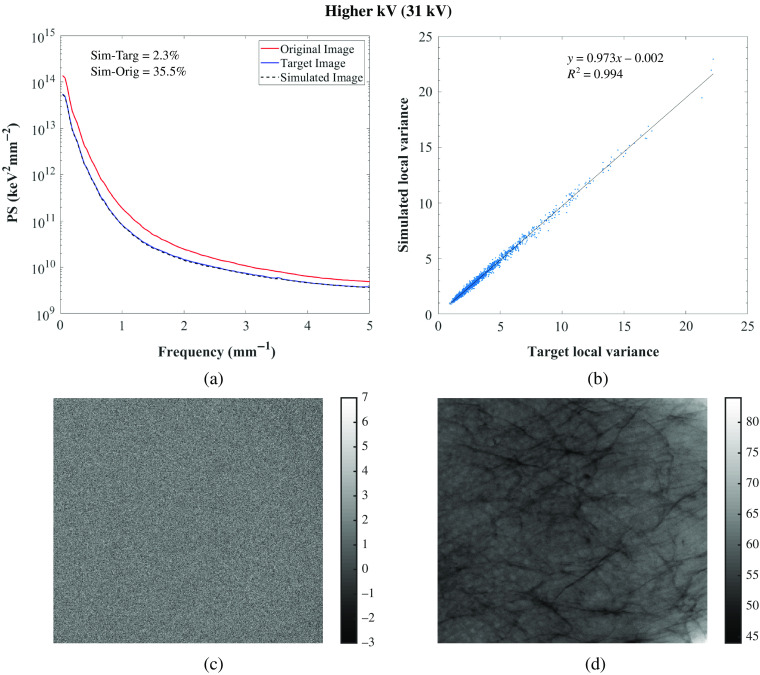
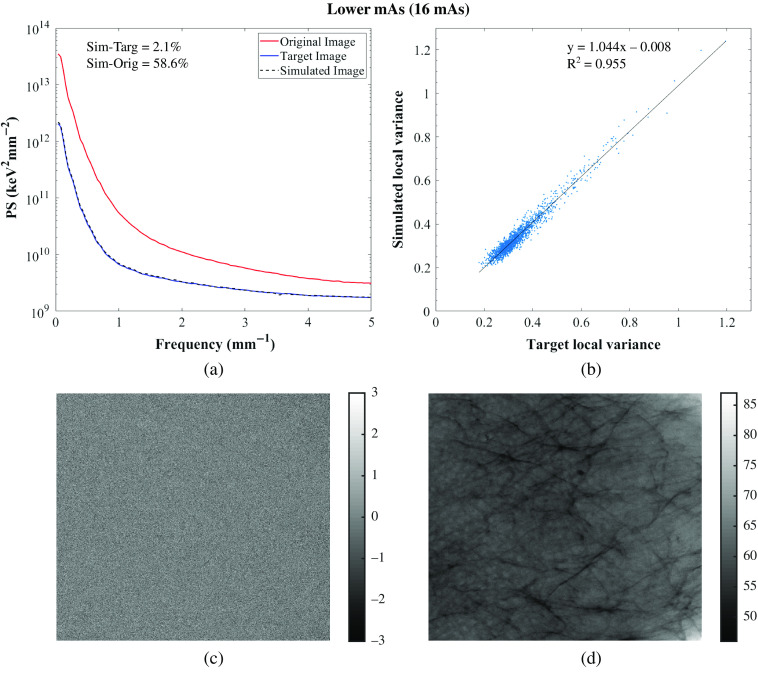
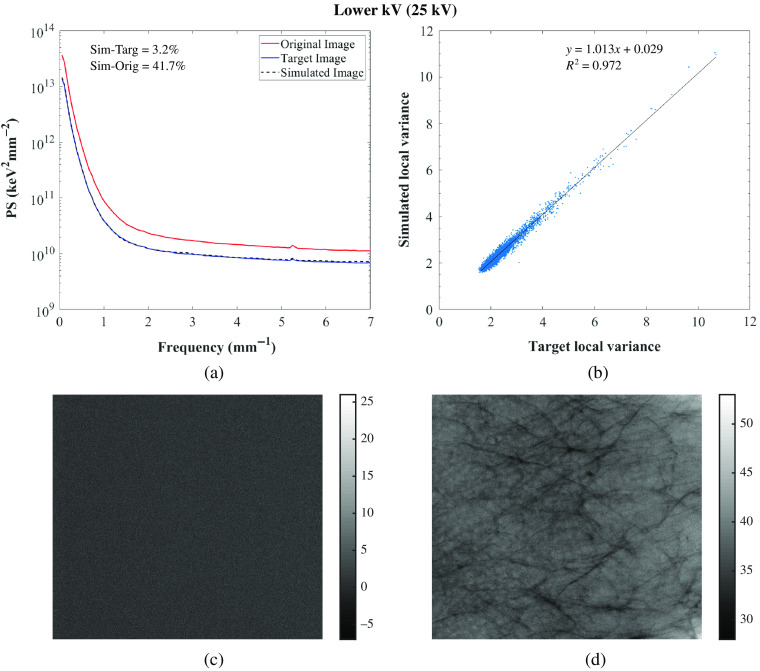
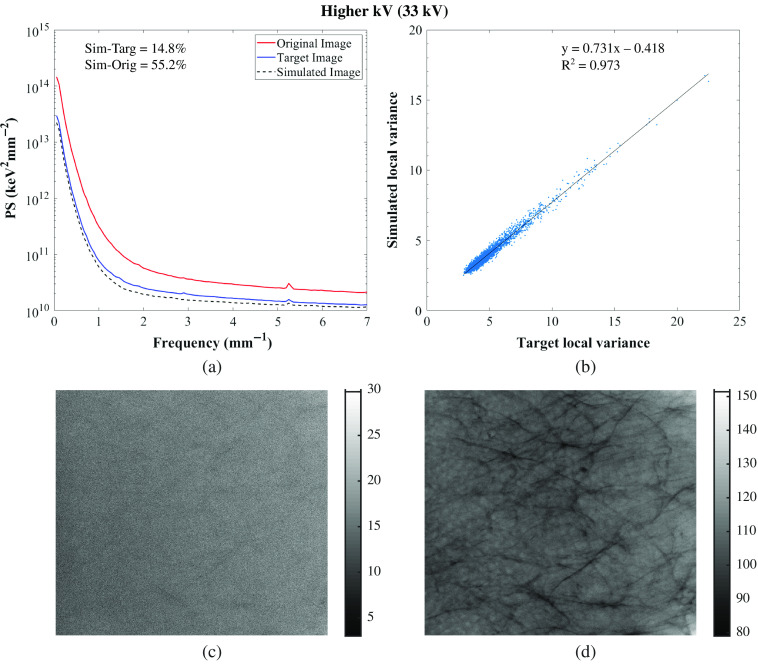
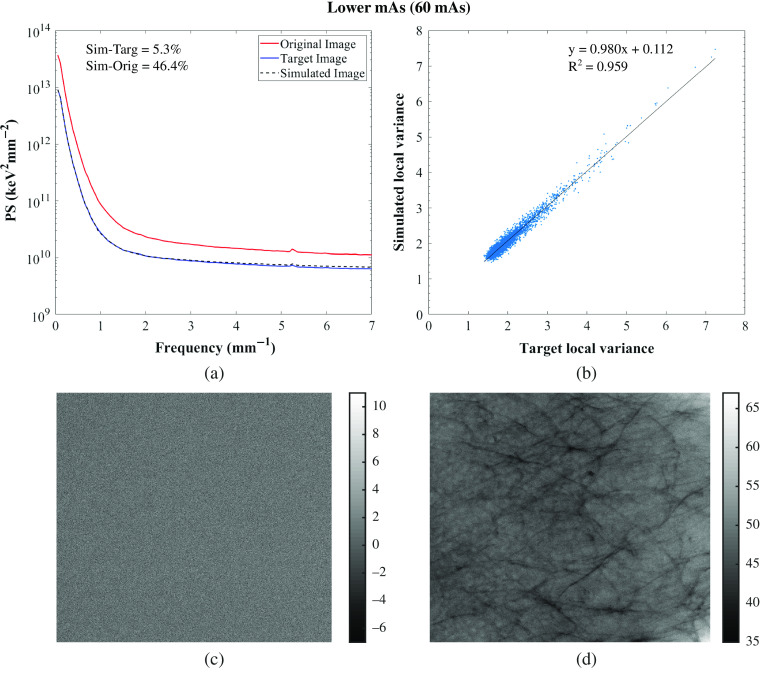
The relative percent error of the local mean signal, local SD, local variance, and PS calculated between the target and simulated images and between the original and simulated images are shown in Tables 3 and 4 for the GE system and in Tables 5 and 6 for the Hologic systems. Similarities between those images for the five phantoms were found with an average relative percent error across phantoms between the target and simulated images of the local mean signal, local SD, local variance, and PS of 5.5%, 3.8%, 7.8%, and 4.4%, respectively, for GE, and of 3.7%, 3.8%, 7.7%, and 7.5%, respectively, for Hologic. With the evaluated modification algorithm, images can only be degraded, so the targeted technique factors were chosen to result in images of lower quality than the original. The PS of the original, target, and simulated Diana (phantom that approximately resembles an average breast, in terms of thickness) images for one set of lower and higher tube voltage simulations and one lower tube current–time product simulation are shown in Figs. 5–7 for the GE system and in Figs. 8–10 for the Hologic system. The graphs show high similarity between the target and simulated images, since both PS match for all of the phantoms and systems. Also, the correlation between the local variance calculated for the target and simulated images is shown in Figs. 5–7 for the GE system and in Figs. 8–10 for the Hologic system, with respective identity line and correlation parameters. In all cases, the Pearson’s correlation coefficient is close to unity, while in all but one case the slope and offset of the linear fit are close to unity and zero, respectively.
Table 3.
Relative percent error of the local mean signal, local SD, local variance, and PS calculated between target and simulated images, and between original and simulated images, for the condition of lower and higher tube voltage simulation corresponding to each breast phantom for the GE system.
| Breast phantom | Original techniques factors | Anode/Filter | kV | mAs | Relative error (%) [95% CI] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean signal | SD | Variance | PS | |||||||||
| Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | |||||
| Anna | Mo/Mo, 26 kV, 45 mAs | Mo/Mo | 22 | 70 | 21.3 [21.3, 21.4] | 38.1 [38.1, 38.1] | 11.8 [11.4, 12.2] | 34.2 [34.0, 34.4] | 25.2 [24.3, 26.1] | 56.7 [56.4, 56.9] | 10.8 [9.2, 12.3] | 36.6 [34.5, 38.7] |
| 24 | 50 | 6.3 [6.3, 6.3] | 28.5 [28.5, 28.5] | 3.1 [2.9, 3.4] | 24.6 [24.5, 24.8] | 6.4 [6.0, 6.9] | 43.1 [42.9, 43.4] | 4.2 [3.7, 4.7] | 25.1 [23.3, 26.8] | |||
| Mo/Mo, 26 kV, 90 mAs | 28 | 40 | 2.7 [2.7, 2.7] | 34.8 [34.8, 34.8] | 1.7 [1.5, 1.8] | 34.1 [34.0, 34.2] | 3.3 [3.1, 3.6] | 56.5 [56.4, 56.7] | 3.9 [3.2, 4.5] | 33.2 [31.1, 35.2] | ||
| 30 | 28 | 4.7 [4.6, 4.7] | 36.1 [36.1, 36.1] | 1.8 [1.7, 2.0] | 36.3 [36.2, 36.5] | 3.6 [3.3, 3.9] | 59.4 [59.2, 59.6] | 4.3 [3.9, 4.8] | 32.8 [30.5, 35.2] | |||
| Barbara | Rh/Rh, 29 kV, 45 mAs | Rh/Rh | 25 | 80 | 21.7 [21.4, 21.9] | 19.1 [19.1, 19.1] | 9.6 [9.1, 10.0] | 17.6 [17.4, 17.7] | 20.3 [19.3, 21.2] | 32.0 [31.7, 32.2] | 7.0 [5.9, 8.0] | 24.5 [23.6, 25.5] |
| 27 | 56 | 8.7 [8.6, 8.8] | 12.4 [12.4, 12.4] | 4.0 [3.7, 4.3] | 11.2 [11.0, 11.3] | 8.2 [7.6, 8.8] | 21.1 [20.8, 21.3] | 4.9 [4.3, 5.5] | 13.9 [13.1, 14.7] | |||
| Rh/Rh, 29 kV, 90 mAs | 31 | 36 | 2.8 [2.8, 2.9] | 44.3 [44.3, 44.3] | 2.5 [2.3, 2.8] | 42.3 [41.9, 42.6] | 5.0 [4.5, 5.5] | 66.6 [66.2, 67.0] | 4.7 [4.2, 5.3] | 43.3 [41.3, 45.3] | ||
| 33 | 25 | 4.4 [4.3, 4.4] | 48.0 [47.9, 48.0] | 2.9 [2.6, 3.2] | 46.4 [46.0, 46.8] | 5.7 [5.1, 6.2] | 71.1 [70.7, 71.5] | 7.7 [7.1, 8.3] | 47.7 [45.7, 49.8] | |||
| Chris | Mo/Mo, 27 kV, 50 mAs | Mo/Mo | 23 | 36 | 23.1 [23.0, 23.1] | 68.1 [68.1, 68.1] | 10.9 [10.6, 11.1] | 60.2 [60.1, 60.5] | 23.2 [22.7, 23.8] | 84.0 [83.9, 84.2] | 11.6 [10.0, 13.3] | 59.0 [56.0, 61.9] |
| 25 | 63 | 10.2 [10.1, 10.2] | 12.7 [12.7, 12.7] | 4.2 [4.1, 4.3] | 11.4 [11.3, 11.4] | 8.6 [8.3, 8.9] | 21.4 [21.3, 21.5] | 5.6 [5.3, 5.9] | 14.7 [14.0, 15.5] | |||
| Mo/Mo, 27 kV, 100 mAs | 29 | 45 | 3.8 [3.7, 3.8] | 35.5 [35.5, 35.5] | 1.7 [1.6, 1.8] | 34.7 [34.7, 34.8] | 3.4 [3.3, 3.6] | 57.4 [57.3, 57.4] | 1.4 [1.3, 1.6] | 40.8 [38.9, 42.6] | ||
| 31 | 36 | 6.5 [6.4, 6.5] | 29.1 [29.1, 29.1] | 1.6 [1.5, 1.7] | 29.5 [29.4, 29.6] | 3.2 [3.0, 3.3] | 50.2 [50.1, 50.3] | 2.4 [2.0, 2.8] | 33.5 [31.7, 35.3] | |||
| Diana | Rh/Rh, 29 kV, 63 mAs | Rh/Rh | 25 | 80 | 27.4 [27.4, 27.5] | 70.5 [70.5, 70.5] | 10.0 [9.7, 10.2] | 56.6 [56.4, 56.9] | 21.2 [20.7, 21.8] | 80.9 [80.7, 81.1] | 11.5 [9.4, 13.5] | 56.7 [53.9, 59.5] |
| 27 | 70 | 10.0 [10.0, 10.0] | 21.1 [21.1, 21.1] | 3.8 [3.6, 3.9] | 17.6 [17.5, 17.7] | 7.7 [7.4, 8.0] | 32.1 [31.9, 32.3] | 3.2 [2.8, 3.7] | 20.8 [19.5, 22.0] | |||
| Rh/Rh, 29 kV, 125 mAs | 31 | 56 | 3.2 [3.2, 3.2] | 36.9 [36.9, 36.9] | 2.6 [2.5, 2.7] | 33.9 [33.8, 34.0] | 5.1 [4.9, 5.3] | 56.3 [56.1, 56.4] | 2.3 [2.0, 2.5] | 35.5 [33.5, 37.5] | ||
| 33 | 25 | 5.1 [5.1, 5.1] | 61.7 [61.7, 61.7] | 3.7 [3.6, 3.8] | 56.2 [56.0, 56.3] | 7.1 [6.9, 7.4] | 80.6 [80.5, 80.8] | 6.0 [5.6, 6.3] | 56.3 [53.9, 58.7] | |||
| Elizabeth | Rh/Rh, 30 kV, 110 mAs | Rh/Rh | 26 | 70 | 22.3 [22.2, 22.5] | 68.7 [68.7, 68.7] | 12.0 [11.7, 12.2] | 63.9 [63.7, 64.1] | 25.6 [25.1, 26.2] | 86.8 [86.6, 87.0] | 8.8 [7.5, 10.1] | 58.6 [55.9, 61.3] |
| 28 | 125 | 10.3 [10.2, 10.4] | 17.6 [17.6, 17.6] | 5.8 [5.7, 5.9] | 16.5 [16.5, 16.6] | 12.0 [11.8, 12.3] | 30.3 [30.2, 30.4] | 5.3 [4.8, 5.8] | 17.9 [16.8, 19.0] | |||
| Rh/Rh, 30 kV, 225 mAs | 32 | 100 | 1.2 [1.2, 1.2] | 37.2 [37.2, 37.3] | 1.3 [1.3, 1.4] | 37.2 [37.1, 37.3] | 2.7 [2.5, 2.8] | 60.5 [60.4, 60.7] | 1.7 [1.4, 2.0] | 39.6 [37.7, 41.5] | ||
| 34 | 45 | 2.3 [2.3, 2.4] | 61.5 [61.5, 61.6] | 1.7 [1.6, 1.8] | 60.9 [60.8, 61.1] | 3.4 [3.2, 3.5] | 84.6 [84.5, 84.8] | 2.5 [2.1, 2.8] | 61.1 [58.9, 63.3] | |||
Table 4.
Relative percent error of the local mean signal, local SD, local variance, and PS calculated between target and simulated images, and between original and simulated images, for the condition of lower tube current–time product simulation corresponding to each breast phantom for the GE system.
| Breast phantom | Original techniques factors | Anode/Filter | kV | mAs | Relative error (%) [95% CI] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean signal | SD | Variance | PS | |||||||||
| Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | |||||
| Anna | Mo/Mo, 26 kV, 45 mAs | Mo/Mo | 26 | 22.5 | 1.4 [1.4, 1.4] | 50. [50.0, 50.0] | 3.5 [3.3, 3.7] | 44.1 [43.7, 44.4] | 7.2 [6.6, 7.7] | 68.6 [68.2, 69.0] | 4.4 [3.9, 4.9] | 39.7 [36.9, 42.4] |
| 11 | 1.3 [1.3, 1.3] | 75.6 [75.6, 75.6] | 3.8 [3.5, 4.0] | 64.1 [63.6, 64.6] | 7.6 [7.1, 8.2] | 86.9 [86.5, 87.2] | 4.9 [4.2, 5.6] | 54.0 [50.7, 57.3] | ||||
| Mo/Mo, 22 kV, 140 mAs | 22 | 70 | 2.0 [2.0, 2.1] | 50.7 [50.7, 50.7] | 5.4 [5.1, 5.6] | 48.2 [47.9, 48.6] | 10.3 [9.8, 10.8] | 73.1 [72.7, 73.5] | 5.8 [5.1, 6.5] | 39.8 [36.7, 42.9] | ||
| Mo/Mo, 30 kV, 56 mAs | 30 | 28 | 4.0 [4.0, 4.1] | 50.0 [50.0, 50.0] | 1.9 [1.7, 2.0] | 47.6 [47.5, 47.8] | 3.7 [3.4, 4.0] | 72.5 [72.4, 72.7] | 3.5 [3.0, 4.1] | 49.5 [47.5, 51.6] | ||
| Barbara | Rh/Rh, 29 kV, 45 mAs | Rh/Rh | 29 | 22.5 | 1.0 [0.99, 1.1] | 50.0 [50.0, 50.0] | 2.6 [2.3, 2.8] | 43.9 [43.4, 44.5] | 5.1 [4.7, 5.7] | 68.3 [67.7, 69.0] | 4.0 [3.4, 4.6] | 41.9 [39.5, 44.3] |
| 11 | 0.88 [0.84, 0.92] | 75.6 [75.6, 75.6] | 2.7 [2.4, 2.9] | 65.1 [64.2, 66.1] | 5.3 [4.9, 5.8] | 87.2 [86.5, 88.0] | 5.0 [4.3, 5.7] | 60.0 [57.2, 62.7] | ||||
| Rh/Rh, 25 kV, 160 mAs | 25 | 80 | 0.53 [0.50, 0.57] | 50. [50.0, 50.0] | 2.5 [2.2, 2.7] | 46.1 [45.7, 46.5] | 4.9 [4.4, 5.4] | 70.8 [70.4, 71.3] | 6.4 [5.7, 7.1] | 45.7 [43.4, 48.0] | ||
| Rh/Rh, 33 kV, 50 mAs | 33 | 25 | 0.13 [0.12, 0.14] | 50.0 [50.0, 50.0] | 1.7 [1.5, 1.9] | 46.9 [46.5, 47.3] | 3.4 [3.0, 3.7] | 71.7 [71.3, 72.1] | 4.2 [3.6, 4.9] | 49.9 [48.0, 51.7] | ||
| Chris | Mo/Mo, 27 kV, 50 mAs | Mo/Mo | 27 | 25 | 1.4 [1.4, 1.4] | 50.0 [50.0, 50.0] | 3.1 [2.9, 3.2] | 44.5 [44.4, 44.7] | 6.2 [6.0, 6.4] | 69.1 [69.0, 69.3] | 3.5 [3.3, 3.8] | 45.2 [42.5, 47.8] |
| 12.5 | 1.3 [1.2, 1.3] | 75.0 [75.0, 75.0] | 3.5 [3.3, 3.6] | 66.0 [65.8, 66.2] | 7.1 [6.8, 7.4] | 88.2 [88.1, 88.4] | 3.1 [2.7, 3.5] | 62.3 [59.3, 65.3] | ||||
| Mo/Mo, 23 kV, 70 mAs | 23 | 36 | 1.1 [1.0, 1.1] | 49.3 [49.3, 49.3] | 2.8 [2.7, 2.9] | 39.0 [38.7, 39.3] | 5.6 [5.4, 5.9] | 62.5 [62.2, 62.9] | 1.9 [1.6, 2.1] | 35.5 [32.5, 38.6] | ||
| Mo/Mo, 31 kV, 70 mAs | 31 | 36 | 0.18 [0.18, 0.18] | 49.3 [49.3, 49.3] | 1.6 [1.5, 1.6] | 47.5 [47.4, 47.6] | 3.2 [3.0, 3.3] | 72.4 [72.3, 72.5] | 2.6 [2.3, 2.9] | 57.4 [55.8, 59.0] | ||
| Diana | Rh/Rh, 29 kV, 63 mAs | Rh/Rh | 29 | 32 | 0.92 [0.92, 0.93] | 49.2 [49.2, 49.2] | 3.0 [2.9, 3.1] | 40.0 [39.8, 40.3] | 6.1 [5.8, 6.3] | 63.8 [63.6, 64.1] | 2.4 [2.2, 2.6] | 40.5 [38.0, 43.0] |
| 16 | 0.29 [0.28, 0.29] | 74.6 [74.6, 74.6] | 2.7 [2.6, 2.8] | 59.5 [59.2, 59.8] | 5.4 [5.2, 5.6] | 83.2 [83.0, 83.5] | 2.1 [1.8, 2.4] | 58.6 [55.7, 61.4] | ||||
| Rh/Rh, 25 kV, 160 mAs | 25 | 80 | 1.1 [1.1, 1.1] | 50.0 [49.9, 50.0] | 3.5 [3.4, 3.7] | 31.1 [30.8, 31.4] | 7.1 [6.8, 7.3] | 52.2 [51.8, 52.6] | 2.0 [1.7, 2.3] | 31.0 [28.1, 33.8] | ||
| Rh/Rh, 33 kV, 50 mAs | 33 | 25 | 0.33 [0.33, 0.34] | 50.0 [50.0, 50.0] | 2.6 [2.5, 2.6] | 43.5 [43.3, 43.7] | 5.1 [4.9, 5.2] | 68.0 [67.8, 68.1] | 1.8 [1.6, 2.0] | 46.2 [44.0, 48.3] | ||
| Elizabeth | Rh/Rh, 30 kV, 110 mAs | Rh/Rh | 30 | 56 | 0.49 [0.47, 0.52] | 49.1 [49.1, 49.1] | 2.1 [2.0, 2.2] | 45.8 [45.6, 46.0] | 4.2 [4.0, 4.4] | 70.5 [70.3, 70.7] | 1.6 [1.4, 1.7] | 42.5 [40.0, 45.1] |
| 28 | 0.40 [0.39, 0.42] | 74.5 [74.5, 74.6] | 2.6 [2.5, 2.7] | 69.0 [68.7, 69.2] | 5.3 [5.0, 5.5] | 90.1 [89.9, 90.3] | 3.1 [2.8, 3.4] | 61.3 [58.5, 64.1] | ||||
| Rh/Rh, 26 kV, 140 mAs | 26 | 70 | 1.5 [1.5, 1.6] | 50.0 [50.0, 50.0] | 2.8 [2.7, 2.9] | 43.6 [43.3, 43.9] | 5.6 [5.4, 5.8] | 67.8 [67.5, 68.2] | 1.7 [1.5, 2.0] | 36.8 [33.9, 39.7] | ||
| Rh/Rh, 34 kV, 90 mAs | 34 | 45 | 0.12 [0.11, 0.12] | 50.0 [50.0, 50.0] | 1.5 [1.5, 1.6] | 47.8 [47.7, 48.0] | 3.1 [2.9, 3.2] | 72.7 [72.6, 72.9] | 1.6 [1.4, 1.9] | 48.9 [46.8, 51.0] | ||
Table 5.
Relative percent error of the local mean signal, local SD, local variance, and PS calculated between target and simulated images, and between original and simulated images, for the condition of lower and higher tube voltage simulation corresponding to each breast phantom for the Hologic system.
| Breast phantom | Original techniques factors | Anode/Filter | kV | mAs | Relative error (%) [95% CI] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Variance | PS | |||||||||
| Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | |||||
| Anna | W/Rh, 26 kV, 70 mAs | W/Rh | 22 | 120 | 28.4 [28.4, 28.5] | 39.1 [39.0, 39.1] | 14.9 [14.6, 15.1] | 28.5 [28.4, 28.7] | 32.1 [31.5, 32.7] | 48.9 [48.7, 49.1] | 24.7 [23.3, 26.2] | 43.0 [42.1, 43.8] |
| W/Rh, 26 kV, 140 mAs | 28 | 50 | 1.2 [1.2, 1.2] | 51.7 [51.7, 51.7] | 1.9 [1.8, 2.0] | 43.0 [42.7, 43.3] | 3.9 [3.7, 4.1] | 67.4 [67.1, 67.7] | 3.6 [3.2, 4.1] | 52.8 [51.2, 54.4] | ||
| 30 | 35 | 0.76 [0.74, 0.78] | 56.2 [56.2, 56.2] | 2.0 [1.9, 2.1] | 47.1 [46.8, 47.4] | 4.0 [3.8, 4.2] | 71.8 [71.5, 72.1] | 2.3 [2.0, 2.6] | 57.1 [55.5, 58.7] | |||
| Barbara | W/Rh, 28 kV, 110 mAs | W/Rh | 24 | 120 | 5.4 [5.3, 5.4] | 46.5 [46.5, 46.5] | 3.8 [3.6, 4.0] | 36.2 [35.8, 36.7] | 7.9 [7.5, 8.3] | 59.1 [58.6, 59.6] | 6.3 [5.8, 6.9] | 48.3 [47.0, 49.5] |
| W/Rh, 28 kV, 220 mAs | 30 | 80 | 1.8 [1.7, 1.8] | 52.7 [52.6, 52.7] | 2.8 [2.6, 2.9] | 44.4 [43.9, 45.0] | 5.7 [5.3, 6.0] | 68.8 [68.2, 69.3] | 7.7 [7.1, 8.4] | 53.7 [52.3, 55.2] | ||
| 32 | 65 | 4.2 [4.1, 4.3] | 50.5 [50.5, 50.5] | 2.7 [2.6, 2.9] | 42.6 [42.0, 43.1] | 5.6 [5.2, 5.9] | 66.6 [65.9, 67.2] | 7.4 [6.7, 8.1] | 50.6 [49.0, 52.2] | |||
| W/Ag | 30 | 50 | 4.8 [4.7, 4.9] | 46.2 [46.1, 46.2] | 8.5 [8.2, 8.8] | 40.0 [39.4, 40.6] | 17.9 [17.3, 18.4] | 63.5 [62.8, 64.2] | 13.5 [12.6, 14.4] | 48.2 [46.6, 49.8] | ||
| 32 | 40 | 19.9 [19.7, 20.0] | 56.9 [56.9, 57.0] | 10.0 [9.8, 10.2] | 48.7 [48.1, 49.4] | 18.9 [18.5, 19.3] | 73.1 [72.4, 73.8] | 13.3 [12.5, 14.2] | 57.7 [56.1, 59.3] | |||
| Chris | W/Rh, 27 kV, 85 mAs | W/Rh | 23 | 110 | 16.0 [16.0, 16.1] | 45.1 [45.1, 45.1] | 10.3 [10.2, 10.4] | 34.6 [34.5, 34.7] | 21.8 [21.5, 22.1] | 57.2 [57.0, 57.3] | 18.1 [17.5, 18.7] | 50.8 [49.9, 51.6] |
| W/Rh, 27 kV, 170 mAs | 29 | 60 | 1.8 [1.7, 1.8] | 53.2 [53.2, 53.2] | 2.4 [2.3, 2.4] | 45.8 [45.7, 45.9] | 4.8 [4.6, 4.9] | 70.5 [70.3, 70.6] | 2.2 [1.9, 2.5] | 58.8 [57.6, 60.0] | ||
| 31 | 50 | 1.4 [1.4, 1.5] | 49.8 [49.8, 49.8] | 2.3 [2.2, 2.4] | 43.5 [43.4, 43.7] | 4.6 [4.5, 4.8] | 68.0 [67.8, 68.1] | 3.6 [3.1, 4.1] | 56.1 [54.9, 57.3] | |||
| Diana | W/Rh, 29 kV, 120 mAs | W/Rh | 25 | 140 | 4.0 [4.0, 4.0] | 38.0 [38.0, 38.0] | 2.5 [2.4, 2.5] | 27.7 [27.6, 27.8] | 5.0 [4.9, 5.2] | 47.6 [47.5, 47.7] | 3.2 [2.9, 3.5] | 41.7 [40.6, 42.8] |
| 27 | 140 | 0.10 [0.09, 0.10] | 13.1 [13.1, 13.1] | 2.3 [2.3, 2.4] | 9.5 [9.5, 9.6] | 4.7 [4.6, 4.9] | 18.1 [18.0, 18.2] | 3.4 [3.2, 3.7] | 15.8 [15.3, 16.2] | |||
| W/Rh, 29 kV, 240 mAs | 31 | 95 | 4.8 [4.7, 4.8] | 49.5 [49.5, 49.5] | 2.1 [2.0, 2.1] | 37.7 [37.5, 37.8] | 4.2 [4.1, 4.3] | 61.0 [60.8, 61.2] | 4.1 [3.8, 4.5] | 48.2 [46.4, 49.9] | ||
| 33 | 70 | 9.3 [9.3, 9.3] | 52.3 [52.3, 52.3] | 2.2 [2.2, 2.3] | 38.8 [38.6, 38.9] | 4.4 [4.3, 4.5] | 62.3 [62.1, 62.5] | 3.1 [2.8, 3.4] | 47.8 [45.8, 49.8] | |||
| W/Ag | 33 | 42.5 | 2.1 [2.1, 2.1] | 59.0 [59.0, 59.0] | 9.3 [9.2, 9.4] | 44.8 [44.7, 45.0] | 17.7 [17.5, 17.8] | 69.2 [69.1, 69.4] | 14.8 [13.9, 15.8] | 55.2 [53.2, 57.1] | ||
| Elizabeth | W/Ag, 30 kV, 150 mAs | W/Ag | 26 | 80 | 11.1 [11.0, 11.1] | 72.9 [72.9, 72.9] | 12.2 [12.1, 12.4] | 60.3 [60.0, 60.5] | 26.2 [25.9, 26.5] | 83.8 [83.6, 84.0] | 32.3 [28.8, 35.7] | 68.7 [66.9, 70.5] |
| 28 | 180 | 3.6 [3.6, 3.6] | 12.2 [12.2, 12.2] | 3.3 [3.2, 3.3] | 9.6 [9.5, 9.6] | 6.7 [6.5, 6.9] | 18.2 [18.1, 18.2] | 11.1 [9.8, 12.4] | 12.9 [12.2, 13.6] | |||
| W/Ag, 30 kV, 300 mAs | 32 | 120 | 0.76 [0.74, 0.77] | 47.8 [47.8, 47.8] | 3.1 [3.0, 3.1] | 43.2 [43.1, 43.4] | 6.3 [6.1, 6.4] | 67.6 [67.4, 67.8] | 10.2 [9.5, 10.9] | 51.1 [49.5, 52.7] | ||
| 34 | 85 | 2.1 [2.0, 2.1] | 51.5 [51.4, 51.5] | 5.6 [5.5, 5.7] | 46.6 [46.4, 46.8] | 11.5 [11.3, 11.7] | 71.2 [71.0, 71.5] | 14.3 [13.6, 14.9] | 53.1 [51.3, 54.9] | |||
Table 6.
Relative percent error of the local mean signal, local SD, local variance, and PS calculated between target and simulated images, and between original and simulated images, for the condition of lower tube current–time product simulation corresponding to each breast phantom for the Hologic system.
| Breast phantom | Original techniques factors | Anode/Filter | kV | mAs | Relative error (%) [95% CI] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Variance | PS | |||||||||
| Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | Sim/Targ | Sim/Orig | |||||
| Anna | W/Rh, 26 kV, 70 mAs | W/Rh | 26 | 35 | 0.89 [0.88, 0.90] | 50.3 [50.3, 50.3] | 2.4 [2.3, 2.5] | 36.2 [35.9, 36.5] | 4.8 [4.5, 5.0] | 59.2 [58.8, 59.5] | 4.5 [4.1, 4.9] | 47.8 [46.2, 49.3] |
| 18 | 3.0 [3.0, 3.0] | 74.5 [74.5, 74.5] | 2.8 [2.6, 2.9] | 54.8 [54.4, 55.1] | 5.6 [5.3, 5.9] | 79.3 [78.9, 79.6] | 5.2 [4.7, 5.7] | 69.0 [67.6, 70.5] | ||||
| W/Rh, 22 kV, 240 mAs | 22 | 120 | 1.1 [1.1, 1.1] | 50.3 [50.3, 50.3] | 2.0 [1.9, 2.1] | 38.0 [37.7, 38.3] | 4.0 [3.8, 4.2] | 61.4 [61.0, 61.7] | 3.0 [2.6, 3.5] | 48.0 [46.4, 49.7] | ||
| W/Rh, 30 kV, 70 mAs | 30 | 35 | 0.08 [0.07, 0.08] | 50.3 [50.3, 50.3] | 2.0 [1.9, 2.1] | 39.8 [39.5, 40.0] | 4.1 [3.8, 4.3] | 63.5 [63.2, 63.9] | 3.4 [3.0, 3.7] | 50.4 [48.9, 52.0] | ||
| Barbara | W/Rh, 28 kV, 110 mAs | W/Rh | 28 | 55 | 0.69 [0.68, 0.70] | 50.1 [50.1, 50.1] | 2.4 [2.2, 2.6] | 37.6 [37.0, 38.2] | 4.9 [4.5, 5.2] | 60.6 [59.9, 61.4] | 6.0 [5.4, 6.6] | 47.1 [45.6, 48.6] |
| 28 | 0.55 [0.52, 0.58] | 74.6 [74.6, 74.6] | 3.6 [3.4, 3.8] | 57.3 [56.5, 58.0] | 7.3 [6.8, 7.8] | 80.9 [80.3, 81.6] | 7.7 [6.9, 8.5] | 69.0 [67.6, 70.4] | ||||
| W/Rh, 24 kV, 240 mAs | 24 | 120 | 0.13 [0.12, 0.14] | 50.2 [50.2, 50.2] | 2.1 [2.0, 2.3] | 38.4 [37.8, 39.0] | 4.3 [4.0, 4.6] | 61.6 [60.8, 62.3] | 4.2 [3.8, 4.7] | 47.4 [45.9, 49.0] | ||
| W/Rh, 32 kV, 130 mAs | 32 | 65 | 0.98 [0.97, 0.98] | 50.2 [50.2, 50.2] | 2.2 [2.0, 2.3] | 41.0 [40.5, 41.5] | 4.4 [4.0, 4.7] | 64.9 [64.2, 65.4] | 5.9 [5.3, 6.6] | 49.9 [48.4, 51.4] | ||
| W/Ag, 32 kV, 80 mAs | W/Ag | 32 | 40 | 0.47 [0.46, 0.48] | 50.2 [50.2, 50.2] | 1.9 [1.8, 2.1] | 40.7 [40.2, 41.2] | 3.9 [3.6, 4.2] | 64.5 [63.9, 65.1] | 5.5 [4.9, 6.1] | 51.4 [50.0, 52.8] | |
| Chris | W/Rh, 27 kV, 85 mAs | W/Rh | 27 | 42.5 | 5.4 [5.3, 5.4] | 50.3 [50.3, 50.3] | 2.7 [2.6, 2.8] | 38.5 [38.2, 38.6] | 5.5 [5.3, 5.6] | 62.0 [61.8, 62.2] | 2.3 [2.0, 2.5] | 52.7 [51.5, 53.9] |
| 22 | 6.8 [6.7, 6.8] | 74.3 [74.3, 74.3] | 3.4 [3.3, 3.5] | 57.5 [57.2, 57.7] | 6.9 [6.7, 7.1] | 81.6 [81.5, 81.8] | 2.1 [1.9, 2.3] | 73.2 [72.1, 74.3] | ||||
| W/Rh. 23 kV, 220 mAs | 23 | 110 | 0.54 [0.53, 0.56] | 50.3 [50.3, 50.3] | 1.9 [1.9, 2.0] | 39.5 [39.4, 39.7] | 3.8 [3.7, 3.9] | 63.3 [63.1, 63.4] | 1.5 [1.2, 1.8] | 52.2 [50.9, 53.5] | ||
| W/Rh, 31 kV, 100 mAs | 31 | 50 | 0.12 [0.12, 0.12] | 50.4 [50.4, 50.4] | 1.8 [1.7, 1.8] | 42.0 [41.9, 42.2] | 3.6 [3.5, 3.7] | 66.3 [66.1, 66.4] | 2.2 [1.8, 2.6] | 54.9 [53.7, 56.1] | ||
| Diana | W/Rh, 29 kV, 120 mAs | W/Rh | 29 | 60 | 0.35 [0.34, 0.35] | 50.7 [50.7, 50.7] | 2.6 [2.5, 2.7] | 33.4 [33.2, 33.5] | 5.3 [5.1, 5.4] | 55.4 [55.2, 55.6] | 5.3 [4.8, 5.9] | 46.4 [44.7, 48.0 |
| 30 | 0.35 [0.34, 0.36] | 75.3 [75.3, 75.3] | 2.5 [2.4, 2.6] | 52.7 [52.5, 52.8] | 5.0 [4.9, 5.2] | 77.3 [77.2, 77.5] | 4.0 [3.6, 4.4] | 69.5 [68.1, 71.0] | ||||
| W/Rh, 25 kV, 280 mAs | 25 | 140 | 1.3 [1.3, 1.3] | 50.4 [50.4, 50.4] | 2.5 [2.4, 2.5] | 35.9 [35.7, 36.0] | 5.0 [4.9, 5.1] | 58.7 [58.5, 58.9] | 4.0 [3.6, 4.3] | 47.9 [46.2, 49.6] | ||
| W/Rh, 33 kV, 140 mAs | 33 | 70 | 0.59 [0.59, 0, 60] | 50.3 [50.3, 50.3] | 2.8 [2.7, 2.9] | 37.1 [36.9, 37.2] | 5.7 [5.5, 5.8] | 60.2 [60.0, 60.4] | 6.8 [6.2, 7.4] | 49.6 [47.9, 51.2] | ||
| W/Ag, 33 kV, 80 mAs | W/Ag | 33 | 42.5 | 0.11 [0.11, 0.11] | 47.2 [47.2, 47.2] | 2.7 [2.7, 2.8] | 34.0 [33.8, 34.1] | 5.6 [5.5, 5.7] | 56.2 [56.1, 56.4] | 7.1 [6.5, 7.8] | 46.5 [44.9, 48.1] | |
| Elizabeth | W/Ag, 30 kV, 150 mAs | W/Ag | 30 | 75 | 0.58 [0.56, 0.59] | 50.8 [50.8, 50.8] | 2.3 [2.2, 2.3] | 42.2 [42.0, 42.4] | 4.6 [4.5, 4.7] | 66.3 [66.1, 66.6] | 6.9 [6.2, 7.5] | 51.1 [49.6, 52.7] |
| 37.5 | 1.6 [1.6, 1.6] | 75.4 [75.4, 75.4] | 2.9 [2.8, 3.0] | 63.1 [62.8, 63.3] | 5.9 [5.7, 6.1] | 85.9 [85.7, 86.1] | 6.5 [5.8, 7.1] | 72.9 [71.5, 74.3] | ||||
| W/Ag, 26 kV, 160 mAs | 26 | 80 | 3.6 [3.6, 3.7] | 50.6 [50.6, 50.6] | 3.1 [3.0, 3.1] | 36.3 [36.0, 36.6] | 6.2 [6.1, 6.4] | 58.9 [58.6, 59.3] | 12.4 [10.7, 14.0] | 41.1 [38.8, 43.3] | ||
| W/Ag, 34 kV, 170 mAs | 34 | 85 | 0.56 [0.55, 0.56] | 50.5 [50.5, 50.5] | 1.9 [1.8, 2.0] | 44.1 [43.9, 44.2] | 3.8 [3.7, 4.0] | 68.6 [68.4, 68.7] | 7.7 [7.0, 8.4] | 51.9 [50.2, 53.5] | ||
Fig. 5.
(a) Power spectrum of the original, target, and simulated images of the 3D-printed breast phantom, Diana for the GE system; (b) correlation between target and simulated images: and . For correlation between original and simulated images: [0.619, 0.621; 0.104, 0.112] and ; (c) target-simulated image subtraction; (d) original-simulated image subtraction. Target and simulated image: Rh/Rh 27 kV, 70 mAs, original image: Rh/Rh 29 kV, 63 mAs.
Fig. 6.
(a) Power spectrum of the original, target, and simulated images of the 3D-printed breast phantom, Diana for the GE system; (b) correlation between target and simulated images: and . For correlation between original and simulated images: [0.389, 0.390; 0.271, 0.284] and ; (c) target-simulated image subtraction; (d) original-simulated image subtraction. Target and simulated images: Rh/Rh 31 kV, 56 mAs, original image: Rh/Rh 29 kV, 125 mAs.
Fig. 7.
(a) Power spectrum of the original, target, and simulated images of the 3D-printed breast phantom, Diana for the GE system; (b) correlation between target and simulated images: and . For correlation between original and simulated images: [0.062, 0.064; 0.190, 0.193] and ; (c) target-simulated image subtraction; (d) original-simulated image subtraction. Target and simulated images: Rh/Rh 29 kV, 16 mAs, original image: Rh/Rh 29 kV, 63 mAs.
Fig. 8.
(a) Power spectrum of the original, target, and simulated images of the 3D-printed breast phantom, Diana for the Hologic system; (b) correlation between target and simulated images: [1.008, 1.019; 0.015, 0.044] and . For correlation between original and simulated images: [0.395, 0.398; 0.563, 0.576] and ; (c) target-simulated image subtraction; (d) original-simulated image subtraction. Target and simulated images: W/Rh 25 kV, 140 mAs, original image: W/Rh 29 kV, 120 mAs. The peak observed at frequency resulted from an anti-scatter grid artifact.
Fig. 9.
(a) Power spectrum of the original, target, and simulated images of the 3D-printed breast phantom, Diana for the Hologic system; (b) correlation between target and simulated images: [0.727, 0.735; 0.397, 0.439] and . For correlation between original and simulated images: [0.152, 0.153; 1.814, 1.832] and ; (c) target-simulated image subtraction; (d) original-simulated image subtraction. Target and simulated images: W/Ag 33 kV, 42.5 mAs, original image: W/Rh 29 kV, 240 mAs. The peak observed at frequency resulted from an anti-scatter grid artifact.
Fig. 10.
(a) Power spectrum of the original, target, and simulated images of the 3D-printed breast phantom, Diana for the Hologic system; (b) correlation between target and simulated images: [0.973, 0.987; 0.097, 0.126] and . For correlation between original and simulated images: [0.245, 0.248; 0.882, 0.895] and ; (c) target-simulated image subtraction; (d) original-simulated image subtraction. Target and simulated images: W/Rh 29 kV, 60 mAs, original image: W/Rh 29 kV, 120 mAs. The peak observed at frequency resulted from an anti-scatter grid artifact.
Residual images for one set of lower and higher tube voltage simulations and one lower tube current–time product simulation are also shown in Figs. 5–7 for GE and in Figs. 8–10 for Hologic. In the subtraction between target and simulated images, mostly random noise remains, which shows the similarity between the images. In the subtraction between original and simulated images, structures remain since the images are different. However, in Fig. 9, some remaining structures are also observed, which shows lower similarity between the target and simulated images than observed in the other cases, as also seen in the corresponding PS.
4. Discussion
An algorithm to simulate images with different technique factors (higher or lower tube voltages, different anode/filter combinations, or lower tube current–time products) resulting in changes in contrast and/or noise was validated using five patient-based 3D-printed breast phantoms of different thicknesses and compositions acquired at those conditions for each of the two systems.
Overall, the image quality modification algorithm worked accurately in simulating images acquired with different technique factors. Specifically, the algorithm worked more accurately when simulating images acquired with a lower tube current–time product than when simulating images acquired with different tube voltages or anode/filter combinations (Tables 3 and 4 for the GE system and Tables 5 and 6 for the Hologic systems). This may be because this type of simulation requires fewer measurements for input of parameters, factors, and conditions than the other modifications.24,25,28 Moreover, the algorithm was not so accurate in simulating images acquired with a lower tube voltage or with a different anode/filter combination with the Hologic system as it was with the other system in terms of noise simulation, resulting in higher relative percent error values of PS. This may be related to the selected technique factors that resulted in high-noise target images, which make the comparison between the simulated and target images also noisy.
Importantly, on average, there were no substantial variations in the relative percent error between the local mean signal, local SD, local variance, and PS of the target and simulated images among the five phantoms. Even the lower accuracy of the algorithm on simulating images as if acquired with different tube voltages, previously mentioned, was consistent across phantoms. Only when simulating Elizabeth images acquired with Hologic, the algorithm worked less accurately, specifically when simulating images as if acquired with a lower tube current–time product. That is because Elizabeth replicates a very dense breast, resulting in these images being formed with a very low signal, as previously mentioned. This leads to too high-noise images and therefore a noisy comparison. This means that, therefore, the performance of the algorithm to simulate images acquired with different technique factors was not affected using phantoms that replicate equivalent breasts of different densities and thicknesses.
In this study, anthropomorphic 3D-printed phantoms simulating real mammograms of breasts with different thicknesses and compositions were used. In this way, it was possible to replicate conditions that are found in the clinical setting, which are not possible to obtain with homogeneous slabs. However, similar to the homogeneous slabs, the breast phantoms are also composed of a single material, whereas the breast is composed of several different tissue types with different characteristics and attenuations. Nevertheless, the differences between breast tissues are included in the development of these phantoms since they are developed directly from real mammograms. Moreover, in the validation of the phantom model, the anatomical structures and associated attenuation characteristics of the breast phantom and real mammograms matched for the specific factors used to acquire the corresponding mammogram.37
This validation study has some limitations. The scatter was assumed to be uniform over the image, which is not a valid assumption near the breast edge. Therefore, the accuracy of the modification algorithm close to the skin line is not verified. In addition, this is the region where the phantoms do not match the real mammogram completely.37 As a consequence, the validations were performed using selected and centered ROIs instead of the whole image. However, this area might not have a high clinical impact since only a few cancer cases are found there.39 Finally, it is important to state that each of the breast phantoms already contains the physical characteristics of the real mammograms from which the phantoms were developed. However, the phantom developers determined that the phantoms can be used in systems from different manufactures and of different designs, given the slight differences in system geometry and acquisition factors across mammographic systems.37 Moreover, the phantoms were used for comparisons between phantom images. Therefore, the exact correspondence between each phantom and its corresponding real mammogram is not necessary because only phantom images were used for this validation study. This is further shown by the fact that the phantoms were based on mammograms acquired with two different systems and were used here on two other systems. Therefore, any issue related to the design of the phantom applies to both the target and simulated images and hence should not have affected the validation results.
In the future, this algorithm will be applied to clinical images to evaluate the effect of changing technique factors on cancer detection. This will also be important for understanding and improving the performance of clinical evaluation and observer studies. This study was the first step to mathematically test and validate this image modification algorithm on “for processing” images only, to be used in future research on evaluating image quality in real patient images. For future work, it is of interest to validate this modification algorithm by comparing the processed versions of the images to understand if any small deviations in the “for processing” modified images could result in large deviations in the “for presentation” ones.
5. Conclusions
An algorithm to simulate images acquired at different technique factors resulting in changes of contrast or noise was evaluated and was found to work accurately on patient-based 3D-printed breast phantoms of different thicknesses and compositions. This tool can be used in studies to evaluate the impact of changing technique characteristics in image quality and in cancer detection using clinical images.
6. Appendix: Mammography Systems Characterization and Phantom Specifications
The Senographe Essential (GE Healthcare, Buc, France) and the Lorad Selenia (Hologic, Inc., Bedford, Massachusetts) digital mammography systems were characterized in terms of first HVL, STP, grid factor, NPS to calculate the noise model, glare and scatter properties, and flat-field correction, to be able to apply the algorithm that simulates images as if they were acquired with different technique factors. The standard technique factors were selected by the AEC of both systems for a range of thicknesses of PMMA slabs (20 to 80 mm for GE, and 10 to 80 mm for Hologic). The reference beam quality selected by the AEC for a 45-mm-thick PMMA slab was 29-kV Rh anode and 0.025-mm-thick Rh filter for GE and 30-kV W anode and 0.050-mm-thick Rh filter for Hologic.
6.1. Half Value Layer
The tube output and the first HVL of both systems were measured over a range of technique factors and anode/filter combinations following the standard methodology defined in the IPEM report 89.31 A calibrated Radcal Accu-Pro (Radcal Corp., Monrovia, California) dosimeter with mammography ionization chamber centered 60 mm from the chest wall and 70 mm above the detector for GE and 45 mm above the detector for Hologic was used to measure the air kerma for the selected factors.
6.2. System Transfer Properties and Absorbed Energy per Unit Area per Incident Air Kerma ()
As part of the image modification algorithm, the image needs to be linearized to represent the absorbed energy per unit area. For this, the STP, which consist of the relationship between the PV in the image and , the absorbed energy, were calculated in several steps: (1) the conversion factor , which relates the to the incident air kerma at the detector (DKE), was calculated for the reference beam quality for each system, referred above. (2) Flat-field images of a 45-mm-thick PMMA slab, placed at the tube head, were acquired with the reference beam quality for each system for detector air kerma values varying approximately between 20 and .32 The radiation field was collimated to about , the compression paddle was included and placed as high as possible, and the anti-scatter grid was removed. (3) Keeping the same setup and technique factors, the air kerma was measured with the setup described above for tube output and HVL. (4) The detector air kerma was calculated by correcting the measured air kerma using the inverse square law. (5) The detector air kerma values were then converted to the absorbed energy per unit area by multiplying them by the factor. (6) The PVs were measured within a ROI laterally centered within the measured images and positioned 60 mm from the chest wall. (7) Finally, the STP were calculated as the relationship between the PV and .
The factor was also needed for the estimation of the value of certain parameters in the image modification algorithm.25 Hence, it was also calculated over the range of PMMA thicknesses, mentioned previously. Consequently, it was measured over a range of tube voltages and anode/filter combinations. Specifically, for the 30, 45, and 60 mm thicknesses of PMMA, images were acquired at more variations of technique factors: different anode/filter combinations, lower and higher tube voltages, and lower tube current–exposure time products. For this, the air kerma was again measured using the same setup described previously, and images of the different homogeneous PMMA slab phantoms were acquired to measure the corresponding PV. The absorbed energy per unit area was calculated for each beam quality and thickness of PMMA using the STP. Finally, the factor was calculated using the relationship between and the calculated DKE for each beam quality and thickness of PMMA.
and the fit of the mean PV against absorbed energy per unit area was obtained for the reference beam quality of 45-mm PMMA for each system so that for the GE system at Rh/Rh 29 kV, 45 mm PMMA. Also, DKE – 6.0006 (). For the Hologic system at W/Rh 30 kV, 45 mm PMMA. Also, DKE – 61.158 ().
6.3. Grid Factor
The grid factor can be defined as the ratio of primary x-ray photons transmitted through the anti-scatter grid in a mammography system over the incident ones. It is required as part of the calculation of the signal at the detector position.
To estimate the grid factor, images were acquired at high dose, with the technique factors of interest, for 30-, 45-, and 60-mm-thick PMMA slabs placed at the tube head, to minimize the scatter at the detector. The radiation field was collimated to about , and images were made with and without the grid in the field of view and with the compression paddle included. The grid factor was then calculated using the ratio of the absorbed energy calculated for the image with grid to the one without grid.33 The average of the calculated grid factors of all beam qualities corresponding to each anode/filter combination for each thickness were used.
The grid factor was measured over a range of tube voltages and anode/filter combinations specifically for three thicknesses of PMMA, and there were very small changes observed in the calculated grid factor. Therefore, the grid factor was averaged across anode/filter combinations for each PMMA thickness and the resultant values are shown in Tables 7 and 8 for the GE and Hologic systems, respectively.
Table 7.
Average of the grid factor for each PMMA thickness and anode/filter combination measured for the GE system.
| GE | ||
|---|---|---|
| PMMA (mm) | Mo/Mo | Rh/Rh |
| 30 | 0.64 | — |
| 45 | 0.66 | 0.67 |
| 60 | — | 0.69 |
Table 8.
Average of the grid factor for each PMMA thickness and anode/filter combination measured for the Hologic system.
| Hologic | ||
|---|---|---|
| PMMA (mm) | W/Rh | W/Ag |
| 30 | 0.72 | 0.73 |
| 45 | 0.72 | 0.72 |
| 60 | 0.73 | 0.72 |
6.4. Flat-Field Correction
The flat-field correction allows for measuring the variation of exposure throughout the image due to the heel effect and variations in the magnitude of scatter.
A 40-mm-thick flat clean PMMA slab, placed on the breast support table, was imaged five times with the same technique factors and setup used for the flat-field calibration of the systems and the variance map of the noise across the detector was calculated.34 Since the quantum noise is the dominant noise source, the variance map is proportional to the inverse of the flat-field correction applied to the image. The flat-field correction map was calculated by a two-dimensional fit to the variance map.
6.5. Noise Power Spectra
To obtain the noise model needed for the image modification algorithm, the noise coefficients for the quantum noise, electronic noise, and structure noise were calculated from the measured NPS.
For this, multiple images of 45-mm-thick PMMA slabs, placed on the breast support table, were acquired with the reference spectrum, for a range of detector air kerma from approximately 20 to . The x-ray beam was collimated to approximately ; the anti-scatter grid and the compression paddle (in contact with the PMMA) were in the field of view. The PVs in each image were normalized to using the inverse of the STP described earlier. The NPS was then calculated and normalized for each image in a laterally centered ROI, positioned 60 mm from the chest wall edge. The ROI was split into several half-overlapping sub-ROIs of . The final NPS was estimated for each sub-ROI and averaged for each dose level.35 The three noise coefficients were then estimated by applying a two-dimensional fit to relate to each spatial frequency.
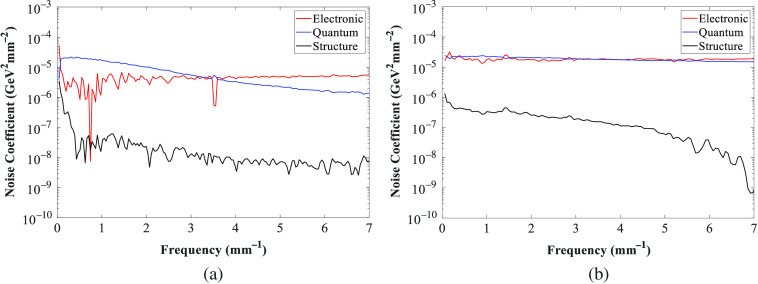
The quantum noise coefficient is beam quality sensitive, that is, it is different for each beam quality compared with the reference beam quality. On the other hand, it is assumed that the structure and electronic noise coefficients are not beam quality sensitive. So the quantum noise coefficient needed to be corrected for each beam quality.25 Keeping the same setup used for the reference noise coefficient measurements, flat-field images over the range of thicknesses of PMMA described earlier were acquired for each system at the dose level set by the AEC. For the 30, 45, and 60 mm thicknesses of PMMA, images were acquired at more variations of technique factors: different anode/filter combinations, lower and higher tube voltages, and lower tube current–exposure time products. The NPS was calculated and normalized for each beam quality. Then, the quantum noise coefficients were also calculated for each beam quality using the information of the reference noise coefficients calculated previously and the measured NPS.
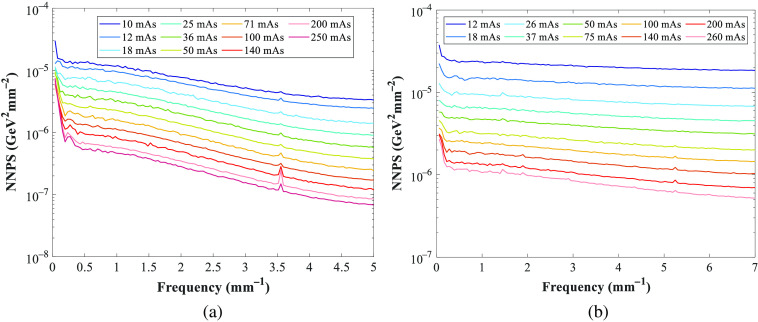
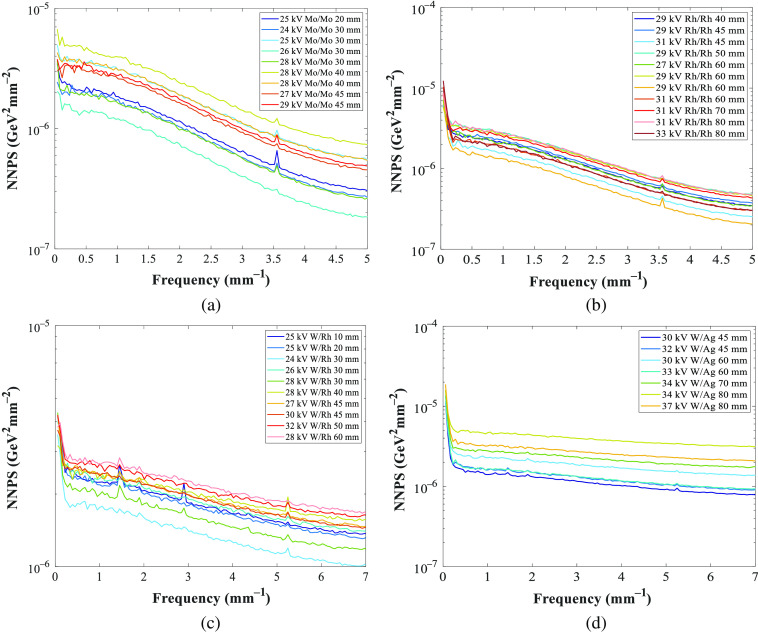
Figure 11 shows the normalized noise power spectra (NNPS) measured for the GE and Hologic systems at the reference beam quality of 45-mm PMMA and used to calculate the noise coefficients (Fig. 12). The NNPS was also calculated over a range of technique factors and for different PMMA thicknesses (Fig. 13) to estimate the quantum noise coefficient.
Fig. 11.
NNSP measured at the reference beam quality of 45-mm PMMA for the (a) GE and (b) Hologic systems. The peaks observed at frequency 3.5 and for GE and Hologic, respectively, are related to an anti-scatter grid artifact.
Fig. 12.
Noise coefficients (electronic, quantum and structure) for (a) GE and (b) Hologic systems. The peak observed at frequency for GE is related to an anti-scatter grid artifact.
Fig. 13.
NNPS calculated for different tube voltages, anode/filter combinations, and PMMA thicknesses, for (a), (b) GE and (c), (d) Hologic systems. The peaks observed at frequency 3.5 and for GE and Hologic, respectively, are related to an anti-scatter grid artifact.
6.6. Glare and Scatter Properties
The GPR was measured with a lead disk phantom with five lead disks of diameter between 1 and 3 mm placed embedded in a 2-mm-thick PMMA on the breast support table, with the AEC beam quality and high tube current–time product, with anti-scatter grid, without compression paddle, and with 2-mm-thick aluminum at the tube head. The SPR was acquired using the same lead disk phantom but placed on the compression paddle that was in contact with the PMMA slabs and for 30, 45, and 60 mm of PMMA.33 The GPR and the SPR were then calculated by comparing the PVs in the background and within the disks in the image. The measured SPR already includes a contribution from the glare, so each value of SPR was corrected by removing the GPR.
The GPR was found to be 0.0857 and 0.0237 for GE and Hologic, respectively. The SPR was measured for the three PMMA thicknesses of interest and different anode/filter combinations for the GE and Hologic systems. For Hologic, the values were calculated previously.28 A relationship between the SPR and kV was found and is shown in Table 9.
Table 9.
Equations for SPR for the GE and Hologic systems.
| PMMA (mm) | Anode/Filter | SPR equation |
|---|---|---|
| GE | ||
| 30 | Mo/Mo | |
| 45 | Rh/Rh | |
| 60 | Mo/Mo | |
| 60 | Rh/Rh | |
| Hologic | ||
| 30 | W/Rh | |
| 45 | W/Rh | |
| 45 | W/Ag | |
| 60 | W/Rh | |
| 60 | W/Ag | |
6.7. Phantom Specifications
The phantoms were developed using anonymized patient mammograms that were acquired at specific conditions. Table 10 shows all of the parameters used to acquire each of the patient mammograms corresponding to each 3D-printed breast phantom.
Table 10.
Parameters used to acquire each patient mammogram corresponding to each 3D-printed breast phantom.
| Breast phantom | DM system | Detector Type | Pixel size (mm) | Anode/filter | Tube voltage (kV) | Tube current–exposure time product (mAs) |
|---|---|---|---|---|---|---|
| Anna | Lorad Selenia | Amorphous selenium | 0.07 | W/Rh | 27 | 78 |
| Barbara | 32 | 92 | ||||
| Chris | Mammomat Inspiration | Amorphous selenium | 0.85 | W/Rh | 27 | 61 |
| Diana | 30 | 81 | ||||
| Elizabeth | 31 | 285 |
Acknowledgments
The authors thank the Jarvis Breast Screening Unit in Guildford and the Foundation of Population Screening East, in Nijmegen, for access to their mammography systems; Christian Fedon and the physics team from the Dutch Expert Centre for Screening (LRCB), in Nijmegen, for helping with the measurements; and, finally, Stephan Schopphoven and Ulf Mäder for providing information about the behavior and characteristics of the breast phantoms. The author Alistair Mackenzie was funded as part of the OPTIMAM2 project and is supported by Cancer Research UK (Grant No. C30682/A17321). This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Biographies
Joana Boita is a PhD student in the Department of Medical Imaging of the Radboud University Medical Center and at the Dutch Expert Centre for Screening (LRCB), with a background in biomedical engineering and in physics.
Alistair Mackenzie is a medical physicist at the Royal Surrey NHS Foundation Trust, where he is head of the National Co-ordinating Centre for the Physics of Mammography.
Ruben E. van Engen is a physics consultant at the Dutch Expert Centre for Screening (LRCB) and radiation protection expert. He coordinated the work on the physics chapters of the European guidelines in mammography, its supplement, and in EUREF.
Mireille Broeders is a professor in the Department for Health Evidence of the Radboud University Medical Center and is the scientific supervisor at the Dutch Expert Centre for Screening (LRCB).
Ioannis Sechopoulos is an associate professor in the Department of Medical Imaging of the Radboud University Medical Center, where he heads the Advanced X-ray Tomographic Imaging (AXTI) Laboratory and is a scientific advisor of the Dutch Expert Centre for Screening (LRCB).
Disclosures
Some of the authors of this paper declare relationships with companies. Ioannis Sechopoulos has research agreements with Siemens Healthcare, Canon Medical Systems, ScreenPoint Medical, Sectra Benelux, and Volpara Health Technologies and speaker agreements with Siemens Healthcare. Mireille Broeders has speaker agreements with Siemens Healthcare and Hologic. For the remaining authors, none were declared.
Contributor Information
Joana Boita, Email: joana.dossantosboita@radboudumc.nl.
Alistair Mackenzie, Email: alistairmackenzie@nhs.net.
Ruben E. van Engen, Email: r.vanengen@lrcb.nl.
Mireille Broeders, Email: mireille.broeders@radboudumc.nl.
Ioannis Sechopoulos, Email: ioannis.sechopoulos@radboudumc.nl.
References
- 1.Pisano E. D., et al. , “Diagnostic performance of digital versus film mammography for breast-cancer screening,” N. Engl. J. Med. 353(17), 1773–1783 (2005). 10.1056/NEJMoa052911 [DOI] [PubMed] [Google Scholar]
- 2.Mackenzie A., et al. , “Breast cancer detection rates using four different types of mammography detectors,” Eur. Radiol. 26(3), 874–883 (2016). 10.1007/s00330-015-3885-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Saunders R. S., et al. , “Does image quality matter? Impact of resolution and noise on mammographic task performance,” Med. Phys. 34(10), 3971–3981 (2007). 10.1118/1.2776253 [DOI] [PubMed] [Google Scholar]
- 4.Ruschin M., et al. , “Dose dependence of mass and microcalcification detection in digital mammography: free response human observer studies,” Med. Phys. 34(2), 400–407 (2007). 10.1118/1.2405324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Feig S. A., “Image quality of screening mammography: effect on clinical outcome,” Am. J. Roentgenol. 178(4), 805–807 (2002). 10.2214/ajr.178.4.1780805 [DOI] [PubMed] [Google Scholar]
- 6.Mackenzie A., et al. , “The relationship between cancer detection in mammography and image quality measurements,” Phys. Medica 32(4), 568–574 (2016). 10.1016/j.ejmp.2016.03.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Burgess A. E., “Effect of detector element size on signal detectability in digital mammography,” Proc. SPIE 5745, 232–242 (2005). 10.1117/12.593770 [DOI] [Google Scholar]
- 8.Samei E., et al. , “Digital mammography: effects of reduced radiation dose on diagnostic performance,” Radiology 243(2), 396–404 (2007). 10.1148/radiol.2432061065 [DOI] [PubMed] [Google Scholar]
- 9.Yaffe M. J., et al. , “Comparative performance of modern digital mammography systems in a large breast screening program,” Med. Phys. 40(12), 121915 (2013). 10.1118/1.4829516 [DOI] [PubMed] [Google Scholar]
- 10.Metz C. E., “Receiver operating characteristic analysis: a tool for the quantitative evaluation of observer performance and imaging systems,” J. Am. Coll. Radiol. 3(6), 413–422 (2006). 10.1016/j.jacr.2006.02.021 [DOI] [PubMed] [Google Scholar]
- 11.Chakraborty D. P., Berbaum K. S., “Observer studies involving detection and localization: modeling, analysis, and validation,” Med. Phys. 31(8), 2313–2330 (2004). 10.1118/1.1769352 [DOI] [PubMed] [Google Scholar]
- 12.Obuchowski N. A., Lieber M. L., Powell K. A., “Data analysis for detection and localization of multiple abnormalities with application to mammography,” Acad. Radiol. 7(7), 516–525 (2000). 10.1016/S1076-6332(00)80324-4 [DOI] [PubMed] [Google Scholar]
- 13.Obuchowski N. A., “How many observers are needed in clinical studies of medical imaging?” Am. J. Roentgenol. 182(4), 867–869 (2004). 10.2214/ajr.182.4.1820867 [DOI] [PubMed] [Google Scholar]
- 14.Bakic P. R., et al. , “Virtual tools for the evaluation of breast imaging: state-of-the science and future directions,” Lect. Notes Comput. Sci. 9699, 518–524 (2016). 10.1007/978-3-319-41546-8_65 [DOI] [Google Scholar]
- 15.Hadjipanteli A., et al. , “The threshold detectable mass diameter for 2D-mammography and digital breast tomosynthesis,” Phys. Medica 57, 25–32 (2019). 10.1016/j.ejmp.2018.11.014 [DOI] [PubMed] [Google Scholar]
- 16.Timberg P., et al. , “Visibility of microcalcification clusters and masses in breast tomosynthesis image volumes and digital mammography: a 4AFC human observer study,” Med. Phys. 39(5), 2431–2437 (2012). 10.1118/1.3694105 [DOI] [PubMed] [Google Scholar]
- 17.Salvagnini E., et al. , “Impact of compressed breast thickness and dose on lesion detectability in digital mammography: FROC study with simulated lesions in real mammograms,” Med. Phys. 43(9), 5104–5116 (2016). 10.1118/1.4960630 [DOI] [PubMed] [Google Scholar]
- 18.Ikejimba L. C., et al. , “A four-alternative forced choice (4AFC) methodology for evaluating microcalcification detection in clinical full-field digital mammography (FFDM) and digital breast tomosynthesis (DBT) systems using an inkjet-printed anthropomorphic phantom,” Med. Phys. 46(9), 3883–3892 (2019). 10.1002/mp.13629 [DOI] [PubMed] [Google Scholar]
- 19.Badal A., Clark M., Ghammraoui B., “Reproducing two-dimensional mammograms with three-dimensional printed phantoms,” J. Med. Imaging 5(3), 033501 (2018). 10.1117/1.JMI.5.3.033501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zanca F., et al. , “Evaluation of clinical image processing algorithms used in digital mammography,” Med. Phys. 36(3), 765–775 (2009). 10.1118/1.3077121 [DOI] [PubMed] [Google Scholar]
- 21.Warren L. M., et al. , “Effect of image quality on calcification detection in digital mammography,” Med. Phys. 39(6), 3202–3213 (2012). 10.1118/1.4718571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Glick S. J., Ikejimba L. C., “Advances in digital and physical anthropomorphic breast phantoms for x-ray imaging,” Med. Phys. 45(10), e870–e885 (2018). 10.1002/mp.13110 [DOI] [PubMed] [Google Scholar]
- 23.Saunders R. S., “A method for modifying the image quality parameters of digital radiographic images,” Med. Phys. 30(11), 3006–3017 (2003). 10.1118/1.1621870 [DOI] [PubMed] [Google Scholar]
- 24.Mackenzie A., et al. , “Conversion of mammographic images to appear with the noise and sharpness characteristics of a different detector and x-ray system,” Med. Phys. 39(5), 2721–2734 (2012). 10.1118/1.4704525 [DOI] [PubMed] [Google Scholar]
- 25.Mackenzie A., et al. , “Image simulation and a model of noise power spectra across a range of mammographic beam qualities,” Med. Phys. 41(12), 121901 (2014). 10.1118/1.4900819 [DOI] [PubMed] [Google Scholar]
- 26.Svalkvist A., Båth M., “Simulation of dose reduction in tomosynthesis,” Med. Phys. 37(1), 258–269 (2010). 10.1118/1.3273064 [DOI] [PubMed] [Google Scholar]
- 27.Båth M., et al. , “Method of simulating dose reduction for digital radiographic systems,” Radiat. Prot. Dosimetry 114(1–3), 253–259 (2005). 10.1093/rpd/nch540 [DOI] [PubMed] [Google Scholar]
- 28.Mackenzie A., et al. , “A method to modify mammography images to a appear as if acquired using different radiographic factors,” Proc. SPIE 10948, 109482F (2019). 10.1117/12.2512419 [DOI] [Google Scholar]
- 29.Boita J., Mackenzie A., Sechopoulos I., “Breast phantom validation of a mammographic image modification method,” Proc. SPIE 10718, 107180P (2018). 10.1117/12.2318367 [DOI] [Google Scholar]
- 30.Boita J., Mackenzie A., Sechopoulos I., “Validation of a method to simulate the acquisition of mammographic images with different techniques,” Proc. SPIE 10948, 109481K (2019). 10.1117/12.2513393 [DOI] [Google Scholar]
- 31.Moore A. C., et al. , “The commissioning and routine testing of mammographic x-ray systems,” IPEM Rep. 89 (2005).
- 32.IEC, “Medical electrical equipment-characteristics of digital x-ray imaging devices-part 1-2: determination of detective quantum efficiency detectors used in mammography,” IEC 62220-1-2, International Electrotechnical Commission; (2007). [Google Scholar]
- 33.Carton A.-K., et al. , “The effect of scatter and glare on image quality in contrast-enhanced breast imaging using an a-Si/CsI(TI) full-field flat panel detector,” Med. Phys. 36(3), 920–928 (2009). 10.1118/1.3077922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Marshall N. W., “Retrospective analysis of a detector fault for a full field digital mammography system,” Phys. Med. Biol. 51(21), 5655–5673 (2006). 10.1088/0031-9155/51/21/018 [DOI] [PubMed] [Google Scholar]
- 35.Dobbins J. T., et al. , “Intercomparison of methods for image quality characterization. II. Noise power spectrum,” Med. Phys. 33(5), 1454 (2006). 10.1118/1.2188819 [DOI] [PubMed] [Google Scholar]
- 36.Maidment A. D. A., Albert M., “Conditioning data for calculation of the modulation transfer function,” Med. Phys. 30(2), 248–253 (2003). 10.1118/1.1534111 [DOI] [PubMed] [Google Scholar]
- 37.Schopphoven S., et al. , “Breast phantoms for 2D digital mammography with realistic anatomical structures and attenuation characteristics based on clinical images using 3D printing,” Phys. Med. Biol. 64(21), 215005 (2019). 10.1088/1361-6560/ab3f6a [DOI] [PubMed] [Google Scholar]
- 38.Caldwell C. B., Yaffe M. J., “Development of an anthropomorphic breast phantom,” Med. Phys. 17(2), 273–280 (1990). 10.1118/1.596506 [DOI] [PubMed] [Google Scholar]
- 39.Looney P., et al. , “Sampling probability distributions of lesions in mammograms,” Proc. SPIE 9418, 94180R (2015). 10.1117/12.2081905 [DOI] [Google Scholar]