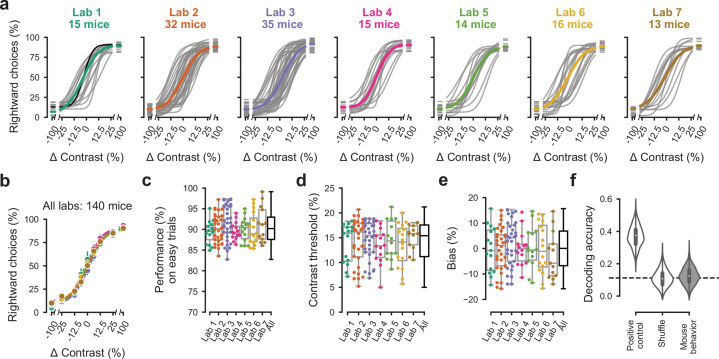
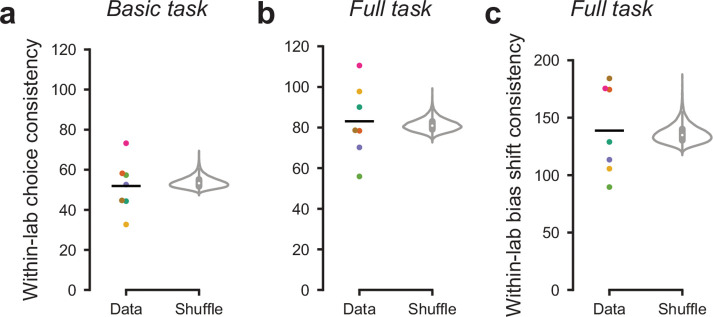
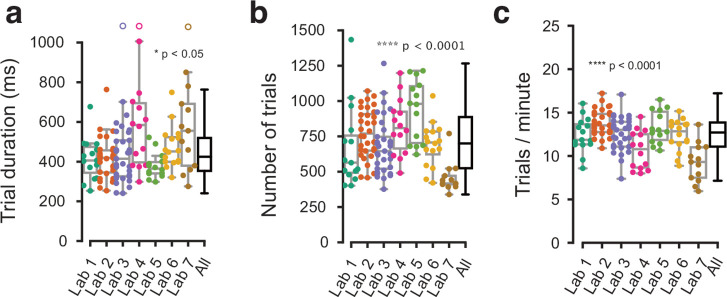
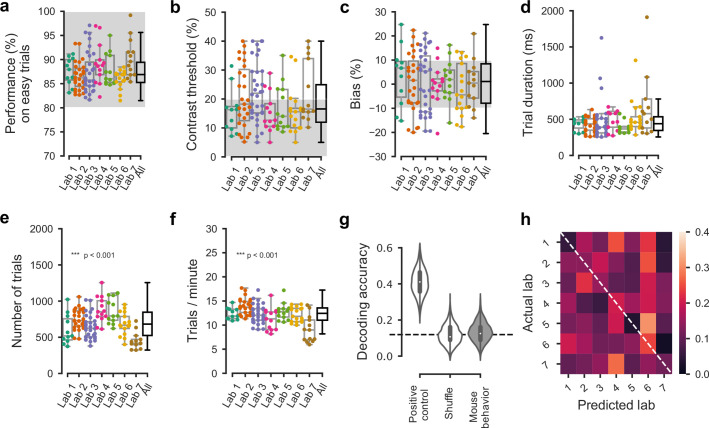
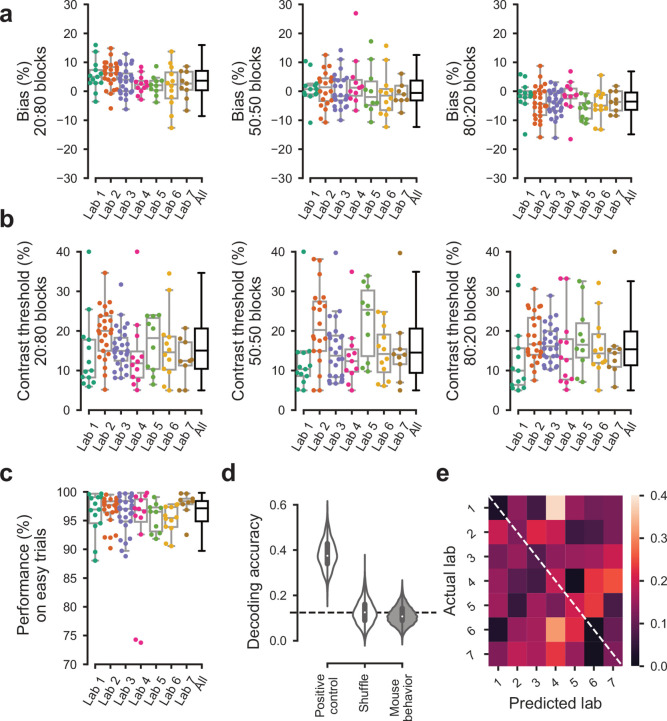
Figure 3. Performance in the basic task was indistinguishable across laboratories.
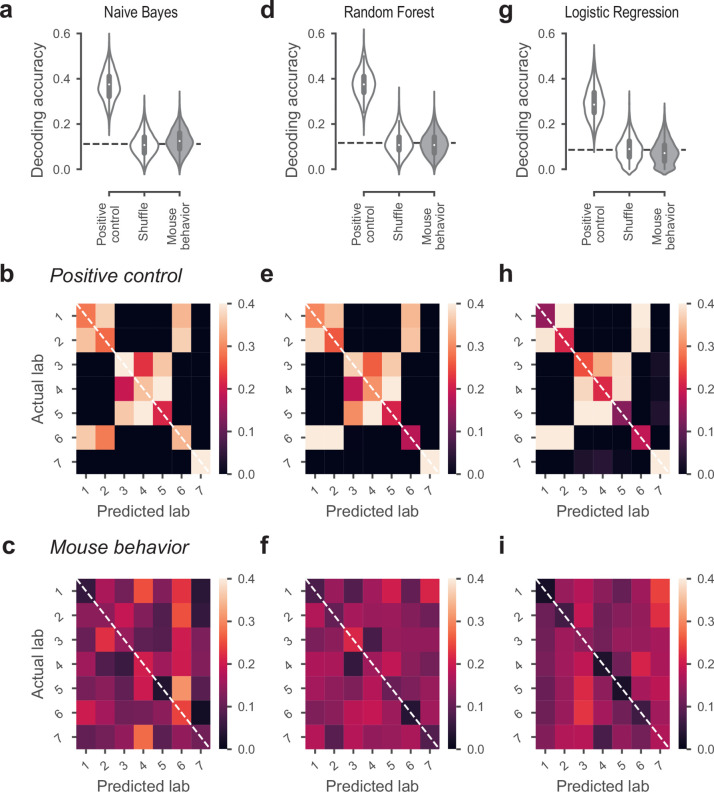
(a) Psychometric curves across mice and laboratories for the three sessions at which mice achieved proficiency on the basic task. Each curve represents a mouse (gray). Black curve represents the example mouse in Figure 1. Thick colored lines show the lab average. (b) Average psychometric curve for each laboratory. Circles show the mean and error bars ± 68% CI. (c) performance on easy trials (50% and 100% contrasts) for each mouse, plotted per lab and over all labs. Colored dots show individual mice and boxplots show the median and quartiles of the distribution. (d-e) Same, for contrast threshold and bias. (f) Performance of a Naive Bayes classifier trained to predict from which lab mice belonged, based on the measures in (c-e). We included the timezone of the laboratory as a positive control and generated a null-distribution by shuffling the lab labels. Dashed line represents chance-level classification performance. Violin plots: distribution of the 2000 random sub-samples of eight mice per laboratory. White dots: median. Thick lines: interquartile range.