Figure 7. Embryonic V1^R firing patterns predicted by computational modeling.

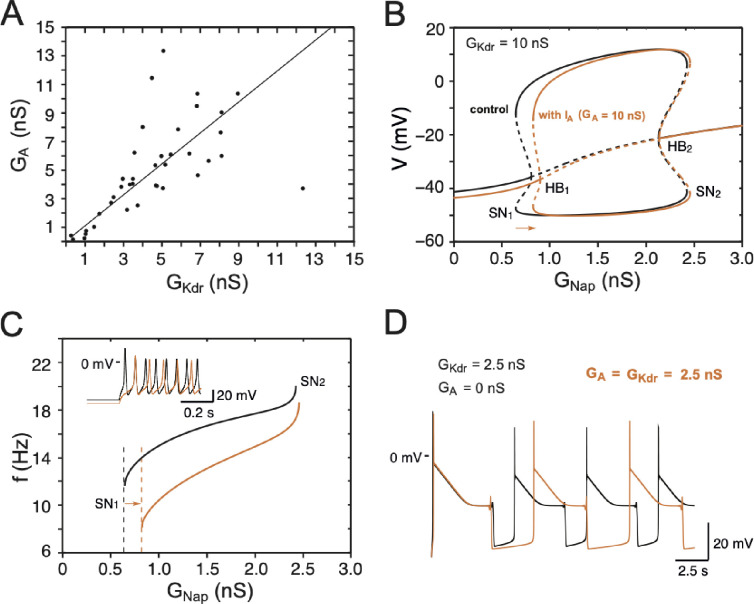
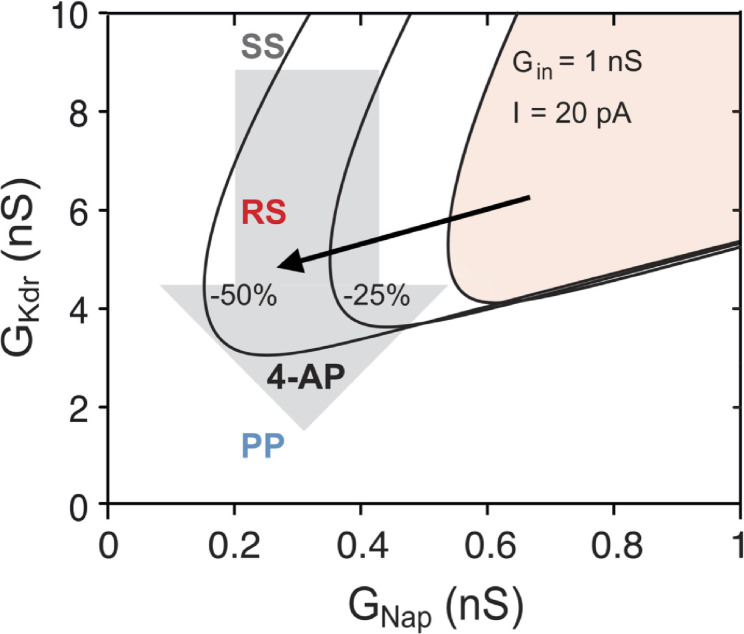
(A) Firing patterns of 26 recorded cells, in which both ${\displaystyle G_{Nap}}$ and ${\displaystyle G_{Kdr}}$ were measured. Gray: single spiking (SS); red: repetitive spiking (RS); blue: plateau potential (PP). The three purple points located at the boundary between the RS and PP regions correspond to mixed events (ME), where plateau potentials alternate with spiking episodes. Note that no cell exhibited low values of both ${\displaystyle G_{Nap}}$ and $G_{Kdr}$ (lower left) or large values of both conductances (upper right). (B) Bifurcation diagram of the deterministic model when ${\displaystyle G_{Kdr}}$ is kept fixed to 2.5 nS or 10 nS while ${\displaystyle G_{Nap}}$ is varied between 0 and 2.5 nS. ${\displaystyle G_{in}}$ = 1 nS and ${\displaystyle I}$ = 20 pA. For ${\displaystyle G_{Kdr}}$ = 10 nS (i.e., in the top experimental range), the red curves indicate the maximal and minimal voltages achieved on the stable limit cycle associated with repetitive firing (solid lines) and on the unstable limit cycle (dashed lines). The fixed point of the model is indicated by a gray solid line when it corresponds to the stable quiescent state, a gray dashed line when it is unstable, and a solid blue line when it corresponds to a stable plateau potential. The two Hopf bifurcations (HB) corresponding to the change of stability of the quiescence state (HB₁, $G_{Nap}$ = 0.81 nS) and the voltage plateau (HB₂, $G_{Nap}$ = 2.13 nS) are indicated, as well as the two saddle node (SN) bifurcations of limit cycles associated with the onset (SN₁, $G_{Nap}=$ 0.65 nS) and offset (SN₂, $G_{Nap}$ = 2.42 nS) of repetitive spiking as ${\displaystyle G_{Nap}}$ is increased. For ${\displaystyle G_{Kdr}}$ = 2.5 nS, the model does not display repetitive firing; it possesses a unique fixed point, which is always stable (blue-gray curve). The transition from quiescence to plateau is gradual with no intervening bifurcation. Representative voltage traces of the three different activity patterns are shown: SS in response to a 2 s current pulse (gray, ${\displaystyle G_{Nap}}$= 0.2 nS, ${\displaystyle G_{Kdr}}$= 10 nS), RS (red, ${\displaystyle G_{Nap}}$= 1.2 nS, ${\displaystyle G_{Kdr}}$= 10 nS), and PP (blue, ${\displaystyle G_{Nap}}$= 1.2 nS, ${\displaystyle G_{Kdr}}$= 2.5 nS). Note that the plateau never outlasts the current pulse. (C) Bifurcation diagram when ${\displaystyle G_{Nap}}$ is kept fixed at 1.2 nS and ${\displaystyle G_{Kdr}}$ is varied between 0 and 25 nS (${\displaystyle I}$ = 20 pA). Same conventions as in (B). PP is stable until the subcritical HB₂ ($G_{Kdr}$ = 6.34 nS) is reached, repetitive firing can be observed between SN₂ ($G_{Kdr}$ = 5.93 nS) and SN₁ ($G_{Kdr}$ = 22.65 nS). The quiescent state is stable from point HB₁ (${\displaystyle G_{Kdr}}$= 17.59 nS) onward. (D) Two-parameter bifurcation diagram of the model in the ${\displaystyle G_{Nap}}$ - ${\displaystyle G_{Kdr}}$ plane (${\displaystyle I}$ = 20 pA). The black curves indicate the bifurcations HB₁ and HB₂. The red curves indicate the SN bifurcations of limit cycles SN₁ and SN₂. The shaded area indicates the region where repetitive firing can occur. The oblique lines through the points labeled 1, 2, and 3, the same as in (B), correspond to three different values of the ratio of ${\displaystyle G_{Nap}}$ / $G_{Kdr}$: 0.02 (gray), 0.12 (red), and 0.48 (blue). Voltage traces on the right display the response to a 2 s current pulse when channel noise is taken into account for the three regimes: SS (top, gray trace and dot in the diagram), RS (middle, red), and PP (bottom, blue). They correspond to the three deterministic voltage traces shown in (B). Note that the one-parameter bifurcation diagrams shown in (B) correspond to horizontal lines through points 1 and 2 ($G_{Kdr}$ = 10 nS) and through point 3 (${\displaystyle G_{Kdr}}$ = 2.5 nS), respectively. The bifurcation diagram in (C) corresponds to a vertical line through points 2 and 3 (${\displaystyle G_{Nap}}$ = 1.2 nS). (E) Cumulative distribution function of the ratio ${\displaystyle G_{Nap}/G_{Kdr}}$ for the four clusters in (A), showing the sequencing SS (gray) → RS (red) → ME (purple, three cells only) → PP (blue) predicted by the two-parameter bifurcation diagram in (D). The wide PP range, as compared to SS and RS, merely comes from the fact that $G_{Kdr}$ is small for cells in this cluster. The three colored points indicate the slopes of the oblique lines displayed in (D) . (F) The data points in (A) are superimposed on the two-parameter bifurcation diagram shown in (D), demonstrating a good agreement between our basic model and experimental data (same color code as in A for the different clusters). The bifurcation diagram is simplified compared to (A), only the region where repetitive spiking is possible (i.e., between the lines SN₁ and SN₂ in A) being displayed (shaded area). Notice that three ME cells (purple dots) are located close to the transition between the RS and PP regions. The four arrows indicate the presumable evolution of ${\displaystyle G_{Nap}}$ and ${\displaystyle G_{Kdr}}$ for SS, RS, ME, and PP cells between E12.5 and E14.5–15.5. ${\displaystyle G_{Nap}}$ eventually decreases while $G_{Kdr}$ keeps on increasing. (G) Distribution of a sample of cells in the ${\displaystyle G_{Nap}}$ - ${\displaystyle G_{Kdr}}$ plane at E14.5. All the cells are located well within the SS region far from bifurcation lines because of the decreased ${\displaystyle G_{Nap}}$ compared to E12.5, the increased ${\displaystyle G_{Kdr}}$, and the shift of the RS region (shaded) due to capacitance increase (18 versus 13 pF).

Figure 7—figure supplement 1. Effect of ${\displaystyle I_A}$ on embryonic V1^R firing patterns predicted by computational modeling.

(A) The maximal conductances of ${\displaystyle I_{Kdr}}$ and ${\displaystyle I_A}$ at E12.5 are linearly correlated. Best fit: ${\displaystyle G_A}$ = 1.09 ${\displaystyle G_{Kdr}}$ (R² = 0.81, N = 44). (B) Effect of ${\displaystyle I_A}$ on the dynamics of the basic model. The one-parameter bifurcation diagrams in control condition (black, ${\displaystyle I}$ = 20 pA, ${\displaystyle G_{Kdr}}$ = 10 nS, no $I_A,$ same as in Figure 7B) and with ${\displaystyle I_A}$ added (orange, ${\displaystyle G_A}$ = 10 nS) are superimposed. The $I_A$ current shifts the firing threshold SN₁ to the right by 0.18 nS (see also C) as indicated by the orange arrow, with little effect on the amplitude of action potentials (see also inset in C). In contrast, $I_A$ shifts SN₂ by only 0.03 nS because it is inactivated by depolarization. (C) ${\displaystyle I_A}$ also slows down the discharge frequency, as shown by comparing the ${\displaystyle G_{Nap}-V}$ curves without $I_A$ (black) and with ${\displaystyle I_A}$ (orange). For ${\displaystyle G_{Nap}}$ = 1 nS, for instance, the firing frequency is reduced by 31%, from 15 to 10.4 Hz. Here again, the effect of ${\displaystyle I_A}$ progressively decreases as ${\displaystyle G_{Nap}}$ increases because of the membrane depolarization elicited by ${\displaystyle I_{Nap}}$. For ${\displaystyle G_{Nap}}$ = 2.4 nS, for instance, the firing frequency is reduced by 11% only, from 19.1 to 17 Hz. This frequency reduction elicited by $I_A$ does not merely result from the increased firing threshold. Note also that the latency of the first spike is increased (see voltage trace in inset), which is a classical effect of $I_A$. (D) $I_A$ reduces the frequency of pseudo-plateau bursting by lengthening quiescent episodes (doubling their duration in the example shown) without affecting the duration of plateaus much (here a mere 5% increase), as shown by the comparison of the voltage traces obtained without ${\displaystyle I_A}$ (control, ${\displaystyle G_{Kdr}}$= 2.5 nS, black) and with${\displaystyle I_A}$ (${\displaystyle G_{Kdr}=G_A=}$ 2.5 nS, orange). This is because ${\displaystyle I_A}$ is activated near rest but inactivated during voltage plateaus. Note that increasing ${\displaystyle G_{Kdr}}$ in the absence of ${\displaystyle I_A}$ has not the same effect; it shortens both plateaus and quiescent episodes (see Figure 8C, where ${\displaystyle G_{Kdr}}$= 5 nS). This is because ${\displaystyle I_{Kdr}}$ does not inactivate (or does it only very slowly) in contrast to ${\displaystyle I_A}$.

Figure 7—figure supplement 2. Explaining the effect of 4-aminopiridine (4-AP) on the firing pattern.

The R region of the basic model, where repetitive firing may occur, is displayed in the ${\displaystyle G_{Nap}-G_{Kdr}}$ plane in control condition for E12.5 V1^R (${\displaystyle C_{in}}$ = 13 pF, ${\displaystyle G_{in}}$ = 1 nS, ${\displaystyle I}$ = 20 pA, shaded area) and when ${\displaystyle G_{in}}$ and $I$ were both reduced by 25% (middle curve) or 50% (left curve). The reduced ${\displaystyle I}$ accounts for the decrease in rheobase, and thus in the current injected in the experiments, following the decrease in ${\displaystyle G_{in}}$. If 4-AP reduced only $G_{Kdr}$ (as indicated by the downward arrow), the firing pattern of SS V1^R would not change, the RS region being too far to the right to be visited. In contrast, when the effects of 4-AP on the input conductance and rheobase are taken into account, the bifurcation diagram moves leftward and downward, as indicated by the oblique black arrow, and the RS and PP regions are then successively entered as $G_{Kdr}$ is reduced. The same explanation holds at E14.5.