Figure 1:

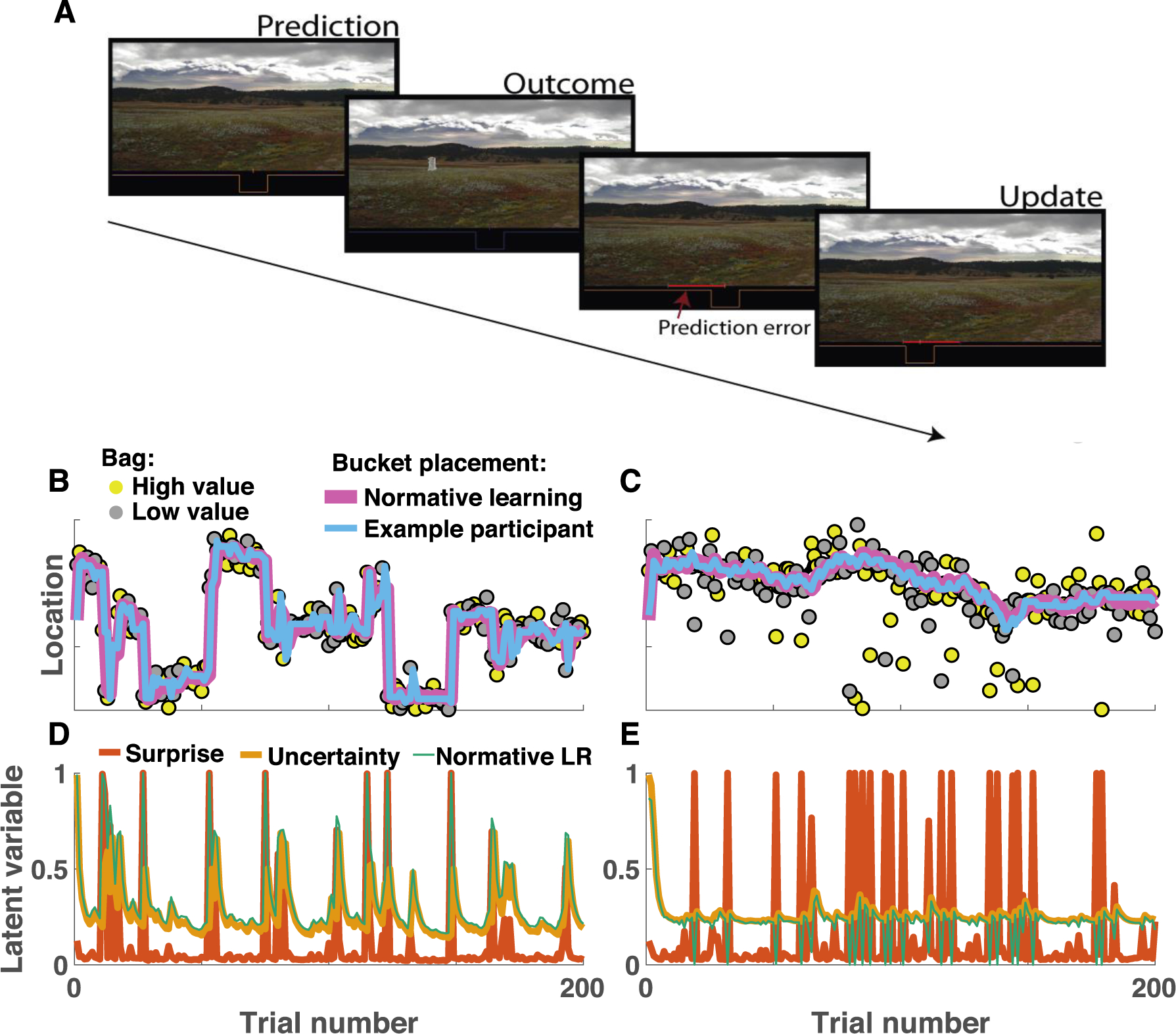
Predictive inference task measures learning in different statistical contexts. A) On each trial, participants were required to adjust the position of a bucket to catch bags of coins that would be dropped from an unobservable helicopter. Subjects were not able to observe the helicopter, and thus forced to use the history of bag locations and knowledge about the environmental statistics to inform bucket placement. B-C) Example data from a single subject performing the predictive inference task in changepoint (B) and oddball (C) conditions. B) In the changepoint condition, the helicopter (not shown) remained in a single screen position (ordinate) for a number of trials (abscissa), before occasionally relocating to a new screen position (changepoint). Bag locations (yellow and gray points) were drawn from a normal distribution centered on the helicopter location. Inferences about the helicopter location made by a normative learning model (pink line) and bucket placements made by an example subject (blue line) are both rapid to adjust after changepoints in the helicopter location. C) In the oddball condition, the helicopter position drifted slowly from one trial to the next, and bag positions were either drawn from a normal distribution centered on the helicopter location (90% of trials) or a uniform distribution across the entire task space (10% of trials). D&E) The normative learning model adjusted learning rate (green line) on each trial according to uncertainty (yellow) and surprise (orange). In the changepoint condition (D) surprise was indicative of changepoints and increased learning rates, whereas in the oddball condition (E) surprise was indicative of an uninformative oddball and thus promoted lower learning rates.