An arbitrary Lagrangian Eulerian smoothed particle hydrodynamics (ALE-SPH) method with a boundary volume fraction formulation for fluid-structure interaction

Abstract

We present a new weakly-compressible smoothed particle hydrodynamics (SPH) method capable of modeling non-slip fixed and moving wall boundary conditions. The formulation combines a boundary volume fraction (BVF) wall approach with the transport-velocity SPH method. The resulting method, named SPH-BVF, offers detection of arbitrarily shaped solid walls on-the-fly, with small computational overhead due to its local formulation. This simple framework is capable of solving problems that are difficult or infeasible for standard SPH, namely flows subject to large shear stresses or at moderate Reynolds numbers, and mass transfer in deformable boundaries. In addition, the method extends the transport-velocity formulation to reaction-diffusion transport of mass in Newtonian fluids and linear elastic solids, which is common in biological structures. Taken together, the SPH-BVF method provides a good balance of simplicity and versatility, while avoiding some of the standard obstacles associated with SPH: particle penetration at the boundaries, tension instabilities and anisotropic particle alignments, that hamper SPH from being applied to complex problems such as fluid-structure interaction in a biological system.

1. Introduction

Smoothed particle hydrodynamics (SPH) is a meshless particle method based on a Lagrangian formulation [1], proposed independently by Gingold and Monaghan [2] and Lucy [3] as a method to simulate astrophysical problems. Since its development, SPH has been used in a wide range of applications, including colloidal suspensions [4, 5], nanofluidics [6], blood flow [7, 8], multiphase flows [9], polymer chains [10] and red blood cell deformations [11].

In contrast to grid-based methods, SPH uses a kernel estimation at Lagrangian points (particles) to approximate the partial differential equations (PDEs) that govern the system of interest. When compared with standard mesh-based methods,such as finite element (FEM), finite difference (FDM) and finite volume (FVM), SPH offers attractive advantages. As a consequence of its Lagrangian description, advection is treated exactly, allowing the simulation of arbitrary free-shear flow in systems with complex geometries without the need to use an adaptive mesh or interface tracking [12, 13]. Another important feature of the method is its inherent adaptivity, as particle attributes evolve according to their material time derivative [14]. More recently, the development of multi-resolution SPH brings the method closer to industrial applications by adaptively increasing the resolution by means of splitting particles in regions of interest, and coalescing particles in regions where lower resolutions suffices [15, 16, 17, 18, 19].

Despite all of these advantages, the treatment of solid wall boundaries in SPH remains a challenge. Recent studies [20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30] have demonstrated that despite several improvements, the development of a robust, efficient and accurate method capable of preventing particle penetration under no-slip and partial-slip conditions remains an open problem. In fact, some consider it to be one of the grand challenges for the advancement of SPH [31].

The work of Valizadeh and Monaghan [32] provides a comprehensive review of the available solid wall models, comparing the performance of the most widely-used strategies and highlighting their capabilities and drawbacks. They classify the different models of solid boundaries into three main groups: (i) semi-analytical, (ii) ghost particles and (iii) boundary force methods. In the semi-analytical approach [25], surface integrals must be approximated using the SPH formalism. A limitation of this class of methods is the complexity of the algorithm, as many modifications are necessary to help prevent particle penetration on the solid boundary. In the ghost particles approach [33], a set of fictitious particles are created in the wall in order to guarantee non-slip and prevent penetration. Despite being conceptually attractive, the treatment of complex geometries is not straightforward. Similarly challenging, the computational algorithm typically requires the creation/destruction of particles at specific wall positions at each time step, causing memory access overheads and additional communication in otherwise parallel tasks.

These limitations make the class of boundary force methods a simple and attractive alternative. As a common feature, these methods use predetermined layers of particles to model boundaries. The variants in this class differ in the way velocity and density are communicated between wall and fluid particles. For example, in the method developed by Monaghan and Kajtar [23], a Lennard-Jones boundary force is added to the momentum equation for particles in the neighborhood of the walls, in a similar manner as the forces used in the immersed boundary method [34]. This approach, despite its simplicity, is effective for a wide range of problems, provided that all the parameters of the boundary force are calibrated correctly.

In the work of Adami et al. [22], the pressure and velocity of boundary particles are computed using interpolation of the fluid field, thus implicitly enforcing the impermeability condition of rigid walls. Unlike the method of Monaghan and Kajtar [23], this method does not require parameter calibration. In fact, the detailed study of Valizadeh and Monaghan [32] concluded that the method of Adami et al. [22] is overall the best method available. More recently, Khayyer et al. [35] obtained good results for an enhanced incompressible SPH method and a pressure-based, physically-derived boundary condition. Similarly, Zhan et al. [36] obtained excellent results and nearly quadratic convergence by using stabilization techniques to achieve higher accuracy. However, both frameworks used the boundary condition proposed by Adami et al. [22] in which there is no mathematical guarantee that particle penetration is prevented.

Recently a new method, designed primarily for dissipative particle dynamics (DPD) systems, was proposed by Li et al. [37]. This method introduces an indicator variable, which measures the boundary volume fraction (BVF) of particles near solid walls, and employs a predictor-corrector integration to prevent particle penetration. As a result, the fluid particles become autonomous to find wall surfaces in arbitrarily shaped objects, based solely on the coordinates of their neighboring particles. Thus, this method prevents particle penetration with minimal computational overhead by using a local formulation.

In this context we propose a new SPH formulation combining the BVF wall treatment with the transport-velocity discretization. The resulting method, named SPH-BVF, is versatile, accurate and allows the modeling of fixed and moving boundaries. In contrast to the method proposed by Adami et al. [22], the impermeability is explicitly enforced during the time integration, and no further correction of the pressure field is required. Furthermore, we improve the BVF method for the case of moving boundaries by using weighted interpolations of the solid particles to determine the wall velocity and accelerations, resulting in an algorithm capable of dealing with deforming boundaries. Finally, we introduce the reaction-diffusion equation in our formulation, extending the usage of the method to conjugate mass transport problems in moving boundaries, enabling simulations where boundary deformations are caused by reaction-diffusion events. This step is crucial in enabling SPH to simulate certain biological systems in which enzymatic reactions trigger processes that modify the boundary properties.

The main features of the SPH-BVF method include (a) algorithmic simplicity; (b) retaining the locality and intrinsic parallelism of the SPH method at the cost of a small overhead; (c) preventing the three major problems in standard SPH methods: particle penetration at the boundaries, tension instabilities and anisotropic structures. We demonstrate these capabilities and validate the proposed method using canonical examples and compare the results with the literature. Finally, we test the new method on a biomechanical cell wall polarization problem that incorporates multiple physics (species transport, solid and fluid mechanics), and thus could not be solved by existing SPH methods and remains challenging for advanced commercial multiphysics FEM tools.

This paper is organized as follows: Section 2 briefly describes the transport-velocity SPH formulation. Section 3 provides the additional equations required for the SPH-BVF method and its algorithm. Sections 4 and 5 present validations, applications, and discussion of relevant results. Finally, conclusions and future perspectives are discussed in Section 6.

2. SPH formulation

In this section we provide a brief overview of the governing equations, the SPH discretizations and the temporal integration method proposed.

2.1. Governing equations and transport-velocity formulation

The continuum mechanics equations for the conservation of mass, linear momentum and concentration of species in a Lagrangian reference frame are given by

$$\frac{d\rho }{dt}=-\rho \nabla \cdot \mathit{v},$$ (1)

$$\frac{d\mathit{v}}{dt}=\frac{1}{\rho }\nabla \cdot \sigma +{\mathit{F}}_{\mathrm{B}},$$ (2)

$$\frac{dC}{dt}=\nabla \cdot (\alpha \nabla C)+R,$$ (3)

where ρ, v, σ, F_B, C, α and R denote the fluid density, velocity, Cauchy stress tensor, body force, concentration, mass diffusivity and reaction term, respectively. The d(·)/dt operator denotes the material derivative [38].

One of the most relevant problems of standard, purely Lagrangian SPH discretizations of Eqs. (1)-(3) is the onset of anisotropic particle structures formed as the particles follow the Lagrangian trajectories. This problem was first addressed by Nestor et al. [39] by introducing the concept of particle shifting, where a small perturbation is inserted to the particle trajectories, reducing the formation of anisotropic structures. Later, the work of Shadloo et al. [40] applied particle shifting to a weakly compressible SPH formulation, obtaining improved results in fluid flow problems. More recent improvements include the usage of particle shifting in free surface flows for incompressible SPH formulations [41], and stabilized particle shifting techniques [42]. Oger et al. [43] clarified that this issue is particularly relevant in fluid flows in which there is a natural tendency of particle alignment, such as flows subject to stretching and shear stresses. A similarly relevant problem is the so-called tensile instability, a phenomenon that causes particles to clump when subject to a tension stress state [44], being particularly relevant in fluid-structure interactions, solids under large deformations and flows under high Reynolds numbers. Incidentally, both of these limiting issues are alleviated by using the transport-velocity formulation, proposed by Adami et al. [22] for fluids and later extended to solid mechanics by Zhang et al. [45]. The transport-velocity formulation consists of a particular type of Arbitrary Lagrangian Eulerian (ALE) formalism [43], where particles are advected by an arbitrary transport velocity, specifically tuned so that the pressure field is kept positive, thus avoiding the tensile instability, while at the same time it causes a small shift in the particle trajectories, avoiding the formation of coherent structures of particles. For a detailed numerical analysis of the transport-velocity SPH formulation, we refer the reader to Litvinov et al. [46].

The transport-velocity equations are obtained by rewriting the material derivative operator for a particle moving with a modified advection velocity $\tilde{\mathit{v}}$ as

$$\frac{\tilde{d}(•)}{dt}=\frac{\partial (•)}{\partial t}+\tilde{\mathit{v}}\cdot \nabla (•).$$ (4)

The presence of the modified transport velocity, $\tilde{\mathit{v}}$, modifies the material derivative operator with two relative velocity terms, leading to the following identity

$$\frac{d(•)}{dt}=\frac{\tilde{d}(•)}{dt}+\nabla \cdot [(•)(\mathit{v}-\tilde{\mathit{v}})]-(•)\nabla \cdot (\mathit{v}-\tilde{\mathit{v}}),$$ (5)

where, due to the weakly compressible approximation [12, 45], it is safe to assume that $\nabla \cdot (\mathit{v}-\tilde{\mathit{v}})\approx 0$. Thus, the transport-velocity formulation of the conservation laws, Eqs. (1)-(3), yields

$$\frac{\tilde{d}\rho }{dt}=-\rho \nabla \cdot \mathit{v}-\nabla \cdot [\rho (\mathit{v}-\tilde{\mathit{v}})],$$ (6)

$$\frac{\tilde{d}\mathit{v}}{dt}=\frac{1}{\rho }\nabla \sigma +{\mathit{F}}_{\mathrm{B}}-\nabla \cdot [\mathit{v}(\mathit{v}-\tilde{\mathit{v}})],$$ (7)

$$\frac{\tilde{d}C}{dt}=\nabla \cdot (\alpha \nabla C)+R-\nabla \cdot [C(\mathit{v}-\tilde{\mathit{v}})].$$ (8)

Equations (6)-(8) form the set of governing equations of the SPH-BVF formulation. Additional conservation laws can be added as needed, using the identity provided by Eq. (5). Notice that this formulation can be seen as a generic version of SPH schemes for an arbitrary reference frame [43], where $\tilde{\mathit{v}}$ is the referential velocity. For instance, if $\tilde{\mathit{v}}=\mathit{v}$, Eqs. (6)-(8) reduce to the classical, purely Lagrangian formulation. In contrast, setting $\tilde{\mathit{v}}=0$ results in a formulation for an inertial (Eulerian) reference frame. In the following sections, we discuss the usage of $\tilde{\mathit{v}}$ and how this term is discretized.

2.2. SPH discretization

In SPH, the mapping between the primitive variables (mass, momentum and concentrations) and the discrete particle system is done using two different approximations: a radial basis function kernel interpolation and a quadrature approximation. The radial basis function kernel interpolation consists of approximating a continuous function $f:{\mathbb{R}}^3\mapsto \mathbb{R}$, defined at coordinates x in $\Omega \subseteq {\mathbb{R}}^3$, by the integral equation with a smoothing kernel function W with compact support h

$$f(\mathit{x})\approx {\int }_{\Omega }f({\mathit{x}}^{\prime })W(\mathit{x}-{\mathit{x}}^{\prime },h)d{\mathit{x}}^{\prime }.$$ (9)

The accuracy of the approximation in Eq. (9) depends on the choice of W. For the sake of simplicity, we have adopted in this work the Lucy kernel, proposed by Lucy [3], with x_ij = x − x′ and ξ = ∥x_ij∥₂/h denoting a generalized coordinate

$$W(\xi )=\{\begin{array}{cc}{\alpha }_D(1+3\xi )(1-\xi {)}^3,\hfill & \text{if}0\le \xi \le 1,\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (10)

and the spatial derivative

$$\nabla W=\frac{\mathit{x}}{x}\frac{dW}{d\xi },$$ (11)

where the normalization parameter α_D depends on the dimensionality of the problem:

$${\alpha }_D=\{\begin{array}{cc}5∕4h,\hfill & \text{if}1\mathrm{D},\hfill \\ 5∕\pi h^2,\hfill & \text{if}2\mathrm{D},\hfill \\ 105∕16\pi h^3,\hfill & \text{if}3\mathrm{D}.\hfill \end{array}\phantom{\}}$$ (12)

For details on choosing W, the reader may refer to the work of Xu and Deng [13]. The second approximation consists of rewriting the integral given by Eq. (9) as a discrete sum. The domain Ω is then discretized using N particles, each located at coordinates x_i. The kernel approximations of f and ∇f are given by

$$f_i\approx \sum _{j=1}^N\frac{m_j}{{\rho }_j}{f}_j{W}_{ij},$$ (13)

$$\nabla f_i\approx \sum _{j=1}^N\frac{m_j}{{\rho }_j}(f_j\pm f_i)\nabla W_{ij},$$ (14)

where m_j/ρ_j, ⟨f⟩_i and ⟨∇f⟩_i denote the number density (weight) of particle j, the kernel approximations of the field f(x) and its gradient at position x_i, respectively.

2.3. Stress description of solids and fluids

Equations (1)-(3) allow a common description of fluid and solid dynamics within the same framework [45]. This facilitates the treatment of multiple materials in complex physical problems, such as biological systems and multiphase flows. Different materials can then be modeled using different constitutive relations for the Cauchy stress tensor σ. For validation purposes, we use two types of materials: linear elastic solids and Newtonian fluids. Thus,

$$\sigma =\{\begin{array}{cc}-P\mathit{I}+\mathit{S},\hfill & \text{solids}.\hfill \\ -P\mathit{I}+2\eta ϵ,\hfill & \text{for fluids}.\hfill \end{array}\phantom{\}}$$ (15)

where P, η are the pressure and viscosity, and S, ϵ, I denote the deviatoric stress, strain and second-order identity tensors, respectively. Assuming Hooke’s law, the Jaumann rate of the deviatoric stress tensor S is given by [44]

$$\frac{d\mathit{S}}{dt}=2G\left[ϵ-\frac{1}{3}\text{Tr}(ϵ)\mathit{I}\right]+\mathit{S}\cdot {\omega }^T+\omega \cdot \mathit{S},$$ (16)

where G is the shear modulus and ω is the rotation tensor. The kernel approximations are used to discretize the spatial derivatives and primitive variables in the governing equations, Eqs. (1)-(3). The resulting equations are

$$\begin{gathered} \frac{d{\rho }_i}{dt}={\rho }_i\sum _j\frac{m_j}{{\rho }_j}\nabla W_{ij}\cdot {\mathit{v}}_{ij} \\ -\sum _j\frac{m_j}{{\rho }_j}\nabla W_{ij}\cdot [{\rho }_i({\mathit{v}}_i-{\tilde{v}}_i)+{\rho }_j({\mathit{v}}_j-{\tilde{\mathit{v}}}_j)], \end{gathered}$$ (17)

$$\begin{gathered} \frac{d{\mathit{v}}_{\mathit{i}}}{dt}=-\sum _j{m}_j\nabla W_{ij}\cdot \\ \cdot \left[\left(\frac{{\sigma }_i}{{\rho }_i^2}+\frac{{\sigma }_j}{{\rho }_j^2}\right)-\left(\frac{{\mathbf{A}}_i}{{\rho }_i^2}+\frac{{\mathbf{A}}_j}{{\rho }_j^2}\right)\right] \\ +\sum _j{m}_j\frac{{\mu }_{ij}}{{\rho }_i{\rho }_j(x_{ij}^2+ϵh^2)}\nabla W_{ij}\cdot {\mathit{v}}_{ij}, \end{gathered}$$ (18)

$$\begin{gathered} \frac{d{C}_{\mathit{i}}}{dt}=\sum _j{m}_j\frac{{\alpha }_{ij}(C_j-C_i)}{{\rho }_i{\rho }_j(x_{ij}^2+ϵh^2)}\nabla W_{ij}\cdot x_{ij} \\ -\sum _j\frac{m_j}{{\rho }_j}\nabla W_{ij}\cdot [C_i({\mathit{v}}_i-{\tilde{\mathit{v}}}_i)+C_j({\mathit{v}}_j-{\tilde{\mathit{v}}}_j)], \end{gathered}$$ (19)

$$\begin{gathered} \frac{d{S}_i}{dt}=2G\left[{ϵ}_i-\frac{1}{3}Tr({ϵ}_i)\mathit{I}\right]+{\mathit{S}}_i\cdot {\omega }_i^T \\ +{\omega }_i\cdot {\mathit{S}}_i, \end{gathered}$$ (20)

where the strain and rotation tensors for each particle i in Eq. (20) are given by

$${ϵ}_i=\sum _j\frac{m_j}{2{\rho }_j}[{\mathit{v}}_{ij}\otimes \nabla W_{ij}+({\mathit{v}}_{ij}\otimes \nabla W_{ij}{)}^T],$$ (21)

$${\omega }_i=\sum _j\frac{m_j}{2{\rho }_j}[{\mathit{v}}_{ij}\otimes \nabla W_{ij}-({\mathit{v}}_{ij}\otimes \nabla W_{ij}{)}^T],$$ (22)

and the summations are performed over all neighboring particles of particle i that are within the compact support of W, and v_ij = v_i − v_j. The term $\mathbf{A}=\rho \mathit{v}(\mathit{v}-\tilde{\mathit{v}})$ denote the relative velocity tensor. The shear viscosity and mass diffusion coefficients are averaged as μ_ij = 2μ_iμ_j/(μ_i + μ_j) and α_ij = 2α_iα_j/(α_i + α_j). A small constant ϵ = 0.01 is added to the denominators of Eqs. (18)-(19) to prevent singularities.

The second summation in Eq. (18), introduced by Morris et al. [47], improves the stability of the numerical method by acting as a diffusive term, while modeling the viscous force F_V, in a similar manner as the Von Neumann & Richtmyer’s artificial viscosity term used in most standard SPH formulations [2, 48, 49], and has been used even for elastic solids [44]. In the present work, we have adopted the artificial viscosity formulation, but it is important to emphasize that the artificial viscosity term Eq.(18) is still an active area of research, and to a certain extent and despite being widely used in the classic SPH literature, its application makes the method case-dependent. A promising alternative to the artificial term consists in reformulating the SPH convolution integrals by introducing only the sufficient amount of dissipation by means of using a non-linear Riemann problem; this technique, named Godunov SPH (GSPH), is known for achieving very low advection and angular momentum conservation errors and no excessive diffusion, without the need for tuning artificial viscosity terms [50, 51, 52].

The model described by Eqs. (17)-(19) is closed by a relationship between the density and pressure field. For fluids, two different approaches are widely used in the literature, namely: 1) treat the flow as incompressible, either by solving a pressure-Poisson equation to obtain a divergence-free velocity field [53, 41], or by requiring as a kinematic constraint that the volume of the fluid particles is constant [54]; or 2) treat it as weakly compressible, and impose an equation of state [49, 55, 23, 22, 12, 13, 45]. We follow the weakly compressible formulation, with an equation of state of the form

$$P=P_0\left[{\left(\frac{\rho }{{\rho }_0}\right)}^{\gamma }-1\right],$$ (23)

where P₀, ρ₀ denote reference pressure and density, respectively, and γ is the polytropic constant. It is a common practice [23, 13] to select $P_0=K={\rho }_0{c}_0^2∕\gamma$, where c₀ is the artificial speed of sound and K is the compressibility modulus of the material. In order to limit density variations and prevent excessive spurious pressure waves [12], we choose γ = 1. Here, c₀ is chosen based on the desired Mach number, Ma, and the characteristic velocity of the problem U_c. For problems involving liquids, a typical choice is to use Ma = 0.1 to reduce compressibility effects, and thus c₀ = 10 U_c. For solids, previous works [44, 56, 45] have used the same formulation ($P_0={\rho }_0{c}_0^2∕\gamma$), in which the sound speed of the solid is computed using the shear modulus G and Poisson ratio of the material, ν_p, as $c_0=\sqrt{2G(1-{\nu }_p)∕{\rho }_0}$.

In addition, for solid particles, we suggest the addition of an artificial stress term to Eq. (18), as described by Monaghan [44], as we found that the transport-velocity formulation was not capable of removing the tensile instability in solids completely without introducing excessive particle distortion.

2.4. Defining the transport velocity

The transport-velocity formulation introduces the velocity of the reference frame, $\tilde{\mathit{v}}$, into Eqs. (6)-(8). This arbitrary velocity determines the nature of the reference frame, adjusting the conservation laws to an Eulerian, Lagrangian or any arbitrary mode in between these descriptions, therefore providing a arbitrary Lagrangian Eulerian (ALE) formalism to SPH [43].

We adopt the transport velocity correction term [22] as our arbitrary velocity, which has the form of a background pressure gradient

$$\tilde{\mathit{v}}(t+\Delta t)=\mathit{v}(t)+\Delta t\left(\frac{\tilde{d}\mathit{v}}{dt}-\frac{1}{\rho }\nabla P_b\right),$$ (24)

where the background pressure gradient is discretized as

$${\mathit{f}}_{\text{PB}}={\left(\frac{1}{\rho }\nabla P_b\right)}_i\approx P_b\sum _j\frac{m_j}{{\rho }_i^2}\nabla W_{ij}$$ (25)

and P_b is chosen as the reference pressure, P₀. This choice is justified by the additional benefit that this term acts as a self-relaxation mechanism [46] in the linear momentum equation by balancing the actual hydrodynamic pressure gradient ∇P/ρ term, therefore reducing the tension instability in the flow and greatly improving the overall accuracy of the method.

2.5. Switch correction for pressure and filter

For fluid flows subject to large Reynolds numbers or shear effects, it has been reported that the usage of the continuity equation, Eq. (17) may result in errors and spurious pressure waves that deteriorate the accuracy of the numerical solution [57, 45]. In order to overcome this issue, Adami et al. [12] proposed the computation of the density via interpolation, which conserves mass exactly. Although these two formulations are mathematically equivalent [49], it has been shown that the usage of the continuity equation within an ALE framework results in smoother density fields [43]. However, experiments reported by Sun et al. [58] have shown that the pressure can still attain negative values, causing instabilities and numerical cavitation.

We propose the solution of the continuity equation, along with the usage of a pressure switch to address the numerical cavitation problem, which filters negative pressures. Both the filter and the switch are used only for fluid particles, as negative pressures are required for compressive stress in solids. A similar procedure was proposed by Sun et al. [58]. This simple correction is based on the identity

$$\begin{gathered} \sum _j{m}_j\nabla W_{ij}\cdot \left(\frac{P_i}{{\rho }_i^2}+\frac{P_j}{{\rho }_j^2}\right)\mathbf{I}= \\ \sum _j{m}_j\nabla W_{ij}\cdot \left(\frac{P_j}{{\rho }_j^2}-\frac{P_i}{{\rho }_i^2}\right)\mathbf{I}+2\frac{P_i}{{\rho }_i^2}\sum _j{m}_j\nabla W_{ij}\cdot \mathbf{I} \end{gathered}$$ (26)

and proceeds by dropping the second sum in Eq. (26) if the pressure is negative, i.e.,

$${\left(\frac{1}{\rho }\nabla P\right)}_i=\{\begin{array}{cc}\sum _j{m}_j\nabla W_{ij}\cdot P_{ij}^{+}\mathbf{I},\hfill & \text{if}{P}_{ij}^{+}\ge 0\hfill \\ \sum _j{m}_j\nabla W_{ij}\cdot P_{ij}^{-}\mathbf{I},\hfill & \text{else},\hfill \end{array}\phantom{\}}$$ (27)

where the pairwise pressures $P_{ij}^{+}$ and $P_{ij}^{-}$ are computed as

$$P_{ij}^{+}=\left(\frac{P_j}{{\rho }_j^2}+\frac{P_i}{{\rho }_i^2}\right),$$ (28)

$$P_{ij}^{-}=\left(\frac{P_j}{{\rho }_j^2}-\frac{P_i}{{\rho }_i^2}\right).$$ (29)

Finally, in order to damp high-frequency pressure waves and improve energy conservation, we use a Shepard filter in the density field every N_f timesteps [59]

$${\rho }_i=\frac{{\sum }_j{m}_j{W}_{ij}}{{\sum }_j\frac{m_j}{{\rho }_j}{W}_{ij}},$$ (30)

where the optimal frequency for filtering, N_f = 20, as reported by Colagrossi and Landrini [57], was used.

2.6. Temporal integration

Following the practice of several authors [44, 60, 12], the integration of Eqs. (17)-(20) was performed using a modified velocity-Verlet scheme. For the density and concentration fields, we have adopted an explicit midpoint method. Specifically, considering v_i, x_i, ρ_i, C_i, S_i the unknowns of the system, and f_ρ, f_v, f_C, f_S the right-hand sides of Eqs. (17)-(20), respectively, the proposed numerical integration is given by

Step 1

1. Initial half-steps

$${\rho }^{n+1∕2}={\rho }^n+\frac{\Delta t}{2}{f}_{\rho }^{n-1∕2},$$ (31)

$${\mathit{v}}^{n+1∕2}={\mathit{v}}^n+\frac{\Delta t}{2}{\mathit{f}}_v^{n-1∕2},$$ (32)

$${\tilde{\mathit{v}}}^{n+1∕2}={\mathit{v}}^{n+1∕2}+\frac{\Delta t}{2}{\mathit{f}}_{\text{PB}}^{n-1∕2},$$ (33)

$$C^{n+1∕2}=C^n+\frac{\Delta t}{2}{f}_C^n,$$ (34)

$${\mathit{S}}^{n+1∕2}={\mathit{S}}^n+\frac{\Delta t}{2}{f}_{\mathit{S}}^n.$$ (35)

1. Position update

$${\mathit{x}}^{n+1}={\mathit{x}}^n+\Delta t{\tilde{\mathit{v}}}^{n+1∕2}.$$ (36)

Step 2

1. Final half-steps

$${\rho }^{n+1}={\rho }^n+\Delta t{f}_{\rho }^{n+1∕2},$$ (37)

$${\mathit{v}}^{n+1}={\mathit{v}}^{n+1∕2}+\frac{\Delta t}{2}{\mathit{f}}_v^{n+1∕2}$$ (38)

$$C^{n+1}=C^n+\Delta t{f}_C^{n+1∕2},$$ (39)

$${\mathit{S}}^{n+1}={\mathit{S}}^n+\Delta t{f}_{\mathit{S}}^{n+1∕2}.$$ (40)

Although the method has two steps, notice that it requires the evaluation of the particle forces only once per time step. A necessary condition for stability, given by the Courant-Friedrichs-Lewy condition based on the artificial speed of sound c₀, was used to estimate a suitable time step Δt for each simulation [13]

$$\Delta t\le C\text{min}\left(\frac{h}{c_0+\mid U_c\mid },\frac{h^2\rho }{\mu },\sqrt{\frac{h}{g}}\right),$$ (41)

where g is the gravity acceleration, and a Courant number C = 0.25 was adopted.

3. Wall treatment: boundary volume fraction method

We start by considering a particle of fluid i, located at a weighted averaged distance d from the wall. As depicted in Fig. 1, the region of influence around particle i, denoted by Ω, has radius h. The shaded region represents the solid wall. We denote the intersection of wall and region Ω by S.

Fig. 1.

Schematic showing the influence domain Ω around particle i, nearby wall and intersection between Ω and the wall, denoted by S.

We assume that the curvature of the wall, κ_wall, is far smaller than the curvature of Ω, κ_Ω. Following Li et al. [37], we assign to particle i an extra variable, denoted by ϕ. We define ϕ as the ratio between the volumes of regions S and Ω, i.e., the boundary volume fraction (BVF), given by

$$\varphi ≔\frac{V^S}{V^{\Omega }}.$$ (42)

Notice that, for d = 0, the particle i is located exactly at the wall, and thus ϕ = 0.5. This allows us to use the variable ϕ to act as an indicator function of how close a particle is from the solid wall. It is important to highlight that the boundary volume fraction interface cutoff of 0.5 makes sense only within a predictor-corrector temporal integration scheme, as the theoretical value of ϕ = 0.5 at the interface is never met due to numerical precision. Thus, the particle will have its trajectory corrected (in the corrector step) only when it reaches the wall (in the predictor step). Nevertheless, pairwise and viscous effects of the wall particles remain in effect within the cutoff of the kernel function adopted, as in other SPH methods.

Assuming that both the wall and the support domain Ω have sufficient particles, we can approximate the volumes of regions S and Ω in Eq. (42) using the SPH formalism

$$V_i^S=\sum _{j\in S}\frac{m_j}{{\rho }_j}{V}_j{W}_{ij}=\sum _{j\in S}{\left(\frac{m_j}{{\rho }_j}\right)}^2{W}_{ij},$$ (43)

$$V_i^{\Omega }=\sum _{j\in \Omega }\frac{m_j}{{\rho }_j}{V}_j{W}_{ij}=\sum _{j\in \Omega }{\left(\frac{m_j}{{\rho }_j}\right)}^2{W}_{ij},$$ (44)

where Ω is the total set of particles, and S the subset of solid particles. Thus, the BVF of particle i, ϕ_i, written in terms of SPH formalism is given by

$${\varphi }_i=\frac{{\sum }_{j\in S}{\left(\frac{m_j}{{\rho }_j}\right)}^2{W}_{ij}}{{\sum }_{j\in \Omega }{\left(\frac{m_j}{{\rho }_j}\right)}^2{W}_{ij}}.$$ (45)

Compared to the standard SPH algorithm, the only major modification regarding the wall treatment in the SPH-BVF method is that the numerical integration of Eqs. (1)-(3) now includes an additional constraint: the following correction is performed in the velocity field of particle i if ϕ_i ≥ 0.5, i.e., if particle i penetrates the wall, we correct the velocity of particle i by reassigning its velocity to the value calculated using the bounce-back equation proposed by Li et al. [37]

$${\mathit{v}}_i^{\text{corrected}}=2{\mathit{v}}_i^{\text{wall}}+\Delta t{\mathit{a}}_i^{\text{wall}}-{\mathit{v}}_i+2\max (0,{\mathit{v}}_i\cdot {\mathit{e}}_i^n){\mathit{e}}_i^n,$$ (46)

where eⁿ = n^ω/n^ω denotes the unit normal vector pointing outward from the wall boundary, Δt is the time step and v^wall, a^wall are the local velocity and acceleration of the boundary, respectively. This equation results from the collision of two particles of arbitrary masses as described in Lifshitz et al. [61] in the limit case where one particle possesses much greater mass (m₁ ⪢ m₂) so that the inertial effects on the larger particle are negligible compared to the smaller particle bouncing-back. Because the collision is considered elastic, the conservation of energy is preserved. The normal vector for particle i, ${\mathit{n}}_i^w$, is given by the gradient of ϕ_i:

$${\mathit{n}}_i^w=\frac{{\sum }_{j\in S}{\left(\frac{m_j}{{\rho }_j}\right)}^2\nabla W_{ij}}{{\sum }_{j\in \Omega }{\left(\frac{m_j}{{\rho }_j}\right)}^2{W}_{ij}}.$$ (47)

Li et al. [37] suggest the approximation of the local wall velocity and acceleration of moving boundaries, ${\mathit{v}}_i^{\text{wall}}$, ${\mathit{a}}_i^{\text{wall}}$ as the velocity of the nearest wall particle. To increase the accuracy of this approximation, we propose the usage of a kernel-interpolated velocity and acceleration of solid particles. Thus, for a fluid particle i, its neighbor solid moves with

$${\mathit{v}}_i^{\text{wall}}=\frac{{\sum }_{j\in S}{\mathit{v}}_j{\left(\frac{m_j}{{\rho }_j}\right)}^2{W}_{ij}}{{\sum }_{j\in S}{\left(\frac{m_j}{{\rho }_j}\right)}^2{W}_{ij}},$$ (48)

$${\mathit{a}}_i^{\text{wall}}=\frac{{\sum }_{j\in S}{\mathit{a}}_j{\left(\frac{m_j}{{\rho }_j}\right)}^2{W}_{ij}}{{\sum }_{j\in S}{\left(\frac{m_j}{{\rho }_j}\right)}^2{W}_{ij}},$$ (49)

where the summations in Eqs. (48)-(49) are over the solid wall particles in the support of particle i (S).

Algorithm 1 SPH-BVF method

$$\begin{array}{cc}\hfill & \mathrm{Input}:\text{Given initial positions},\text{velocities and con-}\hfill \\ \hfill & \text{centrations of species for all particles}i\text{at time}\hfill \\ \hfill & t:{\mathit{x}}_i,{\mathit{v}}_i,C_i,\text{and integration timestep}\Delta t.\hfill \\ \hfill & \mathrm{Output}:\text{Positions},\text{velocities and concentrations}\hfill \\ \hfill & \text{of species for all particles}i\text{at time}t+\Delta t.\hfill \\ \hfill & 1:\text{Find forces},\text{for all}i:\hfill \\ \hfill & 2:\mathbf{for}\text{all i}\mathbf{do}\hfill \\ \hfill & 3:\text{Compute SPH approximations},\text{Eqs.}(17)\text{-}\hfill \\ \hfill & (19).\hfill \\ \hfill & 4:\text{Compute}{\varphi }_i,\text{Eq.}(45).\hfill \\ \hfill & 5:\mathbf{end}\mathbf{for}\hfill \\ \hfill & 6:\text{Perform temporal integration},\text{for all}i:\hfill \\ \hfill & 7:\mathbf{for}\text{all i}\mathbf{do}\hfill \\ \hfill & 8:\mathbf{After}\text{the modified velocity-Verlet final in-}\hfill \\ \hfill & \text{tegration step}(\mathbf{Step}2),\text{perform}\text{BVF}\text{correc-}\hfill \\ \hfill & \text{tion:}\hfill \\ \hfill & 9:\mathbf{if}{\varphi }_i\ge 0.5\mathbf{then}\hfill \\ \hfill & 10:{\mathit{v}}_i\leftarrow 2{\mathit{v}}_i^{\text{wall}}+\Delta t{\mathit{a}}_i^{\text{wall}}-{\mathit{v}}_i+2\max (0,{\mathit{v}}_i\cdot \hfill \\ \hfill & {\mathit{e}}_i^n){\mathit{e}}_i^n\hfill \\ \hfill & 11:\mathbf{end}\mathbf{if}\hfill \\ \hfill & 12:\mathbf{end}\mathbf{for}\hfill \end{array}$$

Notice that the accuracy of the computation of the normal vector and the BVF is strictly dependent on having enough particles to accurately represent the walls. Thus, thin walls, regions of large curvature and large particle spacing among wall particles are some of the limitations of the BVF method. In practice, we have found that three layers of particles are typically enough to obtain accurate results, while slightly increasing the computational load of the method. However, the overall computational cost for the present method must have the same order of magnitude as standard SPH, since the only algorithmic addition in SPH-BVF is computing the normals and the additional BVF field ϕ_i in Eq. (47), which can be performed in parallel with the evaluation of the pairwise forces, with the advantage that fluid particle penetration is explicitly avoided. A review of the algorithm is provided in Algorithm 1.

3.1. Implementation

The SPH-BVF method summarized in Algorithm 1 was implemented in a stable version of the open-source Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [62] (v.22 Aug 2018). Originally developed as a molecular dynamics code, LAMMPS can also be used as a library to develop new particle-based methods. The code features an efficient particle neighbor search algorithm based on Verlet lists. Our source code, along with instructions to reproduce the validation cases and the motivation problem are available at the Github page: https://github.com/briandrawert/SPH-BVF/, under a GPL v2.0 license.

4. Validation

In this section we validate the SPH-BVF method using several canonical examples.

First, a Poiseuille flow simulation is used to validate and verify the convergence of the fluid flow solver and the BVF boundary conditions. In addition, the new method is tested for different kernels. In our second example we validate our method with the Taylor-Green vortex flow problem and compare the results with the standard SPH method, showing that the SPH-BVF method resolves the velocity decay accurately, without excessive diffusion. Next, a lid-driven cavity flow is used to validate the fluid flow solver and the BVF wall boundary conditions, which further validates our method over a wider range of Reynolds numbers and demonstrates that fluid particles do not penetrate through the walls. We validate the strong coupling of fluid flow and mass transport with a natural convection flow, emphasizing the elimination of tensile instabilities and particle alignments, and also demonstrating our method on curved walls. In our fifth example, we validate SPH-BVF for solid mechanics with an oscillating cantilever beam. This problem demonstrates the use of our method on a moving solid under tension, and further shows the elimination of tensile instability. Finally, we compare SPH-BVF with a finite element method using a fluid-structure interaction problem. This example also demonstrates our method in the context of sponge zones and flux boundary conditions.

4.1. Wall boundary condition validation: Poiseuille flow

We validate the proposed wall boundary condition method with a laminar, two dimensional Poiseuille flow in a closed channel as performed by Ferrand et al. [63]. The flow is driven by a constant volume force of magnitude 0.8 [ms⁻²], and periodic boundary conditions are imposed in the streamwise (x)-direction. The channel width is assumed to be W = 1 [m], where a fluid with viscosity ν = 10⁻¹ [m²s⁻¹] flows with a resulting Reynolds number Re = 10. We have considered five different particle refinements, with N_y = 20, 40, 80, 160 and 320 particles in the cross-stream (y)-direction. In addition to the standard Lucy kernel given by Eq. (10), we have performed convergence studies using the cubic spline kernel [44] and the Wendland quintic kernel [64]. In all cases, the kernel cutoff is set to h = 3Δp, which for a support of diameter 2h results in approximately 28 neighbors, and Δp is the particle spacing.

For a fully-developed, steady-state flow, the analytical velocity profile of the flow in the streamwise direction, $v_x^{\mathrm{a}}$, is given by

$$v_x^{\mathrm{a}}(y)=4Re\nu \frac{y}{W^2}\left(1-\frac{y}{W}\right),$$ (50)

Based on these levels of particle refinement, and using the analytical solution given by Eq. (50), we have performed a convergence study, taking as an error metric the L₂ norm of the global error [63, 65]

$$L_2\text{error}=\sqrt{\frac{1}{N_f}\sum _{i\in \text{fluid}}{\left(v_x^{\mathrm{a}}(y_i)-v_{x,i}^{\text{sph}}\right)}^2},$$ (51)

where N_f refers to the total number of fluid particles used in the L₂ error summation.

The errors obtained from the convergence study are provided in Table 1. The streamwise velocity profile of the flow is shown in Fig. 2-(a) for all the refinement levels. As reported in Ferrand et al. [63], we noticed that the error of the proposed BVF boundary condition has a non-constant slope, oscillating between first and second order convergence, as is observed under the Lennard-Jones and fictitious particles boundary conditions. This behavior is depicted in Fig. 2-(b). This result is expected because no kernel correction technique was enforced near the boundary, which also justifies the slower convergence behavior of the shear rate near the wall, as depicted in Fig. 2-(c). In terms of accuracy, the Lucy kernel performed better than both the cubic spline and Wendland kernels. We found the Wendland kernel produced more organized particles, but that did not translate into a higher convergence order. Thus, based on the superior accuracy and simplicity, we have opted to use the Lucy kernel hereafter.

Table 1.

Estimated errors and convergence rate of Poiseuille flow for different kernels.

Kernel	Ny	L2 Errora	Converg. rate, p630
Lucy	20	3.425 ×10−2	-
Lucy	40	6.598 ×10−3	2.376
Lucy	80	4.601 ×10−3	0.520
Lucy	160	1.505 ×10−3	1.612
Lucy	320	9.340 ×10−4	0.688
Cubic spline	20	2.169 ×10−2	-
Cubic spline	40	1.690 × 10−2	0.360
Cubic spline	80	9.512 ×10−3	0.828
Cubic spline	160	5.786 ×10−3	0.718
Cubic spline	320	6.620 ×10−4	−0.194
Wendland quintic	20	3.153 ×10−2	-
Wendland quintic	40	2.864 ×10−2	0.138
Wendland quintic	80	7.022 ×10−3	2.028
Wendland quintic	160	1.408 ×10−2	−1.003
Wendland quintic	320	1.206 ×10−2	0.223

^aError computed at steady-state, t = 100.

Fig. 2.

Results the SPH-BVF method and using Lucy kernel: (a) Streamwise profiles of a fully-developed, steady-state Poiseuille flow in a periodic channel, for N_y = 20, 40, 80, 160 and 320 particles in the cross-stream direction. (b) Convergence graph showing the L₂ error versus the refinement. (c) Comparison of shear rate in the lower part (0 ≤ y ≤ 0.5) of the channel.

4.2. Analytical solution validation: 2D Taylor-Green vortex

The Taylor-Green flow is a closed form solution of the incompressible Navier-Stokes equations, and is widely used to validate fluid flow solvers. It consists of the decaying of a vortex due to viscous effects of the fluid, and is given by the following analytical velocity fields [12]

$$v_x^{\mathrm{a}}(x^{\ast },y^{\ast },t^{\ast })=-U{e}^{b{t}^{\ast }}\cos (2\pi x^{\ast })\sin (2\pi y^{\ast }),$$ (52)

$$v_y^{\mathrm{a}}(x^{\ast },y^{\ast },t^{\ast })=U{e}^{b{t}^{\ast }}\sin (2\pi x^{\ast })\cos (2\pi y^{\ast }),$$ (53)

where b is the decay rate of the velocity field and U is the maximum initial velocity. We use Eqs. 52-53 to estimate the accuracy of the SPH-BVF method. In our simulations, we assume a Reynolds number Re = UL/ν = 100, a maximum velocity U = 1, a decay rate b = −8π²/Re and a domain of length L = 1. The boundary conditions are periodic in both directions, with x*, y* ∈ [0, 1] × [0, 1]. The initial conditions are obtained by setting the dimensionless time t* = tU/L = 0 in Eqs. 52-53. The unit length domain is discretized using three levels of equally-spaced particle refinements: N = 50², 100² and 200². For each simulation, the relative error of the numerical solution is measured over time using the L_∞ norm, given by

$$L_{\infty }(t^{\ast })=\mid \frac{{\max }_i(\Vert {\mathit{v}}_{\mathit{i}}(t^{\ast })\Vert )-U{e}^{b{t}^{\ast }}}{U{e}^{b{t}^{\ast }}}\mid .$$ (54)

Figure 3 shows snapshots of the particles at dimensionless times t* = 0.1, 0.5 for the case of N = 50². The top figures (a,b) show the results for the standard SPH, and the bottom figures (c,d) correspond to results from the present method (SPH-BVF). In (a,b), it is possible to visualize the anisotropic particle alignment caused by tensile instability. This alignment causes excessive diffusion, leading to a fast decay of the velocity field. In contrast, the results obtained by the SPH-BVF method (c,d) dramatically reduce the particle alignments and tensile instabilities, thus preserving the velocity decay. Remarkably, we found that the SPH-BVF method was able to prevent tensile instabilities even in the case of an initial regular lattice particle distribution. No significant differences were observed for other arrangements of particles (data not shown), including randomly shifted arrangements. Conversely, in the work of Adami et al. [12], it was found that the original transport-velocity formulation was sensitive to the initial particle distribution. We believe that our method does not suffer from this sensitivity, thus resulting in a more accurate velocity decay.

Fig. 3.

Contour plots of the norm of the velocity vector showing particle arrangements in 2D Taylor-Green vortex simulations at two time points: (a) Standard SPH, t* = 0.1, (b) Standard SPH, t* = 0.5, (c) SPH-BVF (present method), t* = 0.1, (d) SPH-BVF (present method), t* = 0.5.

The velocity decay is shown in Fig. 4. We compare our results with the exact solution Ue^bt* and plot the maximum velocity for all three particle refinements (N = 50², 100², 200²). Following [12], we also compare our method with standard SPH, showing that the latter fails to predict the exact decay. In contrast, the SPH-BVF method accurately predicts the decay, even for the coarser refinement (N = 50²). Compared to [12], the SPH-BVF method appears to not suffer from the shifted profile obtained by the original transport-velocity formulation.

Fig. 4.

Temporal evolution of the decay of the maximum velocity (semi-log scale) in 2D Taylor-Green vortex simulations for three particle refinements (N) that are compared to the exact analytical solution and standard SPH. Inset shows an expanded view of a section of the graph.

In addition to the velocity decay, the temporal evolution of the L_∞ norm, Eq. (51), is shown in Fig. 5. The relative error of the maximum velocity, L_∞, is ≈ 2% for all tested cases. This result is comparable to the best results obtained by [12] (non-regular initial particle distribution, N = 200²). Remarkably, the SPH-BVF method was able to achieve excellent results even at the lowest resolution (N = 50², equally spaced, regular lattice particle distribution).

Fig. 5.

Temporal evolution of the relative error of the maximum velocity (L_∞ norm) in the Taylor-Green simulations for three particle refinements (N).

4.3. Fluid mechanics validation: lid-driven cavity flow

The lid-driven cavity flow is a classical model problem, and is considered a challenging problem to be solved using SPH [22]. We validate the proposed method using the high-resolution finite difference numerical experiment carried out by Ghia et al. [66]. It consists of a square cavity of side L, filled with a Newtonian fluid of kinematic viscosity ν = μ/ρ. Gravity effects are considered negligible. In Fig. 6(a), the schematic of the lid-driven cavity flow is presented.

Fig. 6.

(a) Schematic of lid-driven cavity flow. Isocontours of velocity magnitude for (b) Re = 100, (c) Re = 1000 and (d) Re = 10000 at steady-state.

The flow, initially at rest, is induced by shear as the lid of the cavity starts moving at uniform velocity v₀. The governing equations are nondimensionalized, in order to validate our results with the reference. The dimensionless groups are given by

$$x_o=L,$$ (55)

$$t_o=x_o∕v_o,$$ (56)

$$P_o={\rho }_o{v}_o^2,$$ (57)

where ρ_o is a reference density, considered here as unity. Using these groups, Eqs. (1)-(3) are rewritten as

$$\frac{d{\rho }^{\ast }}{d{t}^{\ast }}=-{\rho }^{\ast }{\nabla }^{\ast }\cdot {\mathit{v}}^{\ast },$$ (58)

$$\frac{d{\mathit{v}}^{\ast }}{d{t}^{\ast }}=-{\nabla }^{\ast }{p}^{\ast }+\frac{1}{Re}{\nabla }^{\ast 2}{\mathit{v}}^{\ast },$$ (59)

where Re = v₀L/ν denotes the Reynolds number with respect to the characteristic length L. The walls of the cavity are modeled using three layers of fixed solid particles, so that near-wall fluid particles are guaranteed to have enough support for accurate ϕ_i computations.

To test the convergence of the method, simulations were performed using three levels of particle refinement (N = 50², 100², 200² particles) for each Reynolds regime (Re = 100, 1000, 10000), resulting in a total of nine simulations. In all cases, we have used the Lucy kernel, with cutoff h = 2.6Δp. We assumed that steady-state was reached once the total kinetic energy of the system was constant over time within a 10⁻³ tolerance.

An overview of the flow dynamics on the lid-driven cavity is provided in Figs 9(b)-(c), showing the isocontours of the flow velocity magnitude for each Reynolds flow regime using N = 200² particles. Figure 7 shows the vertical and horizontal velocity profiles for all three levels of particle refinement. For Re = 100, the method provides results comparable to the reference, even for the smallest particle refinement, N = 50². For Re = 1000, the SPH-BVF results converge to the reference values. Notice that for N = 200² particles, the results are very close to those of the reference, even though Ghia et al. [66] used a higher resolution (257² mesh). For Re = 10000, it is possible to infer the convergence to the reference solution as the refinement level increases. Nevertheless, as observed by Adami et al. [12], a deviation from the reference data is observed, which can be justified by the requirement of a higher refinement level and by the lack of turbulence modeling. For Re > 10000, the flow does not converge to a steady-state [66].

Fig. 9.

(a) Schematic of natural convection in a cylinder inside a square enclosure. (b) Isocontours of the dimensionless concentration field C for Ra = 10⁴, (c) Ra = 10⁵ and (d) Ra = 10⁶ at steady-state.

Fig. 7.

(a), (c) Vertical and (b), (d) horizontal velocity profiles for Re = 100, Re = 1000 and Re = 10000 compared with the reference results of Ghia et al. [66].

Figure 8 shows the streamlines in the cavity for Re = 1000, revealing the two main structures of the flow: the left and right corner vortices. In his work, Ghia et al. [66] reported approximated heights of 0.15 and 0.35 for the left and right corner vortices, respectively (c.f. Fig. 8). Similarly, the expected values for the widths are approximately 0.20 (left) and 0.30 (right). The sizes of the vortices obtained by our simulations agree with the reference, showing that the SPH-BVF method was able to accurately predict these vortices, therefore validating the wall boundary formulation.

Fig. 8.

Streamlines and patterns of the corner vortices in the cavity for Re = 1000, obtained with the SPH-BVF method.

4.4. Convective transport validation: natural convection

We validate the coupling of advection-diffusion using a coupling force, based on the Oberbeck-Boussinesq approximation [67], in the context of the transport-velocity formulation. To the authors’ best knowledge, this is the first time an ALE formulation of SPH has been used to simulate convection. A classical test case widely used in the literature is the natural convection over a cylinder immersed in a square cavity. A complete description of the problem is given in Fig. 9. The system consists of a square enclosure, filled with fluid at rest. The wall boundaries of the cavity and in the interface between the cylinder and the fluid are modeled with non-moving SPH particles to enforce the no-slip boundary condition. Initially, the fluid is free of solute, i.e., C(x, 0) = 0. At t > 0, the wall concentrations of solute in the circular cylinder and at the enclosure walls are set to C_C and C_E, respectively. Since C_E > C_C, mass transfer begins to occur, and the system is treated as a binary mixture. The solute diffuses in the fluid over time, leading to mass stratification.

The Oberbeck-Boussinesq approximation is used to describe the mass transport phenomena, such that a driven body force is proportional to the variation of concentration C, gravity acceleration g and coefficient of mass expansion β. In this case,the body force in Eq. 2 takes the form

$${\mathit{F}}_{\mathrm{B}}=g\beta \Delta C{\widehat{\mathit{e}}}_y,$$ (60)

where ΔC = C − C_ref, C_ref is a reference concentration and ${\widehat{\mathit{e}}}_y$ is the y-direction component of the standard Cartesian basis, (${\widehat{\mathit{e}}}_x$, ${\widehat{\mathit{e}}}_y$, ${\widehat{\mathit{e}}}_z$).

The problem was addressed in previous works as natural convection of heat [68, 69, 70, 71], and has been tested in many different geometries [69, 72, 73, 74]. In order to validate results with the work of Moukalled and Acharya [68], the equations are rendered dimensionless, using the reference groups proposed by Gray and Giorgini [67]

$$x_o=L,$$ (61)

$$v_o=\sqrt{g\beta L\Delta C},$$ (62)

$$t_o=x_o∕v_o,$$ (63)

$$\Delta C_o=C_C-C_E,$$ (64)

$$P_o={\rho }_o{v}_o^2,$$ (65)

where ρ_o is a reference density, considered here as unity. Using these groups, Eqs. (1)-(3) are rewritten as

$$\frac{d{\rho }^{\ast }}{d{t}^{\ast }}=-{\rho }^{\ast }{\nabla }^{\ast }\cdot {\mathit{v}}^{\ast },$$ (66)

$$\frac{d{\mathit{v}}^{\ast }}{d{t}^{\ast }}=-{\nabla }^{\ast }{P}^{\ast }+\sqrt{\frac{Sc}{Ra}}{\nabla }^{\ast 2}{\mathit{v}}^{\ast }+C^{\ast }{\widehat{\mathbf{e}}}_y,$$ (67)

$$\frac{d{C}^{\ast }}{d{t}^{\ast }}=\frac{1}{\sqrt{RaSc}}{\nabla }^{\ast 2}{C}^{\ast },$$ (68)

where Sc = ν/α and Ra = gβΔCL³/νκ denote the Schmidt and mass transfer Rayleigh numbers, respectively.

Simulations were performed for Ra = 10⁴, 10⁵ and 10⁶. The Schmidt number was taken to be equal to 0.7, and the cylinder diameter as D = 0.2L. For all the cases, the same number of particles N and same initial conditions were provided. The initial setup consists of N = 200² equally-spaced particles distributed in a squared domain of length L = 1. In all cases, we have used the Lucy kernel, with cutoff h = 2.6Δp. Boundary conditions are imposed using three layers of boundary particles in the walls. The cylinder at the center of the cavity is considered a boundary. Dirichlet boundary conditions are imposed by directly setting the concentration of boundary particles. As in the cavity flow, we assumed that steady-state was reached once the total kinetic energy of the system was constant over time within a 10⁻³ tolerance.

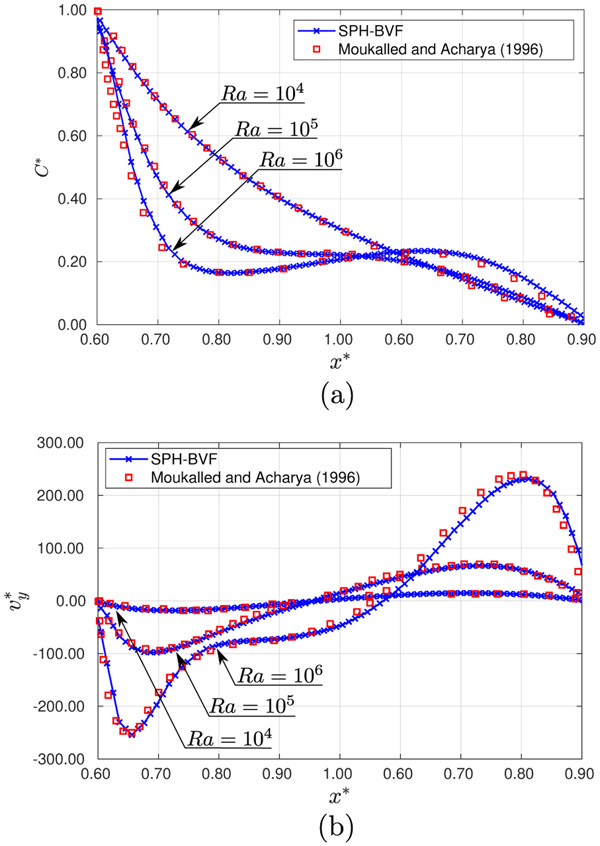
Profiles of the dimensionless concentration, C*, and y-velocity component, $v_y^{\ast }$, are shown in Figs. 10a-10b. Results were compared with the numerical simulation of Moukalled and Acharya [68]. Since Moukalled and Acharya [68] use a different normalization for the velocity, the dimensionless velocity v* obtained from the solution of Eq. (67) must be re-scaled, by multiplying v* by $\sqrt{Ra∕Sc}$.

Fig. 10.

(a) Profiles of dimensionless concentration C* and (b) y-velocity $v_y^{\ast }$ profiles along the horizontal centerline of the cavity, for Ra = 10⁴, 10⁵ and 10⁶, at steady-state.

As depicted in Figs. 10a-10b, satisfactory results were obtained for all of the Ra regimes. The method was also capable of capturing the stratification of the concentration profiles between the wall and the cylinder surface at Re = 10⁵ and the concentration inversion that occurs at Ra = 10⁶, which causes the flow to slow down in the interval 0.65 ≲ x* ≲ 0.85.

A comparison between the mean velocity fields obtained using the present method and standard SPH for Ra = 10⁶ is shown in Fig. 11. While the results obtained by the standard SPH method have serious particle voids, penetration in the walls and in the cylinder, clumping and alignments, the SPH-BVF method mitigated all of these problems, while improving stability. The time step required for a stable simulation with SPH-BVF ($\mathcal{O}({10}^{-4})$) was two orders of magnitude larger than the one required in practice using standard SPH, as the soundspeed must be increased to help mitigate the tension instability.

Fig. 11.

Comparison of mean velocity fields at time t* = 4, for the natural convection problem solved using (a) SPH-BVF method and (b) standard SPH [2] method, showing that the proposed method prevents particle penetration and mitigates tensile instability and anisotropic particle alignment.

4.5. Solid mechanics validation: oscillating cantilever beam

We validate the solid mechanics part of the method with the test case of an oscillating cantilever beam. The problem consists of a thin plate of length L and thickness H, fixed on one edge and free on the other edges, as shown in Fig. 12.

Fig. 12.

Schematic of the oscillating cantilever beam. The beam, initially at rest, is subject to the initial condition given by Eq. (70).

The plate, initially at rest, is set to oscillate at one of its fundamental modes, namely at kL = 1.875 [56]. For different modes, other wavenumbers k can be found using the eigensolutions of the Euler-Bernoulli beam equations, given by

$$\cos (kL)\cosh (kL)=-1.$$ (69)

For the mode kL = 1.875, the resulting initial velocity profile is perpendicular to the plate and is given by

$$v_y^0(x)=V_0{c}_0\frac{F(x)}{F(L)},$$ (70)

where V₀ is the magnitude of the velocity, c₀ is the soundspeed of the material and F is a force that varies along the length of the plate (x-direction)

$$\begin{gathered} F(x)=[\cos (kL)+\cosh (kL)][\cosh (kx)-\cos (kx)] \\ +[\sin (kL)-\sinh (kL)][\sinh (kx)-\sin (kx)]. \end{gathered}$$ (71)

In order to allow a direct comparison with the previous results of Zhang et al. [45], we set the plate properties using a Poisson ratio ν = 0.3975, density ρ = 1 × 10³[kg/m³] and Young’s modulus E = 2.0 × 10⁶[Pa]. We have performed simulations for initial velocity amplitudes V₀ = 1 × 10⁻³, 1 × 10⁻² and 3 × 10⁻²[m/s]. The artificial stress coefficient [44] is set to 0.2. In all cases, we have used the Lucy kernel, with cutoff h = 3.0Δp. The fixed support of the plate is constructed with stationary solid particles. For geometrical consistency, thickness of the upper and lower parts of the support were set to T = H/2.

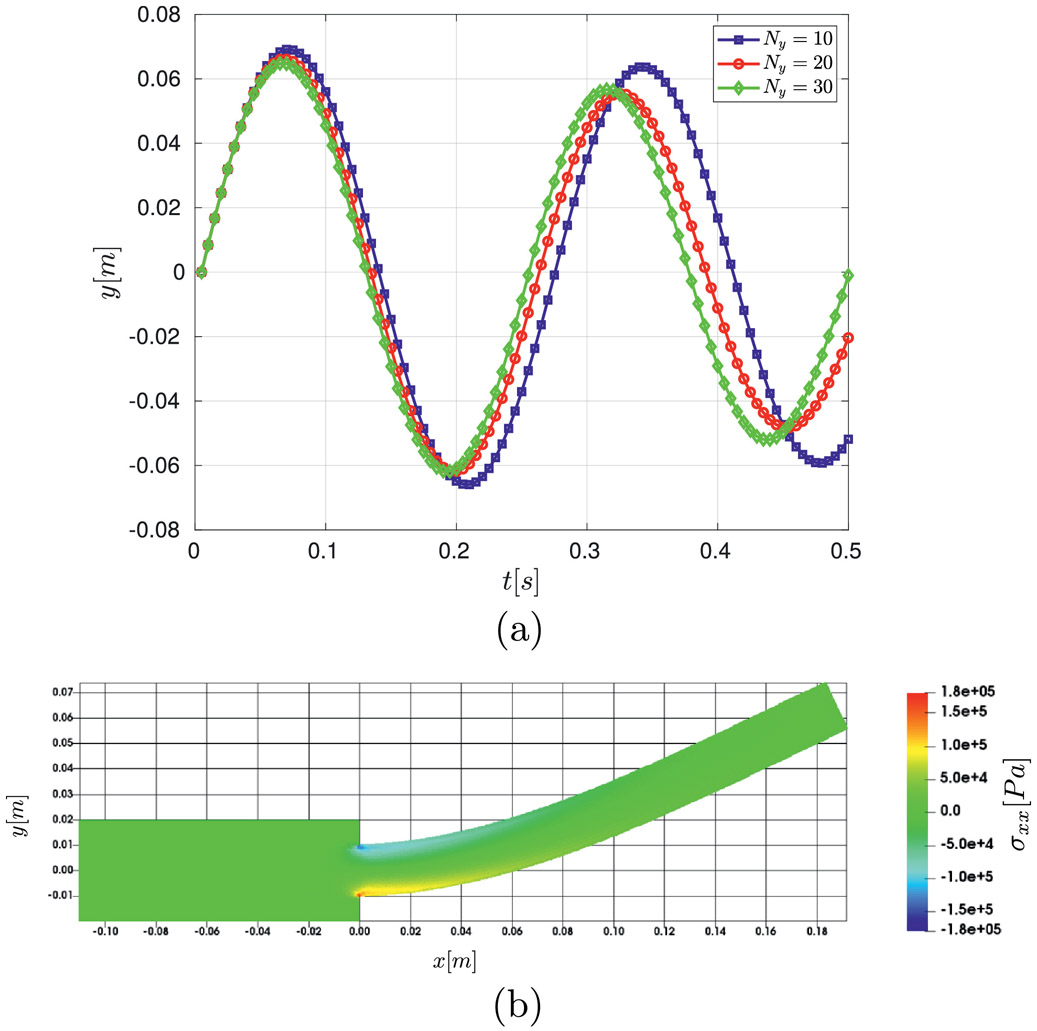
Figure 13-(a) shows a convergence study based on the y-position of the centerline point of the beam at the tip (x = L). Results are in good agreement with previous studies [56, 45], and no numerical fracture is observed in the regions of maximum tension, as shown in Figure 13-(b), demonstrating that the tension instability was controlled and allowed large deformations of the beam.

Fig. 13.

(a) Plots of the position of the centerline point at the tip of the beam (y = 0, x = L) for the case of V₀ = 3 × 10⁻², illustrating the convergence of the SPH solid mechanics formulation. (b) Contour plots of total stress field σ_xx at t = 0.07[s], for the case of V₀ = 3 × 10⁻² and N_y = 30.

A quantitative comparison with the analytical solution of a flat plate [61] for various velocity amplitudes V₀ and a relative error convergence analysis are shown in Table 2. The present method achieved relative errors of less than 1% for N_y = 30 and all values of V₀ compared to the 13% errors reported by Zhang et al. [45].

Table 2.

Relative errors for oscillating cantilever beam for various velocity amplitudes V₀ and particle refinements.

V0	Δp	Ny	First period (present work)	First period (analyticala)	Relative error (%)
1 ×10−3[m/s]	0.2/10[m]	10	2.747 ×10−1[s]	2.540 ×10−1[s]	8.150
1 ×10−3[m/s]	0.2/20[m]	20	2.605 ×10−1[s]	2.540 ×10−1[s]	2.559
1 ×10−3[m/s]	0.2/30[m]	30	2.539 ×10−1[s]	2.540 ×10−1[s]	−0.039
1 ×10−2[m/s]	0.2/10[m]	10	2.757 ×10−1[s]	2.540 ×10−1[s]	8.543
1 ×10−2[m/s]	0.2/20[m]	20	2.618 ×10−1[s]	2.540 ×10−1[s]	3.071
1 ×10−2[m/s]	0.2/30[m]	30	2.546 ×10−1[s]	2.540 ×10−1[s]	0.236
3 ×10−2[m/s]	0.2/10[m]	10	2.756 ×10−1[s]	2.540 ×10−1[s]	8.504
3 ×10−2[m/s]	0.2/20[m]	20	2.635 ×10−1[s]	2.540 ×10−1[s]	3.740
3 ×10−2[m/s]	0.2/20[m]	30	2.556 ×10−1[s]	2.540 ×10−1[s]	0.623

^aBased on Zhang et al. [45], Lifshitz et al. [61]

4.6. Comparison with FEM: fluid-structure interaction

As a final comparison, we demonstrate the ability of the SPH-BVF method to perform simulations of fluid-structure interaction (FSI) problems. The problem, depicted in Fig. 14, consists of a horizontal microchannel flow with a narrow vertical rod as an obstacle. A uniform fluid flow is introduced in the channel entry. In the region near the obstacle, the flow is induced into a narrow path in the upper part of the channel, and as a consequence it imposes a force on the structure’s walls. The rod, made of a deformable material, bends under the applied load, reaching a steady state.

Fig. 14.

Schematic of the FSI problem. Water enters in a 2D microchannel, filled with water at rest, with uniform velocity v_in. An elastic rod located at the middle of the channel and fixed at the lower wall, constraints the fluid flow, causing a deformation in the rod.

The wall boundary condition treatment in the SPH-BVF simulations follows the previous validation examples, with wall boundary conditions imposed using three layers of boundary particles in the walls. To model the inlet and outlet boundaries, we adopt the following strategy: as the fluid leaves the channel, it is re-inserted back at the inlet after it passes through a sponge zone, which acts as a non-reflective boundary condition [75] to the flow and re-align the velocity profile. This strategy makes the computation less intensive as there is no need to destruct particles as they leave the domain, or to create new ones at the inlet, as doing so would require re-creating the particle neighboring list every time step. For details on the implementation of the sponge zone, we refer the reader to Drawert et al. [76].

Since the problem has no analytic solution, we compare our numerical simulation with high-resolution FEM using the FSI package in Comsol Multiphysics (v.5.3). The physical parameters for both FEM and SPH-BVF simulations are given in Table 3.

Table 3.

Physical parameters adopted in the FSI simulation.

Parameter	Value	Description
Hchannel	100 [μm]	channel height
Lchannel	300 [μm]	channel width
Hrod	50 [μm]	rod height
Lrod	100 [μm]	horizonta position (rod)
δrod	5 [μm]	rod thickness
E	2 × 105 [Pa]	Young modulus (rod)
νp	0.33	Poisson ratio (rod)
ρf	1000 [kg/m3]	fluid density
ρrod	7850 [kg/m3]	rod density
μf	10−3 [Pa s]	viscosity of fluid
vin	3.33 × 10−2 [m/s]	inlet fluid velocity

The SPH-BVF simulation was performed using 30, 000 fluid particles (representing the water) and 500 solid particles (representing the rod). The FEM solution was obtained using second-order shape functions in a mesh of approximately 12,000 elements. We assumed that steady-state was reached once the kinetic energy of the fluid flow was constant over time within a 10⁻³ tolerance.

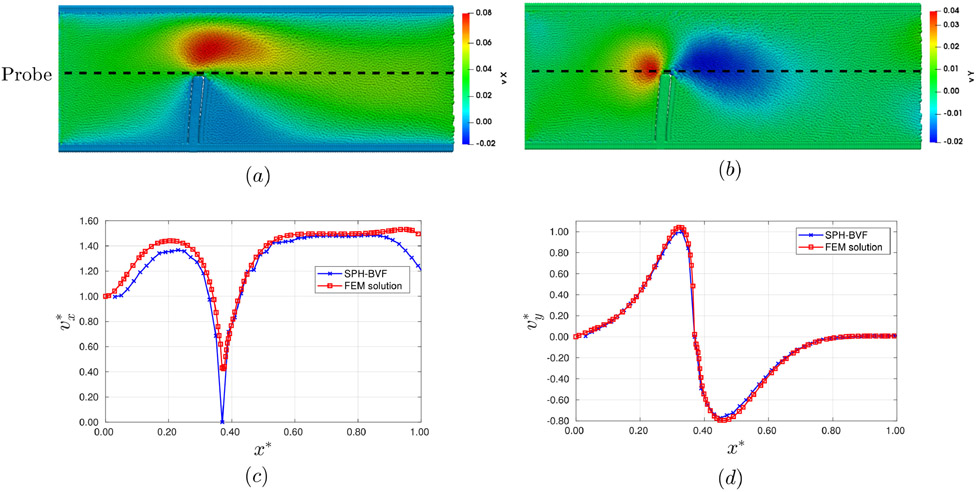
Contour plots of the streamwise (v_x) and cross-stream (v_y) velocity components at steady-state are shown in Figs. 15-(a) and (b). Is possible to see the bending of the beam to the right, as a consequence of the flow, as well as boundary layer in the near-wall regions of the channel. To validate the velocity profiles, a probe was placed along the y-centerline of the channel.

Fig. 15.

Top: contour plots of the (a) streamwise v_x and (b) cross-stream v_y velocity fields at steady-state. The beam has deformed slightly to the right. Bottom: comparison of dimensionless velocity profiles (c) $v_x^{\ast }$ and (d) $v_y^{\ast }$ for a probe located at the y-centerline of the channel, as depicted in the velocity profiles. Variables were rendered dimensionless for scaling purposes, as $v_x^{\ast }=v_x∕v_{\text{in}}$ and x* = x/L_channel.

Figures 15-(c) and (d) shows the velocity profiles of the channel at the probe, and a comparison with the FEM result. It is important to highlight that the comparison of velocity profiles in FEM and SPH-BVF agree in magnitude, demonstrating that the formulation for the non-reflexive boundary condition is satisfactory, as well as in phase, which demonstrates that the point of maximum deflection obtained in both FEM and SPH-BVF solutions are very close. However, notice that the stream-wise velocity v_x drops at the end of the channel, due to the presence of the sponge zone. Further investigations in non-reflective boundary conditions in SPH are required to improve these results.

5. Application: polarized yeast cell under-going mating projection growth

To further demonstrate the capability of the proposed method, we apply SPH-BVF to a biomechanics problem that poses a challenge for classic SPH as well as mesh-based methods because it involves deforming boundaries under pressure fluid-structure interaction, particle non-penetration and a conjugate transport mechanism (diffusion of chemical species that alters the mechanical properties of the material). The first attempt to simulate the mechanics of biological cells was performed by [77, 78], using an SPH-DEM hybrid method to study the mechanical response of plant cells under compression. The model, however, is purely mechanical, and therefore the reaction-diffusion dynamics of species in the cell wall are not considered.

The motivating problem is the growth of the mating projection in a yeast cell (S. cerevisiae) responding to mating pheromone in the extracellular fluid [79]. The key structure is the cell wall, which defines the shape of the cell while providing the mechanical integrity necessary to withstand the large internal turgor pressure [80]. As depicted in Fig. 16, under the isotropic turgor pressure, polarized growth occurs via localized softening of the cell wall by the enzymatic digestion of the polymer crosslinks, inducing expansion at the tip. A mechanical feedback pathway delivers new wall material to this growing region by vesicular transport leading to expansion of the mating projection at the area targeted by the wall-modifying enzyme [81]. This problem demonstrates our method on curved and dynamically changing boundaries representing the cell wall. Importantly, the interior fluid, the cytoplasm, does not penetrate the cell wall even while under sufficient pressure to cause the wall to change shape.

Fig. 16.

Schematic of yeast cell projection growth model. Cell wall modifying enzymes localized to region in red cause the softening of the cell wall. The internal turgor pressure pushes and deforms the cell wall at this weakened section, creating a mating projection. D is the diameter of the cell, H is the height of the enzyme region, and δ is the thickness of the cell wall.

5.1. Simplified model of yeast mating projection

Yeast mating projection growth is a classic example of cell polarization, and has been investigated experimentally [82, 83, 84] and through mathematical modeling [85, 86, 87]. Existing models have focused primarily on the reaction-diffusion dynamics of the signal transduction system. However, more recent work has highlighted the complex interplay between the biochemical dynamics within the mating projection and the mechanical forces acting on the cell wall to determine the shape of the cell [81]. It is important to note that the properties of biological materials involved are not well-characterized. For example, recent studies [88, 89] showed that cytoplasm can assume different properties, changing from a viscous fluid to an elastic solid, and can be considered compressible or incompressible, depending on the state of tension, biological process involved and external perturbations. Given that the SPH-BVF method is currently limited to linear elastic solids and Newtonian fluids, we assume that the cytoplasm is a compressible fluid, and that the cell wall is a linear elastic material characterized by a shear modulus. Finally, the extracellular fluid around the cell possesses the rheological properties of water.

For simplicity, we employ the following approximation of the coupling between the mechanical and biochemical systems. In the model, cell wall modifying enzymes, whose concentration is denoted by the variable c, decrease the shear modulus of the cell wall according to the following linear equation: G(c) = G₀(1 − cR), in which R is a parameter representing wall degrading enzymatic activity, and G₀ is the reference shear modulus of the non-polarized wall region. The modifying enzymes are able to diffuse in the wall with a diffusion constant given by κ_c.

Even under these simplifying assumptions, the model is still complex enough that advanced computer-aided engineering (CAE) tools have difficulty simulating the coupled problem. For example, COMSOL (v.5.3a) is not capable of simulating dynamic mechanical properties coupled with diffusive transport in a moving mesh, and hence no direct comparison could be made.

5.2. Results

To demonstrate that SPH-BVF can simulate yeast mating projection growth, we chose to vary the diffusion coefficient κ_c of the wall-modifying enzymes using two different values. The other parameters were kept constant with the enzyme initially distributed in a region of width H = δ/2, where δ is the cell wall thickness. The initial enzyme concentration was set to be c = 1 [mol/m³] in this region, and to c = 0 [mol/m³] in the rest of the cell wall. The enzyme affects the shear modulus of the cell wall according to the linear relationship described above as it diffuses from its initial site. A list of the physical parameters used in the simplified model is provided in Table 4, and a reference table with each case is detailed in Table 5.

Table 4.

Physical parameters used in the cell polarization simulation.

Parameter	Value	Description
δ	2.5 [μm]	cell wall thickness
D	10 [μm]	diameter of the cell
H	1.25 [μm]	height of enzyme region
E	106 [Pa]	Young modulus of cell wall
G0	3.58 × 105 [Pa]	reference shear modulus of cell wall
νp	0.3975	Poisson ratio of cell wall
Kf	5 × 105 [Pa]	bulk modulus of extracellular fluid
Kc	5 × 105 [Pa]	bulk modulus of cytoplasm
ρf	1000 [kg/m3]	density of extracellular fluid
ρc	1500 [kg/m3]	density of cytoplasm
ρw	1100 [kg/m3]	density of cell wall
μf	10−3 [Pa s]	dynamic viscosity of fluid
μc	10−3 [Pa s]	dynamic viscosity of cytoplasm
R	0.99[m3/mol]	rate of enzymatic softening

Table 5.

Two cases simulated with parameter values and number of particles.

Case number	Mass diffusivity (κc)	Number of particles (N)
I	10−13 [m2/s]	840 (wall), 716 (cytoplasm)
II	10−12 [m2/s]	840 (wall), 716 (cytoplasm)

Figure 17 shows snapshots of the two simulations (cases I and II) at the two diffusion values. Interestingly, the larger diffusion constant produced a longer, laterally concave projection, whereas the smaller diffusion constant preserved its laterally convex shape. One can compare the simulations to time-lapse microscopy images obtained by exposing yeast cells to the mating pheromone α-factor. The cells contain the secretion marker Fus1-GFP which indicates the presumptive location where the wall-modifying enzymes are deposited on the cell wall [90]. Qualitatively speaking, the simulations were able to capture the general shape changes during projection growth, even though some level of particle alignment is observed near the boundary of the cells. One promising way of alleviating this effect is to use an optimal particle arrangement [91], which directly ensures the isotropy of the particle distribution, even without parameter tuning. Regardless, this example demonstrates the potential of the SPH-BVF method to simulate complex biological processes including both biochemical and physical spatial dynamics, involving fluid-structure interactions and materials with time-varying mechanical properties without inducing particle penetration or excessive tension instability.

Fig. 17.

Simulations and experiments showing yeast mating projection growth over time. Cases I (left column, κ_c = 10⁻¹³ [m²/s]), II (right column, κ_c = 10⁻¹² [m²/s]), and microscopy images of a spa2Δ cell responding to 1 μM mating pheromone α-factor (central column). Particles are colored by the concentration c of wall-modifying enzymes. Rows A, B and C indicate times of 2000, 3000 and 4000 seconds, respectively, for the simulations, and 30, 60, and 90 minutes for the experiments. Cells contain the secretion marker protein Fus1-GFP (green) to indicate where wall-modifying enzymes are transported. A broad tip protrudes from both simulations and experiments. Despite high internal turgor pressure and deformation, SPH-BVF is able to model the deforming boundaries without particle penetration or tension instability. Scale bar = 2 μm.

6. Conclusion

We introduce a unified framework to simulate solid and fluid mechanics with convective reaction-diffusion transport in SPH. The method, named SPH-BVF, provides a new local wall boundary condition treatment for SPH, which allows particles to become autonomous to detect solid neighbors. The boundary volume fraction (BVF) approach introduces only a small computational overhead, while explicitly preventing fluid penetration through solid boundaries. In addition, SPH-BVF provides good accuracy and improved stability, and due to its ALE formulation, prevents tension instabilities and anisotropic particle alignments.

We have implemented our method within the LAMMPS [62] package. LAMMPS is a software package for simulation of classical molecular dynamics problems and is extensible to other particle-based methods. We have implemented the SPH-BVF method as a user module in LAMMPS. The complete code, along with all of the validations, post-processing routines and the application problem are also available in our source, under the GPL v2.0 license, which is the same license as the LAMMPS software package. For ease of replication of our results, we have packaged the solver and our examples as a Docker container https://hub.docker.com/r/briandrawert/sph_bvf/. Directions on how to use this container and the full source code are found on Github: https://github.com/briandrawert/SPH-BVF/.

While addressing some problems encountered by standard SPH, our method also possesses certain limitations. Simulations require approximately three layers of particles to have sufficient support within the kernel integration area to accurately estimate the boundary volume fraction. As a result, systems with very thin walls may require finer discretization and more particles, which can lead to higher computational costs. One promising approach to overcome this issue in the future is the usage of an immersed boundary method to represent slender bodies [92, 93]. We also note that the proposed BVF boundary condition has a non-constant order of convergence (between first and second order), which is similar to the Lennard-Jones boundary condition using ghost particles.

One promising domain for SPH-BVF is in simulating biophysical systems. Specifically, we envision its application in the modeling of cell dynamics, as well as in other applications, such as intercellular junction formation, cell morphogenesis and blood flow simulations in tissues coupled to inter- and intra-cellular processes, in which conjugate transport, materials with dynamic mechanical properties and boundary deformation are relevant.