Figure 1:

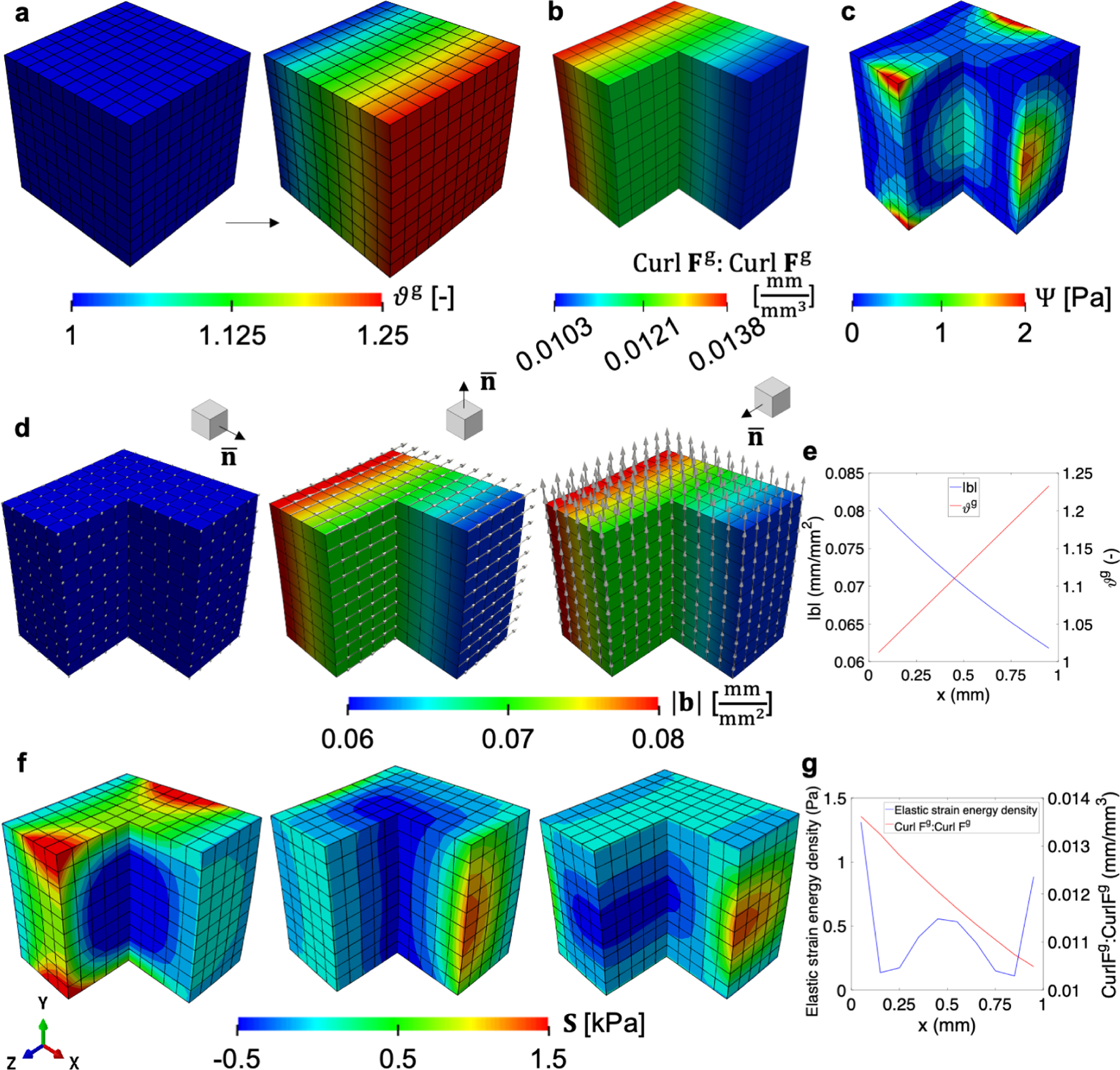
Isotropic growth guided by a unidirectional field. Finite element model of a simple cube deforms in response to a linear growth field, ϑ^g, with respect to the X₁ direction (a). Based on this growth field, the invariant of the incompatibility tensor Curl F^g : Curl F^g is obtained (b). There are only six constraints to prevent rigid body motion, but elastic free energy accumulates across the domain due to the incompatibility of the growth field (c). The local Burgers vector density b is derived with respect to the standard basis in 3D Euclidean space, $\overline{\mathbf{\text{n}}}\left(\text{d}\right)$. The arrows in (d) are scaled relative to the magnitude of |b|. For $\overline{\mathbf{\text{n}}}$ along the X₁ direction, there is no incompatibility. For the other two directions, b lies on the plane defined by $\overline{\mathbf{\text{n}}}$ and orthogonal to the growth direction. The magnitude of |b| shows an inverse trend compared to the growth value ϑ^g (e). The components of second Piola-Kirchhoff stress, S₃₃ and S₂₂, are matched with the local Burgers vector direction in (d) respectively when $\overline{\mathbf{\text{n}}}$ is not X₁ direction (second and third in f), while S₁₁ is plotted when there is no local Burgers vector (first in f). The free energy density and the invariant Curl F^g : Curl F^g are also plotted (g), showing that while incompatibility decreases along X₁, the strain energy is highest at the boundary, with another local maximum at the center of the domain.