Figure 3:

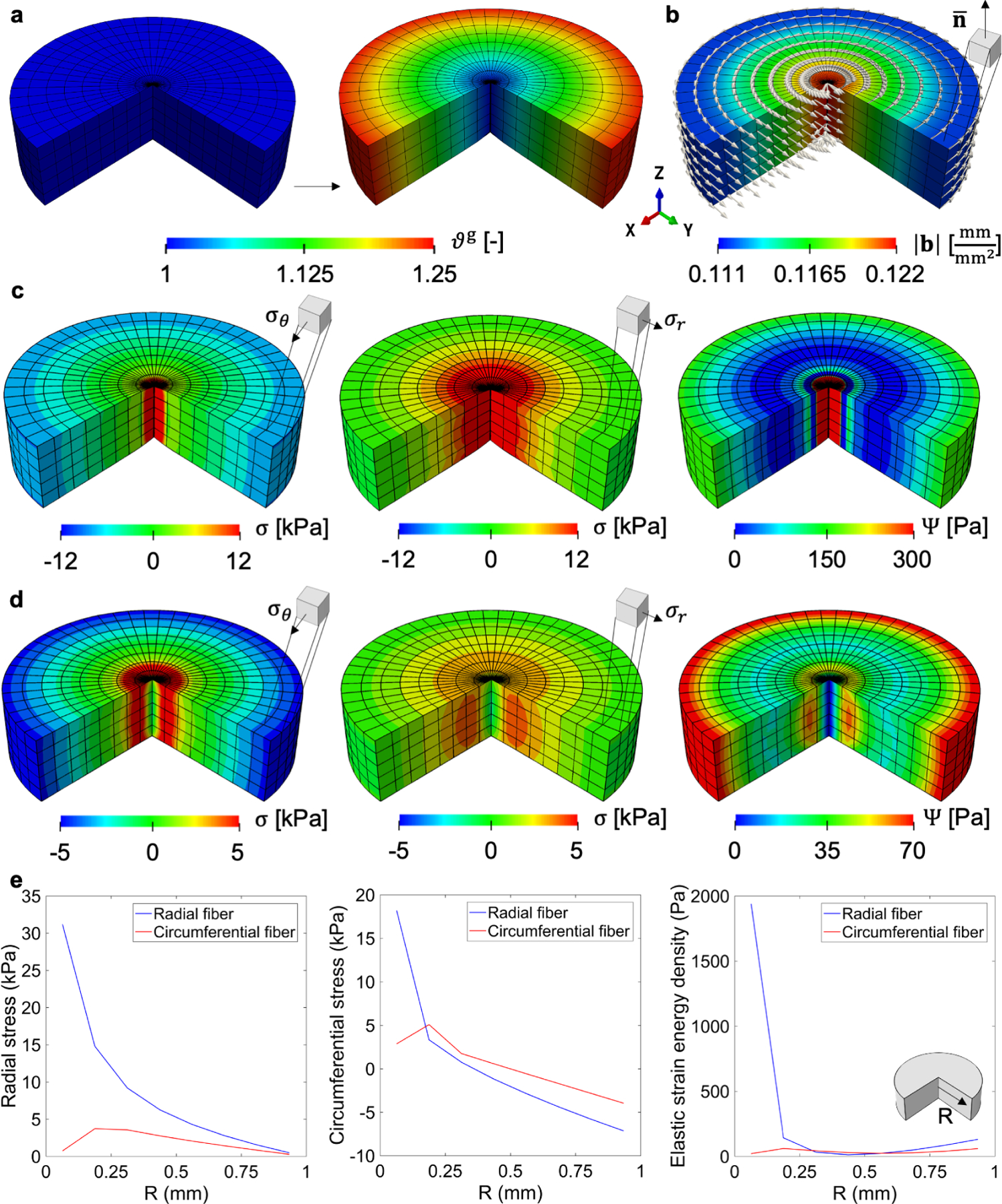
In-plane area growth: A flat disc grows in area driven by the linearly varying growth field ϑ^g along the radial direction (a). Even though the material is anisotropic, the amount of incompatibility is independent of the material behavior. The local Burgers vector density for the plane, defined by e₃ is aligned circumferentially (b). Residual stress, however, do depend on whether the direction of anisotropy is radial (c) or circumferential (d). The patterns in the elastic deformation are similar in both cases, with the circumferential component of the stress going from tension to compression from the center to the boundary of the disc. In contrast, the radial component of the stress has to satisfy a traction free boundary condition, and the stress decreases from the center to the periphery. Because the Gasser-Ogden-Holzapfel model leads to increasing stress when fibers are in tension, the overall stresses from radially aligned fibers are larger compared to circumferential fibers. Plots of σ_r, σ_θ, and Ψ with respect to R are shown in (e).