Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2021 Apr 23;6(17):11729–11739. doi: 10.1021/acsomega.1c01076

NanoTox: Development of a Parsimonious In Silico Model for Toxicity Assessment of Metal-Oxide Nanoparticles Using Physicochemical Features

Nilesh Anantha Subramanian †, Ashok Palaniappan ‡,*
PMCID: PMC8154018  PMID: 34056326

Abstract

graphic file with name ao1c01076_0009.jpg

Metal-oxide nanoparticles find widespread applications in mundane life today, and cost-effective evaluation of their cytotoxicity and ecotoxicity is essential for sustainable progress. Machine learning models use existing experimental data and learn quantitative feature–toxicity relationships to yield predictive models. In this work, we adopted a principled approach to this problem by formulating a novel feature space based on intrinsic and extrinsic physicochemical properties, including periodic table properties but exclusive of in vitro characteristics such as cell line, cell type, and assay method. An optimal hypothesis space was developed by applying variance inflation analysis to the correlation structure of the features. Consequent to a stratified train-test split, the training dataset was balanced for the toxic outcomes and a mapping was then achieved from the normalized feature space to the toxicity class using various hyperparameter-tuned machine learning models, namely, logistic regression, random forest, support vector machines, and neural networks. Evaluation on an unseen test set yielded >96% balanced accuracy for the random forest, and neural network with one-hidden-layer models. The obtained cytotoxicity models are parsimonious, with intelligible inputs, and an embedded applicability check. Interpretability investigations of the models identified the key predictor variables of metal-oxide nanoparticle cytotoxicity. Our models could be applied on new, untested oxides, using a majority-voting ensemble classifier, NanoTox, that incorporates the best of the above models. NanoTox is the first open-source nanotoxicology pipeline, freely available under the GNU General Public License (https://github.com/NanoTox).

Introduction

Nanotechnology has delivered the promise of “plenty of room at the bottom” with transformative applications for human welfare.1 The distinctive properties of nanoscale materials have been indispensable in industrial and medical applications, including the delivery of biologically active molecules and development of biosensors for human health and disease.2 Engineered metal-oxide nanoparticles are characterized by a concentration of sharp edges and lend themselves to a variety of uses (e.g., ref (3)). However, there is a potential caveat to nanobiotechnology: the differential nanoscale behavior of nanomaterials might also result in emergent toxic side effects in the biological domain and ecological realm.4−7 These hazards are related to the capacity of nanomaterials to engender free radicals in the cellular milieu, which inflict damaging oxidative stress. Such events could trigger inflammatory responses, which could balloon out of control, leading to apoptosis and cytotoxicity8−11 as well as genotoxicity.12

The mundane use of nanoparticles has necessitated vigorous safety assessment of toxicity, in the interests of sustainable progress.13−16 Such methods could also help discern safe-by-design principles that could guide adjustments to the nanoparticle formulation and thereby mitigate adverse effects at the source. Intelligent and alternative testing strategies could accelerate rational design of nanoparticles for optimal functionality and minimal toxicity.17−20 Various computational methods have been applied to predicting toxicity of engineered nanomaterials,21−31 but with the accumulation of high-quality data, machine learning methods have shown the most promise.32 Such techniques provide a noninvasive “instantaneous” readout of nanoparticle toxicity33−35 and originate from the evolution of quantitative structure–activity relationship (QSAR) models.36 Machine learning models of nanoparticle toxicity have tended to be either generalized37 or tissue-specific38,39 and are built from experimental toxicity data that have been scored, standardized, and curated into databases like the safe and sustainable nanotechnology db (S2NANO).40−42

Earlier studies have tended to neglect systematic multicollinearity among the predictor variables, which would lead to confounding and data snooping. Second, gross imbalance between the numbers of nontoxic and toxic instances usually exists, which could lead to overfitting to the “nontoxic” class.43 Third, we were motivated to develop a model that would be agnostic of in vitro characteristics, such as cell line, cell type, and assay method. A truly general model of nanoparticle cytotoxicity, independent of in vitro factors, would lead to significantly broader interpretability and wider applicability.44 Our study departs also from the notion that tissue-specific models are superior to generalized models39 and demonstrates that model interpretability is best achieved using a minimal nonredundant feature space, consistent with Occam’s parsimony. We have deployed insights from our study into a majority-voting ensemble classifier, with a view to increasing reliability. Finally, the end-to-end pipeline of our work, including the ensemble classifier, is made freely available as a user-friendly open-source nanosafety prediction system, NanoTox, under GNU GPL (https://github.com/NanoTox). All implementations were carried out in R (www.r-project.org).

Methods

Problem and Dataset

In vitro parameters such as cell type, cell line, cell origin, cell species, and type of assay could be extraneous to modeling the intrinsic hazard posed by a nanoparticle to cellular viability and the environment. This motivated us to formulate the problem in a feature space devoid of biological predictors. The machine learning task is stated as: given a certain nanoparticle at a certain dose for a certain duration, would its administration prove cytotoxic? To address this problem, we used a hybrid dataset building on the physicochemical descriptors and toxicity data found in Choi et al’s study.36 All in vitro features were removed from the dataset, as noted above. Extrinsic physicochemical properties, namely, dosage and exposure duration, were retained.45 The periodic table properties of metal-oxide nanoparticles published in Kar et al.46 were used to augment the dataset. Only complete cases were considered in the process of matching the two datasets. This process yielded a final dataset of 19 features of five metal-oxide nanoparticles: Al2O3, CuO, Fe2O3, TiO2, and ZnO (Table 1). Cytotoxicity was used as the outcome variable, encoded as “1” (true) if measured cell viability was <50% with respect to the control, and “0” (false) otherwise. The novel dataset is available on NanoTox.

Table 1. Physicochemical Features of MeOx Nanoparticles Considered in Our Study.

s no type of feature feature shorthand
1 intrinsic physicochemical properties core size CoreSize
2 hydrodynamic size HydroSize
3 surface charge SurfCharge
4 surface area SurfArea
5 conduction band energy Ec
6 valence band energy Ev
7 standard enthalpy of formation Hsf
8 Mulliken electronegativity MeO
9 enthalpy of formation of cation enthalpy
10 polarization ratio ratio
11 periodic table properties pauling electronegativity Eneg
12 summation of electronegativity esum
13 molecular weight MW
14 number of oxygen atoms NOxygen
15 number of metal atoms NMetal
16 ratio of esum to Noxygen esumbyo
17 oxidation state ox
18 extrinsic physicochemical properties exposure time Time
19 dosage Dose
Open in a new tab

Elimination of Multicollinearity

A nonredundant feature space would translate into an optimal hypothesis space. A simple inspection of the properties in Table 1 suggested the existence of correlated features. Correlated features would adversely impact model performance as well as complicate model interpretation. Multicollinearity is an even deeper problem in the pursuit of a nonredundant feature space.47 The training set alone was used for the feature selection process, to prevent any data leakage from the test set. The dataset was randomly split into a 70:30 train/test ratio stratified on the outcome variable.48 The existence of highly correlated (Pearson’s ρ ≥ 0.9) variables was ascertained. To address multicollinearity, we used a systematic variance inflation factor (vif) analysis. Each independent variable was regressed on all of the other independent variables in turn, and the goodness of fit of each of these models (fraction of variance explained; R2) was estimated. The vif score for each independent variable was then calculated using eq 1. In each iteration of the vif analysis, the variable in the current set that had the largest vif score when regressed on all of the other variables was eliminated. This process was continued until a set of variables all of whose vif scores <5.0 was obtained. Note that a vif score of 1.0 is possible only when a variable is perfectly independent of all other variables (all pairwise Pearson’s ρ identically zero).

graphic file with name ao1c01076_m001.jpg 1

Feature Transformation

The feature space could be vulnerable to heteroscedastic effects, given the varying scales for the variables. It is necessary to preprocess and prevent features with large variances from swamping out the rest. Positively skewed features could be stabilized using the log transformation. Ec values, which are negative, were first offset by +6.17, then log-transformed. Dosage spanned many orders of 10 and was log10-transformed. Exposure time spanned 2 orders of magnitude, so we performed a log2 transformation. Surface charge whose values could be either positive or negative was standardized (i.e., Z-transformed). All of the other features were log-transformed (to the base e).

Class Rebalancing

The cost of missing a toxic instance is manifold higher than the cost of missing a nontoxic instance, and the imbalance between toxic vs nontoxic instances could exacerbate this problem. In such situations, where the essential problem is to learn the minority outcome class effectively, resampling techniques could be useful.49 We addressed the class skew problem using Synthetic Minority Over-Sampling TEchnique (SMOTE).50 SMOTE synthesizes new minority samples from the existing ones, without influencing the instances of the majority class, thereby increasing the number of “toxic” instances relative to the number of nontoxic instances. Balancing the dataset thus would normalize the learning bias arising from unequal representation of the outcome classes.

Predictive Modeling

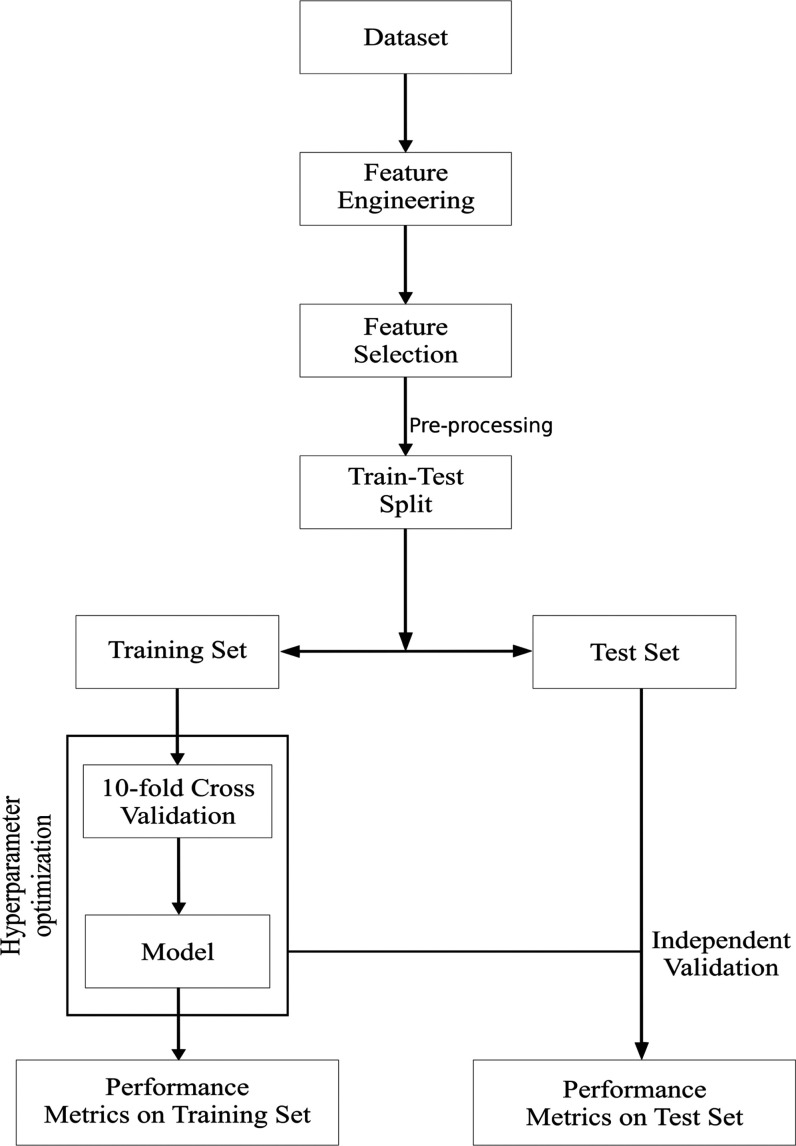
The overall workflow of our approach is summarized in Figure 1. The normalized training dataset was balanced using SMOTE, and a variety of classification algorithms were tried and tested, namely, logistic regression,51 random forests,52 SVMs,53 and neural networks.54,55Table 2 shows the classifiers and their hyperparameters considered in our work. The optimal values of the hyperparameters were found using 10-fold internal cross-validation.56 The performance of each optimized model was evaluated on the normalized and unseen test set. To penalize false positives and false negatives equally, we used an objective measure of performance

graphic file with name ao1c01076_m002.jpg 2

Figure 1.

Figure 1

Open in a new tab

Workflow of the study up to predictive modeling. Preprocessing refers to both normalization and class balancing. Only the training dataset was used for feature selection; the test set was kept invisible during the model development process.

Table 2. Classifiers Used in Our Study and Their Respective Hyperparametersa.

no. classifier type/Basis package/function hyperparameters optimization
1 logistic regression algebraic glm threshold (= 0.5) n/a
2 random forest rule-based randomForest 1 #trees (= 500) caret::train
2 mtry
3 support vector machine geometric e1071 1 Kernels (linear, radial, polynomial) e1071::tune
2 cost
3 γ
4 degree
4 neural networks connectionist RSNNS 1 #hidden layers = 1,2 caret::train, caret::mlpML
2 size of each hidden layer
3 decay rate
Open in a new tab
a

mtry represents the number of features used for each split in the random forest model.

Applicability Domain

The specification of the applicability boundaries of machine learning models would increase their reliability and utility.44 This would define the perimeter of model generalization to new instances and safeguard against application to atypical data. We used a Euclidean nearest-neighbor approach to define the applicability domain (AD) of the machine learning models.57 For each instance in the training set, its distances to all of the other training instances were found. The nearest neighbors of each instance are then defined as the k smallest values from this set, where k is an integer parameter set to the square root of the number of instances in the training set. The mean distance of an instance to its k-nearest neighbors is found, and this process is repeated for all instances to yield the sampling distribution of these mean distances. The mean and standard deviation of this sampling distribution were designated as μk and σk, respectively. The applicability domain is then defined as follows

graphic file with name ao1c01076_m003.jpg 3

where z is an empirical parameter (related to the z-distribution) that characterizes the width of belief in the model, which is here set to 1.96.

Results

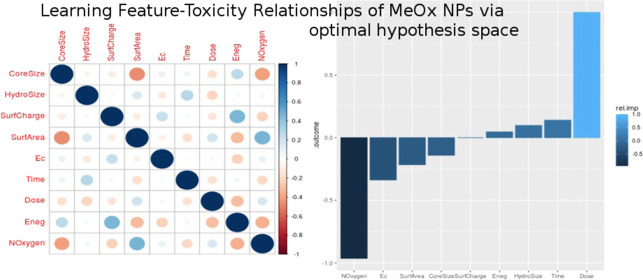
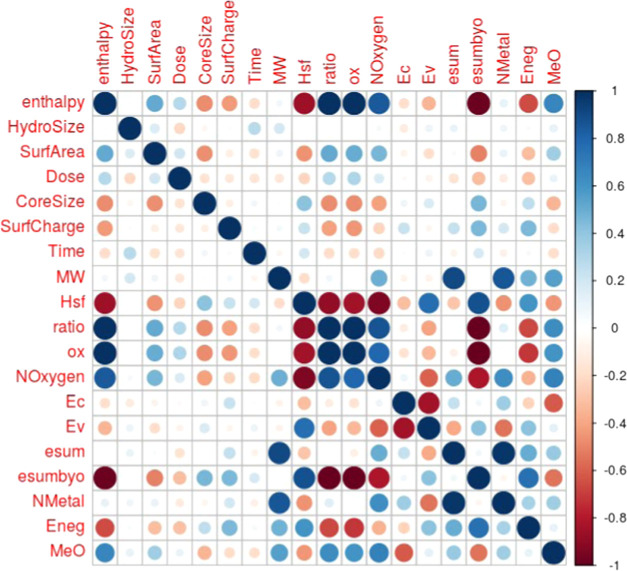
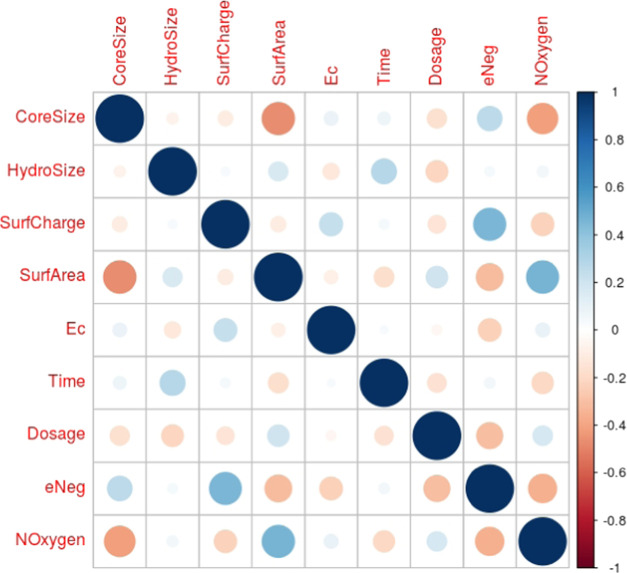
Our dataset consisted of 483 instances of the five metal-oxide nanoparticles with 19 features and one outcome variable. Correlogram plots identified the existence of high correlation among these 19 variables (Figure 2) and especially among the periodic table properties (Figure S1). Three clusters of high correlation were revealed: one cluster of enthalpy, Hsf, ratio, ox, Noxygen, and esumbyo; a second cluster of Ec and Ev; and a third cluster of esum, NMetal and MW. Based on the vif analysis, we were able to obtain a feature space of just nine uncorrelated nonredundant variables (Table 3). The highest vif of any variable in this feature space was <2.02, indicating little residual multicollinearity (Figure 3). This optimal feature space included two periodic table properties (Eneg, NOxygen), five other intrinsic physicochemical properties (CoreSize, HydroSize, SurfArea, SurfCharge, Ec), and both the extrinsic physicochemical properties (Dose, Time). This final dataset of 483 instances with nine features and one outcome variable is available at NanoTox.

Figure 2.

Figure 2

Open in a new tab

Correlogram of the 19 features. The correlation between a row feature and a column feature is shown by a dot in the corresponding cell. The size of the dot represents the magnitude of the correlation, and color represents the sign of the correlation—blue: positive; red: negative. White indicates a value near 0, i.e., independence.

Table 3. Vif Scores for the Features in the Final Reduced Seta.

s. no. feature variance inflation factor
1 CoreSize 1.65
2 HydroSize 1.24
3 SurfCharge 1.85
4 SurfArea 1.58
5 Ec 1.50
6 time 1.19
7 dose 1.21
8 Eneg 2.02
9 NOxygen 1.60
Open in a new tab
a

The maximum vif score is ∼2.0, corresponding to maximum R2 ∼ 0.5 (cf. eq 1).

Figure 3.

Figure 3

Open in a new tab

Optimal hypothesis space. A correlogram of the optimized feature space shows that no subset of variables in this set would yield multicollinearity.

The nine features were normalized, producing acceptable skew values for HydroSize, SurfArea, Ec, and Time (Table 4). The normalized dataset was partitioned using a random 70:30 split stratified on the outcome variable, providing a training dataset of 339 instances (with 55 toxic instances), and an independent test dataset of 144 instances (with 23 toxic instances). The training dataset (and not the test dataset) was balanced for the minority toxic instances using SMOTE resampling, yielding 165 toxic and 220 nontoxic instances, for a training dataset of 385 instances. This normalized and balanced dataset was used to train the various classifiers. The optimal hyperparameters of each classifier were determined using the R e1071 package for SVMs (Figure S2), and the R caret package for the neural networks, both one layer (Figure 4) and two layers (Figure S3). The full set of model-wise optimal hyperparameters could be found in Table S1. The trained, optimized classifiers were then evaluated on the unseen test dataset. All of the models, except the SVM with polynomial kernel, achieved perfect sensitivity to the toxic instances, i.e., all cytotoxic nanoparticles were classified correctly. The models were not perfectly specific to the nontoxic instances, however. On this count, the random forest and neural network one-layer models outperformed all of the others. They were each frustrated by eight false positives, resulting in a balanced accuracy of 96.69%. Bootstrapping the test set 500 times yielded standard errors of ∼0.0189 for both the random forest and neural network one-layer models, indicating performance robustness. All of the classifiers achieved balanced accuracy >90%. Table 5 summarizes the performance of all of the models on the test set. Five nontoxic instances were classified incorrectly by all of the models, representing refractory instances and constituting a challenge to perfect learning. One of these instances was only marginally viable (0.52), indicating the possible source of refractoriness.

Table 4. Dataset Normalizationa.

features skewness before type of normalization skewness after range (min–max)
CoreSize 0.92 log –0.2 2.01–4.82
HydroSize 1.76 log 0.14 4.30–7.52
SurfCharge 0.45 z-score 0.45 –1.62 to +1.98
SurfArea 2.14 log –0.23 1.95–5.35
Ec 2.68 log, with offset –0.23 0.00–1.54
Time 1.36 rescale, log –0.48 0.00–4.58
Dosage 1.74 log10 –1.5 –5.00 to +2.48
Eneg 1.46 log 1.26 0.43–0.64
Noxygen 0.66 none 0.66 1–3
Open in a new tab
a

Log-transformation was performed to the base e. Skewness was controlled, and the range of all predictors was brought into the same order of magnitude.

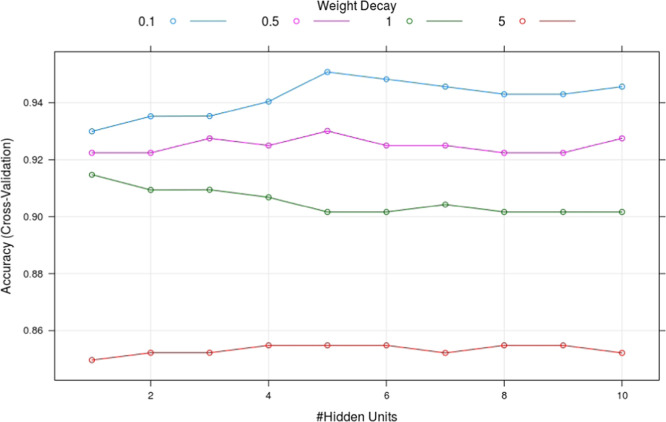
Figure 4.

Figure 4

Open in a new tab

Hyperparameter tuning, for the neural network—1 layer model. It is seen that the cross-validation accuracy is sensitive to the choice of the set of hyperparameters.

Table 5. Performance of the Various Modelsa.

    train set
 test set
id classifier accuracy balanced accuracy cross-valid accuracy accuracy balanced accuracy
model_1 logistic regression 0.94 0.94 0.93 0.91 0.95
model_2 random forest 0.98 0.98 0.94 0.94 0.97
model_3a SVM-Linear 0.94 0.95 1 0.9 0.94
model_3b SVM-Radial 0.94 0.94 1 0.86 0.92
model_3c SVM-Poly 0.98 0.98 1 0.84 0.85
model_4a neural network—1L 0.96 0.96 0.94 0.94 0.97
model_4b neural network—2L 0.96 0.95 0.95 0.91 0.95
Open in a new tab
a

Models with balanced accuracy >94% are highlighted.

Deployment

The applicability domain was calculated with the normalized train data, prior to SMOTE balancing. Substituting k = 19 and z = 1.96 in eq 2 yielded the AD threshold = 2.23. About 95% of the test instances (i.e., 137/144 instances) were located within the AD radius. It must be noted that the misclassified instances did not coincide with these outliers. We have provided a workflow, deployment.R (available at NanoTox), for prediction on new, untested oxides. The prediction is executed by a majority-voting ensemble classifier,58 since bagging the predictions of the best models on the test set improved the performance to just five false positives (∼98% balanced accuracy). Any new instance for classification supplied by the user is preprocessed (normalized), and its “typicality” is determined by calculating its distances to the instances in the original train data and finding the mean, Di, of the 19 closest distances. If Di is greater than the AD threshold, then the instance is deemed atypical for requesting the ensemble model. Predictions are obtained using the top two models, the random forest and the neural network one layer, and a consensus prediction is sought. In the absence of a consensus, an ensemble of the top five classifiers, all with balanced accuracy >94% (highlighted in Table 5), is used. In the end, the majority prediction of the ensemble classifier is the predicted cytotoxicity of the given instance. Deployment.R automates this pipeline for a batch of new, untested oxides of any size. Furthermore, the RDS images of all of the models trained in our study are provided on NanoTox, for the interested scientist.

Discussion

The results are encouraging since the test set constitutes an independent validation dataset. It is clear that SMOTE balancing made a difference in the ability of the classifiers to detect the under-represented toxic instances. Filtering based on applicability domain and use of an ensemble classification strategy further mitigate model uncertainty given the ‘no free lunch’ theorem.59 Benchmarking our results with Choi et al.,37 we see that the best model in each classifier from our work outperformed the corresponding best models of their work (Table 6). The overall best models in our work (random forest and neural network one layer) yielded a balanced accuracy of ∼97% compared to 93% for their best overall model (“neural networks”). All of the five models from this work with balanced accuracy >93% are deployed in an ensemble classifier to further mitigate uncertainty in prediction.

Table 6. Benchmarkinga.

  balanced accuracy (%)
model Choi et al.b present work
logistic regression 92 94.63
random forest 91 96.69
SVM 91 (a) 94.21
(b) 91.74
(c) 85.21
neural networks 93 (a) 96.69
(b) 94.63
Open in a new tab
a

SVM (a), (b), and (c) correspond to linear, radial, and polynomial kernels. Neural networks (a) and (b) refer to one and two hidden layer(s), respectively. No information regarding model hyperparameters were available in Choi et al. The best-performing models from our work are highlighted.

b

Ref (37).

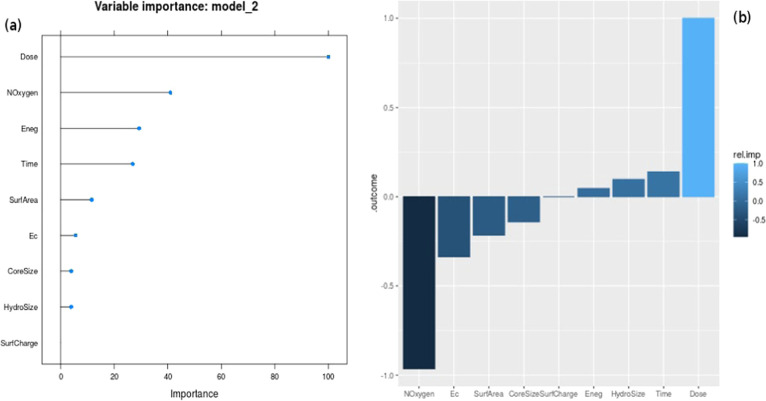
Measures of variable importance are central to mechanistic insights.60 Variable importance was assessed using the varImp caret function for the logistic regression model (Figure S4a), neural network one-layer model (Figure S4b), and random network model (Figure 5a). Dose emerges as the consensus key attribute for prediction; however, there are subtle ranking differences among the different models. NOxygen is a key attribute in both the random forest and neural network one-layer models, but not so for the logistic regression model. Time emerges as another consensus key attribute in all of the models. Logistic regression provides us with not only the effect size (coefficients) of the individual variables but also an estimate of their significance, in terms of the p-value of the coefficients (Table S2). The sign of the coefficient of each variable indicates the class outcome to which the respective variable contributes. It is notable that the two periodic table properties (Eneg, Noxygen) and the quantum chemical property, Ec, show large effect sizes but poor significance, while all of the other variables remain highly significant. Relative importance plots of the neural network models add a direction representing the favored binary outcome61,62 and obtain concurrence to these findings (Figures 5b and S5). Dose emerges as the key variable determining nanoparticle toxicity, and Time, HydroSize, and Eneg are the other variables influencing the toxic prediction. NOxygen emerges as the key predictor influencing the nontoxic prediction, and SurfArea, Ec, and CoreSize are the other predictors in this category. The numeric variable importance scores are given in Tables S3 and S4.

Figure 5.

Figure 5

Open in a new tab

(a) Normalized variable importance for the Random Forest model computed with caret. Dose is by and far the attribute with the greatest effect on the toxicity in the Random Forest model. (b) Relative importance plot for the NeuralNet-1L. Positive values correspond to the “true” (i.e., toxic) class, and negative values correspond to the nontoxic class. It is seen that Dose and NOxygen exert the maximum importance on the outcome class, though in opposite directions.

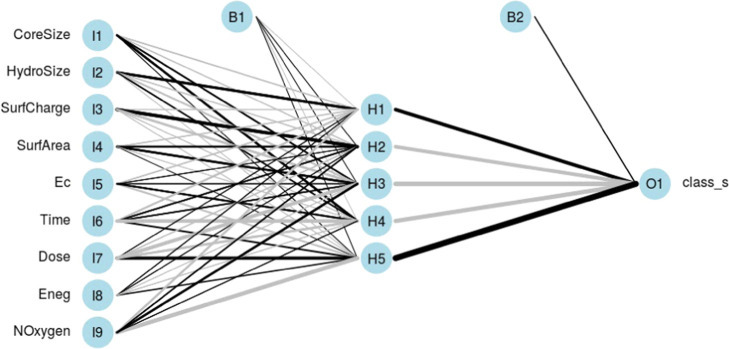
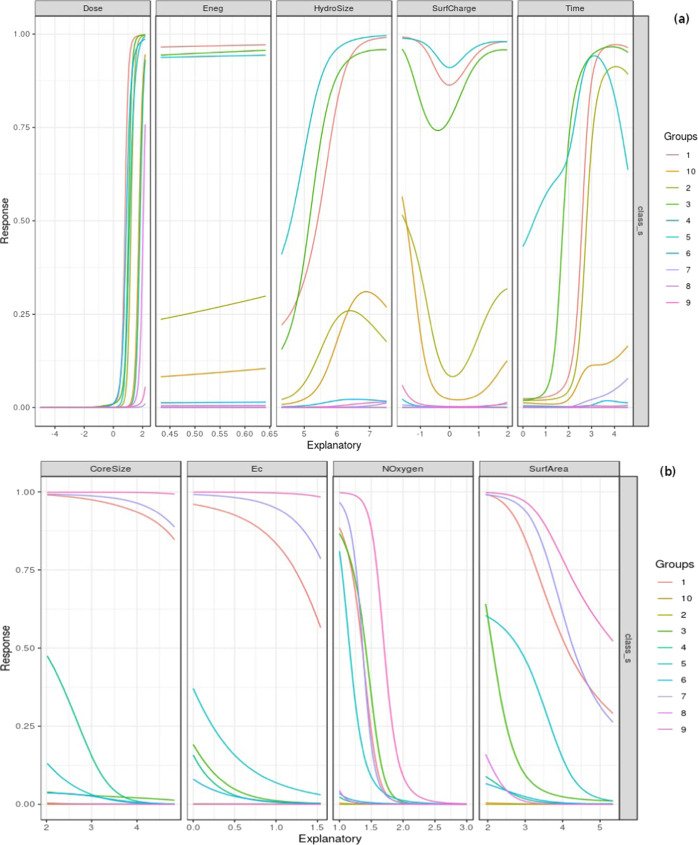
NeuralNetTools was used to visualize the best-performing one-layer neural network model, with the individual connections weighted by their importance63 (Figure 6). The two-layer neural network model was also visualized (Figure S6). Consensus among the models is necessary for explainable AI,64 and in this direction, we performed a Lek sensitivity analysis with the neural network one-layer model.65 How does the response variable change with changes in a given explanatory variable, given the context of the other explanatory variables? On investigating the effect of one explanatory variable, all of the other explanatory variables are clustered into a specified number of lakes with like members. While the unevaluated explanatory variables are held constant at the centroid of one lake cluster, the explanatory variable of interest is sequenced from minimum to maximum in 100 quantile steps, with the response variable predicted at each step, yielding a sensitivity curve. This process is iterated for each lake of the unevaluated explanatory variables, yielding the sensitivity profile of the response variable with respect to the specific explanatory variable in the context of the unevaluated explanatory variables. We set the number of clusters to 10, to visualize a sufficient number of response curves for each explanatory variable. In this way, the sensitivity profiles of the response variable are obtained for each predictor (Figure 7).

Figure 6.

Figure 6

Open in a new tab

Schematic of the trained neural network one-layer model, with the weights of the connections indicated by the linewidth. Black lines indicate positive weights, and gray lines indicate negative weights. Two bias units are seen, one for the hidden layer and the other for the output layer.

Figure 7.

Figure 7

Open in a new tab

(a) Lek sensitivity analysis of attributes with positive effect on the outcome class. The steep effect of Dose is evident, with the location of the tipping point moving slightly with the cluster of the unevaluated variables. Increasing exposure times and HydroSize are also seen to tip to toxicity. (b) Lek sensitivity analysis of attributes with relatively consistent negative effect on the outcome class: CoreSize, Ec, NOxygen, and SurfArea. The number of lakes of the unevaluated variables is set to 10 in both the cases.

The two input variables that decisively differentiate the outcome are Dose and Noxygen. Dose appears to exert a nearly thresholding effect on the toxic class. The consistent sigmoidal effect seen in the “dose–response” curve, independent of the lake of unevaluated explanatory variables, echoes the maxim attributed to Paracelsus, “The dose makes a thing poison.” The attributes influencing toxicity also included: (i) Time, with a pronounced effect depending on the lakes of the unevaluated variables; and (ii) HydroSize, with a steady nonlinear effect on toxicity that is also sensitive to the context of the unevaluated explanatory variables. The response profile for Eneg is almost flat at all lakes, indicating little to no effect in changing the outcome. The interpretation of the response with respect to SurfCharge remained obscure. NOxygen emerged as the attribute with the clearest inverse effect on toxicity, with a response profile displaying a tipping point to nontoxic class at most, but not all, of the centroids. Other attributes seen to dial down the toxicity include SurfArea, CoreSize, and Ec. These observations of effect size may be tempered with significance analysis toward a complete understanding.

In summary, the ML models of our work are represented by a purely numeric feature space of just nine predictors, and it is possible to consider them in their entirety, similar to the interpretability of a classical QSAR model. The models conform to the Findable, Accessible, Interoperable, Reusable (FAIR) principles and are presented in a unified ensemble prediction engine, NanoTox (https://github.com/NanoTox). In the interest of reproducible research, all the scripts necessary to replicate, apply, and extend our analysis are available at NanoTox. Our methods may be extendable to other classes of engineered nanomaterials requiring urgent, sustainable, and rapid hazard estimation prior to induction in practical uses.66−69

Conclusions

We have optimized the problem formulation of cytotoxicity modeling of nanoparticles using a principled approach agnostic of in vitro characteristics. The feature space is trimmed for multicollinearity, tunable hyperparameters were optimized, and the training data were corrected for class imbalance. These steps led to an optimal hypothesis space, thereby improving the performance of the generated ML models to >96% balanced accuracy. The benefits of a parsimonious approach to modeling nanoparticle toxicity include enhanced model interpretability and generalizability. We have embedded our models into an unambiguous ensemble classifier that surpasses ∼98% balanced accuracy. Our entire workflow is available as a free open-source resource for use and enhancement by the scientific community toward proactive noninvasive testing and design of nanoparticles for varied applications.

Acknowledgments

The authors thank the School of Chemical and BioTechnology, SASTRA Deemed University, for infrastructure and computing support. They thank Mani Narayanan for helpful discussions. This work was supported in part by the DST-SERB grant EMR/2017/000470/BBM and the SASTRA T.R.R. grant (to A.P.).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c01076.

  • Correlogram of periodic table descriptors (Figure S1); hyperparameter optimization of the SVM (Figure S2); hyperparameter optimization of the neural network two layer (Figure S3); hyperparameter optimization for the models in our study (Table S1); variable importance plots using the varimp function of the R caret package (Figure S4); summary of the logistic regression model (Table S2); relative importance plots of the neural network two-layer model using NeuralNetTools (Figure S5); Garson importance analysis of the neural network one-layer model (Table S3); relative importance analysis of the neural network two-layer model (Table S4); and schematic of the trained neural network two-layer model (Figure S6) (PDF)

Author Present Address

§ Department of Computer Science and Engineering, Indian Institute of Technology Madras, IIT P.O., Chennai 600036, India.

Author Contributions

A.P. conceived and designed the work. N.A.S. and A.P. performed research and analyzed the results. A.P. wrote the paper.

The authors declare no competing financial interest.

Supplementary Material

ao1c01076_si_001.pdf (400.5KB, pdf)

References

  1. Sanvicens N.; Marco M. P. Multifunctional nanoparticles–properties and prospects for their use in human medicine. Trends Biotechnol. 2008, 26, 425–433. 10.1016/j.tibtech.2008.04.005. [DOI] [PubMed] [Google Scholar]
  2. Functional Metal Oxides: New Science and Novel Applications; Ogale S. B.; Venkatesan V. T.; Blamire M., Eds.; John Wiley & Sons, 2013; pp 1–498. [Google Scholar]
  3. Subbiah D. K.; Babu K. J.; Das A.; Rayappan J. B. B. NiOx Nanoflower Modified Cotton Fabric for UV Filter and Gas Sensing Applications. ACS Appl. Mater. Interfaces 2019, 11, 20045–20055. 10.1021/acsami.9b04682. [DOI] [PubMed] [Google Scholar]
  4. Nanotoxicology: Characterization, Dosing and Health Effects; Monteiro-Riviere N. A.; Tran C. L., Eds.; Informa Healthcare: New York, 2007; pp 1–458. [Google Scholar]
  5. Aillon K. L.; Xie Y.; El-Gendy N.; Berkland C. J.; Forrest M. L. Effects of nanomaterial physicochemical properties on in vivo toxicity. Adv. Drug Delivery Rev. 2009, 61, 457–466. 10.1016/j.addr.2009.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Buzea C.; Pacheco I. I.; Robbie K. Nanomaterials and nanoparticles: sources and toxicity. Biointerphases 2007, 2, MR17–MR71. 10.1116/1.2815690. [DOI] [PubMed] [Google Scholar]
  7. Jeng H. A.; Swanson J. Toxicity of metal oxide nanoparticles in mammalian cells. J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng. 2006, 41, 2699–2711. 10.1080/10934520600966177. [DOI] [PubMed] [Google Scholar]
  8. Fu P. P.; Xia Q.; Hwang H. M.; Ray P. C.; Yu H. Mechanisms of nanotoxicity: Generation of reactive oxygen species. J. Food Drug Anal. 2014, 22, 64–75. 10.1016/j.jfda.2014.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Sarkar A.; Ghosh M.; Sil P. C. Nanotoxicity: oxidative stress mediated toxicity of metal and metal oxide nanoparticles. J. Nanosci. Nanotechnol. 2014, 14, 730–743. 10.1166/jnn.2014.8752. [DOI] [PubMed] [Google Scholar]
  10. Abdal Dayem A.; Hossain M. K.; Lee S. B.; Kim K.; Saha S. K.; Yang G. M.; Choi H. Y.; Cho S. G. The Role of Reactive Oxygen Species (ROS) in the Biological Activities of Metallic Nanoparticles. Int. J. Mol. Sci. 2017, 18, 120 10.3390/ijms18010120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Shah S. A.; Yoon G. H.; Ahmad A.; Ullah F.; Amin F. U.; Kim M. O. Nanoscale-alumina induces oxidative stress and accelerates amyloid beta (Aβ) production in ICR female mice. Nanoscale 2015, 7, 15225–15237. 10.1039/C5NR03598H. [DOI] [PubMed] [Google Scholar]
  12. Golbamaki N.; Rasulev B.; Cassano A.; Robinson R. L. M.; Benfenati E.; Leszczynski J.; Cronin M. T. D. Genotoxicity of metal oxide nanomaterials: review of recent data and discussion of possible mechanisms. Nanoscale 2015, 7, 2154–2198. 10.1039/C4NR06670G. [DOI] [PubMed] [Google Scholar]
  13. Wang D.; Lin Z.; Wang T.; Yao Z.; Qin M.; Zheng S.; Lu W. Where does the toxicity of metal oxide nanoparticles come from: the nanoparticles, the ions, or a combination of both?. J. Hazard. Mater. 2016, 308, 328–334. 10.1016/j.jhazmat.2016.01.066. [DOI] [PubMed] [Google Scholar]
  14. Ai J.; Biazar E.; Jafarpour M.; Montazeri M.; Majdi A.; Aminifard S.; Zafari M.; Akbari H. R.; Rad H. G. Nanotoxicology and nanoparticle safety in biomedical designs. Int. J. Nanomed. 2011, 6, 1117–1127. 10.2147/IJN.S16603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Singh A. V.; Laux P.; Luch A.; Sudrik C.; Wiehr S.; Wild A. M.; Santomauro G.; Bill J.; Sitti M. Review of emerging concepts in nanotoxicology: Opportunities and challenges for safer nanomaterial design. Toxicol. Mech. Methods 2019, 29, 378–387. 10.1080/15376516.2019.1566425. [DOI] [PubMed] [Google Scholar]
  16. Fadeel B.Handbook of Safety Assessment of Nanomaterials: From Toxicological Testing to Personalized Medicine; CRC Press: Florida, 2014. [Google Scholar]
  17. Chen R.; Qiao J.; Bai R.; Zhao Y.; Chen C. Intelligent testing strategy and analytical techniques for the safety assessment of nanomaterials. Anal. Bioanal. Chem. 2018, 410, 6051–6066. 10.1007/s00216-018-0940-y. [DOI] [PubMed] [Google Scholar]
  18. ECHA. The Use of Alternatives to Testing on Animals for the REACH Regulation; ECHA: Helsinki, Finland, 2017; p 103.
  19. Gellatly N.; Sewell F. Regulatory acceptance of in silico approaches for the safety assessment of cosmetic-related substances. Comput. Toxicol. 2019, 11, 82–89. 10.1016/j.comtox.2019.03.003. [DOI] [Google Scholar]
  20. Burgdorf T.; Piersma A. H.; Landsiedel R.; Clewell R.; Kleinstreuer N.; Oelgeschläger M.; Desprez B.; Kienhuis A.; Bos P.; de Vries R.; de Wit L.; Seidle T.; Scheel J.; Schönfelder G.; van Benthem J.; Vinggaard A. M.; Eskes C.; Ezendamb J. Workshop on the validation and regulatory acceptance of innovative 3R approaches in regulatory toxicology—Evolution versus revolution. Toxicol. In Vitro 2019, 59, 1–11. 10.1016/j.tiv.2019.03.039. [DOI] [PubMed] [Google Scholar]
  21. Liu R.; Liu H. H.; Ji Z.; Chang C. H.; Xia T.; Nel A. E.; Cohen Y. Evaluation of toxicity ranking for metal oxide nanoparticles via an in vitro dosimetry model. ACS Nano 2015, 9, 9303–9313. 10.1021/acsnano.5b04420. [DOI] [PubMed] [Google Scholar]
  22. Raies A. B.; Bajic V. B. In silico toxicology: computational methods for the prediction of chemical toxicity. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2016, 6, 147–172. 10.1002/wcms.1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Le T. C.; Yin H.; Chen R.; Chen Y.; Zhao L.; Casey P. S.; Chen C.; Winkler D. A. An Experimental and Computational Approach to the Development of ZnO Nanoparticles that are Safe by Design. Small 2016, 12, 3568–3577. 10.1002/smll.201600597. [DOI] [PubMed] [Google Scholar]
  24. Knudsen T. B.; Keller D. A.; Sander M.; Carney E. W.; Doerrer N. G.; Eaton D. L.; Fitzpatrick S. C.; Hastings K. L.; Mendrick D. L.; Tice R. R.; Watkins P. B.; Whelan M. FutureTox II: in vitro data and in silico models for predictive toxicology. Toxicol. Sci. 2015, 143, 256–267. 10.1093/toxsci/kfu234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Furxhi I.; Murphy F.; Poland C. A.; Sheehan B.; Mullins M.; Mantecca P. Application of Bayesian networks in determining nanoparticle-induced cellular outcomes using transcriptomics. Nanotoxicology 2019, 13, 827–848. 10.1080/17435390.2019.1595206. [DOI] [PubMed] [Google Scholar]
  26. Labouta H. I.; Asgarian N.; Rinker K.; Cramb D. T. Meta-Analysis of Nanoparticle Cytotoxicity via Data-Mining the Literature. ACS Nano 2019, 13, 1583–1594. 10.1021/acsnano.8b07562. [DOI] [PubMed] [Google Scholar]
  27. Bilal M.; Oh E.; Liu R.; Breger J. C.; Medintz I. L.; Cohen Y. Bayesian Network Resource for Meta-Analysis: Cellular Toxicity of Quantum Dots. Small 2019, 15, 1900510 10.1002/smll.201900510. [DOI] [PubMed] [Google Scholar]
  28. Marvin H. J. P.; Bouzembrak Y.; Janssen E. M.; van der Zande M.; Murphy F.; Sheehan B.; Mullins M.; Bouwmeester H. Application of Bayesian networks for hazard ranking of nanomaterials to support human health risk assessment. Nanotoxicology 2017, 11, 123–133. 10.1080/17435390.2016.1278481. [DOI] [PubMed] [Google Scholar]
  29. Luan F.; Kleandrova V. V.; González-Díaz H.; Ruso J. M.; Melo A.; Speck-Planche A.; Cordeiro M. N. D. S. Computer-aided nanotoxicology: Assessing cytotoxicity of nanoparticles under diverse experimental conditions by using a novel QSTR-perturbation approach. Nanoscale 2014, 6, 10623–10630. 10.1039/C4NR01285B. [DOI] [PubMed] [Google Scholar]
  30. Shaw S. Y.; Westly E. C.; Pittet M. J.; Subramanian A.; Schreiber S. L.; Weissleder R. Perturbational profiling of nanomaterial biologic activity. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 7387–7392. 10.1073/pnas.0802878105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Concu R.; Kleandrova V. V.; Speck-Planche A.; Cordeiro M. N. D. S. Probing the toxicity of nanoparticles: A unified in silico machine learning model based on perturbation theory. Nanotoxicology 2017, 11, 891–906. 10.1080/17435390.2017.1379567. [DOI] [PubMed] [Google Scholar]
  32. Furxhi I.; Murphy F.; Mullins M.; Arvanitis A.; Poland C. A. Practices and Trends of Machine Learning Application in Nanotoxicology. Nanomaterials 2020, 10, 116 10.3390/nano10010116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Puzyn T.; Rasulev B.; Gajewicz A.; Hu X.; Dasari T. P.; Michalkova A.; Hwang H. M.; Toropov A.; Leszczynska D.; Leszczynski J. Using nano-QSAR to predict the cytotoxicity of metal oxide nanoparticles. Nat. Nanotechnol. 2011, 6, 175–178. 10.1038/nnano.2011.10. [DOI] [PubMed] [Google Scholar]
  34. Pan Y.; Li T.; Cheng J.; Telesca D.; Zink J. I.; Jiang J. Nano-QSAR modeling for predicting the cytotoxicity of metal oxide nanoparticles using novel descriptors. RSC Adv. 2016, 6, 25766–25775. 10.1039/C6RA01298A. [DOI] [Google Scholar]
  35. Mu Y.; Wu F.; Zhao Q.; Ji R.; Qie Y.; Zhou Y.; Hu Y.; Pang C.; Hristozov D.; Giesy J. P.; Xing B. Predicting toxic potencies of metal oxide nanoparticles by means of nano-QSARs. Nanotoxicology 2016, 10, 1207–1214. 10.1080/17435390.2016.1202352. [DOI] [PubMed] [Google Scholar]
  36. Randić M. Generalized molecular descriptors. J. Math. Chem. 1991, 7, 155–168. 10.1007/BF01200821. [DOI] [Google Scholar]
  37. Choi J.-S.; Ha M. K.; Trinh T. X.; Yoon T. H.; Byun H.-G. Towards a generalized toxicity prediction model for oxide nanomaterials using integrated data from different sources. Sci. Rep. 2018, 8, 6110 10.1038/s41598-018-24483-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Choi J.-S.; Trinh T. X.; Yoon T.-H.; Kim J.; Byun H.-G. Quasi-QSAR for predicting the cell viability of human lung and skin cells exposed to different metal oxide nanomaterials. Chemosphere 2019, 217, 243–249. 10.1016/j.chemosphere.2018.11.014. [DOI] [PubMed] [Google Scholar]
  39. Furxhi I.; Murphy F. Predicting In Vitro Neurotoxicity Induced by Nanoparticles Using Machine Learning. Int. J. Mol. Sci. 2020, 21, 5280 10.3390/ijms21155280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Trinh T. X.; Ha M. K.; Choi J. S.; Byun H. G.; Yoon T. H. Curation of datasets, assessment of their quality and completeness, and nanoSAR classification model development for metallic nanoparticles. Environ. Sci.: Nano 2018, 5, 1902–1910. 10.1039/C8EN00061A. [DOI] [Google Scholar]
  41. Furxhi I.; Murphy F.; Mullins M.; Arvanitis A.; Poland A. C. Nanotoxicology data for in silico tools. A literature review. Nanotoxicology 2020, 14, 612–637. 10.1080/17435390.2020.1729439. [DOI] [PubMed] [Google Scholar]
  42. Ha M. K.; Trinh T. X.; Choi J. S.; Maulina D.; Byun H. G.; Yoon T. H. Toxicity Classification of Oxide Nanomaterials: Effects of Data Gap Filling and PChem Score-based Screening Approaches. Sci. Rep. 2018, 8, 3141 10.1038/s41598-018-21431-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Japkowicz N.; Stephen S. The class imbalance problem: A systematic study. Intell. Data Anal. 2002, 6, 429–449. 10.3233/IDA-2002-6504. [DOI] [Google Scholar]
  44. OECD. Guidance Document on the Validation of (Quantitative) Structure-Activity Relationship [(Q)SAR]] Models; OECD Publishing: Paris, France, 2014.
  45. Jha S. K.; Yoon T. H.; Pan Z. Multivariate statistical analysis for selecting optimal descriptors in the toxicity modeling of nanomaterials. Comput. Biol. Med. 2018, 99, 161–172. 10.1016/j.compbiomed.2018.06.012. [DOI] [PubMed] [Google Scholar]
  46. Kar S.; Gajewicz A.; Puzyn T.; Roy K.; Leszczynski J. Periodic table-based descriptors to encode cytotoxicity profile of metal oxide nanoparticles: A mechanistic QSTR approach. Ecotoxicol. Environ. Saf. 2014, 107, 162–169. 10.1016/j.ecoenv.2014.05.026. [DOI] [PubMed] [Google Scholar]
  47. Guyon I.; Elisseeff A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
  48. Faraway J. J. Data splitting strategies for reducing the effect of model selection on inference. Comput. Sci. Stat. 1998, 30, 332–341. [Google Scholar]
  49. Singh N. D.; Dhall A.. Clustering and Learning from Imbalanced Data. 2018, arXiv:181100972. arXiv.org e-Print archive. https://arxiv.org/abs/1811.00972.
  50. Chawla N. V.; Bowyer K. W.; Hall L. O.; Kegelmeyer W. P. SMOTE: synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. 10.1613/jair.953. [DOI] [Google Scholar]
  51. Hosmer D. W. Jr.; Lemeshow S.; Stanley L.; Sturdivant R. X.. Applied Logistic Regression; John Wiley & Sons, 2013; Vol. 398. [Google Scholar]
  52. Breiman L. Random forests. Mach. Learn. 2001, 45, 5–32. 10.1023/A:1010933404324. [DOI] [Google Scholar]
  53. Chang C.-C.; Lin C.-J. LIBSVM: a library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. 10.1145/1961189.1961199. [DOI] [Google Scholar]
  54. Rumelhart D. E.; Hinton G. E.; Williams R. J. Learning Representations by BackPropagating Errors. Nature 1986, 323, 533–536. 10.1038/323533a0. [DOI] [Google Scholar]
  55. Bergmeir C.; Benítez J. M. Neural Networks in R Using the Stuttgart Neural Network Simulator: RSNNS. J. Stat. Software 2012, 46, 1–26. 10.18637/jss.v046.i07. [DOI] [Google Scholar]
  56. Kuhn M. Building Predictive Models in R Using the caret Package. J. Stat. Software 2008, 28, 1–26. 10.18637/jss.v028.i05. [DOI] [Google Scholar]
  57. Sahigara F.; Kamel M.; Ballabio D.; Mauri A.; Consonni V.; Todeschini R. Comparison of Different Approaches to Define the Applicability Domain of QSAR Models. Molecules 2012, 17, 4791–4810. 10.3390/molecules17054791. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Chen J. J.; Tsai C. A.; Young J. F.; Kodell R. L. Classification ensembles for unbalanced class sizes in predictive toxicology. SAR QSAR Environ. Res. 2005, 16, 517–529. 10.1080/10659360500468468. [DOI] [PubMed] [Google Scholar]
  59. Gómez D.; Rojas A. An empirical overview of the No Free Lunch theorem and its effect on real-world machine learning classification. Neural Comput. 2016, 28, 216–228. 10.1162/NECO_a_00793. [DOI] [PubMed] [Google Scholar]
  60. Garson G. D. Interpreting Neural Network Connection Weights. Artif. Intell. Expert 1991, 6, 46–51. 10.1016/0954-1810(91)90015-G. [DOI] [Google Scholar]
  61. Olden J. D.; Jackson D. A. Illuminating the ‘black box’: A randomization approach for understanding variable contributions in artificial neural networks. Ecol. Modell. 2002, 154, 135–150. 10.1016/S0304-3800(02)00064-9. [DOI] [Google Scholar]
  62. Olden J. D.; Joy M. K.; Death R. G. An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data. Ecol. Modell. 2004, 178, 389–397. 10.1016/j.ecolmodel.2004.03.013. [DOI] [Google Scholar]
  63. Beck M. NeuralNetTools: Visualization and Analysis Tools for Neural Networks. J. Stat. Software 2018, 85, 1–20. 10.18637/jss.v085.i11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Lipton Z. C.The Mythos of Model Interpretability. 2017, arXiv:1606.03490. arXiv.org e-Print archive. https://arxiv.org/abs/1606.03490.
  65. Lek S.; Delacoste M.; Baran P.; Dimopoulos I.; Lauga J.; Aulagnier S. Application of Neural Networks to Modelling Nonlinear Relationships in Ecology. Ecol. Modell. 1996, 90, 39–52. 10.1016/0304-3800(95)00142-5. [DOI] [Google Scholar]
  66. Kleandrova V. V.; Luan F.; González-Díaz H.; Ruso J. M.; Melo A.; Speck-Planche A.; Cordeiro M. N. D. S. Computational ecotoxicology: Simultaneous prediction of ecotoxic effects of nanoparticles under different experimental conditions. Environ. Int. 2014, 73, 288–294. 10.1016/j.envint.2014.08.009. [DOI] [PubMed] [Google Scholar]
  67. Trinh T. X.; Choi J. S.; Jeon H.; Byun H. G.; Yoon T. H.; Kim J. Quasi-SMILES-Based Nano-Quantitative Structure–Activity Relationship Model to Predict the Cytotoxicity of Multiwalled Carbon Nanotubes to Human Lung Cells. Chem. Res. Toxicol. 2018, 31, 183–190. 10.1021/acs.chemrestox.7b00303. [DOI] [PubMed] [Google Scholar]
  68. Oh E.; Liu R.; Nel A.; Gemill K. B.; Bilal M.; Cohen Y.; Medintz I. L. Meta-analysis of cellular toxicity for cadmium-containing quantum dots. Nat. Nanotechnol. 2016, 11, 479–486. 10.1038/nnano.2015.338. [DOI] [PubMed] [Google Scholar]
  69. Horev-Azaria L.; Kirkpatrick C. J.; Korenstein R.; Marche P. N.; Maimon O.; Ponti J.; Romano R.; Rossi F.; Golla-Schindler U.; Sommer D.; Uboldi C.; Unger R. E.; Villiers C. Predictive Toxicology of Cobalt Nanoparticles and Ions: Comparative In Vitro Study of Different Cellular Models Using Methods of Knowledge Discovery from Data. Toxicol. Sci. 2011, 122, 489–501. 10.1093/toxsci/kfr124. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c01076_si_001.pdf (400.5KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES