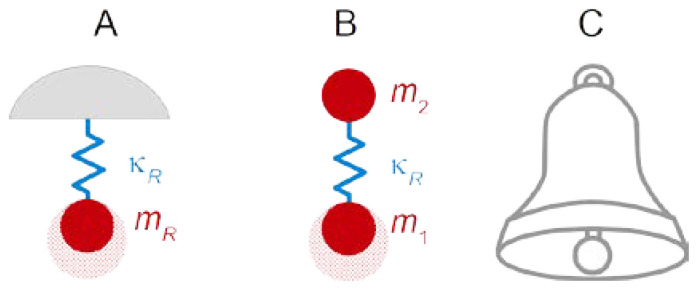
Figure 1.

(A) The simplest possible harmonic resonator. A mass is linked to a rigid wall across a spring. The resonance frequency is ${\mathsf{\omega }}_0 \approx {\left({\mathsf{\kappa }}_{\mathrm{R}}{/m}_{\mathrm{R}}\right)}^{1/2}$. If $m_{\mathrm{R}}$ increases, the resonance frequency decreases in consequence. (B) A resonator abandoning the rigid wall. Two masses are linked across a spring. The resonance frequency is given as ${\mathsf{\omega }}_0 \approx {\left({\mathsf{\kappa }}_{\mathrm{R}}/\mu \right)}^{1/2}$, where µ is the reduced mass (µ = $m_1{m}_2$ /($m_1$ + $m_2$)). Again, increasing one of the two masses will lower the resonance frequency. The diagram in (B) contains discrete elements, similar to the equivalent lumped-element circuits discussed in Section 8.4. (C) Contrasting to the resonators in (A,B), the bell does not consist of discrete masses and springs. It is an elastic body with a certain shape, made from materials with a certain density and stiffness. Finding its resonance frequencies (plural) is a classical problem of acoustics. For any given resonance, one may construct an equivalent lumped-element model containing discrete elements (as in (A) or (B)), which reproduces this one resonance. In principle, one might tune the bell by gluing weights to its rim. The common practice rather is to remove metal in annular rings, usually from the inside [14]. That changes both the effective mass and the effective spring constant. The focus then is not usually on the absolute frequency of the fundamental mode, but rather on the ratios between the overtone frequencies and the fundamental frequency. These ratios govern the perception of the bell’s sound.