Quantum Chemistry Calculations for Metabolomics

Abstract

A primary goal of metabolomics studies is to fully characterize the small-molecule composition of complex biological and environmental samples. However, despite advances in analytical technologies over the past two decades, the majority of small molecules in complex samples are not readily identifiable due to the immense structural and chemical diversity present within the metabolome. Current gold-standard identification methods rely on reference libraries built using authentic chemical materials (“standards”), which are not available for most molecules. Computational quantum chemistry methods, which can be used to calculate chemical properties that are then measured by analytical platforms, offer an alternative route for building reference libraries, i.e., in silico libraries for “standards-free” identification. In this review, we cover the major roadblocks currently facing metabolomics and discuss applications where quantum chemistry calculations offer a solution. Several successful examples for nuclear magnetic resonance spectroscopy, ion mobility spectrometry, infrared spectroscopy, and mass spectrometry methods are reviewed. Finally, we consider current best practices, sources of error, and provide an outlook for quantum chemistry calculations in metabolomics studies. We expect this review will inspire researchers in the field of small-molecule identification to accelerate adoption of in silico methods for generation of reference libraries and to add quantum chemistry calculations as another tool at their disposal to characterize complex samples.

1. Introduction

1.1. Growth and Impact of the Omics

Current basic and applied research of living systems occurs amid several rapidly evolving scientific paradigms, omics (e.g., genomics, transcriptomics, proteomics, and metabolomics),¹⁻⁷ systems biology,⁸⁻¹⁰ and synthetic biology,¹¹⁻¹³ that influence the researcher to look broadly at the holistic system or organism under study. Propelled by key developments of the Information Age, these scientific paradigms encourage scientists to aim for the comprehensive characterization and quantification of the relevant functional units of a cell, organ, organism, or entire system (e.g., soil) and to develop computational models that capture and explain the interactions between and among these units that influence the overall system (Figure 1). At the lowest level, the units that comprise those systems are genes, transcripts, proteins, and metabolites; these units are responsible for the mechanisms by which interactions occur and lead to higher-level system functions and properties. Here, we use “metabolites” to refer not only to small molecules involved in primary metabolism but also to secondary (or “specialized”) metabolites. Secondary metabolites are typically defined as molecules that are not directly involved in organism growth, development, or reproduction¹⁴⁻¹⁶ but instead are produced as a consequence of interactions with other organisms and the environment (e.g., signaling, defense/deterrence, and larger biomolecule degradation).¹⁷⁻²⁰ Related small molecules that are equally important include polar and nonpolar lipids and anthropogenic molecules, such as pesticides, fertilizers, and pharmaceutical products. Similarly, glycans are polysaccharide moieties often bound to proteins on cell surfaces important for cell recognition but also may be bound to lipids or occur freely after enzymatic release.

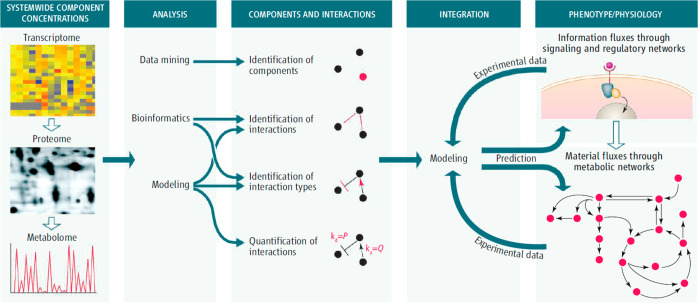
Figure 1.

Systems biology paradigm. Systems biology studies employ omics approaches to comprehensively identify and quantify the functional units of the system under study. One or more omics approach is used to perform measurements of genes, transcripts, proteins, and metabolites, the data are analyzed and integrated, and computational models are used to interpret the results, often with the goal of obtaining a predictive understanding of the system to then manipulate it in a directed fashion. Reproduced with permission from ref (8). Copyright 2007 AAAS.

The measurement of each of the classes of biomolecules that comprise low-level functional units has been enabled by their respective omics paradigm, genomics, transcriptomics, proteomics, metabolomics, lipidomics, and glycomics (Figure 2), and the numbers of publications including data from such studies has steadily increased over the last two decades (Figure 3). Major funding agencies have increasingly recognized the high data yield of omics approaches and their potential to generate new biological and biomedical hypotheses. Many research studies today include one or more types of omics, and many research consortia, centers, and cores focus on multiomics approaches to studying health and disease or provide omics measurement services to clients. Indeed, the U.S. National Institutes of Health (NIH) committed >$200 M in 2019–2020 to fund 266 grants or subgrants that include some aspect of omics data collection or analysis in their proposed research (NIH RePORTER search; keyword “omic” and limited to project abstracts).

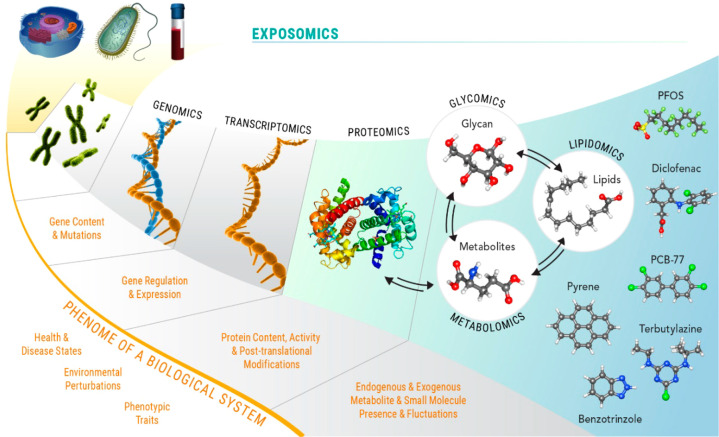
Figure 2.

Omics. The approaches (and philosophies) for comprehensively identifying and quantifying genes, transcripts, proteins, and metabolites are termed genomics, transcriptomics, proteomics, and metabolomics, respectively. Lipidomics is the subdiscipline of metabolomics that addresses the measurement of polar and nonpolar lipids. Glycomics is the omics devoted to the comprehensive measurement of free and protein-bound glycans (as well as glycolipids, i.e., lipid-bound glycans). The exposome includes all endogenous and exogenous exposures and unites transcriptomics, proteomics, metabolomics, lipidomics, and glycomics and includes measurement of anthropogenic molecules. Modified with permission from ref (28) under the Attribution-NonCommercial-No Derivatives 4.0 Unported License (http://creativecommons.org/licenses/by-nc-nd/4.0). Modified with permission from ref (29). Copyright 2016 Springer Nature.

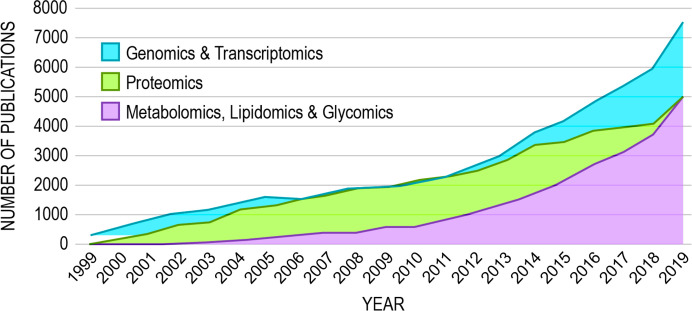
Figure 3.

Omics publication trends 1999–2019. The numbers of publications including genomics, transcriptomics, proteomics, metabolomics, lipidomics, and glycomics approaches have steadily increased in the last two decades, linearly from 1999 to 2009 and exponentially thereafter. Results culminated from PubMed keyword searches of “genomics,″ “transcriptomics,” “proteomics,” “metabolomics” (and “metabonomics”), “lipidomics,” and “glycomics” and limited to appearance in publication title or abstract. Genomics and transcriptomics publications are combined because these approaches rely on sequencing technologies. Metabolomics, lipidomics, and glycomics publications are also combined because comprehensive analysis of these molecular types typically rely on mass spectrometry (MS) approaches but often involve other technology (such as nuclear magnetic resonance spectroscopy).

Omics studies to date have yielded important discoveries of the roles of functional biomolecules or of the genes and pathways that encode or regulate them. For example, in the early 1990s, genomics-based research led to the discovery of two cancer-susceptibility genes, BRCA1 and BRCA2,²¹⁻²⁵ that have revolutionized breast cancer screening. Women who inherit certain mutations in BRCA1 or BRCA2 have 72% and 69% risk, respectively, of developing breast cancer by age 80.²⁶ Mutations in these genes also increase the risk of ovarian cancer.²⁶

In 2004, Zhang and colleagues used a proteomics approach to analyze sera from over 500 individuals with various ovarian cancers and benign pelvic masses in a five-laboratory, case-control study and using a robust study design.²⁷ A number of candidate protein biomarkers were identified, immunoassays were developed for subsequent validation in independent cohorts, and the results indicated that the marker panel could discriminate between benign and malignant ovarian tumors. The research group then worked collaboratively with the U.S. Food and Drug Administration (FDA) to develop an approved assay, and the FDA provided clearance in 2009. The final assay, OVA1, provides >90% sensitivity and 90% specificity for women with an ovarian tumor and for whom surgery is planned when combined with other data. The OVA1 assay is now commercially available from ASPiRA Laboratories to detect ovarian cancer risk in women with planned surgery for a pelvic mass.

Perhaps the most important impact of metabolomics to date is the contribution of early generation approaches to the identification of and monitoring for inborn errors of metabolism,^30,31 which are typically characterized by accumulation of high levels of key metabolites in blood and urine of those afflicted. The first disease identified through newborn screening was phenylketonuria (PKU), which is diagnosed in part based on high levels of circulating phenylalanine due to mutations in the gene encoding the hepatic enzyme phenylalanine hydroxylase.³² If undetected or left untreated, PKU can lead to significant intellectual disability, among other ailments.³³ Today, every state in the U.S. supports screening programs for a wide range of inborn errors of metabolism; for example, Washington State currently tests for 36 disorders, and California state law now requires screening for 80 congenital and genetic disorders in all newborns.

1.2. High Throughput Omics Measurements

The analytical tools used for comprehensive omics measurements vary according to the biochemical nature of the molecules involved. The foundational knowledge of the chemical composition and molecular structure of DNA³⁴⁻³⁶ and the molecular biology associated with the molecule³⁷⁻³⁹ are the primary elements that have enabled present-day technology for rapid, comprehensive, and cost-effective determination of DNA composition and order (“sequencing”). DNA is a relatively simple biomolecule, consisting of two complementary, polymeric strands comprising repeating units of just four nucleotide bases. A variety of next-generation sequencing technologies are available today; however, at the highest level, all genomic sequencing begins with isolation of DNA from a sample, the shearing of the double-stranded molecule to a single strand, and the subsequent elongation of a short complementary primer sequence through sequential addition of free nucleotides by the action of the enzyme DNA polymerase.³ The sequential incorporation of free nucleotides into the growing DNA chain is monitored by fluorescence detection of fluorophores bound to the nucleotides. The inherent specificities of DNA polymerase, hydrogen bonding between complementary pyrimidine and purine nucleotides, and nucleotide-bound fluorophores, combined with the accuracy of current sequencing data processing algorithms, all contribute to genomic sequencing results with very low error rates (typically less than 1%). The massive parallelization available in modern sequencing instruments allows for nearly complete coverage of a genome in a relatively short time and at low cost. Technologies for sequencing of RNA (i.e., transcriptomics) are similar.

Proteins, like DNA and RNA, are polymers of repeating units of 20 amino acids. Unlike DNA and RNA, no molecular biology can be leveraged to determine their sequence in such a complete, accurate, and cost-effective manner. Instead, proteins are normally “sequenced” in proteomics analyses using tandem mass spectrometry (MS/MS). In the shotgun proteomics paradigm, proteins are digested into their constituent peptides using the enzyme trypsin, which cleaves on the carboxyl side of arginine and lysine residues. This process generates peptides of manageable size that are amenable to separation using liquid chromatography (LC), ionization using electrospray (ESI), and gas-phase fragmentation using, for example, collision-induced dissociation (CID).¹ During CID, peptides typically dissociate at the peptide bond, producing fragmentation spectra with constituent m/z corresponding to different sizes of the peptide in question, minus one or more constituent amino acids in sequence (i.e., so-called “ion ladders”). Various software tools have been developed for in silico prediction of peptide fragmentation spectra.^40,41 These software tools essentially generate comprehensive reference libraries of predicted peptide spectra and for every protein suspected of being present in the sample. The predicted fragmentation spectra generated by these algorithms are based on peptides derived in silico from reference protein sequences, and the reference protein sequences are in turn generated from the genome of an organism of interest, thus showing the intimate relationship between genomics and proteomics. Because of comparatively higher errors in peptide identification using MS-based proteomics (compared to gene sequencing), approaches were developed to provide a measure of confidence in the results from proteomics data processing tools.⁴² The most commonly implemented approach for estimating and controlling the error rate in proteomics data processing is the target–decoy database approach,⁴³ which allows researchers to control the degree of false identifications (i.e., the false discovery rate) by setting minimum peptide identification score thresholds that both maximize the numbers of confidently identified peptides while minimizing the numbers of incorrect identifications.

1.3. Major Roadblocks in Metabolomics

Metabolomics is the least mature of the omics. Although the average molecular formula composition of a metabolite does not differ significantly from that of a peptide,⁴⁴ metabolite structures are not constrained to a template like DNA, RNA, and proteins. Their chemical diversity is governed only by what constitutes a thermodynamically stable structure (>10³³–10¹⁶⁰ possible structures for molecules, depending on the number of atoms and elements considered^45,46). Moreover, the concentrations of metabolites vary by over 10 orders of magnitude. Because of this immense chemical diversity and consequent broad range of physicochemical properties and abundances, multiple analytical technologies are employed in comprehensive metabolomics studies to achieve high coverage of the metabolome. The chemical diversity of the metabolome has also precluded the development of analytical paradigms providing high-throughput (i.e., automated) and accurate identifications of metabolites with associated estimates of false discovery.

For novel molecules, using advanced ultrahigh resolution MS, the chemical formula can be readily determined with high confidence, but the organization of the constituent atoms into chemical structures cannot be unambiguously determined from many possible isomeric compounds with the same molecular formula.⁴⁷ Kind and Fiehn reported that for the molecular formula C₁₅H₁₂O₇, 181, 166, and 129 matches were identified in a search of the chemicals in the Chemical Abstracts, Beilstein, and Natural Products databases, respectively.⁴⁷ More broadly, within 540 000 molecules selected from the Human Metabolome Database (HMDB)⁴⁸ and the DSSTox database,⁴⁹ 20% of the molecular formulas match more than five compounds, and 474 000 molecules have a formula conflict with at least one other molecule. Thus, even with other properties such as isotopic signature, chemical structures cannot be unambiguously identified^28,47,50 for novel molecules from mass alone without use of orthogonal analysis (e.g., chromatography, ion mobility, MS/MS) and comparison of experimental data to that from analyses of authentic reference chemicals. This problem has been especially prevalent in spatially resolved metabolomics (i.e., imaging) applications, where, until recently, it has been challenging to add orthogonal dimensions of data for improved molecular identification.⁵¹⁻⁵⁴ Nuclear magnetic resonance (NMR) spectroscopy is an established tool for assignment of chemical structures to novel molecules but requires higher sample concentration and purity, limiting its utility for structural elucidation of novel molecules in a high throughput, comprehensive manner. However, small-volume NMR probes⁵⁵⁻⁵⁷ at high field strengths are greatly improving the sensitivity limitations, and several approaches of mixture analysis are reducing or eliminating the need for purity.⁵⁸⁻⁶⁰ Likewise, microcrystal electron diffraction (MicroED) has recently been demonstrated for direct and confident structure confirmation.⁶¹

For measuring known molecules, efficient analytical methodologies for confident identification of large numbers of metabolites in high throughput metabolomics studies are gas chromatography–MS (GC-MS), LC-MS, and NMR. Here, metabolite identification is achieved by comparison of experimental data to reference libraries containing data from analyses of authentic chemical standards. Such approaches satisfy the recommendations of the Metabolomics Standards Initiative (MSI) of the Metabolomics Society for confident metabolite identification.^62,63 However, the reliance of these approaches on reference data generated through analyses of authentic chemical standards is a significant limitation because the number of chemicals available for purchase is very limited relative to the number of molecules proposed to exist in the universe.⁶⁴ For example, HMDB represents <5% of the estimated total metabolite space across multiple organisms, and only ∼10% of HMDB molecules are represented by readily available authentic chemical standards⁶⁵ (verified through custom Python scripts to search known vendors).^7,66 Further, one of the largest repositories of authentic reference spectra, the Wiley Registry, contains data for nearly 300 000 molecules, or just <1% of known chemicals when considering the ChemSpider, PubChem, and American Chemical Society’s CAS databases, which contain entries for tens of millions of chemicals.⁶⁷

There is therefore a tremendous disparity between the numbers of metabolites, exposure molecules, and xenometabolites that can be confidently identified in metabolomics studies when adhering to current MSI guidelines versus the number of molecules postulated to fill “chemical space.” A reasonable approach to increasing the amount of reference data for use in small-molecule identification is through in silico means. This review will discuss the potential for quantum chemistry approaches to contribute to the calculation of, for example, chemical properties and reference spectra for metabolites and other small chemicals, which can be used to aid molecular identification in complex samples, thereby overcoming a significant obstacle remaining in the field of metabolomics.

1.4. Quantum Chemical Applications

1.4.1. Historical Overview

The purpose of this section is to illustrate the promise of quantum chemistry for metabolomics, including prediction of quantities relevant to NMR, MS, and other methods. While we summarize some approaches here, numerous reviews and books are available that cover the applications of quantum chemistry in various subfields in greater detail.

Quantum chemistry is concerned with calculating the states and properties of the electrons in a molecular system using the laws of quantum mechanics (QM). According to the time-independent Schrödinger equation, the stationary quantum states of a system (i.e., those with definite energy) are eigenfunctions of a Hamiltonian operator representing the electron kinetic energy and interactions among electrons and nuclei. This review will mostly limit itself to a conceptual framework bound by several assumptions such as the separation of nuclear kinetic and electronic energy scales (the Born–Oppenheimer approximation), nonrelativistic electronic energy scales, and the absence of fine structure-producing effects such as spin–orbit coupling. These assumptions are often made for computational efficiency without significantly sacrificing accuracy for many applications (including most presented here), although care must be taken when simulating systems where these effects are important, such as nonradiative relaxation around a conical intersection⁶⁸ or spin crossover induced by heavier elements.⁶⁹

Schrödinger’s equation does not have an analytic solution for the general many-electron problem. Exact numerical solutions are computationally inaccessible for all but the smallest systems. Thus, quantum chemistry involves finding approximate solutions that give the optimal compromise between accuracy and computational cost for problems of chemical interest. The Hartree–Fock theory^70,71 and density functional theory (DFT),⁷²⁻⁷⁴ two of the very first quantum chemistry methods, were conceived in the 1920s while QM was still in its infancy. Significant advances were made in the 1960s and 1970s, partially motivated by the revolutions in technology and exponential increases in processing power that continued through the early 2000s. In 1998, John Pople and Walter Kohn were recognized with the Nobel Prize in Chemistry for their pioneering contributions in molecular quantum chemistry,^75,76 and one of its principal branches, Kohn–Sham DFT (KS-DFT).^77,78 The relationship of quantum chemistry to other molecular simulation approaches is illustrated in Figure 4.

Figure 4.

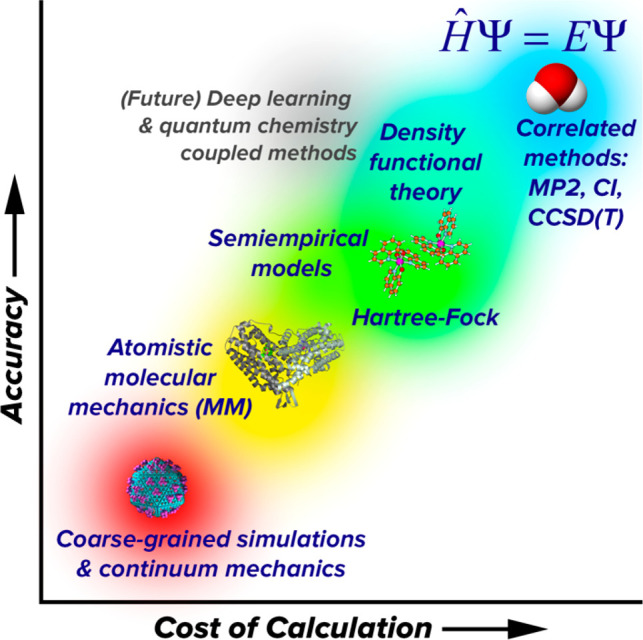
Quantum chemistry methods (upper right) are considered highly accurate but also highly expensive compared to empirical potential-based simulation methods (lower left). Methods that combine physics-based principles with empirical knowledge, such as semiempirical models, density functional theory, and future deep-learning-based methods are promising for improving accuracy without increasing computational cost.

Today, quantum chemistry is a flourishing field and continues to make significant advances both in terms of theoretical methods that afford increasingly accurate and efficient approximations and computational methods that take maximum advantage of available computer hardware and software libraries. It has become common practice for leading research groups in this field to release free or commercial software packages that implement quantum chemistry methods for the broader community to apply to chemical problems. Examples of these software packages include Gaussian,⁷⁹ Q-Chem,⁸⁰ GAMESS,⁸¹ Psi4,⁸² Molpro,⁸³ NWChem,⁸⁴ ORCA,⁸⁵ and TeraChem.^86,87

Quantum chemistry has made significant impacts in the chemical sciences due to its ability to routinely compute many properties of experimental interest with “chemical accuracy”, i.e., accurate enough to make meaningful interpretations and predictions.⁸⁸ The usual working definition of chemical accuracy is that relative energies between two states should have an error of <1 kcal/mol compared to a gold standard, which can be experimental thermochemical data, such as atomization energies,^89,90 or another higher-level calculation. A commonly accepted gold standard calculation is coupled cluster with singles, doubles, and perturbative triples (CCSD(T)/CBS)^91,92 in the complete basis set limit.^93,94 In modern benchmarks, these values are computed indirectly using composite methods such as the Weizmann-n approaches that combine the results of several other calculations.⁹⁵ This approach is not a gold standard for all properties and systems because CCSD(T)/CBS is not a valid approximation for systems with significant multireference electronic character,⁹⁶⁻⁹⁸ such as open-shell transition metal complexes or highly excited electronic states. Moreover, most experiments measure signals from a thermodynamic ensemble of molecules undergoing time evolution and sometimes in a condensed-phase environment, whereas an individual quantum chemistry calculation is carried out on a single molecular structure, which makes comparisons difficult. Simulating experimental observables using quantum chemistry often requires incorporating molecular dynamics (MD) on the quantum chemical potential energy surface (PES), configurational sampling, environmental effects, nuclear quantum effects, and possibly other effects if experimentally relevant. Thus, the definition of accuracy can vary broadly depending on the system and property being considered.

For many methods, it is possible to compute the analytic nuclear gradient of the energy at relatively low additional cost, which enables an efficient optimization of energy-minimized structures and other transition states on the molecular PES.^99,100 This affords a route to predicting the reaction energy and activation energy of hypothetical reaction mechanisms, providing important support for mechanistic understanding of chemical reactivity that is difficult to probe experimentally. A wide range of properties may be computed for a given molecular structure, including electronic and vibrational transition energies, electrostatic moments, and polarizability.¹⁰¹ Calculations of nuclear shielding and internuclear couplings provide a route toward computing NMR observables (section 2.1). Still other properties may be computed from approximate free energy differences, such as redox potential¹⁰² and pK_a.^103,104

Many experimentally measured properties are derived not from a single structure but from a statistical ensemble at finite temperature, which could be simulated implicitly by making a rigid rotor/harmonic oscillator approximation^105,106 or sampled explicitly using MD^107,108 or Monte Carlo (MC)^109−111 methods. Effects of the solvent or other chemical environments are treatable implicitly by using polarizable continuum models¹¹² or explicitly by including molecules of the environment in the calculation, although the latter greatly increases the computational cost and dimensionality of configuration space. The quantum behavior of nuclei manifests as zero-point vibrational energy in the harmonic approximation or can be explicitly simulated using path-integral MD methods.^113−115 Hybrid models such as QM/MM are useful for explicitly modeling portions of the system, such as a solvent or protein environment, using inexpensive force field (FF) models.^116,117

The applicability of quantum chemistry should be considered along several dimensions, including the size of the system, which affects the computational cost, the level of theory and amount of sampling needed to compute a result to desired accuracy and statistical precision, the availability of experimental data to inform the development of better methods and models, the importance and complexity of environmental effects, and last, the accessibility of the computational methods to nonexpert users.

1.4.2. Relative Energies and Equilibrium Structures

A basic building block of quantum chemistry applications is the calculation of relative energy between two chemical states, which may differ in the number of electrons, atoms, and three-dimensional structure. Several classes of relative energies include:

• Ionization energies and electron affinities^118,119

• Proton affinities^120,121

• Bond dissociation energies^122,123

• Atomization energies, the total separation of molecules into constituent atoms

• Isomerization energies^124−126

• Noncovalent interactions^127−129

• Conformational relative energies^130−132

• Reaction energies and activation energies (covered in detail in section 1.4.3)

In all of these cases, the calculation involves taking the difference between two calculated energies, often with the preliminary step of energy minimization. Numerous published benchmark studies describe the accuracy of various quantum chemistry methods versus the gold standard for these properties.^{101,120,133−136}

Relative energies form the foundation of simulations that incorporate more aspects of the experimental system such as the thermodynamic ensemble, time evolution, environment, and nuclear quantum effects. It is important to note that to describe a chemical phenomenon, relative free energies are more meaningful and analogous to experimentally measurable quantities such as redox potential, pK_a, standard reaction free energies/free energies of activation, and equilibrium conformations.

In metabolomics and compound identification applications, the accurate prediction of relative peak heights is of principal importance.^137−139 Because the relative peak heights of adduct ions, i.e., [M + H]⁺, [M + Na]⁺, etc., vary depending on the analyte and solvent conditions, these data can be used in compound identification as discussed in greater detail below.¹⁴⁰ Recent developments in DFT functionals have seen nearly universal incorporation of empirical dispersion corrections^141−143 and consequently a dramatic improvement in accuracy for noncovalent interactions.^129,134,135 Therefore, one potential application of quantum chemistry is to predict the relative peak heights of adduct ions for an analyte by comparison of noncovalent interaction energies.^144,145

1.4.3. Reaction Mechanism Analysis

Perhaps the most widespread application of modern quantum chemistry is the analysis of reaction mechanisms, which may be proposed from chemical intuition or by automated approaches. The basic computational results in these studies are reaction energies and activation barriers for elementary steps, which provide insight into the thermodynamic and kinetic feasibility of the proposed mechanism.^146−150 The reaction rate is proportional to exp[−E_a/RT], where E_a is the activation energy calculated from the potential difference between optimized transition state and reactant structures, R is the thermodynamic gas constant, and T is absolute temperature. The transition state is located at a saddle point on the PES, where the direction of downward curvature corresponds to a vibrational mode of imaginary frequency that leads toward the reactant and product structures on either side. At room temperature, an increase in ∼1.4 kcal/mol of E_a results in a roughly 1 order of magnitude decrease in reaction rate. Calculated E_a values are often used as a screen for room temperature mechanistic feasibility by comparison with a “rule of thumb” value, which typically ranges from 21 to 30 kcal/mol,^151−154 although values have been reported as high as 40 kcal/mol.¹⁵⁵

These calculations neglect the contribution of system-dependent dynamical properties to the reaction rate but are still highly useful for mechanistic screening because computed values of E_a for different mechanistic hypotheses have a wide dynamic range of 0–100 kcal/mol or more. Multiple hypotheses may be compared under the assumption that differences in E_a play the dominant role in the relative rates. Care must be taken to select an appropriate method, as detailed benchmark studies in the literature have shown that many choices of quantum chemistry method and/or basis set could lead to errors of 10 kcal/mol or more.^129,135 Recently developed density functional approximations, such as range-separated hybrid functionals with dispersion correction (e.g., ωB97X-V,¹⁵⁶ M08-HX-D3^135,157) and double-hybrid functionals, are able to achieve accuracy to within 1–3 kcal/mol of the gold standard provided that rather large basis sets, such as def2-TZVPD, are used.¹⁵⁸ However, these methods may be cost prohibitive for larger systems, and all single-reference methods (including most DFT functionals) are suspect for systems that contain strong multireference electronic character. Free energy corrections are also important in reaction mechanism analysis; in particular, the inclusion of translational and rotational entropic contributions has a significant effect on association and dissociation reactions.⁸⁵

A long-term goal of reaction mechanism analysis is to leverage mechanistic insights toward reaction and catalyst design. For example, computations may be used to choose the best candidate from a series of catalysts that follow the same mechanism but differ in their activation energies. Although quantum chemistry is starting to play a more active role alongside experiment in this arena, mechanistic investigations still require significant human and computational effort, and further developments are needed to make truly novel predictions and designs. Automated tools for mechanism generation are a recent development that show promise for making progress in this field.^159−166 Reaction mechanism analysis is important for metabolomics in terms of predicting fragmentation patterns in MS experiments, described later in this article.

1.4.4. Thermodynamic Properties

Quantum chemistry can provide insight into equilibrium properties of a system by accounting for the distribution of states in a thermodynamic ensemble. This is commonly done using simple models; one common approach is to model the molecular partition function using a product of ideal gas, rigid rotor, and harmonic oscillator terms, although several more advanced methods that go beyond this approximation are available.¹⁶⁷ The molecular vibrational frequencies are obtained from the Hessian (second nuclear derivatives) of the electronic energy. Alternatively, the thermodynamic ensemble can be sampled explicitly using MD or MC methods.

Some of the most important experimentally measurable quantities are functions of the free energy difference between two states. These quantities include the standard reduction potential (redox potential) and pK_a, which measure the tendency for a species to gain electrons and protons in solution, respectively. The accuracy of DFT in calculating redox potentials is well established, and it has been hailed as a tool for rational electrocatalyst design.^102,168 Errors in computed values vs experiment can be as small as 0.1–0.2 V, which is small compared to experimental variations across a typical series of redox-active compounds.

The predictions of redox potentials and pK_a values have an important dependence on the choice of solvent model. Widely used implicit solvent models, which are based on a polarizable continuum,^169−171 tend to have lowered accuracy in systems where solute–solvent hydrogen bonding effects are important. Perhaps owing to this difficulty, the sizes of errors in redox potential calculations tend to be more similar within a group of chemically similar compounds but vary more broadly across disparate compounds.¹⁷² Errors incurred by implicit solvent are especially onerous for pK_a calculations, where the addition or removal of a proton often leads to differences in hydrogen bonding interactions. An error in the calculated ΔG of just 1.4 kcal/mol corresponds to a deviation of 1 pK_a unit from experiment.^173,174 The use of explicit solvent models has been shown to yield improvements in the accuracy of pK_a and redox potential calculations,^160,175 but they are much more computationally expensive, requiring significant amounts of sampling of solute and solvent degrees of freedom.

MD and MC are simulation methods that can sample from a thermodynamic ensemble of states. MD propagates the atoms in the system using classical equations of motion, and thermodynamic sampling is achieved by means of a thermostat that perturbs the molecular velocities in order to sample from the constant temperature ensemble. A barostat can similarly be used to perturb simulation cell volumes to sample from the constant pressure ensemble. In principle, MD can be used with any underlying potential function, and it is termed ab initio molecular dynamics (AIMD) when the potential is calculated using quantum chemistry methods. MC, on the other hand, performs sampling by making randomized proposed moves through configuration space with acceptance probabilities calculated from ratios of Boltzmann factors. Both methods have been applied to compute equilibrium properties of molecular and solid substances.

For ordinary substances such as liquid water, good agreement with experimental data can be reached for properties such as the bulk density and radial distribution function.^176,177 However, nuclear quantum effects need to be explicitly accounted for using path integral MD^113−115 or otherwise roughly approximated by increasing the simulation temperature. Because ab initio methods are not parametrized to experimental data, they have also been applied to predict new phases of matter at extreme conditions, including superionic phases of ice¹⁷⁸ and metallic phases of hydrogen,¹⁰⁹ which are hypothesized to exist in planetary cores but have yet to be confirmed experimentally.

In metabolomics applications, compounds are often separated based on differences in the strength of intermolecular interactions with immiscible solvent phases.^179−181 The key physical quantities that predict retention time are the octanol–water partition coefficient (log P) or distribution coefficient (log D), which is proportional to the difference in solvation free energies in the two phases.¹⁸² Although empirical models such as neural networks have long been the dominant method for predicting partition coefficients,^183−185 we expect that quantum chemical methods will play an increasingly important role in predicting this important property in the future as sampling methods and computational efficiency continue to improve.

1.4.5. Spectroscopic and Excited State Properties

A variety of quantum chemistry methods are available to model how molecules respond to electromagnetic radiation in a variety of energy regimes. These methods are broadly useful for interpreting and assigning spectra, including in compound identification applications. At the low end of the energy spectrum, NMR shielding tensors and internuclear couplings may be computed using DFT (section 2.1).

Infrared (IR) spectra, which probe molecular vibrations, can be calculated from quantum chemistry in several ways. One type of approach is based on expanding the PES around a minimum energy structure, starting with normal modes obtained from diagonalizing the Hessian matrix. Because this approach ignores higher-order anharmonic effects, method-dependent empirical scaling factors are applied to calculated harmonic vibrational frequencies in order to obtain improved agreement with experiment.¹⁸⁶ Going beyond the harmonic approximation, a fourth-order expansion called a quartic FF¹⁸⁷ can be used in conjunction with vibrational perturbation theory or vibrational configuration interaction to obtain rovibrational spectra including anharmonic effects.^188,189 In the other kind of approach, MD simulations can also be used to simulate IR spectra by taking the Fourier transform of the dipole autocorrelation function.^190,191 This method is useful for obtaining spectra in bulk liquids and macromolecules, where soft degrees of freedom and multiple minima are more prevalent. The application of IR to small molecule identification is discussed in section 2.3.

Visible and ultraviolet (UV) wavelengths induce electronic excitations, which require quantum chemical descriptions of the excited state. Building off of the foundations of Hartree–Fock and DFT, the configuration interaction singles (CIS)¹⁹² and time-dependent DFT (TD-DFT)¹⁹³ methods build a Hamiltonian matrix in the space of single excitations from the reference ground-state wave function, followed by diagonalization to obtain excited state energies. TD-DFT tends to yield root mean-squared errors of ∼0.3 eV in vertical excitation energies for many functionals,¹³³ but the topography of the excited state potential energy surface is incorrect, leading to incorrect descriptions of conical intersections where the excited-state and ground-state energies become degenerate. Multireference wave function methods^194,195 can yield improved accuracy for excited-state potential energy surfaces, which may be applied to light-activated molecular switches and other electronically excited molecules.

The accuracy of the equilibrium structure is usually considered to be secondary to the reproduction of relative energies in most applications. One important exception is in microwave (rotational) spectroscopy experiments that can provide very accurate values of the moments of inertia of gas-phase molecules; these are sensitive to changes in bond lengths to within 10^–13 m and bond angles to within 0.01°.¹²² The most accurate measurements of molecular geometry are derived from these experiments, and highly accurate optimized structures can in turn be used to assign microwave spectra of unknown compounds.¹²³

2. Current Applications and Real Examples

2.1. Nuclear Magnetic Resonance

The main alternative to the MS-based approach to detect metabolites is provided by analytical NMR spectroscopy.^65,196−199 High-resolution NMR analysis is capable of providing accurate structures of a range of molecules including metabolites.²⁰⁰ This is of import in metabolomics, where ultrasensitive mass spectrometry instruments can detect differential mass signals but do not provide enough structural information to structurally characterize a given metabolite.

To bridge the gap between spectroscopic observations and structure the metabolomics field has been turning to the tools of computational chemistry.^201−208 Over the past decade, in silico calculations of NMR chemical shifts have significantly improved in accuracy, affordability, and reliability. The overall improvements in NMR computation come from methodological advancements, increased computational power, as well as complete end-to-end automation of these calculations.^209,210 Therefore, reliable chemical shift calculations are now highly accessible to chemists.

Extensive literature exists in the field of NMR chemical shift computation. For example, Kaupp, Buhl, and Malkin edited a book on the calculation of NMR and electron paramagnetic resonance (EPR) parameters.²¹¹ In 2008, Casabianca and de Dios published an extensive review on ab initio NMR chemical shift calculation.²¹² Bryce and Wasylishen wrote an extensive review, including an overview of the calculation of NMR parameters using ab initio methods.²¹³ Additionally, a review of chemical shielding calculations on proteins, peptides, and amino acids has been provided by Oldfield.²¹⁴ Several applications of chemical shift calculations are described by Facelli’s review.²¹⁵ Gauss and Stanton added electron correlation to the computation of chemical shielding.²¹⁶ Tossell used a cluster model to compute shielding values for crystals,²¹⁷ and Sebastiani reviewed chemical shift calculations in condensed phases.²¹⁸ Benzi et al.(219) and Bagno et al.(220) included solvent effects in chemical shift calculations, and Oldfield included electrostatic effects on chemical shifts and applied this improved method to protein structure determination.²²¹ On the other hand, Hunter et al. discussed the use of semiempirical methods to evaluate chemical shifts²²² as did Merz and co-workers.²²³ For rapid NMR shift computation for larger systems, a QM/MM approach has been described.^224,225 Finally, Bryce and Sward summarized the state-of-the-art for the study of quadrupolar halogens using solid-state NMR.²²⁶

There is an extensive literature of the use of quantum mechanical methods to explore NMR related problems, including the determination of relative stereochemistry^227−229 and NMR assignment of regioisomers.²³⁰ Tantillo, Siebert, and Lodewyk review the use of ab initio and DFT calculations for NMR chemical shift prediction.^231,232 Benchmarking studies for the prediction of chemical shifts with different methods and levels of theory have been reported.^233−235 Further summaries on advancements in the evaluation of chemical shielding values can be found in Jameson and de Dios.^236,237

To the best of our knowledge, the studies mentioned above only considered single conformer data sets for computation of NMR chemical shifts and accuracy assessment. In the case of flexible molecules with multiple conformers, the field is considerably less mature. For flexible molecules (e.g., metabolites or drug-like molecules) with a large chemical space, considering a single conformer for these calculations most likely yields erroneous results.²³⁸ Therefore, to get meaningful NMR data for flexible compounds, a large chemical space (i.e., robust conformational search) needs to be considered. There have been three successful attempts to design an automatic protocol to predict NMR chemical shift of flexible molecules. Willoughby et al., Yesiltepe et al., and Grimme et al. have developed automated approaches for ¹H and ¹³C chemical shift prediction for the nonexpert.^204,209,210 The computational protocol of Willoughby et al. is shown in Figure 5. Another protocol was developed by Xin et al. to compute ¹³C NMR chemical shifts (Figure 6), employing the standard DFT method with an optimized basis set (cc-pVDZ) and a DFT functional (B3LYP) for organic molecules.²³⁹ All of these protocols employ high-level QM methods, yielding accurate and reliable NMR results, but due to the expense of the QM methods used, they are too computationally expensive to handle a large number of samples with unknown structures. Moreover, more complex molecules like metabolites, with many rotatable bonds, offer challenges associated with sampling complex conformational spaces and the extant protocols have yet to be fully validated.

Figure 5.

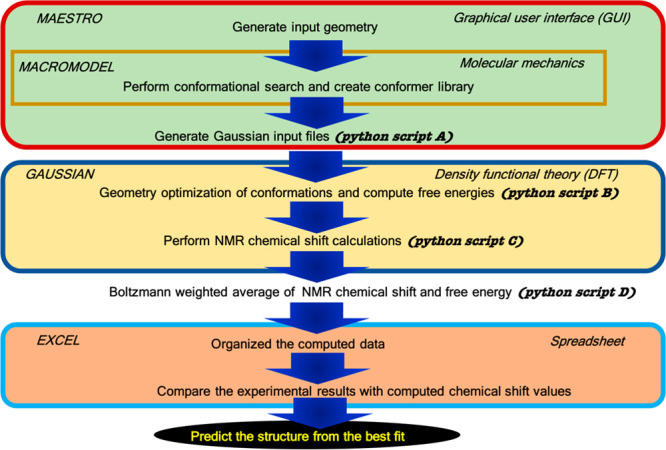
NMR chemical shift calculation protocol developed by Willoughby et al.(204)

Figure 6.

NMR chemical shift calculation protocol developed by Xin et al.(239) Reproduced with permission from ref (239). Copyright 2017 American Chemical Society.

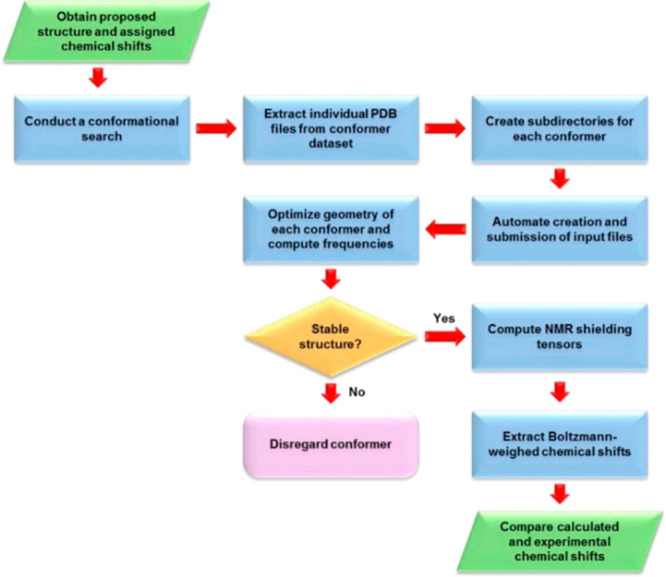
An efficient computational workflow must use the most computational efficient method at each step to accomplish the desired goal. Accurate QM methods are very computationally expensive and should only be used when no other options are available.^240,241 Where possible less expensive FF methods can be used, but attention should be paid to their overall accuracy. Machine learning (ML) methods can also be substituted where appropriate.^242,243 In the approach of Das et al., their workflow takes advantage FF, ML, and QM-based methods to generate structural predictions for medium-size organic molecules including metabolites.²⁴⁴ The pipeline encompasses the following steps (Figure 7): (i) conformation generation using an FF-based method, (ii) filtering the FF generated conformations using the Atomic Simulation Environment- Accurate Neural Network Engine for Molecular Energies (ASE-ANI) model, (iii) clustering of the optimized conformations based on structural similarity to identify chemically unique conformations, (iv) DFT structural optimization of the unique conformations, and (v) DFT NMR chemical shift calculation.²⁴⁴ This protocol can calculate the NMR chemical shifts of a set of molecules using any available combination of DFT theory, solvent model, and NMR-active nuclei, using both user-selected reference compounds and/or linear regression methods. The protocol reduces the overall computational time by 2 orders of magnitude over methods that optimize the conformations using fully ab initio methods yet matches experimental structural observations. The complete protocol provides an efficient way to obtain chemical shifts for conformationally flexible metabolites.

Figure 7.

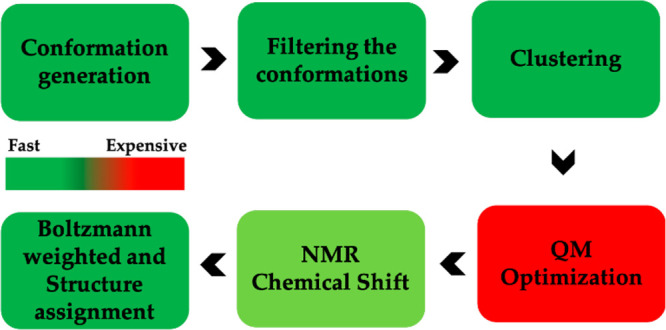
Das and Merz protocol to calculate NMR chemical shift. This protocol includes FF, ML-QM, and standard QM methods to improve efficiency of NMR computation technique with low computational cost.

To illustrate the NMR chemical shift (¹H and ¹³C) protocol of Das and co-workers, the case of folate (C₁₉H₁₉N₇O₆: Figure 8) is presented herein. Folate was run through the workflow illustrated in Figure 7. The detailed results are given in Figure 9 and in Tables 1–Table 3. Overall, the mean absolute error (MAE) values of ¹H and ¹³C are 0.26 and 1.63, respectively, confirming a good agreement of computational data with the experimental chemical shift. MAE values are calculated using eq 1.

1

where δ_i^exp is the experimental NMR chemical shift value of the ith nucleus of a molecule and δ_i is the computed NMR chemical shift of same nucleus. This high-throughput workflow²⁴⁴ can be deployed to obtain the chemical shifts for large collections of candidate metabolite structures to facilitate their characterization.

Figure 8.

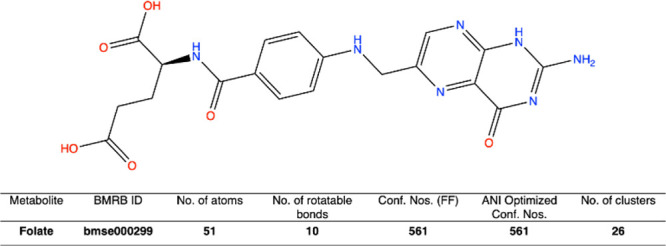
BMRB ID, no. of atoms, no. of rotatable bonds, FF generated conformation, ANI optimized conformations, and no. of clusters are reported for folate molecule.

Figure 9.

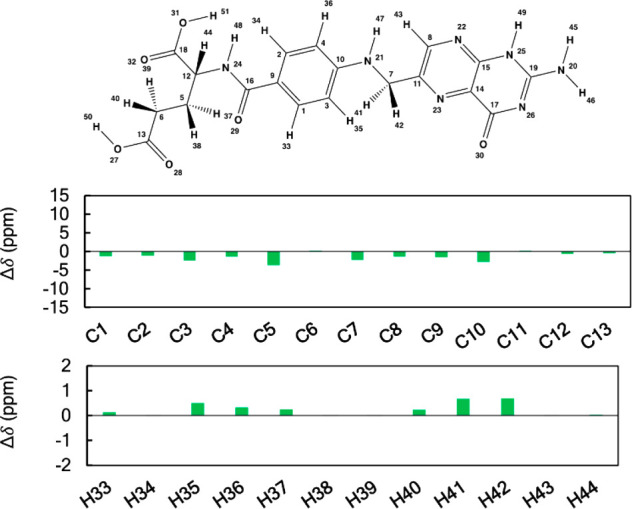
Plots of the differences between the calculated and experimental ¹H and ¹³C NMR chemical shifts of folate. Shielding constants were computed at the B3LYP/6311G+(2d, p) level of theory and converted to linear scaled reference chemical shifts. Values of chemical shift differences are given in ppm.

Table 1. Relative Energies, Boltzmann Factor, and Equilibrium Mole Fraction of All Structurally Distinct Conformations of Folate.

conformation no.	relative energy (kcal)	Boltzmann factor	equilibrium mole fraction
1	0.36	0.55	0.17
2	2.94	0.01	0.00
3	2.34	0.02	0.01
4	2.93	0.01	0.00
5	3.42	0.00	0.00
6	1.65	0.06	0.02
7	2.52	0.01	0.00
8	2.71	0.01	0.00
9	3.09	0.01	0.00
10	6.83	0.00	0.00
11	0.39	0.51	0.16
12	2.91	0.01	0.00
13	1.20	0.13	0.04
14	4.17	0.00	0.00
15	0.46	0.46	0.15
16	2.19	0.02	0.01
17	7.47	0.00	0.00
18	3.82	0.00	0.00
19	1.20	0.13	0.04
20	1.77	0.05	0.02
21	4.44	0.00	0.00
22	6.18	0.00	0.00
23	2.68	0.01	0.00
24	0.00	1.00	0.32
25	3.58	0.00	0.00
26	1.18	0.14	0.04

Table 3. Computed and Available Experimental ¹³C NMR Chemical Shifts for Folate.

atom no.	computed chemical shift (ppm)	experimental chemical shift (ppm)
C1	129.92	131.32
C2	129.99	131.32
C3	111.41	113.93
C4	112.38	113.93
C5	27.20	31.09
C6	37.42	37.09
C7	45.05	47.45
C8	149.48	150.97
C9	150.86	152.47
C10	120.09	123.10
C11	150.75	150.41
C12	57.95	58.65
C13	184.59	185.20
C14	125.97
C15	143.16
C16	166.65
C17	166.79
C18	172.26
C19	150.36

Table 2. Computed and Available Experimental ¹H NMR Shifts for Folate.

atom no.	computed chemical shift (ppm)	experimental chemical shift (ppm)
H33	7.52	7.37
H34	7.39	7.37
H35	6.69	6.17
H36	6.51	6.17
H37	2.43	2.15
H38	2.07	2.05
H39	2.35	2.32
H40	2.57	2.32
H41	4.67	3.94
H42	4.66	3.94
H43	8.39	8.37
H44	4.34	4.27
H45	4.93
H46	4.92
H47	5.33
H48	6.29
H49	7.69
H50	8.14
H51	9.09

2.2. Ion Mobility Spectrometry

Collision cross section (CCS, units: Ų) is a gas-phase property of a molecule that is obtained using ion mobility spectrometry (IMS). In IMS, ionized molecules enter a drift tube or other ion conduit that contains an electric field to accelerate sample ions and a buffer gas to produce a countering drag force, resulting in separation based on the ion’s size, shape, mass, charge, conformational population, and interaction with the buffer gas.²⁴⁵ IMS is the gas-phase separation method analogous to liquid phase separation by electrophoresis, which also relies on molecular interactions with a buffer and electrical mobility to provide a force for acceleration toward a detector. Depending on the instrument, CCS can be calculated from the time taken to drift (as in drift time IMS) before detection (typically at a mass spectrometer) or via calibration against analytes with known CCS (as in traveling wave IMS). While IMS-MS techniques have been explored for nearly six decades, the use of CCS as a complementary property to mass and chromatography-derived retention time for identification of small molecules has only become popular, by way of instrument commercialization,²⁴⁶ in the past decade.²⁴⁵ IMS does not rely on condensed phase interactions that can be subject to degradation, contamination (e.g., heavy carryover), high variability, and difficult manufacturing requirements. Thus, measured CCS values can be very consistent over time and between laboratories, reaching relative standard deviations lower than 0.3%.²⁴⁷ Furthermore, because CCS is obtained after ionization, each analyte in the sample of interest can be represented by multiple adduct ions, a function of the analyte–matrix interaction, each with its own CCS and mass. As a result, observing multiple adduct ions lends additional evidence to the presence of a particular molecule.²⁴⁸

To better understand molecular ion behavior in ion mobility instruments, the prediction of CCS from molecular ion structures bourgeoned in the 1990s.^249,250 It was not until the early 2000s that researchers began to routinely use DFT methods to generate gas-phase molecular ion structures as a foundation for CCS calculations.^251−253 Currently, DFT-based calculations are considered the gold standard method in determining the adduct conformations that give rise to measured CCS; however, predicting CCS for use in small-molecule identification studies is quickly shifting to machine and deep learning methods (discussed in section 4.2) due to their speed and accuracy.^254−258 Typical procedures using DFT for CCS calculations include the prediction of the bonding structure of the ionized adduct (e.g., specific atom site of ionization), generation of a population of conformers of the adduct, optimization of conformer geometries, relative energy calculations for the conformers, CCS calculation for each conformer, and finally a method of either combining CCS values of conformers into a single combined CCS value for that conformational population (e.g., averaged or Boltzmann-weighted) or selecting a conformer that is most likely to represent an experimentally observed CCS peak. DFT is typically used for the geometry optimization and energy calculation steps, but it can also be used for ionization site predictions and the generation of conformer populations.

Some of the earliest examples of DFT use in CCS calculations for ion mobility experiments came out of Prof. Michael Bowers’ (University of California at Santa Barbara) and Prof. David Clemmer’s (Indiana University) groups. In a study by Wyttenbach, Witt, and Bowers, DFT calculations were used for a set of conformers (generated using the Assisted Model Building with Energy Refinement, or AMBER, molecular dynamics suite) of glycine, alanine, and their methyl-substituted derivatives.²⁵⁹ The study showed agreement between the predicted and observed CCS values, demonstrated the ability to determine likely conformations of the adducts and found differences in the adduct ion attachment (charge solvation, where the charge is stabilized by an electron dense region of the neutral molecule, and salt bridge, where the charge interacts with the zwitterionic form of the molecule).²⁵⁹ In a study by Leavell et al., diethylenetriamine–hexose complexes were investigated with CCS calculated using DFT-derived geometries.²⁵² Geometry optimization was performed using a low level of DFT theory along with a semiempirical method (AM1), with subsequent energy calculations performed at a higher level of theory. A small set of low energy candidate structures were found that match well to experimental CCS values, with evidence pointing to chair or twist-boat conformations for the hexose portion of the complexes.

While most early studies using DFT in CCS calculations focused on using these approaches to determine likely conformer structures of known molecules and complexes, it must be noted that even for low energy conformations, wildly different conformational structures can give rise to CCS values that are close enough to be experimentally indistinguishable with current instruments. Furthermore, CCS peaks of individual adducts can be much broader than the difference in peak max (center) CCS values between different molecules, reflecting the diverse conformational populations of ion packets. This issue becomes more pronounced with increased mass and decreased molecular rigidity (i.e., as degrees of freedom increase). Because most metabolomics studies using IMS operate at room temperature, adducts can rapidly interchange between conformations, as revealed by observed CCS peak distributions. Thus, we find the most value in DFT calculations for use in predicting CCS distributions to build identification libraries (i.e., to build evidence for identification of the underlying adduct) as opposed to determining the underlying conformer of an observed IMS peak. For determining specific conformations of gas-phase ions (especially when the molecule of interest is already known and purposefully being studied), we recommend cryogenic IR ion spectrometry,²⁶⁰ which is extremely sensitive to small changes in molecular conformation and provides tight constraints for calculations of molecular structures²⁶¹ (further details in section 2.3).

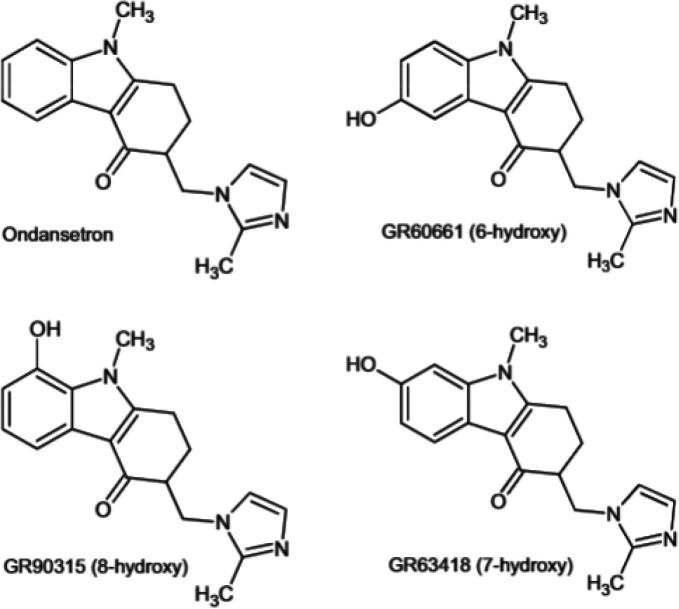
Through the pioneering work of Iain Campuzano and colleagues, the use of quantum chemical-based theoretical calculations of CCS for small molecule identification first appeared in the literature in 2010 (Figure 10).²⁶² In this work, the example molecules, isomeric hydroxylated metabolites of ondansetron, have indistinguishable MS/MS fragmentation spectra due to the hydroxyl moiety being located on the unfragmented benzene ring for all isomers. Thus, the matching of calculated CCS to the experimental CCS distributions was the sole distinguishing dimension of data for identification. Campuzano and colleagues quickly laid the foundation for use of DFT-based CCS calculations in small-molecule identification.^263,264 Recently, a high-performance computing (HPC)-friendly cheminformatics workflow, the in silico chemical library engine (ISiCLE), was created to automate all steps of DFT-based CCS calculations and uses software freely available to academics.²⁶⁵

Figure 10.

Drug ondansetron and the three hydroxylated metabolites identified in Dear et al. 2010.²⁶² This study was a first demonstration of the use of quantum chemical-based theoretical calculations of CCS for small-molecule identification. The four isomers had indistinguishable MS/MS fragmentation spectra due to the hydroxyl moiety being located on the unfragmented benzene ring, thus, the matching of calculated CCS to the experimental CCS distributions was the sole distinguishing dimension of data for identification. Reproduced with permission from ref (262). Copyright 2010 Wiley and Sons, Ltd.

2.3. Infrared Spectroscopy

IR spectroscopy has a long history of use in the identification of small molecules. During the past 30 years, hundreds of papers have described how IR spectroscopy techniques can be coupled to quantum chemical calculations like DFT to aid identification (via predicted resonance frequencies) and quantitation (via prediction of peak intensities). Like CCS, IR spectra can provide additional evidence for specific molecular structures, which may not be differentiated through traditional MS methods. For example, isobars, enantiomers, and other types of isomers may not always be separated using reversed-phase chromatography and may have identical MS/MS fragmentation spectra²⁶⁶ or even indistinguishable CCS. With rare exception, IR spectra are unique for every small molecule.²⁶⁷ Note that IR-vibrational circular dichroism (VCD) methods are required for determining the stereochemistry of chiral molecules. This approach, too, is amenable to DFT calculations that are accurate enough to determine absolute configuration.²⁶⁸

Martens et al. provided a thorough review of IR ion spectroscopy (IRIS) for small-molecule identification, including discussion of the history of IRIS for molecular identification, IRIS techniques, experimental advances, and applications in untargeted metabolomics.²⁶⁹ Furthermore, this review highlights the use of DFT, which can be both fast and accurate for gas-phase organic molecule ions, to support identification of unknowns without having a physical reference (i.e., standard) available. As an example, Martens et al. demonstrate the identification of a feature unidentifiable by LC-MS/MS, generated from samples taken from two siblings with a neurological disease of unknown etiology. IR spectra were calculated for candidate molecules obtained from a METLIN²⁷⁰ search, and the feature was identified as methyl-2-pyrrolidinone (an industrial solvent used in the production of polymers) by matching the measured IR spectra to a predicted spectrum (Figure 11).

Figure 11.

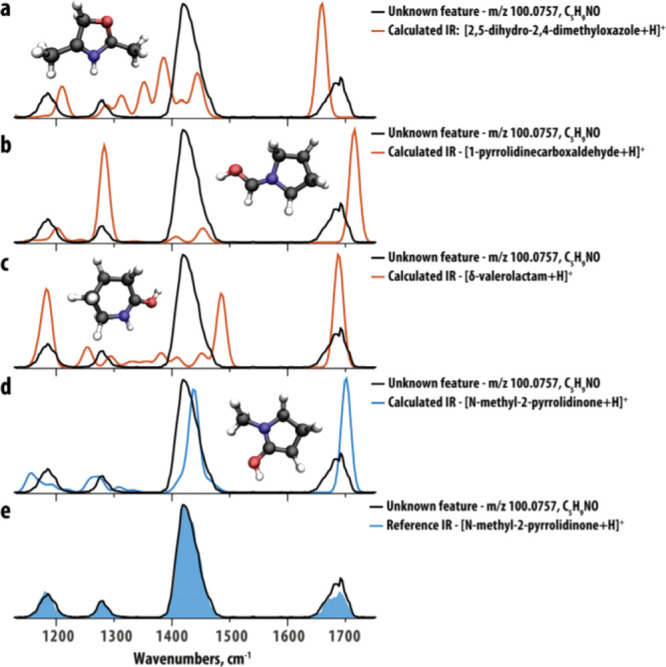
Computed IR spectra (colored traces, a–d) of potential candidate structures resulting from a database search for an unknown feature at m/z 100.0757 compared to the IRIS spectrum of the unknown feature (black trace) from the patient sample. (e) Compares the IR spectrum of the reference compound N-methyl-2-pyrrolidinone identified by the match found for the predicted spectrum. Reproduced with permission from ref (269). Copyright 2020 Elsevier.

Of significant importance to the small-molecule identification field is the recent advancement of cryogenic IRIS, spearheaded by groups at the Swiss Federal Institute of Technology Lausanne and University of Florida, led by Professors Thomas Rizzo^{260,261,271−276} and Nicolas Polfer,^277−281 respectively. If the ultimate goal of IR spectroscopy is to determine structural information on a molecule, the highest resolution (and highest deconvolution) can be obtained by reducing thermal inhomogeneous broadening and conformational heterogeneity.²⁶⁰ This can be done by cooling the ion packets (cryogenic cooling) and using conformational selection techniques (such as ion mobility). Cryogenic IRIS is sensitive to small changes in conformation, and when it is combined with a conformational filter such as IMS, both the measured CCS and IR spectra data are bolstered to provide overwhelming evidence for the presence of a molecule,²⁶¹ which can be confirmed through corresponding quantum chemical computations without relying on reference material. This is an emerging technology, and it remains to be seen how IMS, cryogenic IR spectroscopy, and quantum chemical calculations can be coupled for molecular identification to be performed in complex samples.

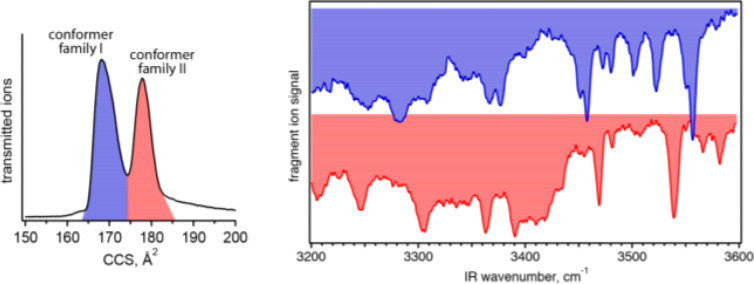
Some initial results on small molecules appear promising. As the only example that couples all three of these techniques to date, in 2018, Kamrath and Rizzo determined that the 178 Ų CCS conformer of the N-terminal fragment of bradykinin (RPPGF; [M + 2H]²⁺ adduct) was consistent with the trans-Pro²/trans-Pro³ isomer geometry (Figure 12).²⁶¹ This analysis relied on cryogenic IR spectra and DFT optimized molecular geometries. Interestingly, the trans-Pro²/trans-Pro³ isomer geometry is also that which is observed in solution via NMR and implies that the solution structure maintains its geometry during ESI. Other works without coupled ion mobility have also shown the value of quantum chemical calculations for molecular and conformer identification with the use of conformer-selective cryogenic IR spectroscopy.^275,281,282

Figure 12.

Ion mobility data (left) and cryogenic infrared vibrational spectra of individual conformer families of bradykinin [M + 2H]²⁺, consistent with the trans-Pro²/trans-Pro³ isomer geometry. Reproduced with permission from ref (261). Copyright 2018 American Chemical Society.

2.4. Mass Spectrometry

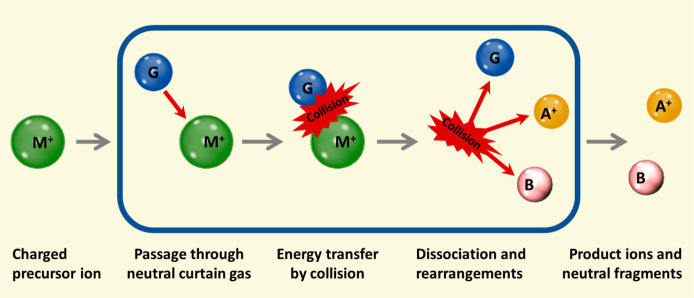
The main challenge of mass spectrometrists who are attempting to identify unknown compounds is in the interpretation of tandem mass spectra, thus the spectrum-to-structure approach (Figure 13). Quantum chemistry has had less impact on this subfield of MS when compared to spectroscopic methods such as IR, Raman, or NMR spectroscopy.²⁸³ For example, there are no completely quantum-chemistry-based computational pipelines that allow for truly unknown mass spectra to be analyzed, substructure assembled, and final structures proposed. Additionally, more complex approaches such as multiple-stage MS/MS exist (i.e., MSⁿ) that allow more intricate relationships between precursors and multiple product ions at different stages to be built.^284,285 So far, only cheminformatics, machine learning approaches,^286−288 or hybrid models have been able to perform successful spectrum-to-structure analysis.²⁸⁹

Figure 13.

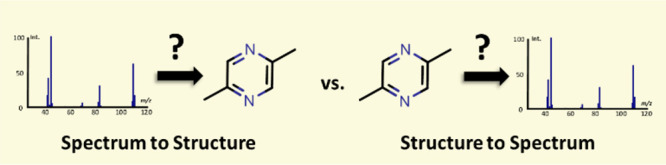
MS-based compound identification paradigm. Mass spectrometrists mostly deal with unknown mass spectra that need structural assignments (spectrum-to-structure). New algorithms to understand fragmentations need to be developed with the help of the quantum chemical community. Since the development of Grimme’s QCEIMS method in 2013,²⁹⁰ it is now possible to predict 70 eV mass spectra using Born–Oppenheimer ab initio molecular dynamics directly from structures (structure-to-spectrum). Large chemical databases with millions of compounds can be used to predict high-quality theoretical mass spectra.

The structure-to-spectrum approach is a very promising method for compound identification, because the number of known chemical structures far exceeds the current number of available experimental mass spectra (∼1 million).²⁹¹ Molecular databases such as ChemSpider and PubChem provide around 100 million compounds that could be used to calculate theoretical mass spectra based on quantum chemistry. It would then be possible to search unknown experimental spectra against vast libraries of theoretically predicted mass spectra.

In contrast to quantum-chemistry-based calculation of NMR, IR, UV, and Raman spectra, no straightforward procedure exists for quantum-chemistry-based prediction of mass spectra. For example, prediction of IR and Raman vibrational spectra became possible by 1965 using simple FFs²⁹² and in the late 1970s using ab initio calculations. While single fundamental fragmentations can be predicted with the help of quantum chemistry, the cascade of reactions and rearrangements resulting from multiple reaction pathways, and most importantly the m/z peak abundances from complex molecules, have been highly difficult to deduce.

In a major breakthrough and one of the most important discoveries in computational MS, Grimme published the Quantum Chemistry Electron Ionization MS (QCEIMS) program for the first principle calculation of 70 eV mass spectra in 2013.²⁹⁰ QCEIMS is discussed in more detail in section 2.4.1.

2.4.1. Electron Ionization (EI)

Electron ionization (EI) MS (70 eV) is an established analytical technique and is commonly coupled to GC for analysis of small molecules below 400 Da. Electrons are emitted from a heated filament and focused on gaseous neutral molecules. When the accelerated electrons hit the neutral molecule, radical cations are formed and another electron is ejected. The vibrationally excited carbocations then undergo further bond dissociations and fragmentations on a very fast time scale. The smaller mostly singly charged fragment ions are then accelerated toward a detector and recorded as spectral signals. The ionization efficiency at 70 eV is the highest, and most molecules can be ionized at this energy, allowing for creation of reproducible mass spectra.²⁹³ The power of GC-MS lies in the fact that the instrument industry has subsequently standardized the EI source energies to 70 eV, resulting in the availability of reproducible spectra and available databases to search.²⁹⁴ Gas chromatography coupled to tandem mass spectrometry (GC-MS/MS) has not reached a breakthrough yet due to the more complex instrumentation and missing MS/MS spectral databases for spectral matching.²⁹⁵

Historically, the interpretation of EI-derived spectra depended on statistical rate theory^296−300 and investigation of kinetic processes, especially work based on quasi-equilibrium theory (QET)³⁰¹ and Rice–Ramsperger–Kassel–Marcus (RRKM)^302−305 theory, which can be used to predict rate constants. Many of the classical investigations of 70 eV radical cations or anions are limited to single ion species or specific molecules due to the complexity of fragmentation and rearrangement reactions.

The main disadvantage of traditional QET/RRKM approaches is that rate calculations are based on the selection of specific ion transition states and activated complexes on the PES. With increasing atom numbers, the complexity of the reaction space rises exponentially and would require a priori knowledge of reaction pathways that are not always available.³⁰⁶ Methods such as the global reaction route mapping (GRRM) strategy,³⁰⁷ the AutoMeKin software³⁰⁸ or the Chemical Trajectory Analyzer (ChemTraYzer) software³⁰⁹ have been developed to systematically and automatically explore the reaction space.¹⁵⁹

The QCEIMS approach published by Grimme in 2013 combines Born–Oppenheimer molecular dynamics (BOMD), a type of AIMD, with statistical sampling to predict 70 eV mass spectra.²⁹⁰ In contrast to other methods, QCEIMS is purely based on physical and chemical principles and can calculate mass spectra from any given molecule. Using a combination of ab initio molecular dynamics (AIMD) and stochastic sampling across hundreds of reaction pathways, the correct m/z value of ions and their associated abundances can be predicted. More excitingly, all reaction trajectories are retained and allow for a “look inside” the reaction processes of a mass spectrometer, which then makes it possible to investigate all fragmentations and rearrangements individually. To achieve a balance between efficiency and accuracy, QCEIMS can calculate on various levels of theory, including semiempirical models OM2/OM3,³¹⁰ DFTB+,³¹¹ GFNn-xTB,³¹² and several DFT methods. The complex relaxation processes from the electronically excited state of the precursor ion are modeled by limiting the reaction on ionic ground-state PES. The impact excess energy is converted to kinetic energy by a heating process, during which the atomic velocities are scaled to a preset impact excess energy value. Such a simple electronic structure can handle the fragmentation reactions and its ability to give a reasonable result is one of the key innovations of QCEIMS.²⁹⁰

The QCEIMS software is coupled with several independent software packages such as ORCA,^313,314 TurboMole,³¹⁵ MOPAC,³¹⁶ MNDO99,^317,318 and DFTB+.³¹¹ Most importantly, the latest independent and therefore stand-alone version of QCEIMS directly implements the GFN-XTB method. This allows for simple installation and practical use of QCEIMS in any research environment with access to HPC. The only required input is a chemical structure. Because the GFNn-xTB³¹² methods are parametrized to elements up to Z = 86, they are applicable to the most common molecules and therefore provide calculations of 70 eV mass spectra with metalloids such as silicone.^319,320 This is important because the trimethylsilyl group (TMS) is often used during GC-MS derivatization experiments.³²¹

One of the advantages of QCEIMS is that reaction pathways are automatically recorded as MD trajectories during the simulation. This allows for comprehensive investigation of the fragmentation mechanism. However, the confirmation of such reactions would require comprehensive investigations because, for any given reaction, a multitude of possibilities exists. In the original paper,²⁹⁰ Grimme found that most of the primary fragmentations occur within 2–3 ps, while secondary fragmentation reactions take much longer but are important in larger systems. Many well-known reaction pathways in MS are accurately reported by QCEIMS, including α-cleavage,³⁰⁶ McLafferty rearrangement, retro-Diels–Alder³²² reaction, and CO loss.²⁹⁰ For molecules with several tautomers, a combination of initial conditions based on Boltzmann population can be used to improve simulation accuracy.³²²

In 2016, Cautereels et al. described a different method for the calculation of 70 eV mass spectra using empirical rules for limiting the number of fragmentations along the PES based on DFT calculations.³²³ The rules include observations of bond strengths, bond cleavages (that are thermodynamically controlled), and 1,4-rearrangements and McLafferty rearrangements (that are kinetically controlled).³²⁴ The procedure includes conformational sampling and calculation of Boltzmann weights including the calculation of the most stable radical cations. Homolytic and heterolytic fragmentation pathways are calculated under observation of the heuristic rules. Final peak abundances are determined based on a formula that includes the average of energies of the fragmentation pathways and specific fragments. Such an approach could become very useful in the future for detailed investigations of reaction pathways using classical transition state theory.

Similar to the evaluation of machine-learning prediction methods such as CFM-ID,³²⁵ quantum chemical models have to be rigorously tested by comparing theoretical predictions against experimental reference spectra.³²⁶ Similarity match scores and compound rankings should be reported.²⁹⁴ This can be done with the National Institute of Standards and Technology (NIST) MS Search program and the NIST and MassBank of North America (MoNA) mass spectral databases.²⁹⁵

2.4.2. QCEIMS Computational Costs and Accuracy

The QCEIMS protocol contains three types of quantum mechanical calculations: energy/force calculations to generate the potential energy surface for MD, molecular orbital (MO) calculations to determine internal excess energies, and ionization potential (IP) calculations of each fragment to generate the statistical charges. The original version of QCEIMS utilizes DFT methods for MO and IP calculations, whereas the energy/force calculations for the time-consuming MD steps use the OM2/OM3³²⁷ orthogonal corrected semiempirical methods.

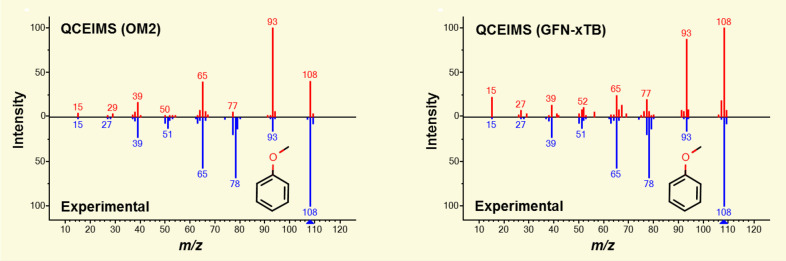
For example, the simulation of the 70 eV EI mass spectrum of anisole (C₇H₈O, MW = 108.057 Da) (Figure 14) requires 1.2 million individual MD steps and 82 min of computational time on 16 CPU cores at the OM2 level. The choice of the underlying method significantly affects simulation speed. The GFNn-xTB methods^319,320 will be 10–20 times slower than the semiempirical OM2³¹⁰ simulations, while purely DFT-based MD can be 100 or more times slower than the semiempirical methods.

Figure 14.

The 70 eV mass spectra of anisole calculated with QCEIMS. (left) The in silico spectrum calculated with the OM2 semiempirical function, while (right) shows the GFN1-xTB Hamiltonian. Both algorithms underestimate the peak at m/z 78 and overestimate the peak at m/z 93. This leads to a similarity score of 569 for OM2 and a somewhat higher match score of 660 for the new GFN1-xTB method. Further methodic improvements have to be made to increase the quality of the simulated spectra.

The computational cost for semiempirical methods is usually much smaller than ab initio methods (OM2/PM6³²⁸ < GFNn-xTB < DFT), whereas in terms of accuracy, we see the opposite trend with DFT being the most accurate method (DFT > GFNn-xTB > OMx/PMx). Interestingly, chemical bonds are more easily dissociated in semiempirical simulations relative to the more accurate DFT simulations.³²⁹ Therefore, more accurate calculations of the PES may require even more simulation steps with longer fragmentation processes. While semiempirical methods like OM2/OM3 are significantly faster than GFNn-xTB, the PES along bond dissociation coordinates are not sufficiently accurate, leading to simulated spectra that have lower similarity scores when compared to experimental reference spectra (Figure 14).

Because DFT methods are closer to the “exact” PES, they should be used as a reference in evaluating more approximate models,³²⁹ but their increased computational cost puts them out of reach for simulating EI mass spectra of larger molecules. We are optimistic that GPU-accelerated implementations of DFT methods in software such as TeraChem^87,330 or Fermions++ may lead to fast high-accuracy simulations.³³¹

However, the usage of fractional occupation number weighted densities³³² can reproduce some properties of multireference wave functions, making it a possible low-cost alternative for treating multireference systems. On the other hand, when the energy gap between the excited state and ground state goes to zero, the Born–Oppenheimer approximation and single reference methods used in QCEIMS can break down. The treatment of highly excited electronic states using multireference methods,⁹⁶⁻⁹⁸ such as the states accessed during QCEIMS, is under active investigation and can guide the development of improved simulation approaches in the future.

The accuracy of predicted in silico spectra has to be evaluated against diverse and large number of experimentally measured spectra.²⁹⁴ QCEIMS (with OM2/OM3) performs on the same accuracy level as the best available machine learning algorithms such as CFM-ID.³²⁵ The QCEIMS method also has the advantage that any given molecule can be calculated. The reason is that machine learning methods require experimental training data, while QCEIMS as an ab initio method is only based on physical and chemical principles. The most important question for practitioners is the practical use of algorithms in daily research applications. Currently, it is not possible to calculate most compounds with high similarity match scores (>850). It is also not yet possible to determine the quality of predictions in advance due to the stochastic nature of the computations. It is foreseeable that with improved accuracy of future versions of QCEIMS and related methods, a wide range of in silico spectra can be used for training in machine leaning to allow for even faster simulation of in silico mass spectra from all known compounds.

2.4.3. Coupling EI to Other Spectroscopic Methods

While GC-MS mass spectra at 70 eV can give structural insights, it is not possible to fully interpret all mass spectra because in many cases the molecular ion is not observed and following individual fragmentations is not directly possible. Techniques such as chemical ionization or cold EI can help increase the stability and abundance of the molecular ion.³³³ Furthermore, integrating parallel analysis techniques such as IR, Raman, and UV will allow for easier structure-to-spectrum identification using quantum mechanical calculations of optical spectra.³³⁴ In such a case, MS and optical spectroscopy experiments are performed in parallel, and the resulting spectra can be investigated theoretically using quantum chemistry methods or QM/MM.³³⁵ For example, threshold photoionization mass spectra can be acquired with photoelectron photoion coincidence (PEPICO) spectroscopy and can be coupled with DFT calculations to gain insights into fragmentation behavior.^336−338 In particular, coupling MS with IR multiple-photon dissociation spectroscopy (IRMPD) seems to be an excellent way for interpreting dissociation pathways by combining experiments with quantum chemical calculations.³³⁷ While such instrumental setups are complex and expensive, they show the possibilities of instrumental integration with quantum mechanical computations. Such techniques, while discussed here in detail for EI, can also be coupled to other methods such as ESI and CID MS/MS.

2.4.4. Collision-Induced Dissociation

Tandem mass spectrometry (MS/MS) uses one or more mass analyzers paired with a fragmentation technique that activates and dissociates ions to identify structural information. The tandem-in-time concept describes fragmentation processes in ion trap and Fourier transform ion cyclotron resonance (FT-ICR) mass spectrometry instrumentation, whereas the tandem-in-space describes fragmentations in triple-quadrupole (QQQ), quadrupole-time-of-flight (Q-TOF), and hybrid instruments.³³⁹ The MS/MS approach is commonly applied to compound identification in mixtures. In this procedure, a soft ionization method such as ESI is generally used in the first stage to generate nearly intact molecular ions from the sample, which are selected by mass in the first mass analyzer. These ions are then fragmented via ion activation processes, followed by subsequent mass analysis to determine their structural composition. While many other ion activation modes such as surface-induced dissociation or in-source fragmentation exist,³³⁰ only the most prominent fragmentation method, CID, also sometimes called collision-activation decomposition (CAD), is discussed here.

CID was introduced by the Jennings and McLafferty groups in 1968 as a tool to identify the structures of molecular ions.^340,341 During the 1970s, CID-MS/MS was made commercially available in a form of sector-MS/MS, and later triple quadrupole mass spectrometers were developed by Yost and Enke.^342,343 Initially, most experiments were performed using high collision energies in the keV range, but today, instrumentation operating in that regime is only used for very specific research purposes.

In the 1980s, lower energy CID-MS/MS with collision energies in the 1–100 eV range was introduced by Douglas and Dawson.^344−346 The majority of today’s commercial mass analyzers operate in the low energy CID mode. The most common instrumental setups for untargeted profiling of complex biological samples include ultraperformance LC coupled to orbital ion trap tandem mass spectrometers (Orbitrap) or quadrupole-time-of-flight instruments (Q-TOF). Compound identification for small molecules mostly relies on database search of low-energy CID-MS/MS spectra²⁹⁵ or HCD (higher-energy collision dissociation)-MS/MS spectra from orbital ion traps.

Currently available MS/MS databases are rather small, with fewer than 500 000 covered compounds, and metabolic profiling reports still contain many unknown MS/MS spectra.³⁴⁷ Therefore, a major research topic is the modeling of high-quality CID-MS/MS in silico mass spectra directly from compound structures (structure-to-spectrum approach). The spectral interpretations can provide a better understanding of the CID fragmentation pathways in unknown CID-MS/MS spectra (spectrum-to-structure approach).

The CID process can be distinguished into different types: collision-cell CID, ion trap-CID, and in-source CID.³⁴⁸ During the collision-cell CID process, ions pass through the collision cell, a vacuum chamber that is flooded with inert gas such as helium, nitrogen, or argon, where binary collisions occur in the gas phase (Figure 15). The collisions within the cell increase the internal energy of the ions and enhance the rate of the unimolecular fragmentation reactions that create the product ions. If the amount of energy transfer is great enough to break chemical bonds, the ion consequently decomposes into charged ions and neutral fragments. In the case of collision-cell CID, an ion makes approximately 10 collisions on average while traveling through the collision cell within 20 μs; as many as 100 collisions are possible in ion-trap CID over the corresponding residence time of ∼5 ms.^349,350

Figure 15.

Collision-induced dissociation process (CID-MS/MS) in a collision cell. Ions formed by, e.g., electrospray ionization enter the mass spectrometer and pass a neutral curtain gas (He, Ne, Ar). Once energy is transferred from the collision, molecules can dissociate or rearrange. Ions are further accelerated toward the detectors and registered as specific m/z signals. The collision gas and neutral reaction products are removed by the vacuum pumps of the instrument.

Although the entire CID process occurs on time-scales that are inaccessible by ab initio or even semiempirical MD methods, it may be possible to use simplified models to approximate the kinetic energy that is imparted by nondissociative collisions that lead up to the dissociative event, in a similar way to how QCEIMS uses a velocity rescaling to model the complex energy conversion process from an electronic excited state to nuclear kinetic energy. Like the case of EI-MS, there are many possible pathways for collisional activation and fragmentations across the diverse configurations of CID experiments and instrument configurations. Many of them should be considered during quantum chemical investigations.

2.4.5. Interpretation of CID-MS/MS

The CID-MS/MS process includes many different fragmentation and rearrangement reactions, divided into charge retention and charge migration mechanisms.^351,352 For quantum-chemistry-based CID-MS/MS investigations, one can distinguish between statistical and dynamical models. Specifically, (i) transition state theory and simulations along the PES and (ii) molecular dynamics (QM/MM) simulations.^353−356

Semiempirical and DFT models have been used in the past on a number of molecular species to understand CID-MS/MS dissociations.^357−359 For example, the number of bond cleavages and proton migration events were determined by semiempirical methods.³⁶⁰ The QC-FPT method was used to predict thermodynamically feasible fragmentations across a number of sample molecules.³⁶¹

The VENUS software, developed by the Hase group at Texas Tech University, has been extensively used to model CID MD processes. VENUS has been interfaced with software tools for semiempirical (MOPAC)³⁶² and DFT calculations (NWChem).³⁶³ Several papers also have shown that MD simulations can be coupled to the automated reaction mechanisms and kinetics software AutoMeKin/TSSCDS, which automatically explores transition states.^308,364,365 Because of the time-consuming nature of the approach, mostly single molecules such as sugars, sterols, amino acids, and peptides have been described.^365−371

A QM/MM direct dynamics simulation described in a recent paper further details the modeling of center-of-mass collisions of argon and galactose-6-sulfate.³⁷² The reaction process can be visually investigated, including collisions and formation of multiple fragments. This computational process with improved statistical sampling can be considered as a foundation for simulations of CID-MS/MS spectra. Further details of the historical developments and implementations of QM/MM methods are comprehensively described in the excellent book by Song and Spezia.³⁷³

2.4.6. Prediction of in Silico CID MS/MS Spectra

As of 2020, no commercially or publicly available quantum chemistry method exists with the ability to accurately predict CID-MS/MS spectra from diverse compounds (<1000 Da). While several heuristic, machine learning, and reaction-based models can accurately model CID-MS/MS spectra for small molecules, they usually require experimental training spectra and are discussed elsewhere.²⁸⁸

Similar to CID fragmentation predictions, classical reaction mechanism theory as well as QM/MM calculations including AIMD can be used to predict ions and their abundances. The QCMS² approach uses a pipeline of conformational sampling, protonation, fragmentation rules, and exploration of transition states along the PES.^374,375 Formerly developed for EI-MS, it has been modified to work for CID predictions.³⁷⁶

A QM/MM chemical dynamics approach, using the VENUS chemical dynamics software and semiempirical and DFT calculations, was able to predict fragments and relative peak abundances of testosterone.³⁶⁶ Another workflow used an automatic tautomerization network and was subsequently able to describe a mobile proton model during the fragmentation of 6-O-methylguanine.³⁷⁷ Fragments and relative abundances were calculated and compared to experimental Orbitrap HCD-MS/MS spectra. Several efforts have been made to predict CID-MS/MS spectra for specific target compounds, mostly with constraints on compound diversity or the experimental setup.³⁷³

While fragmentations may be easily predicted,^357,358,378 the prediction of ions with a low false-positive rate and accurate prediction of associated ion abundances are still very challenging.³⁶⁶ In addition, many other aspects of automatic CID-MS/MS modeling workflow need to be considered, such as correct sampling of protomer, rotamer, and conformer samplings, as well as energy distribution and transfer upon collision with various collisional energy.^361,379 Some of these challenges are further discussed below.

Adduct formationis of high interest for mass spectrometrists because a multitude of adduct ions such as [M + Na]⁺, [M – H]⁻, or [M + Cl]⁻ are observed during experiments.^380,381 Depending on the ionization mode, solvent, and buffer systems, different ions are formed during the electrospray process^295,382,383 that can strongly influence the MS/MS fragmentation process and observed product.^295,384,385 A statistical analysis of the NIST database on 80 000 MS/MS spectra covering 300 possible adduct species showed that protonation [M + H]⁺ and deprotonation [M – H]⁻ are the most commonly observed adducts in ESI. Doubly or higher charged species are rarely observed in small molecule MS/MS spectra, but they are very important in proteomics and peptide sequencing.^386,387

Multiple protomer species must be considered in the cases of complex molecules with diverse ionizable groups.^388−390 The selected computational approach must be able to model intramolecular proton migrations.³⁹¹ While the best practice currently is to calculate protomer ensembles using a Boltzmann distribution,³⁵⁷ experimental investigations have shown that the observed protomer species might not always be the thermodynamically favored species.³⁹² The freely available Conformer–Rotamer Ensemble Sampling Tool (CREST), a conformer-rotamer ensemble sampling tool based on the GFN-xTB method, can automatically enumerate and compute energies of multiple protonation states.^379,393 The included ensemble sorting tool (CREGEN) then performs a Boltzmann population analysis and ensemble analysis. While all of these computations are based on the semiempirical GFN-xTB level.³⁹⁴ Orthogonal techniques such as ion mobility spectrometry (IMS) can help to understand multiple protonation sites.³⁹⁵

The modeling of tautomers can also be challenging.³⁹⁶ While tautomers have been observed in many mass spectrometric experiments,^397−400 the formation process is solvent- and pH-dependent and not fully understood yet.^377,401,402 However, tautomers can be easily enumerated with commercial and open cheminformatics tools such as ChemAxon, OpenEye, RDKit, MolTPC, CDK, or AMBIT.^403−406 A fully automatic generation of tautomers using solvation models and quantum chemistry approaches is possible with CREST and the XTB software.^394,402

The influence of conformer ensembles, rotamers, and stereoisomers is important for predictions across many spectroscopic methods. However, MS alone is rarely used as standalone technology to analyze rotamers or stereoisomers because additional orthogonal separation technologies such as GC, LC, or ion mobility allow for better resolution.⁴⁰⁷ The consideration of multiple conformers is important for CID modeling. The existing software for generation of conformer ensembles for NMR spectral predictions could be used and integrated into CID modeling workflows.^210,408 The freely available XTB, CREST, and ENSO software modules are an excellent starting point to perform such analysis.³⁹³

The difficulties of modeling CID-MS/MS spectra are based on a number of factors, including diverse instrumental setups,⁴⁰⁹ different ion activation schemas, and CID-voltage dependent fragmentations.⁴¹⁰ Also, the time-scale of fragmentations are important. Whereas CID collisions are modeled in the picosecond to femtosecond range, the experimental time-scale can last up to milliseconds in certain instruments such as FT-ICR MS.^378,411 Modeling a single collision might not be sufficient because multiple collision events may occur depending on instrument type.^411,412

The developmental focus for the structure-to-spectrum approach should be on modeling low-energy CID-MS/MS spectra that match the most commonly used instrument types. That includes QTOF-type (CID-MS/MS) and Orbitrap-type (HCD-MS/MS) instrumentation for the small-molecule communities.^413,414 Modeled in silico spectra must contain accurate m/z values and associated peak abundances. The quality of prediction needs to be reported by matching theoretical MS/MS spectra against experimental reference spectra visualized in head-to-tail view, using cosine, dot-product, or other mass spectral match scores.²⁹⁵ There are many public and commercial MS/MS databases, including MoNA, NIST, METLIN, and mzCloud, that can be used to obtain experimental reference MS/MS spectra.²⁹¹ The publication of opaque approaches should be avoided, describing methods or software that are neither commercially nor freely available. In silico spectra should be made publicly available in electronic (MSP/MGF) format.^295,415

Overall, methods for accurate prediction of CID-MS/MS spectra by quantum chemistry approaches are still in their infancy. However, current advances for de novo prediction of MS/MS spectra made by multiple groups worldwide are very promising, and the topic itself is currently gaining attention within the quantum chemistry community. Looking even further into the future, quantum computers will be able to solve quantum chemistry problems⁴¹⁶ and predict molecular spectra⁴¹⁷ at an unprecedented speed and scale. Theoretical frameworks must be developed and linked to perform confident spectrum-to-structure and structure-to-spectrum predictions in the realm of MS to take advantage of this advance.

3. Current Best Practices and Known Sources of Error

3.1. Basic Procedures and Implementation Methods

3.1.1. Containerization and Cloud Computing

Traditionally, quantum chemists use local HPC resources, including compute clusters and local data storage. Considering cloud resources, one should carefully consider a number of aspects: computing costs, data storage, and data transfer, such as egress costs (moving data out of the cloud).⁴¹⁸ This could result in substantial charges in cloud computing that have to be covered by a research budget, whereas local computing is mostly provided for free or is covered by low-cost contributions. The NIH Science and Technology Research Infrastructure for Discovery, Experimentation, and Sustainability (STRIDES) Initiative is actively investigating cloud storage and cloud computing with two major partners, Google Cloud and Amazon Web Services (AWS). The aim is to use cost-. and industry-leading commercial resources to advance biomedical research (datascience.nih.gov/strides).

There are many advantages to using commercial cloud services. Microservices and serverless computations (AWS lambda) and easy containerization using Docker or Singularity allow for quick deployments.^419,420 Furthermore, horizontal scaling to thousands of instances is easily possible on the cloud, while local HPC clusters usually have limitations in available on-demand compute capabilities. Customizing CPU and memory use and the use of preemptible instances can greatly reduce the costs.

While local HPC centers have administrative staff and programmers, when using cloud services, the user in many cases also becomes the systems administrator. This can be initially problematic when setting up scheduling systems such as Torque PBS or Slurm or the need for setting up complex networks or cloud data-storage solutions. Finally, licensing requirements must be cleared with commercial software providers when hundreds or thousands of instances are deployed or software is limited in terms of CPU sockets in use. Here the use of open-source quantum chemistry software, such as Psi4⁸² and NWChem,⁸⁴ can be recommended with no distribution or licensing restrictions.

3.2. Sources of Error and Methods of Correction

The models we use to represent the world are not perfect; however, quantum chemistry has come a long way in being able to accurately reproduce many aspects of the natural world. Even so, errors persist. Below, major sources of errors computational chemists face when performing quantum mechanical calculations are addressed. For additional in-depth discussions on errors in theoretical calculations on small molecules, see the following references (^{135,231,421−423}).

3.2.1. Level of Theory

In general, the accuracy of quantum mechanical calculations improves as the cost (measured, generally, in terms of computational time) of the calculations increases. To obtain accurate results without excessive computational cost, DFT is generally recommended, as opposed to less accurate but faster levels of theory, such as HF,^424,425 or generally more accurate but time-consuming levels of theory, such as CCSD.^{135,231,421,422,426−431} Goerigk and co-workers, in both their 2017 and 2019 reviews of “the density functional theory zoo,” stress the importance of including dispersion corrections, such as D3(BJ) and suggest using double-hybrid functionals.^135,421 However, depending on the specific research questions to be addressed and the acceptable error bars that can be tolerated, the well-worn and too often maligned B3LYP method is often sufficient.^{231,427,432−434}

3.2.1.1. Solvent Effects

Solvation can be represented both implicitly (with a field) and explicitly (with discrete solvent molecules included in the calculations). Implicit solvation is a good starting point because it is much less computationally demanding than explicit solvation modeling and is frequently sufficient to calculate desired properties. Explicit solvation should always be considered, however, if strong intermolecular interactions are involved, e.g., traditional H-bonding, CH–X, cation−π etc.(231,435) For example, Da Silva et al. found including four explicit chloroform molecules along with an implicit chloroform model afforded more accurate ¹H chemical shifts than with the implicit solvent model alone.⁴³⁵ This is but one representative example.

3.2.1.2. Questions of Dimerization, Acidity/Basicity, Heavy-Atom Effects, and Hybridization

The best approach to modeling the solute is often nontrivial, for example: (i) if a compound of interest exists as a dimer in solution and must be modeled as such to reduce error,⁴³⁷ (ii) if the protonation state of a compound is difficult to predict and multiple protonation states must be modeled,⁴³⁶ (iii) if the effects of intramolecular noncovalent interactions on a particular property are overestimated in the calculations an error that potentially can be reduced through randomly averaging out free energies of the conformers as recommended recently by Sarotti and co-workers,⁴³⁸ or (iv) if the properties of individual atoms, such as labile protons (Figure 16) or atoms next to heavy atoms, which suffer from relativistic effects, require specialized methods.^231,439 For example, Kutateladze and Reddy were able to reduce this latter error by accounting for spin–orbit effects by developing the DU8+ method to predict accurate ¹³C chemical shifts for ¹³C–X carbons. With this technique, they were able to correct the structures of numerous natural products with the misassigned configurations or halogen positions, as in the case of tristichone C (Figure 17).⁴³⁹ Another method used to account for errors specific to atom types is the multistandard approach that has been used to reference different ¹³C or ¹H chemical shifts based on the hybridization of the carbon atom.^440,441 Overall, the more accurately a chemist can model what is occurring in the physical sample that is measured, the more accurately they will be able to predict the chemical properties of their system. Determining what is occurring in a sample from the empirical data, however, generally relies on the chemical intuition of the analyst.

Figure 16.

Effects of a labile carboxylic acid proton on ¹H and ¹³C chemicals shifts.⁴³⁶ Reproduced with permission from MDPI (2017, CC-BY 4.0 license).

Figure 17.

Structural reassignment of the natural product, tristichone C by Kutateladze and Reddy using their DU8+ method.⁴³⁹ Reprinted with permission from ref (439). Copyright 2017 American Chemical Society.

3.2.1.3. Conformational Searching

Conformational space increases rapidly with degrees of freedom in small molecules, and as such, determining all relevant conformers becomes increasingly difficult as the number of atoms increases.⁴³⁴ Often, errors are particular to the software and/or conformer generation algorithms used. Traditional approaches, including the use of simulated annealing^442,443 or brute force sampling methods,⁴⁴⁴ can introduce errors because these are generally carried out using nonquantum mechanics methods.⁴⁴⁵ For example, when searching for conformers of strained rings with some methods, only conformers with the same dihedral angle sign as the original input structure will be found in the conformational search.⁴⁴⁶ A new conformational searching method created by Grimme et al., CREST, provides a fast alternative method that addresses this and other errors found in traditional conformational searching methods.^210,445,447 This method, while it does not always provide the most accurate conformer population, often provides adequate sampling of the conformational space and is freely available on Github.

3.2.1.4. Energy Calculations

Calculating accurate relative free energies of unique conformations is important to correctly predict most properties of small molecules because small differences in free energy correspond to large differences in observed conformational populations (ΔG = −RT ln K)^438,448 and, by extension, the property of interest. Although DFT is often used to calculate a variety of chemical properties, Bootsma and Wheeler recently brought to light the problem that the orientation of an initial molecular structure for an optimization calculation can drastically affect the resulting free energy of that compound if the integration grid (i.e., the number of points sampled) used is too small. With a large enough grid size (e.g., 99 590 or greater), this error can be reduced to 1 kcal/mol or less,^449,450 so using such a grid is suggested for quantum chemical calculations in general.^{407,408,427,449,450}

3.2.1.5. Boltzmann Averaging, Conformational Weighting, Conformational Analysis

When performing conformational analysis, depending on the chemical system and properties of interest, a single low energy conformer may be all that is required to arrive at accurate predictions. For more flexible systems, Boltzmann averaging is commonly used to combine per-conformer properties based on the relative populations of these conformers. This approach involves giving a weight to the properties for each conformer with relative free energies within ∼3 kcal/mol of the lowest energy conformer (for room temperature calculations).²³¹ However, the errors in the free energy calculations for each conformer, which are affected by the level of theory, temperature, and solvent model used, can be large enough to significantly affect properties predicted based on this weighting.^{135,238,451,452} Consequently, alternative methods are becoming increasingly employed, such as the Computer Aided Structure Elucidation-3D (CASE-3D) method or the random ensemble method.^438,448

3.2.2. Sources of Error Specific to Techniques

3.2.2.1. NMR

Computational prediction of NMR chemical shifts and coupling constants has become an invaluable tool for the structure elucidation of natural products.^{231,432−435,453−456}

Linear Regression: Simply referencing chemical shifts to a single standard (e.g., TMS for organic, nonpolar, solvated samples; sodium trimethylsilylpropanesulfonate, i.e., DSS, for water or polar solvated samples) can introduce inaccuracies, so linear scaling factors are often used instead to convert isotropic shielding constants to chemical shifts.²³¹ Scaling factors for ¹H and ¹³C,^{231,235,238,45711}B,⁴⁵⁸¹⁵N,⁴⁵⁸¹⁹F,⁴⁵⁹³¹P,⁴⁶⁰¹³C–X,⁴³⁹ and ¹H–¹H J-couplings⁴⁶¹ are available to reduce systematic error. Many scaling factors and instructions on how to use them are freely available on the CHESHIRE (CHEmical SHIft REpository) Web site (cheshirenmr.info).²³¹ While linear regression allows for accurate scaling in most cases, the multistandard approach or the use of secondary linear regression lines can be used to improve accuracy for specific types of atoms.^238,440,441

3.2.2.2. pH Effects on Chemical Shifts

pH of the NMR solution also can affect chemical shifts.^435,462,463 How best to model a compound when this is an issue is unclear, although improved predictions have been made by explicitly modeling solvent or acid molecules.^435,462,463

3.2.2.3. IR/Raman

In IR calculations, anharmonicity can introduce a significant source of error depending on how it is calculated (if at all). The generalized second-order vibrational perturbation theory (GVPT2) is recommended and often used to reduce the effects of Fermi resonances resulting from anharmonicity if highly accurate IR spectra are needed.^427,437

3.2.2.4. CD

Circular dichroism is again dependent on correct conformational analysis.^434,452,464 In addition, as for NMR, a scaling approach can be applied, here using a wavelength correction.⁴³⁴

3.2.3. Limitations and Challenges

As far as quantum mechanical calculations have come in recent years for structure elucidation and small molecule identification, they are limited by the quality of the experimental data obtained for metabolomics studies. Thus, a movement has been made toward including raw data and error bars in publications to allow for better analysis and comparison of scientific data.^423,465 Even with excellent experimental data, the computational chemist is limited by time and resources. With the technology currently available, cyclopeptides with five or so residues represent a practical size limit for accurate DFT-based computations.^466−470

Other than size, strong inter- or intramolecular interactions, both charged and uncharged, can create challenges in producing accurate theoretical results. Even the seemingly simple question of protonation/deprotonation is often complicated to model appropriately.⁴³⁶ Because of these factors and the time involved in DFT calculations, automated structure elucidation with NMR spectroscopy is gaining popularity and can be a good starting point for metabolite identification, although it is recommended to confirm the results with quantum chemical calculations. Some popular methods include CASE,^471−473 WebCocon,^474,475 and Logic for Structure Determination (LSD).⁴⁷⁶

3.3. Validation Methods

3.3.1. Statistical Verification with Large Data Sets

Statistical verification for quantum chemical calculations is becoming increasingly popular for DFT calculations of energy. While optimizations performed at efficient levels of theory can provide accurate conformational minima, they often have difficulties accurately predicting relative free energies. Including a statistical component, as with the DP4/DP4+ and related methods, allows one to assess the likelihood of a specific structural assignment being the correct one out of a group of defined possible structures;^228,467 however, it should be noted the DP4+ method does not always suggest the correct stereochemical assignment.⁴⁵⁶

A recently published method, the In Silico Chemical Library Engine (ISiCLE),²⁶⁵ has shown promise in structure determination using NMR, IR, and CCS predictions and has performed well in large-scale compound identification tests, such as the ENTACT interlaboratory challenge.²⁴⁸ This method, which can be used as a cross-validation method, aims to provide a means for structure prediction without standards, a major advantage to rapidly accelerating compound identification.²⁶⁵

3.3.2. Cross Validation

Cross validation with multiple methods can help one avoid errors. For example, comparing results from Boltzmann averaging with Sarotti’s recently introduced random ensemble method can reduce errors.⁴³⁸ Scaling factors are generally cross-validated with a second set of compounds after they are calculated from a test set.²³¹ In the long run, “consensus scoring,” which is frequently done in fields like automated ligand docking, may have an important role to play in compound identification.

4. Outlook for Role in Metabolomics

4.1. Advancing Standards-Free Metabolomics

Most metabolomics studies use databases with known experimental MS or NMR data obtained from analyses of standard compounds. Such databases are useful but do not go beyond known metabolites. The problem is that a very large number of metabolites are not represented in databases. Identification of such unknowns requires considerable experimental effort using approaches employed in natural products chemistry.⁶⁰ Furthermore, the number of purified or synthesized chemicals that are available for traditional database construction will always be a limitation. We believe that computational methods, most specifically those based in quantum mechanical calculations (and eventually coupled to deep learning and quantum computing approaches), can provide considerable help in the identification of unknown compounds.

Using high-level calculations like those outlined in this perspective, QM calculations could be accurate substitutes for experimental data. In fact, QM is a hallmark for high confidence spectroscopic (and spectrometric) simulations, and it has been proved to produce reliable results enabling structure confirmation,^477,478 distinction between isomers,⁴⁷⁹ and to point out wrong assignments from peer-reviewed publications.^480,481 One advantage of using QM calculations for database entries is that they can be applied to several experimentally accessible measurements including retention time, MS/MS fragmentation, collisional cross section, and NMR data. One rapidly growing application area that has yet to incorporate standards-free and QM calculation-based identification methods is metabolomics imaging. MS imaging, specifically, has historically utilized m/z features alone for putative identifications, but as MS/MS and IMS are increasingly incorporated into these analyses,^482−487in silico libraries may help to accelerate the usefulness and impact of metabolomics imaging research by providing high confident metabolite identifications.

For NMR data, most experimental databases rely on chemical shift values, but other experimental measurements are highly informative, especially J coupling constants. Both chemical shifts and J couplings can be computed and could be used in matching experimental data. Several types of NMR experiments can be used to measure homo- and heteronuclear scalar coupling constants through one or more bonds,⁴⁸⁸ and if the data could be effectively used, then it could be more routinely measured in a metabolomics workflow. Currently, unknown identification of molecules perhaps relies too much on the chemical shift alone. This is especially problematic given that ¹H chemical shifts can be dependent on several variables including solvent, pH, ions, and temperature. Other nuclei, including ¹³C,⁴⁸⁹ are less dependent on these variables. A combination of computed ¹H and ¹³C chemical shifts, along with J coupling values, would be very valuable for increasing our confidence in unknown metabolite identification. This type of information is now available through QM calculations coupled to spin dynamics simulations.^490,491

While it would be useful to have a large database of results from high-level QM calculations of metabolites and other small molecules, that is still impossible because of the time required for each calculation, especially for flexible molecules that require conformational averaging. Prioritizing which compounds to calculate is a challenging question. The Brüschweiler lab has developed an interesting approach called Structure of Unknown Metabolomic Mixture components by MS/NMR (SUMMIT) that combines high-resolution MS and NMR data with computation.⁴⁹² In SUMMIT, high-resolution MS data are used to determine the molecular formula of an unknown peak of interest. Next, a database of known structures such as Chemspider⁴⁹³ is used to generate all possible molecules consistent with the experimental molecular formula. Then, NMR chemical shifts are computed for each potential molecule, and computational results are compared with experimental NMR data of the same sample. The primary difficulty with the SUMMIT approach is the large number of possible molecules as the molecular weight increases. There are at least two approaches to deal with this problem. First, one could use lower-level theory that could be effectively applied to hundreds or thousands of candidates. However, as the level of theory decreases, so does the accuracy of the calculation, so matching the correct one against experimental data would be difficult. Another idea is to add an additional layer of filtering, such as additional chemical data such as CCS or biological/genetic knowledge of pathways. if genomic data can be incorporated and related to the unknown feature of interest.

QM simulations of spectroscopic data of organic compounds is ripe to be used for compound identification within metabolomics. Of course, this application will only be really accomplished if a standardized protocol is adopted and an open-access computational database is established. Furthermore, experimental advances are required to make cryogenic gas-phase spectroscopy commercially available, which would offer an ideal pairing with QM calculations. Foreseeing the future advancement of quantum computers, one can easily expect a huge development in high-level spectroscopic simulations. Computing time will be reduced in orders of magnitude and an increasing number of variables (such as solvent, temperature, pH, matrix effects, etc.) could be implemented within the calculations. Thus, to have a seed already in place for a community-driven effort to catalogue simulated data in a common database will be a shortcut for the success of many other life-sciences-based studies.

4.2. Comparison to Machine and Deep Learning

Recent advances in deep learning^494−496 have shown promise in predicting physiochemical properties previously reliant on quantum chemical calculations, such as CCS, NMR chemical shifts, and MS fragmentation patterns,^{209,497−500} as well as replacing quantum chemical calculations entirely.^501−504 Deep learning has demonstrated improvements in property prediction accuracy compared to quantum-chemistry-based approaches, while reducing per-structure computation time by orders of magnitude (hours for quantum chemical, versus milliseconds with deep learning after training).^497,505 Similar improvements are seen with deep-learning-based DFT: orders of magnitude reduction in computation time with sub-1% MAE.⁵⁰² For generative approaches, including autoencoder and adversarial networks,^505−516 deep learning offers additional potential in addressing the inverse quantitative structure–property relationship (QSPR) problem,^517−519 wherein molecular structure candidates can be determined from physiochemical property/properties. However, with deep learning follows considerations to training time, which better contextualizes per-structure computation time, and generalizability, or to what extent does prediction accuracy degrade as inputs vary from the training set.

4.2.2. Generalizability

The greatest concern when evaluating deep learning models against first-principles approaches is generalizability, the model’s ability to operate successfully outside of the data set on which it was trained. With first-principles approaches, calculations are based on the underlying physics of the quantum-chemical system and are thus less biased to the structures seen, or not seen, during training. As such, a completely novel structure, when simulated by a first-principles approach, is beholden to low-level physical constraints/laws. A spurious prediction is unlikely, as the underlying physics remains constant across chemical space, both known and, presumably, unknown. With a poorly generalized deep learning model, an evaluated structure that exists outside the space defined by the training set may not have a robust basis for prediction, for example, either returning the average of the training set or a near-random result.

Therefore, it is important to sufficiently cover chemical space such that the probability of an out-of-sample compound significantly differs from the networks internal representation of structure/property is minimized. Given estimates of up to 10⁶⁰ potential unique structures, and that the union of all public databases amounts to only a few billion unique structures, complete chemical space coverage with current chemical knowledge cannot be guaranteed.^520−523 However, a wide range of properties, both empirical and qualitative, can be sampled to ensure coverage of descriptors used to define a chemical subspace. In deep learning applications in property prediction,^506−516 data are curated to represent a wide sampling of chemical space, relevant to the domain of application, and additional measures (cross validation, checkpointing, early stopping, learning rate decay) are taken to minimize overfitting, together maximizing model generality. As a result, the validation error, the error among predictions withheld for evaluation purposes, is only slightly higher than among predictions from data the model was trained on. This is promising as an initial assessment of the generality of such models, but as chemical space is further expanded and characterized, models should be continuously evaluated.

4.2.3. Computation Time

While per-structure computation time improves substantially when comparing deep learning to quantum chemical calculations, it is important to contextualize with required training times, which vary based on complexity of the considered network and the number of training examples. Other considerations, such as cascade or transfer learning configurations, additionally contribute to an increase in total train time. For example, a network with 5.6 million trainable parameters, trained on over 50 million chemical structures gleaned from several public databases, including PubChem,⁵²⁴ UNPD,⁵²⁵ HMDB,⁵²⁶ and DSSTox,⁵²⁷ and a curated data set with ∼500 experimental CCS values (metabolomics.pnnl.gov), requires approximately 123 h of training on a single Nvidia Tesla V100 GPU.

This compares first-principles approaches for CCS prediction,^497,499,500 which require on the order of hours per structure on a dual-socket Intel Haswell E5-2670v3 CPU. For example, employing the B3LYP exchange-correlation functional^528−531 and 6-31+G** basis set^532,533 for DFT optimization alone requires, on average, approximately 1 node-hour per conformation sampled. Propertion prediction methods involve 10 s to 100 s of conformations, rapidly increasing the per-molecule computation time. Of course, relaxing the level of DFT theory reduces computation time, although at a penalty to accuracy. This speedup extends to other physiochemical properties in which deep learning has been applied, i.e., for NMR chemical shifts^{210,243,534,535} and MS fragmentation patterns.⁵³⁶ IR spectral prediction has yet to see a deep learning solution, but we would expect computation time to follow similar trends.

Thus, although training via machine learning requires substantial computational resources up front, we remember that, once trained, each structure can be processed on the order of milliseconds, motivating deep learning use when computational efficiency is of chief importance, e.g., when building massive in silico libraries.

4.2.4. Accuracy

Among evaluated in silico prediction pipelines for CCS prediction, the best performing method resulted in an average unsigned error of 3.2%, with other methods achieving around 5% error when evaluated on the same structures. This error was achieved using the B3LYP exchange-correlation functional and 6-31+G** basis set. Higher levels of theory have been shown to reduce this error by up to 70%, but at a 2 orders of magnitude increase in computation time.⁴⁹⁷ In contrast, deep learning has been employed to reach an average error of 2.4%, or a 25% reduction compared to first-principles approaches. Similarly, generative deep learning approaches for use in inverse QSPR applications, although sacrificing in property prediction accuracy, still improve over first-principles simulation with an average error of 3.0%.⁵⁰⁵

In applications involving NMR chemical shifts, deep,⁵³⁴ and machine²⁴³ learning approaches were able to achieve MAE of 0.37 and 0.28 ppm for ¹H shifts, respectively, and 3.3 and 3.9 ppm for ¹³C shifts, respectively. These methods have not yet reached the accuracy provided by quantum chemical calculations, wherein MAE for ¹H and ¹³C predictions can be <0.1 and <1 ppm, respectively.²⁰⁴

With respect to mass fragmentation pattern prediction, most machine learning solutions have been developed for peptide fragment prediction and produce high accuracy results (up to 0.99 Pearson correlation coefficient with experimental spectra).^537−541 Of course, fragmentation pattern prediction of metabolites represents additional challenges, and these results are thus not directly comparable. Unfortunately, the number of deep or machine learning approaches to metabolite fragmentation pattern prediction is limited. Brouard et al. implemented an input/output kernel regression technique and compared to a commonly used fragment prediction tool: CSI:FingerID.⁵³⁶ Results indicated minor improvements over existing techniques, representing a 1–2% increase in top-k accuracy (37.8, 69.7, and 78.4% versus 36.0, 67.5, 76.5% for top 1, 5, and 10 accuracy, respectively, in positive ionization mode).

4.2.5. Inverse QSPR

An advantage to deep learning approaches, specifically those involving generative models, is their usefulness in inverse QSPR applications. The inverse QSPR problem involves determining a putative structure (or structures) based on chemical properties, for example, determining the structures that correspond to a given experimental m/z and some combination of CCS, NMR chemical shifts, IR spectra, and/or mass fragmentation pattern. With a variational autoencoder, for example, the network learns a continuous numerical, or latent, representation of the modeled structure.⁵⁴² Those dimensions of the latent representation determined to be uncorrelated with the properties of interest can be traversed to yield putative structures. Thus, the uncorrelated dimensions are varied, yet those correlated with the properties of interest remain largely invariant.

Under this framework, experimental features can be used to identify matching in-sample structures within a tolerance. These seed structures can then be perturbed as discussed to yield new structures with matching experimental signatures. This method does not solve the inverse QSPR problem because there is no guarantee the “true” structure will be generated. However, this method offers the ability to generate putative structures previously limited to those found in databases for use in high throughput virtual screening and similar approaches.

4.2.6. Interplay

Importantly, first-principles simulations and deep learning models can be leveraged for mutual benefit. Often, experimentally derived chemical properties of prediction interest are limited; for example, the union of all publicly available experimental CCS values contains only a few thousand unique structures. Training on such a limited data set, particularly when employing a large neural network, results in susceptibility to overfitting effects and, by extension, negatively affects generality. Instead, first-principles approaches can be used to expand the number of training labels, albeit with associated error, to gain broader chemical space coverage. Training can then be performed on the in silico values initially, followed by a round of experimental “fine tuning” to correct for the inherent error modeled from the in silico data. This allows for training on significantly larger data sets than would be possible with experimental values alone, the model thus learning from a broader sampling of chemical space.

Equally useful is the use of deep learning in an in silico property prediction pipeline, particularly used to replace computationally expensive quantum chemical calculations, e.g., DFT. Under this paradigm, quantum chemical simulations are used to solve electronic structures of molecules for use in a training set. Deep learning is then leveraged to predict electronic structures from representations of atom types, positions, and chemical environments amenable to consumption by a neural network. Although data sets have thus far been fairly limited, in both size and complexity, initial results show promise with MAE less than 1%.⁵⁰²

In addition, a cascade of techniques can be combined for virtual high-throughput screening, i.e., initially down-select chemical space based on machine-learning-predicted properties, verify putative structures and associated properties with quantum mechanical simulations, and confirm by experimentation. This paradigm represents a path from low cost, high throughput to high cost, low throughput, enabling researchers to efficiently use both computational and experimental resources.

Glossary

Abbreviations

AIMD

ab initio molecular dynamics

AWS

Amazon Web Services

BOMD

Born–Oppenheimer molecular dynamics

CAD

collision-activation decomposition

CASE

computer aided structure elucidation

CCS

collision cross section

CD

circular dichroism

CE

capillary electrophoresis

CID

collision-induced dissociation

CIS

configuration interaction singles

DFT

density functional theory

EI

electron ionization

ESI

electrospray ionization

FDA

U.S. Food and Drug Administration

FF

force field

FTICR

Fourier transform ion cyclotron resonance

GC

gas chromatography

GRRM

global reaction route mapping

HMDB

Human Metabolome Database

HPC

high-performance computing

IEE

internal excess energies

IMS

ion mobility spectrometry

IP

ionization potential

IR

infrared

IRIS

infrared ion spectroscopy

IRMPD

infrared multiple-photon dissociation spectroscopy

ISiCLE

In Silico Chemical Library Engine

KS-DFT

Kohn–Sham density functional theory

LC

liquid chromatography

LSD

logic for structure determination

MAE

mean absolute error

MC

Monte Carlo

MD

molecular dynamics

ML

machine learning

MO

molecular orbital

MS

MS

MS/MS

tandem MS

MSI

Metabolomics Standards Initiative

NMR

nuclear magnetic resonance

PEPICO

photoelectron photoion coincidence

PES

potential energy surface

PKU

phenylketonuria

QCEIMS

quantum chemistry electron ionization MS

QET

quasi-equilibrium theory

QM

quantum mechanical

QQQ

triple-quadrupole

QSPR

quantitative structure–property relationship

Q-TOF

quadrupole-time-of-flight

RRKM

Rice–Ramsperger–Kassel–Marcus

SUMMIT

structure of unknown metabolomic mixture components by MS/NMR

TD-DFT

time-dependent density functional theory

TMS

trimethylsilyl

TOF

time of flight

Biographies

Ricardo M. Borges completed his B.S. degree in pharmacy from the Federal University of Rio de Janeiro (UFRJ, Brazil) in 2004 and M.S. and Ph.D. degrees from the Walter Mors Institute of Research on Natural Products (IPPN) at the same university in 2006 and 2010. During this period, he was focusing his research on the isolation and structure elucidation methods such as in classic natural products research. Today, as PI in the same IPPN-UFRJ since 2012, his main effort is on the development of approaches for compound identification in mixtures with natural products metabolomics combining the use of MS and NMR.

Sean M. Colby is a Data Scientist in the Earth and Biological Sciences Division at Pacific Northwest National Laboratory. He received a master’s degree in computer science from the Georgia Institute of Technology. His research involves in silico predictions of physiochemical properties by both quantum mechanical simulation and machine learning, as well as the cheminformatics pipeline metabolomic analysis relies upon. His effort has led to the development of ISiCLE, the in silico chemical library engine, DarkChem, a deep learning framework for molecular property prediction, and DEIMoS, data extraction in integrated multidimension spectrometry.

Susanta Das received a Ph.D. in 2015 from CSIR-National Chemical Laboratory, India (with Dr. Sourav Pal). He joined Bar-Ilan University, Israel in 2015 for postdoctoral work with Dr. Dan T. Major, where he focused on development of QM/MM simulation strategies, protein–ligand docking protocol (viz. EnzyDock), and enzyme catalysis applying QM/MM methods. He moved to USA in 2019 and start working with Dr. Kenneth M. Merz Jr. at Michigan State University as a postdoctoral researcher. His research with Merz group focused on in silico NMR and MS-based protocol development for structure identification of metabolites using FF, ML, and high-level quantum mechanical (QM) method.

Arthur S. Edison is a Georgia Research Alliance Eminent Scholar and Professor of Genetics and Biochemistry and a member of the Complex Carbohydrate Research Center and Institute of Bioinformatics at the University of Georgia. He received his Ph.D. in biophysics from the University of Wisconsin–Madison under joint supervision of John Markley and Frank Weinhold. He joined the faculty at the University of Florida and the National High Magnetic Field Laboratory in 1996. He was the founding PI and Director of the NIH-funded Southeast Center for Integrated Metabolomics. In 2015, Prof. Edison moved to the University of Georgia, where he directs the CCRC NMR facility, which supports research in both metabolomics and structural biology. Edison’s research group collaborates on several metabolomics projects from microbes to humans.

Oliver Fiehn has pioneered developments and applications in metabolomics with over 320 publications to date, starting in 2000 as group leader at the Max-Planck Institute in Potsdam, Germany. Since 2004, he has been a professor at the University of California, Davis. Since 2012, he has served as Director of the NIH West Coast Metabolomics Center, overseeing his research laboratory and the satellite core service with 35 staff and 17 mass spectrometers. Professor Fiehn’s research laboratory develops and implements new analytical technologies and databases for covering the metabolome. He studies fundamental biochemical questions from metabolite damage repair to epimetabolites in human diseases and animal models.

Tobias Kind is an Associate Project Scientist at the West Coast Metabolomics Center and UC Davis Genome Center. His research projects focus on the advancement of structure elucidation techniques and databases for small molecule identifications. His research interests include computational metabolomics and MS, cheminformatics, machine learning, and deep learning as well as quantum chemistry for the creation of in silico spectra.

Jesi Lee is a Ph.D. student under the supervision of Dr. Lee-Ping Wang and Dr. Oliver Fiehn in the Chemistry Department at the University of California, Davis. She is interested in using ab initio and semiempirical molecular dynamics to simulate collision-induced dissociation for improving in silico MS libraries.

Amy T. Merrill obtained her B.S. in chemistry at California Polytechnic State University San Luis Obispo in 2015, where she researched alkoxyamine and oxime ether synthesis with Professor Hasan Palandoken. She is currently a Ph.D. candidate with Professor Dean J. Tantillo. Her dissertation research focuses on structure elucidation of natural products and method development in computational NMR.

Kenneth M. Merz, Jr., is the Joseph Zichis Chair in Chemistry at Michigan State University and is the Editor-in-Chief of the Journal of Chemical Information and Modeling. His research interests lie in the development of theoretical and computational tools and their application to chemical and biological problems including structure and ligand-based drug design, mechanistic enzymology, transition ion modeling, and methodological verification and validation. He has received numerous honors, including election as an ACS Fellow, the 2010 ACS Award for Computers in Chemical and Pharmaceutical Research, election as a fellow of the American Association for the Advancement of Science, and a John Simon Guggenheim Fellowship. When not doing science, he enjoys (re)reading the novels of Jane Austen.

Thomas O. Metz joined Pacific Northwest National Laboratory in 2003 for postdoctoral work in MS with Dr. Richard D. Smith, where he focused on metabolomics. He became Staff Scientist and a Principal Investigator in the Integrative Omics Group in 2005 and is the Metabolomics Team Lead for a group of scientists that focuses on development and applications of high-throughput metabolomics and lipidomics methods to various biological questions. Dr. Metz’s research has focused primarily on applying MS-based omics approaches, including proteomics, in studies of diabetes mellitus and infectious diseases, resulting in over 150 publications to date. Currently, he is the Director of the Pacific Northwest Advanced Compound Identification Core within the NIH Common Fund Metabolomics Program.

Jamie R. Nunez is working as a Data Scientist at PNNL while also pursuing a Ph.D. under the supervision of Ryan Renslow in the Chemical Engineering department at Washington State University. Her work encompasses the full metabolomics pipeline (from experimental methods to interpretation of final results) but has primarily focused on scoring for the reporting of identification results using the Multi-Attribute Matching Engine (MAME) and methods to improve confidence.

Dean J. Tantillo was born and raised in Quincy, Massachusetts, USA. He received an A.B. degree in chemistry in 1995 from Harvard and a Ph.D. in 2000 from UCLA (with Ken Houk) and then moved to Cornell, where he did postdoctoral research with Roald Hoffmann. Dean joined the faculty at UC Davis in 2003. Research in Dean’s group is driven by puzzling mechanistic questions in the areas of biosynthesis, organometallic chemistry, and stereoselective synthetic reactions, with a focus on cyclization/rearrangement reactions used by Nature and by chemists to synthesize complex natural products.

Lee-Ping Wang was born and raised in the East Bay region of California and studied physics at UC Berkeley (B.A. 2006). He attended graduate school in physical chemistry at MIT advised by Troy Van Voorhis (Ph.D. 2001) and did research as a postdoc at Stanford with Todd Martinez and Vijay Pande. He joined the UC Davis Chemistry Department in 2015 and was promoted to associate professor as of July 2020. Lee-Ping’s core research interests are at the intersection of quantum chemistry and molecular dynamics, where he develops methods for reaction pathway discovery and force field optimization and applies them to diverse problems in collaboration with experiment, including metabolomics.

Shunyang Wang is a doctoral student at University of California, Davis. He obtained a B.S. degree in chemistry from the Shandong University in 2018, and his doctoral work is focused on predicting mass spectra.

Ryan S. Renslow leads a team of researchers focused on computational methods to accelerate small-molecule identification in complex samples in the Biological Science Division at the Pacific Northwest National Laboratory (PNNL). He is also an associate research professor in The Gene and Linda Voiland School of Chemical Engineering and Bioengineering at Washington State University. He received his Ph.D. in chemical engineering from Washington State University in 2012, after which he joined PNNL as a Linus Pauling Distinguished Postdoctoral Fellow (2012–2015). Currently he is the colead of the Computational Core of the Pacific Northwest Advanced Compound Identification Core. His current research centers on computational quantum chemistry, machine learning and artificial intelligence, and cheminformatics methods in metabolomics, exposomics, and chemical forensics applications.

The authors declare no competing financial interest.