Extended Data Fig. 6: An artificial alphabet optimized to maximize neural decodability.

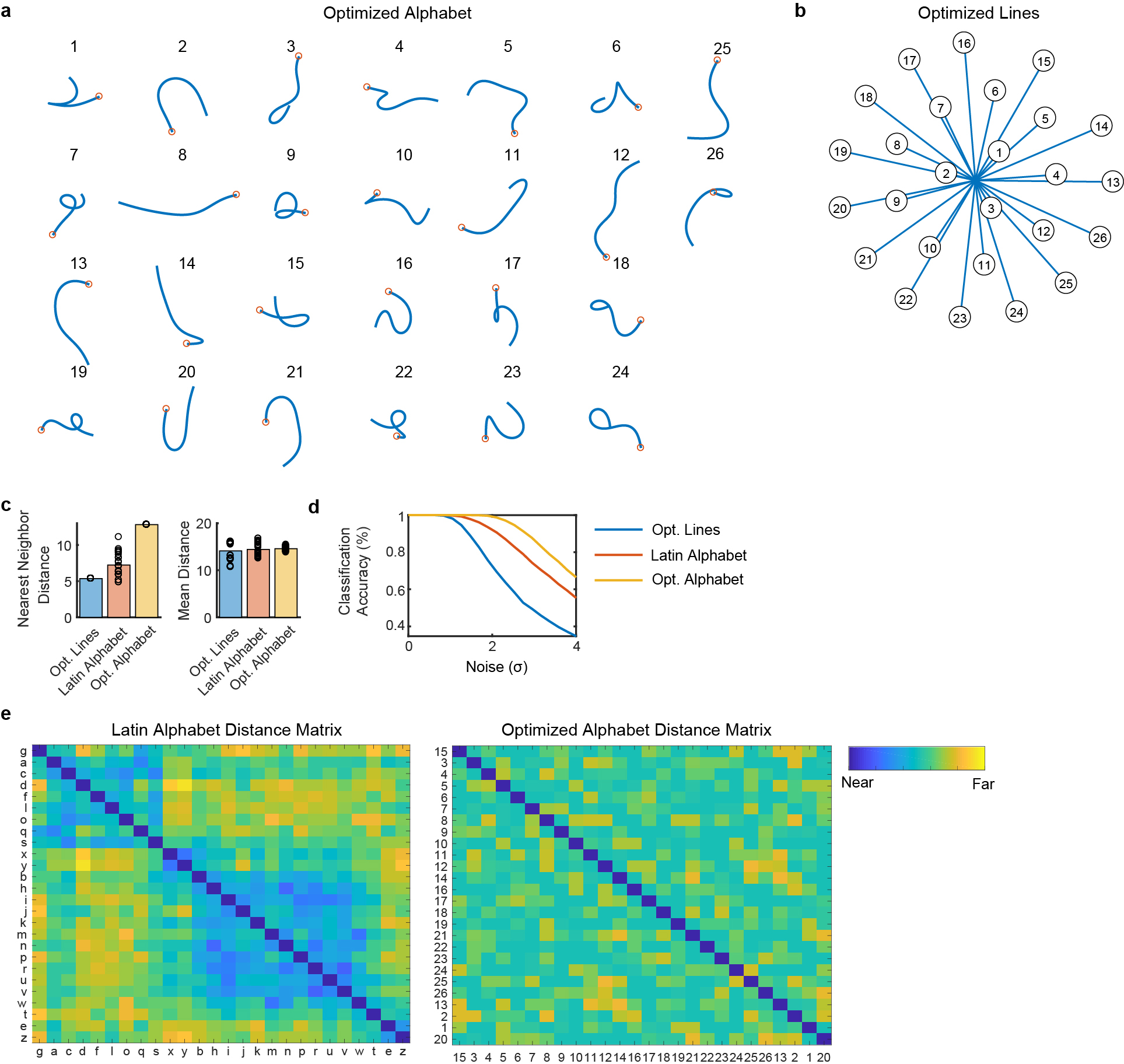
(A) Using the principle of maximizing the nearest neighbor distance, we optimized for a set of pen trajectories that are theoretically easier to classify than the Latin alphabet (using standard assumptions of linear neural tuning to pen tip velocity). (B) For comparison, we also optimized a set of 26 straight lines that maximize the nearest neighbor distance. (C) Pairwise Euclidean distances between pen tip trajectories were computed for each set, revealing a larger nearest neighbor distance (but not mean distance) for the optimized alphabet as compared to the Latin alphabet. Each circle represents a single movement and bar heights show the mean. (D) Simulated classification accuracy as a function of the amount of artificial noise added. Results confirm that the optimized alphabet is indeed easier to classify than the Latin alphabet, and that the Latin alphabet is much easier to classify than straight lines, even when the lines have been optimized. (E) Distance matrices for the Latin alphabet and optimized alphabets show the pairwise Euclidean distances between the pen trajectories. The distance matrices were sorted into 7 clusters using single-linkage hierarchical clustering. The distance matrix for the optimized alphabet has no apparent structure; in contrast, the Latin alphabet has two large clusters of similar letters (letters that begin with a counter-clockwise curl, and letters that begin with a down stroke).