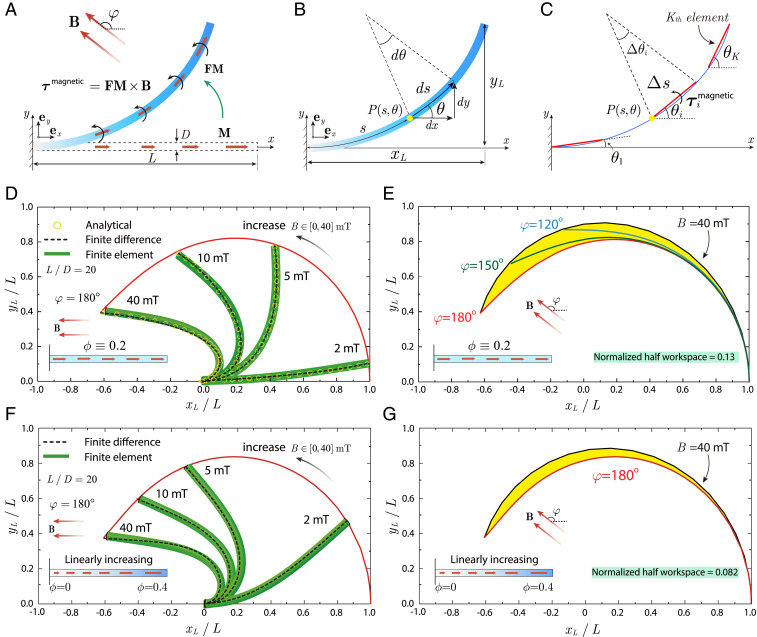
Fig. 3.

Theoretical modeling of the distal portion of an MSCR. (A) Schematic illustration of the distal portion of a MSCR with remanent magnetization $\text{M}$ along its axial direction deflecting toward the direction of the uniform actuation magnetic field B. The length and diameter of the distal portion are denoted as $L$ and $D$, respectively. (B) The deformed distal portion is characterized by a parameterized spatial curve $\theta \hspace{0.17em}=\hspace{0.17em}\theta \left(s\right)$, referred to as an elastica, where $s$ and $\theta$ represent the arc length and tangential angle at the spatial point $P\left(s,\theta \right)$, respectively. The Cartesian coordinates of the distal tip are $\left(x_L,y_L\right)$. (C) The finite difference method discretizes the elastica into $K$ elements in which the infinitesimal arc $ds$ is approximated by a straight line $\mathrm{\Delta }s=L/K$. (D) Comparison of the deformation of the distal portion with uniform magnetic particle distribution $\varphi =0.2$ under 180° magnetic field from the analytical solution, finite difference method, and finite element simulation. (E) The normalized half workspace of the MSCR with uniform magnetic particle distribution $\varphi =0.2$ is 0.13. (F) Comparison of the deformation of the distal portion with linearly increasing particle concentration from 0 to 0.4 under 180° magnetic field from the finite difference method and finite element simulation. (G) The normalized half workspace of the MSCR with linearly increasing magnetic particle concentration from 0 to 0.4 is 0.082.