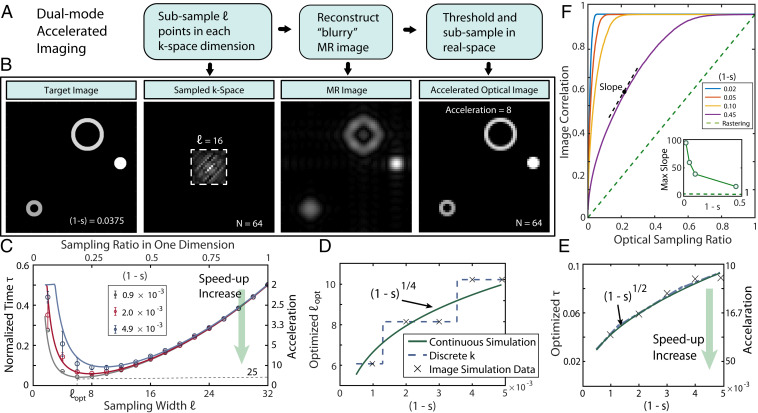
Fig. 4.

Accelerated x-k conjugate-space imaging. (A) Protocol for accelerated imaging. $\ell$ samples of the image are first acquired in k-space, and the resulting image upon thresholding is fed forward to constrain the real-space points to be scanned over. (B) Exemplary scenario where the target image FOV consists of sparsely distributed objects. By sampling over $\ell$ = 16 k-space points in each dimension, a blurry yet faithful image is formed of the target (Center two panels) and can serve to restrict real-space sampling (Right panel), leading to $\sim$14 times acceleration. (C) Normalized imaging time $\tau$ with different values of $\ell$ for images in a ${\mathrm{32}}^2$-pixel square FOV of different sparsity factors. Right axis indicates corresponding imaging acceleration. Here images consisted of unit-pixel objects, and we averaged over 30 random image configurations with identical sparsity; error bars denote standard deviations. The presence of an optimal k-space sample threshold ${\ell }_{\mathrm{\text{opt}}}$ is evident, stemming from a compromise between better confinement in real-space imaging and associated time cost for k-space imaging. (D) Scaling of ${\ell }_{\mathrm{\text{opt}}}$ with image sparsity, showing that more k-space values are required to account for increasing imaging complexity. Points: Given discrete possible values of $k$, ${\ell }_{\mathrm{\text{opt}}}$ has a staircase-like behavior. Solid line: scaling of ${\ell }_{\mathrm{\text{opt}}}$ assuming continuous $k$ values. (E) Optimized imaging acceleration through sampling ${\ell }_{\mathrm{\text{opt}}}$ points, showing orders of magnitude time savings at high sparsity. (F) Trajectory of image convergence quantified by image correlation $\mathcal{C}$ with protocol advancement. Green dashed line shows linear convergence under conventional optical rastering. In contrast, hybrid sampling in conjugate spaces can lead to rapid image convergence. (Inset) Slope of image approach to target rapidly increases with sparsity.