Figure 5. Model of the abscisic acid–gibberellic acid (ABA-GA) bistable switch and effect of ABA sensitivity parameter on germination traits.
(A) Model scheme of the ABA-GA network. Normal arrows represent effective promotion and blunt arrows represent effective inhibition. We represent the inhibitors of germination – DELLAs, ABI4 and ABI5 – as one factor, called Integrator, which we assume must drop below a threshold for germination to occur. We assume that ABA promotes the production of Integrator and that GA promotes its degradation. Integrator is assumed to promote ABA production and inhibit GA production. A factor, Z, increases upon sowing and promotes GA production. Figure 5—figure supplement 1 provides information on the dynamics of the model. (B) Effects on coefficient of variation (CV), mode and percentage germination of simulated germination time distributions as the ABA threshold for Integrator (I) production parameter values are changed. This parameter is inversely correlated with sensitivity of Integrator to ABA. Each panel shows the results of three different runs of stochastic simulations on 4000 seeds. (C) Simulated germination time distributions for six values of the ABA threshold for Integrator production parameter, showing positively correlated changes in CV and mode. The arrow indicates increasing sensitivity of Integrator production to ABA towards the top left. (D) CV, mode and percentage germination in bistable and monostable regions of the model parameter space after the rise in GA production (see Figure 5—figure supplement 1 for details of monostable and bistable regimes). See Materials and methods for regions of the parameter space that we exclude from these plots because they are considered less biologically relevant. Colours in (B) and (D) represent different runs of stochastic simulations. See Materials and methods for further details on parameters and numerical simulations.
Figure 5—figure supplement 1. Dynamics of the components of the abscisic acid–gibberellic acid (ABA-GA) model in monostable and bistable regimes.
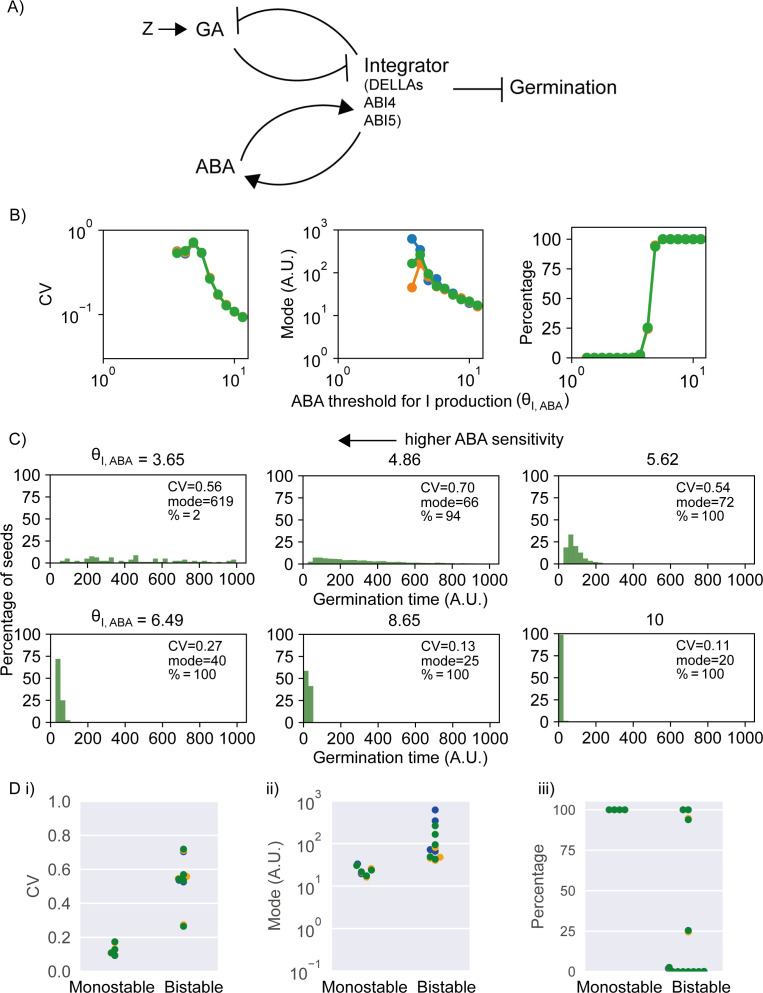
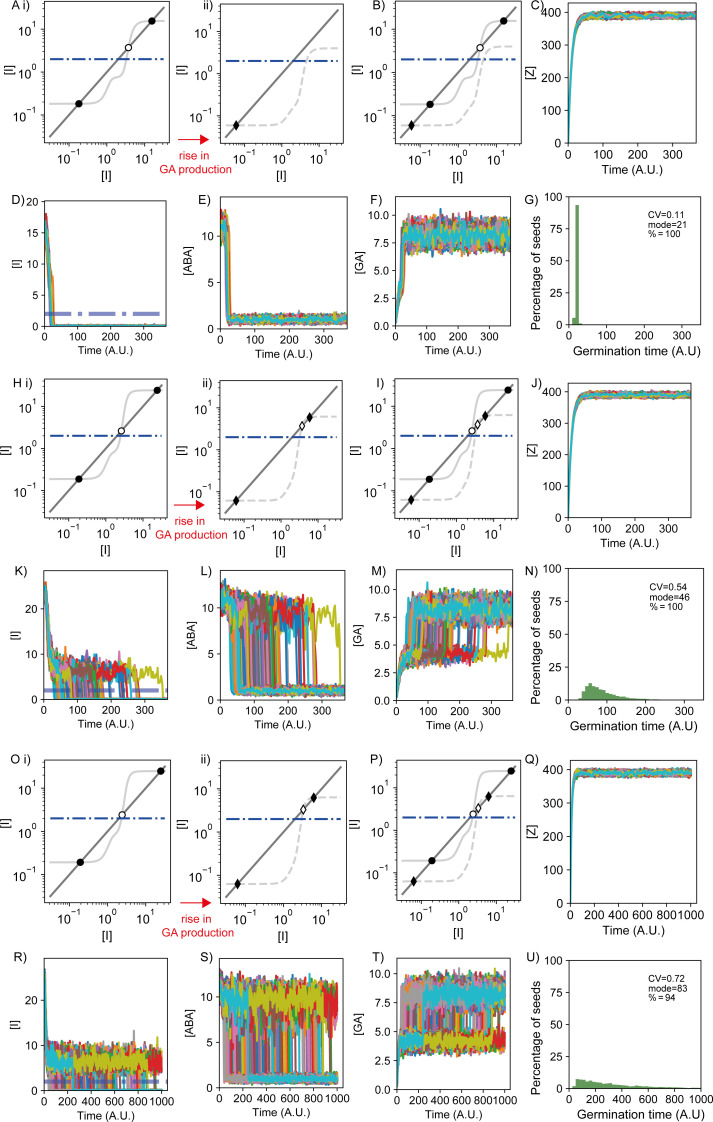
Modelling results showing representative behaviour of the model when it is in the monostable (A–G) and two bistable scenarios (H–U) after the rise of GA production (referred to as monostable and bistable scenarios for simplicity). (H–N) show a bistable scenario where the non-germination steady state is less stable than the second bistable scenario shown in (O–U). The three scenarios differ in the ABA threshold for integrator production, which modulates ABA sensitivity: the monostable scenario in (A–G) has the highest value of this parameter (θI,ABA = 10), and therefore lowest ABA sensitivity, the first bistable scenario in (H–N) has an intermediate ABA sensitivity (θI,ABA = 5.6) and the second bistable scenario in (O–U) has the highest ABA sensitivity (θI,ABA = 4.87). 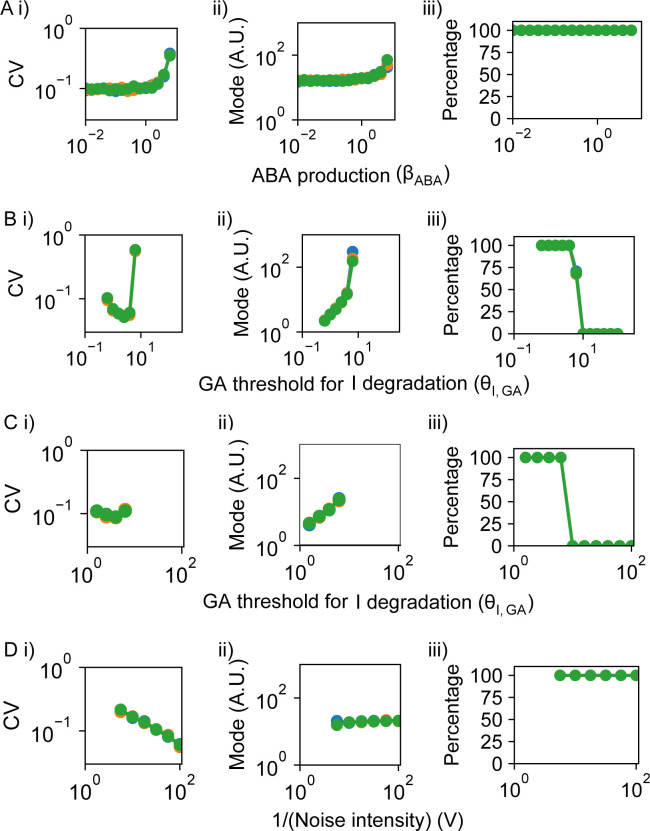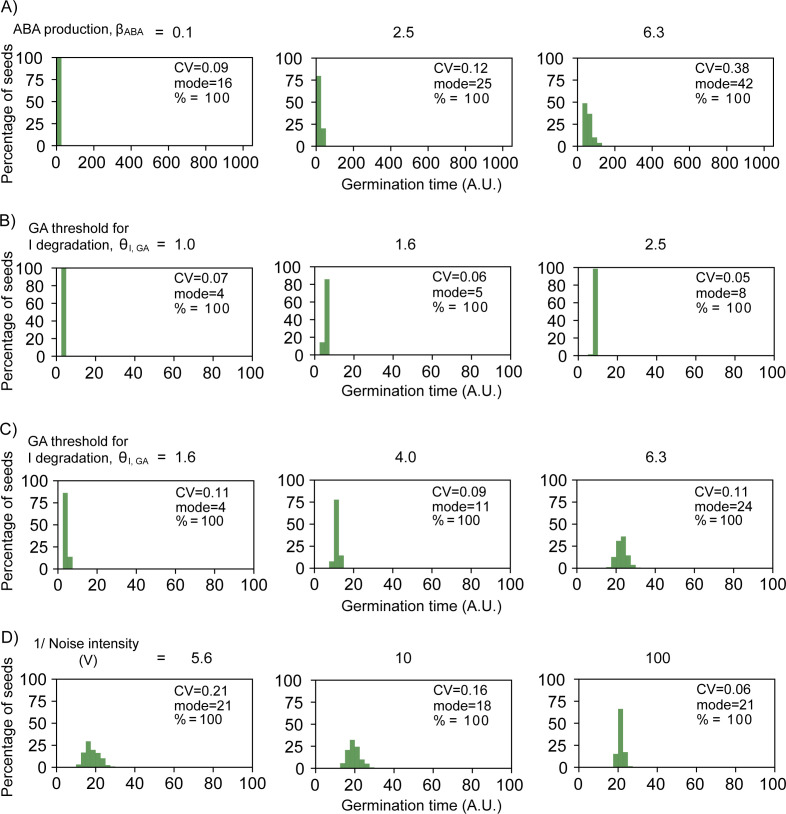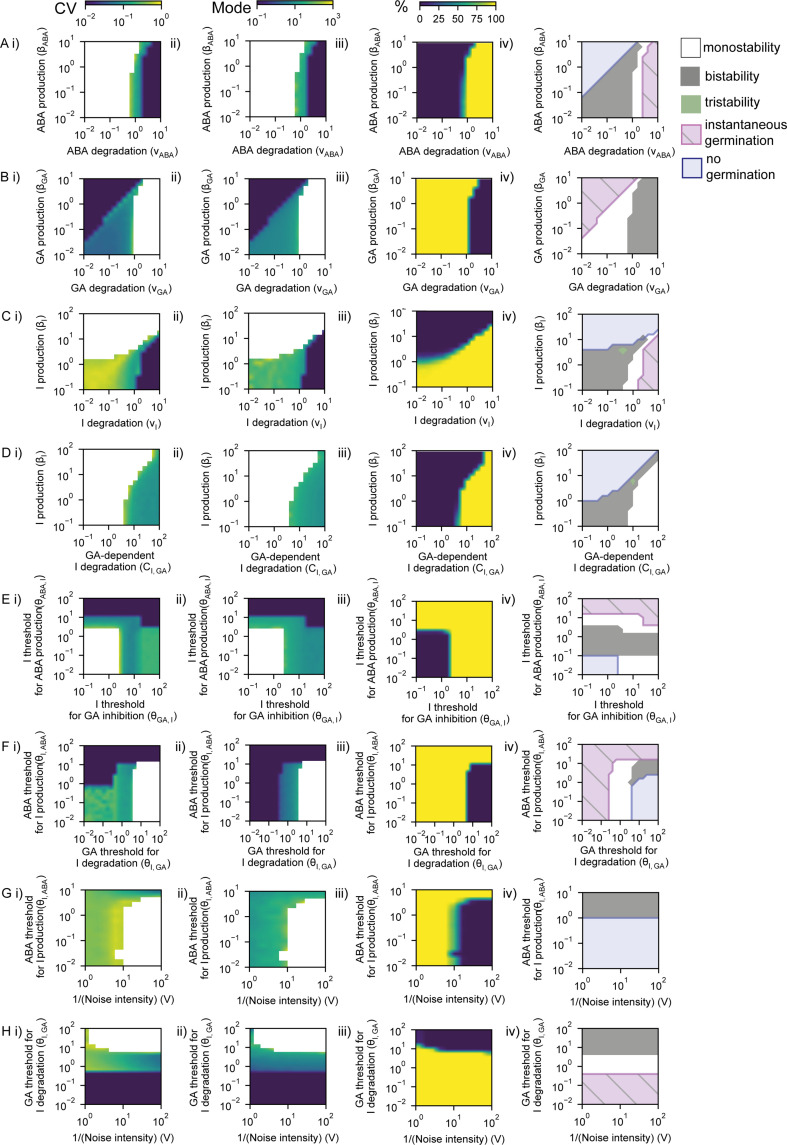The bistable scenarios correspond to the grey region in the phase diagrams shown in Figure 5—figure supplement 4, and the monostable scenario corresponds to the white regions. (A, H, O) Results from nullcline analysis for the Integrator variable showing the steady states of the dynamics before (i) and after (ii) the GA production increase (see Materials and methods). In each panel, steady-state solutions are shown by the intersections between the dark grey line and the light grey line. Filled dots and diamonds represent the Integrator stable steady states before and after the GA production increase, respectively. Empty dots and diamonds represent unstable steady states. The dashed-dotted blue line illustrates the Integrator threshold below which germination happens. Before the increase of GA production, the modelled network exhibits a high Integrator stable steady state above the threshold (higher filled dot), representing a non-germinating state before sowing. We set this state as the initial condition of the simulation. For these parameter values, a lower Integrator stable solution below the germination threshold exists (lower filled dot), therefore representing a germination state, as well as an intermediate unstable Integrator solution (empty dot). Hence, bistability occurs for the Integrator variable before the increase of GA production. With the provided noise intensity for these simulations, none of the seeds is able to switch from the non-germination state to the germination state before the rise of GA production in the three scenarios (A), (H) and (O) (see Materials and methods). (Aii) In the monostable scenario after the rise in GA production, the increase in GA production leads to the disappearance of the non-germination state and the unstable steady state through a saddle node bifurcation; this makes the germination state the only possible stable state. (Hii, Oii) In the bistable scenarios after the rise in GA production, the non-germination state (high Integrator, high ABA and low GA) approaches the unstable steady state (empty dot), becoming less stable. In these cases, stochastic fluctuations enable the simulated seeds to cross the unstable steady state, reaching the germination state (low Integrator, low ABA and high GA), which becomes a more stable solution. (B, I, P) Nullclines analyses shown in (A), (H) and (O) subpanels, with the scenarios before and after the rise in GA production represented together. For each panel, the light grey solid line and dots show the case before the rise in GA production, and the light grey dashed line and diamonds show the case after the rise in GA production. (C–F, J–M, Q–T) Time courses for the components of the model in example simulations. Different coloured lines represent different seeds. (C, J, Q) Time courses of the concentration of the factor Z, which increases rapidly upon sowing and promotes GA production. (D, K, R) Time courses of Integrator concentrations. Dashed-dotted blue lines show the threshold below which Integrator must drop for germination to occur. (E, L, S) Time courses of ABA concentrations. (F, M, T) Time courses of GA concentrations. (G, N, U) Histograms of germination times, with values for coefficient of variation, mode and percentage germination of the distribution. Note that the x-axis range for the time courses and histograms is larger for (Q–U) due to the highly variable germination times in this scenario. The simulations representing the bistable scenarios show a transient in which the seeds can remain in a high Integrator state until the stochastic fluctuations cause them to switch to the low Integrator state. Conversely, in the monostable scenario, the seeds achieve the low Integrator state in a more direct manner. See Materials and methods for further details on parameters and numerical simulations.
Figure 5—figure supplement 2. Effect of model parameters on germination traits.
(A–D) show the effects on coefficient of variation (CV), mode and percentage germination of simulated germination time distributions as single parameter values are changed. Each panel shows the results of three different runs of stochastic simulations on 400 seeds, represented in different colours. (A) Varying the rate of abscisic acid (ABA) production as an example of a parameter that, when changed, tends to have positively correlated effects on CV and mode of germination time. (B) Varying the threshold of gibberellic acid (GA) for degradation of Integrator (this parameter is inversely correlated with sensitivity of Integrator to GA). For some points in parameter space, varying this parameter has anti-correlated effects on CV and mode. (C) As for (B), but in a different region in parameter space (see below for parameter details), in which increasing the threshold of GA for degradation of Integrator causes an increase in mode with relatively constant CV which indicates decoupled effects on CV and mode. (D) Varying the effective system volume parameter, V, which controls the level of noise in the system (we define noise intensity as being proportional to 1/V), also causing decoupled effects on CV and mode. For some areas of parameter space, an increase in V, and therefore a decrease in noise, causes the CV to decrease but leaves mode and percentage germination relatively unchanged. Parameter values are provided in the Materials and methods (Table 2) and were the same across simulations with the exception of the parameters varied on x-axes and differences in vABA in (A), V in (B) , θI,ABA in (C) and in (D). See Materials and methods for regions of the parameter space that we exclude from these plots because they are considered less biologically relevant. Figure 5—figure supplement 3 shows simulated germination time distributions corresponding to the parameter explorations in (A–D). Figure 5—figure supplement 4 shows the full results of the 2D parameter screen in terms of the effects of parameter pairs on CV, mode and percentage germination.
Figure 5—figure supplement 3. Simulated germination time distributions illustrating the effects of parameter value changes.
Histograms in (A), (B), (C) and (D) correspond to points in the plots in Figure 5—figure supplement 2 from (A), (B), (C) and (D), respectively. (A) Simulated germination time distributions for three values of abscisic acid (ABA) basal production, showing positively correlated changes in coefficient of variation (CV) and mode. (B) As for (A), but varying the gibberellic acid (GA) threshold for Integrator degradation (which is inversely proportional to Integrator sensitivity to GA), illustrating anti-correlated changes in mode and CV. (C) As for (B) but varying the GA threshold for Integrator degradation in an area of parameter space where the mode increases while the CV remains relatively constant. (D) As for (A) but varying the parameter V which governs the level of noise in the system, illustrating a change in CV while the mode remains relatively constant.
Figure 5—figure supplement 4. Exploring the effects of model parameters on coefficient of variation (CV), mode and percentage germination.
Each panel shows a result from a 2D parameter exploration for a pair of parameters, such that each parameter is varied for a range of values of a second parameter. (A) Effect of abscisic acid (ABA) basal production and ABA basal degradation parameters on CV (i), mode (ii) and percentage germination(%) (iii) of simulated germination distributions. CVs below 0.01 and above 1 are represented as being 0.01 and 1, respectively. CV and mode of the simulations were represented when there were more than nine seeds germinating out of 1000. (iv) Phase diagram showing theoretically predicted regions from nullcline analysis of the deterministic system: bistability (grey, see Figure 5—figure supplement 1B for information on this region) and tristability (green) regions in which we can expect the full range of behaviours in terms of germination percentage, region where we expect to have all seeds germinated instantaneously (pink hatched), and region where no seeds are expected to germinate in the deterministic limit (i.e. when there is no noise) (blue). The remaining white region is monostable, and we expect all seeds (non-instantaneously) to germinate (see Figure 5—figure supplement 1A, B for information on this region). We expect that just the bistable and tristable scenarios will allow a percentage of seeds to germinate that differs from 0% and 100%. The colour bars above (A) apply to all rows. All rows are as for (A), but exploring the following parameter pairs: (B) Gibberellic acid (GA) basal degradation versus GA basal production; (C) Integrator basal degradation versus Integrator basal production; (D) GA-dependent degradation of Integrator versus Integrator basal production; (E) threshold of Integrator for the inhibition of GA production (which is inversely correlated with sensitivity of GA to Integrator) versus threshold of Integrator for the promotion of ABA production (which is inversely correlated with sensitivity of ABA to Integrator); (F) threshold of GA for the GA-mediated degradation of Integrator (which is inversely correlated with sensitivity of Integrator to GA) versus threshold of ABA for the promotion of Integrator production (which is inversely correlated with sensitivity of Integrator to ABA); (G) effective volume of the system, V (which is inversely proportional to the noise in the system, see Materials and methods), versus threshold of ABA for the promotion of Integrator production; (H) effective volume of the system, V, versus threshold of GA for the degradation of Integrator. The theoretically predicted areas from nullclines (right panels) are closely predictive of the stochastic simulation outcomes (see Materials and methods). Figure 5—figure supplement 5 shows an analysis of the CV, mode of germination times and percentage germination in monostable and bistable regions of these parameter spaces. See Materials and methods for further details of the simulations and theoretical predictions and see Table 2 for full parameter values for each simulation.
Figure 5—figure supplement 5. Coefficient of variation (CV), mode of germination times and percentage germination in bistable and monostable regions of the model after the rise in GA production.
Simulation results across the different 2D parameter explorations shown in Figure 5—figure supplement 4A—G. In panels (A)-(G), points represent simulation results for different combinations of parameter values for the parameter pair indicated on the right. Panels show: i) CV, ii) mode and iii) percentage germination of simulated germination time distributions. Colours represent different runs of stochastic simulations. This analysis focuses on biologically relevant points falling within the monostable and bistable regions (see Materials and methods regarding the excluded, less biologically relevant points). We obtained a similar result in relation to simulations shown in Figure 5—figure supplement 4H but have ommited this here for simplicity.