Abstract
The prediction of the spread of coronavirus disease 2019 (COVID-19) is vital in taking preventive and control measures to reduce human health damage. The Grey Modelling (1,1) is a popular approach used to construct a predictive model with a small-sized dataset. In this study, a hybrid model based on grey prediction and rolling mechanism optimized by particle swarm optimization algorithm (PSO) was applied to create short-term estimates of the total number of confirmed COVID-19 cases for three countries, Germany, Turkey, and the USA. A rolling mechanism that updates data in equal dimensions was applied to improve the forecasting accuracy of the models. The PSO algorithm was used to optimize the Grey Modelling parameters (1,1) to provide more robust and efficient solutions with minimum errors. To compare the accuracy of the predictive models, a nonlinear autoregressive neural network (NARNN) was also developed. According to the analysis results, Grey Rolling Modelling (1,1) optimized by PSO algorithm performs better than the classical Grey Modelling (1,1), Grey Rolling Modelling (1,1), and NARNN models for predicting the total number of confirmed COVID-19 cases. The present study can provide an important basis for countries to allocate health resources and formulate epidemic prevention policies effectively.
Keywords: COVID-19; Prediction; NARNN; Grey modelling (1,1); Rolling mechanism; Particle swarm optimization
1. Introduction
Millions of people were infected and died due to the new coronavirus disease 2019 (COVID-19), which started at the end of 2019 and affected the whole world in a short time. As a first significant warning against the severe effects of the epidemic, a global pandemic was declared by the World Health Organization (WHO) on March 11, and the world was alarmed [1]. The spread rate, high aggressiveness, and severe damage ability of COVID-19 pose a significant threat to the health and safety of all humanity. While the epidemic has exceeded its peak in many countries, it continues to spread rapidly worldwide. Although the outbreak was brought under control in China, which was the starting point, Europe and America became the new epidemic centres [2].
COVID-19 has become a top priority for researchers worldwide [3], [4]. In general, epidemics have a cycle that resembles a bell curve. At first, the epidemic spreads quickly. After a while, it makes a plateau, and then the spread rate (number of infected people) begins to decrease. The time to reach the turning point is related to the dynamics of the countries, and it may differ. These phases of the outbreak are similar to the shape of a bell curve. The form of the bell-curve is related to the policies that countries apply against the epidemic. In countries that strictly follow the rules and have effective interventions, there will be a broader peak with a lower height. However, in countries that are late to react or implement wrong strategies, a sharp curve will emerge. Of course, this means more infected people, loss of life, and income.
Considering the size and impact of the outbreak, effective healthcare system management is essential to provide fast and accurate treatment for people with COVID-19 symptoms. Thus, it is very important to predict the intensity to be experienced and know the number of cases in advance to provide adequate and timely health care. For this purpose, various studies have been conducted in the literature using different mathematical models to predict the spread of the COVID-19 epidemic [5], [6], [7].
Grey prediction models have arisen as a rapid and straightforward modelling and forecasting tool in grey system theory. Grey Modelling (1,1), also abbreviated as GM (1,1), is the simplest primary time-series prediction model in grey system theory. It is the most commonly used grey prediction model in the literature because of its computational efficiency and ability to characterize an unknown system using a limited amount of data [8]. In recent years, the GM (1,1) model has shown satisfactory results in various fields such as environment [9], energy [10], manufacturing [11], transportation [12], and medicine and health [13].
As shown in Table 1, the classical GM (1,1) and its derived models have been used successfully in medicine to predict the spread of various infectious diseases. For example, Gao et al. (2007) used the GM (1,1) model for forecasting of malaria epidemic situation in Shenzhen Longgang areas [13]. Ding et al. (2011) compared the results of the GM (1,1) model and the D-R algorithm to estimate the trend of H1N1 cases in Mainland China [14]. Ren et al. (2012) analysed tuberculosis incidence rates and deaths in HIV-negative patients in the USA and Germany using the GM (1,1) model [15]. Shen et al. (2013) utilized the grey model to examine typhoid and paratyphoid fever epidemic peaks in China [16]. Guo et al. (2014) used the linear model, the traditional GM (1,1) model, and the GM (1,1) model with the self-memory principle (SMGM(1,1)) to forecast the incidence rates of two notifiable diseases in China [17]. Zhang et al. (2014) used various grey models to forecast the incidence of Hepatitis B in Xinjiang, China [18]. Zhang et al. (2017) applied the different grey models to predict human Echinococcosis spread in Xinjiang, China. They reported that the dynamic epidemic prediction model could identify the future tendency of Echinococcosis outbreak [19].
Table 1.
Summary of studies on the prediction of epidemic diseases using grey prediction models.
| Reference | Disease | Method(s) | Country |
|---|---|---|---|
| Gao et al. [13] | Malaria | GM (1,1) | China |
| Ding et al. [14] | H1N1 | GM (1,1), D-R algorithm | China |
| Ren et al. [15] | Tuberculosis | GM (1,1), D-R algorithm | US, Germany |
| Shen et al. [16] | TPF | GM (1,1), DGM | China |
| Guo et al. [17] | Dysentery and Gonorrhea | GM (1,1), SMGM (1,1), and Linear Model | China |
| Zhang et al. [18] | HBV | GM (1,1), GVM, NGBM (1,1), PSO-NNGBM (1,1), and HWES | China |
| Zhang et al. [19] | Echinococcosis | GM (1,1), PECGM (1,1), FGM (1,1), and SARIMA | China |
| Yang et al. [20] | TPF | GM (1,1) | China |
| Wang et al. [21] | HBV | GM (1,1), ARIMA | China |
| Gao et al. [22] | TPF | GM (1,1), SARIMA | China |
| Şahin and Şahin [23] | COVID-19 | GM (1,1), NGBM (1,1), and FANGBM (1,1) | Italy, UK, and the USA |
| Luo et al. [24] | COVID-19 | GM (1,1), GVM, ARGM (1,1), ONGM (1,1), ENGM (1,1), ARIMA, NGBM (1,1), GRM (1,1), and GERM (1,1, ) | China, Italy, Britain, and Russia |
| Zhao et al. [25] | COVID-19 | Rolling-GVM | China |
| This study | COVID-19 | GM (1,1), Rolling-GM (1,1), Rolling-PSO-GM (1,1), and NARNN | Germany, Turkey, and the USA |
H1N1: Influenza A Virus Subtype; HBV: Hepatitis B Virus; TPF: Typhoid and Paratyphoid Fevers; DGM: Discrete Grey Model; SMGM(1,1): GM(1,1) model with self-memory principle; GVM: Grey Verhulst Model; NGBM(1,1): Nonlinear Grey Bernoulli Model; PSO-NNGBM(1,1): Nash Nonlinear Grey Bernoulli Model Optimized by Particle Swarm Optimization; HWES: Holt–Winters Exponential Smoothing; PECGM(1,1): Grey-Periodic Extensional Combinatorial Model; FGM(1,1): Modified Grey Model using Fourier Series; ARIMA: Autoregressive Integrated Moving Average; SARIMA: Seasonal Autoregressive Integrated Moving Average; FANGBM(1,1): Fractional Nonlinear Grey Bernoulli Model; ARGM(1,1): Autoregressive Grey Model; ONGM(1,1): Optimized NGM(1,1,k,c) Model; ENGM(1,1): Exact Nonhomogeneous Grey Model; GRM(1,1): Grey Richards Model; GERM(1,1,): Grey Extend Richards Model; Rolling-GVM: Grey Verhulst Models with a Rolling Mechanism; NARNN: Nonlinear Autoregressive Neural Network; Rolling-GM(1,1): GM(1,1) Model with a Rolling Mechanism; Rolling-PSO-GM(1,1): Grey Modelling (1,1) Optimized by Particle Swarm Optimization with a Rolling Mechanism, COVID-19: Coronavirus Disease 2019.
Yang et al. (2018) applied the GM (1,1) model on the prediction of the incidence trend of typhoid and paratyphoid fevers in Wuhan, China, to help decision-makers to take measures on prevention and control [20]. Wang et al. (2018) compared the success of the GM (1,1) model with the Autoregressive Integrated Moving Average (ARIMA) model for the prediction of hepatitis B in China [21]. Gao et al. (2020) analysed the long-term cumulative incidence of both typhoid and paratyphoid fevers in China using both GM (1,1) and Seasonal Autoregressive Integrated Moving Average (SARIMA) models [22]. Şahin and Şahin (2020) [23], Luo et al. (2020) [24], and Zhao et al. (2020) [25] studied the prediction of cumulative COVID-19 cases using grey prediction models.
As shown in Table 1, the grey prediction model is used as a common tool to predict the spread of different epidemics. This can be attributed to the structure of the GM (1,1) model, which can work efficiently with less data. Despite its wide use, the prediction efficiency of the traditional GM (1,1) model is still being improved [26]. The rolling mechanism developed by Akay and Atak (2007) is one of the most effective methods used to increase the predictive ability of the GM (1,1) model [27]. It includes the use of recent data to handle noisy sequences. Thus, the rolling mechanism was used in this study, as recent data represents the latest epidemiological trend and characteristic of the epidemic. Besides, the classical GM (1,1) parameters were optimized using Particle Swarm Optimization (PSO), a meta-heuristic algorithm inspired by nature. The main reason for using the PSO algorithm is to provide an advantage for the Rolling-GM (1,1) model due to its quick convergence nature and finding optimal solutions in a reasonable time [28]. The prediction capability of the grey rolling model optimized by the PSO algorithm, abbreviated as Rolling-PSO-GM (1, 1), was also compared with common prediction models such as Nonlinear Autoregressive Neural Network (NARNN), GM (1, 1), and Rolling-GM (1, 1).
The COVID-19 epidemic has reached a peak in many countries. What we know about the virus is much more than the beginning of the outbreak. For this reason, the forecasting studies based on the data at the onset of the epidemic need to be updated and compared. This study aims to accurately estimate the total number of confirmed COVID-19 cases while still experiencing this virus. To the best of the author’s knowledge, the Rolling-PSO-GM (1,1) model is used for the first time in estimating the number of COVID-19 cases. Thus, this study is expected to contribute to the literature in this respect. Presenting a case study on Turkey, Germany, and the USA, it is believed that this study can be one of can be the promising alternative and guiding studies for estimating the number of COVID-19 cases for other countries. Furthermore, the results of this study are expected to provide effective guidance in the decision-making process for the prevention and control of epidemics for the governments.
2. Material and methods
2.1. Data collection
In this study, the total confirmed cases of COVID-19 in three countries, Germany, Turkey, the USA, were discussed. The COVID-19 data was taken from the Johns Hopkins University website (https://github.com/CSSEGISandData/COVID-19). The 40-day data was divided into two parts: the in-sample dataset and the out-of-sample dataset. Data from April 26, 2020, to May 30, 2020, were used as an in-sample dataset for model construction. On the other hand, data from April 31, 2020, to June 04, 2020, were used as an out-of-sample dataset to determine how well the developed models perform on the new dataset. All analyses were performed using MATLAB version 2019b software.
2.2. Nonlinear autoregressive neural network
The use of linear models makes the problem more burdensome because most of the time-series data include high variability and transient nature [29]. To overcome the limitation of the linear models, nonlinear approaches that recognize time series patterns and nonlinear characteristics of the data are required. Artificial Intelligence (AI) models are frequently used in the literature because they adapt quickly to changes in the system and can successfully predict nonlinear problems [30]. Nonlinear Autoregressive Neural Network (NARNN) is an AI prediction method used to predict next values using historical values of one-dimensional series [31]. It is commonly used in different fields such as wind forecasting [32], global solar radiation forecasting [33], disease prevalence prediction [29], and power prediction [34]. In this study, the NARNN model was built and used for short-term prediction of COVID-19 spread in Germany, Turkey, and the USA. The mathematical representation of the NARNN model can be represented as follows [35]:
| (1) |
where is the current response, is the nonlinear function, and it is approximated during the training stage of the network by calculating the optimal weights of the network and the corresponding bias, are the historical responses, and is the time delay parameter. In the NARNN model, a closed-loop network is used to perform a multi-step prediction. The output of the closed-loop NARNN model is expressed as follows [35]:
| (2) |
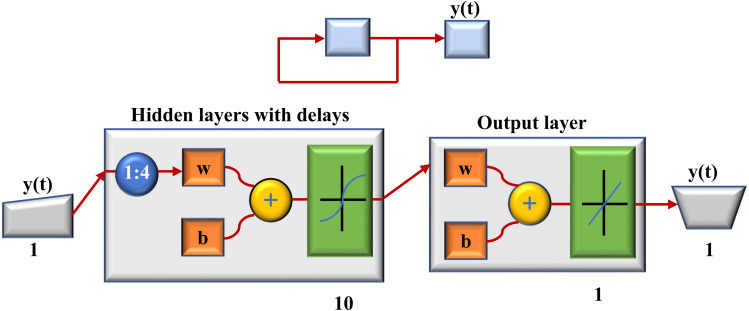
where is the forecast steps in the future. The basic NARNN framework is shown in Fig. 1
Fig. 1.
The structure of the NARNN model.
The NARNN model has a structure consisting of an input layer, an output layer, and several hidden layers. There are two parameters of the model that need to be specified, i.e., delay order and the number of hidden layer nodes.
2.3. Grey prediction model with rolling mechanism
The grey system theory (GST), dealing with systems having uncertain and incomplete information, was proposed by Julong Deng in the 1980s [36]. The grey prediction in the GST is used to investigate a large amount of unknown information using a small amount of information in a system containing incomplete data [37], [38]. In the grey prediction model GM (n,m), n indicates the order of differential equations, and m indicates the number of variables. In terms of easy calculation, the most commonly used model is the GM (1,1) model. The GM (1,1) model represents the first-order model with a single variable. The GM (1,1) model has many advantages compared to traditional prediction methods because it does not require to know if the prediction variables fit the normal distribution, and also not much statistical samples are necessary [20], [39]. Therefore, GM (1,1) model has been used successfully in predicting problems in many disciplines and has achieved very successful results [40]. The grey prediction has three basic operations: the accumulated generating operator (AGO), the inverse accumulating operator (IAGO), and the grey model (GM). The steps of the GM (1,1) model is as follows [41].
Step 1. The non-negative row sequence with n samples is presented in Eq. (3).
| (3) |
Monotonically increasing series is generated by using a one-time accumulating generation operation (1-AGO):
| (4) |
where,
| (5) |
Step 2. A first-order grey differential equation is formed to obtain GM (1,1) model:
| (6) |
where,
| (7) |
where and b are called the developing and the driving coefficient, respectively. is a dynamic parameter in practical applications and is taken as 0.5 in the original GM (1,1) model. These are two parameters of the GM (1,1) model and can be estimated using the least square method :
| (8) |
where is the constant vector, and B is the accumulated matrix.
| (9) |
Step 3. After calculating the a and b coefficients, the GM (1,1) model can be established by solving the differential equation in Eq. (10)
| (10) |
where the initial condition is taken as .
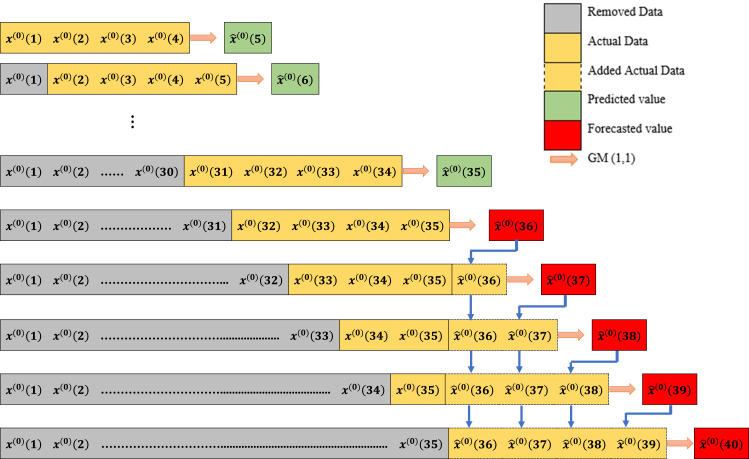
Typically, in the original GM (1,1) model, all data is used for prediction. However, in the case of chaotic data, it is recommended to use the latest data to improve the prediction accuracy of the GM (1,1) model. To achieve this, the grey prediction with a rolling mechanism (Rolling-GM (1,1)) model based on the rolling steps using the last data, removing the old data for each loop, is used [27]. In Rolling-GM (1,1) model, is forecasted by employing the original GM (1,1) model to where . After the result is found, the forecasting procedure is repeated, but the newly estimated entry is added to at the end of the sequence, and the oldest data is removed from the data. Next, is used to predict . Fig. 2 shows the flow chart of the Rolling-GM (1,1) model for this study [42].
Fig. 2.
Forecasting procedure of the Rolling-GM (1,1) model for this study.
2.4. Parameter optimization
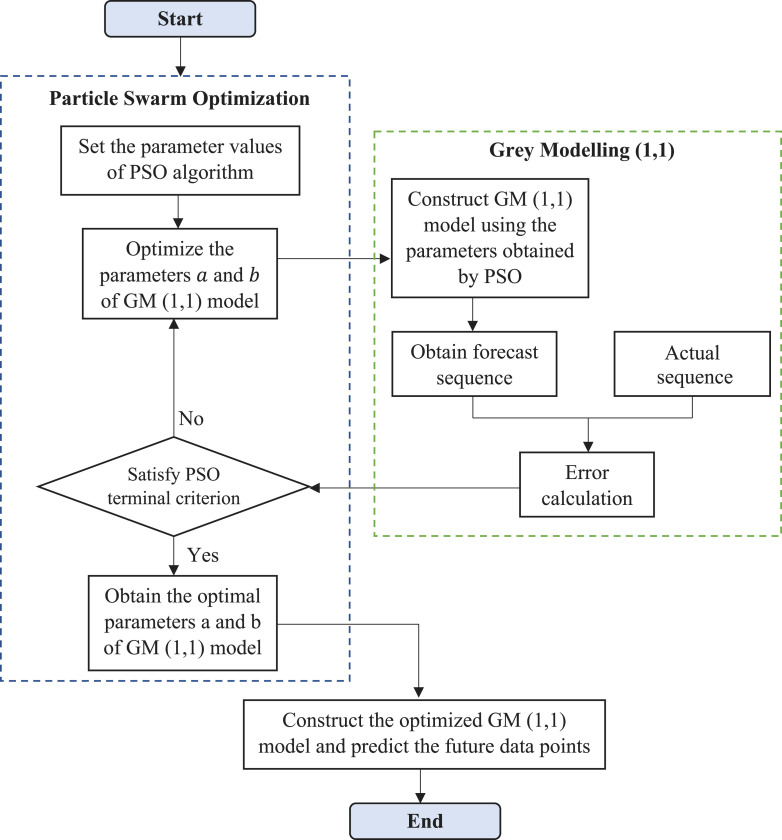
The prediction performance of the GM (1,1) model depends on two parameters calculated in Eq. (8), namely the developing parameter and the driving coefficient . In the classical GM (1,1) model, these parameters are calculated by the least-squares estimation method. However, both of these parameters can also be obtained by intelligent optimization algorithms, which can improve the predictive performance of the classical GM (1,1) model. In this study, the optimal values of the and coefficients in each rolling period were calculated using the PSO algorithm to increase the prediction accuracy of the COVID-19 spread. The optimization process of the and parameters of the GM (1,1) model by PSO algorithm is shown in Fig. 3.
Fig. 3.
Flowchart of GM (1,1) model optimized by PSO algorithm.
2.5. Particle swarm optimization
The Particle Swarm Optimization (PSO), initially proposed by Kennedy and Eberhart [43], is a population-based optimization algorithm used to achieve the optimal solution, inspired by the social behaviour of birds and fish flocking. PSO algorithm has been successfully applied to a variety of real-world applications because of the computational efficiency in solving complex optimization problems and the rapid convergence to a reasonably good solution [44], [45].
In the PSO algorithm, the system starts with a population of random potential solutions, and m particles are generated in the D-dimension solution space randomly. and where , represent the position (direction) and velocity of particles, respectively. Each X position in the flock is scored based on the solution approach to the problem. Personal best (pbest) is the local best of the current generation for each particle; on the other hand, global best (gbest) represents the global best among the local best examples in the current generation. Each particle moves in the direction of its previous best () and the global best () position in the swarm with a certain velocity to find the gbest position. The following Eqs. (11), (12) show how a particle velocity and position are updated [46].
| (11) |
| (12) |
where w represents the inertia weight used to balance the local and global search capabilities of the algorithm, and are the acceleration coefficients representing learning behaviour, enables the particle to benefit from its own experience, provides the experience of partners’ particles in the flock. and are uniform random numbers ranging from 0 to 1, refers to the number of iterations, is the personal best position of the particle i in the dth dimension, position and is the gbest position achieved so far in the flock. In the rest of this study, the developed model is abbreviated as Rolling-PSO-GM (1,1). The details of the PSO algorithm are given as follows.
Table 2.
The parameter values calculated by GM (1,1), Rolling-GM (1,1), and Rolling-PSO-GM (1,1) models.
| Country | Date | GM (1,1) |
Rolling-GM (1,1) |
Rolling-PSO-GM (1,1) |
|||
|---|---|---|---|---|---|---|---|
| a | b | a | b | a | b | ||
| Germany | 31-May | −0.0041 | 160,780.5359 | −0.0027 | 181,532.5496 | −0.0027 | 181,455.2106 |
| 1-June | −0.0023 | 182,242.0345 | −0.0019 | 182,380.4666 | |||
| 2-June | −0.0026 | 182,516.5239 | −0.0019 | 182,747.0767 | |||
| 3-June | −0.0024 | 183,083.9341 | −0.0014 | 183,382.3125 | |||
| 4-June | −0.0025 | 183,457.0084 | −0.0016 | 183,535.6261 | |||
| Turkey | 31-May | −0.01036 | 117,195.8141 | −0.0066 | 159,432.2875 | −0.0064 | 159,452.5876 |
| 1-June | −0.0064 | 160,557.0853 | −0.0062 | 160,592.7040 | |||
| 2-June | −0.0065 | 161,533.6708 | −0.0057 | 161,825.6768 | |||
| 3-June | −0.0064 | 162,620.9347 | −0.0059 | 162,680.5650 | |||
| 4-June | −0.0065 | 163,645.0932 | −0.0059 | 163,679.1199 | |||
| USA | 31-May | −0.0164 | 1,033,121.5836 | −0.0137 | 1,692,244.8785 | −0.0135 | 1,693,002.5918 |
| 1-June | −0.0136 | 1,716,018.1400 | −0.0133 | 1,717,202.3190 | |||
| 2-June | −0.0137 | 1,739,384.9457 | −0.0131 | 1,740,763.5549 | |||
| 3-June | −0.0136 | 1,763,534.7679 | −0.0127 | 1,765,423.0989 | |||
| 4-June | −0.0137 | 1,787,680.8312 | −0.0123 | 1,789,983.3062 | |||
2.6. Performance evaluation metrics
Prediction accuracy is an important criterion for evaluating the performance of a forecasting model. In this study, three metrics were calculated to compare the accuracy and reliability of the models: mean absolute deviation (MAD), root mean square error (RMSE), mean absolute percent error (MAPE%). MAD and RMSE are two metrics of the average magnitude of the forecast errors. MAPE is a general metric considered as a percentage of prediction accuracy. The calculation of MAD, RMSE, and MAPE are given by the following Eqs. (13), (14), (15).
| (13) |
| (14) |
| (15) |
where n is the number of observations, and are actual and predicted data at time k, respectively. It is known that the model with the lowest MAD, MAPE, and RMSE values means better performance.
3. Results
The classic GM (1,1), Rolling-GM (1,1), NARNN models were employed to verify the effectiveness of the Rolling-PSO-GM (1,1) model in estimating the number of confirmed COVID-19 cases in Germany, Turkey, and the USA. In models with a rolling mechanism, a small value of is preferred for the rolling if a prediction series includes a significant versatility [27]. In this case, data from the last four periods (, , , and is selected to forecast point. Therefore, the rolling mechanism in this study was built by selecting the last four days of cumulative COVID-19 cases data. That is, the number of the total confirmed COVID-19 cases for each fifth day is calculated based on the total confirmed data of the previous four days. For example, the total number of COVID-19 cases on April 30 is estimated using data from April 26, 2020, to April 29, 2020. Thus, and parameter values in the Rolling-GM (1, 1) model change at each rolling stage.
On the other hand, the NARNN model was implemented using the Neural Network Toolbox in MATLAB version 2019b software. The 35-day dataset was divided into three main subsets: training (70%25 data), validation (15%5 data), and test set (15%5 data). The delay parameter was set to four to compare the NARNN model results with the grey rolling models. Also, the NARNN model was run five times with a single hidden layer with ten neurons. The traditional Levenberg–Marquardt backpropagation algorithm was used to train the model. This algorithm was chosen because it is known as the fastest backpropagation training algorithm in the literature [29].
For the classical GM (1, 1) model, all COVID-19 data from April 26 to May 30, 2020, was used for the inputs of the grey model, and then the fixed values of parameters and are calculated. For Rolling-PSO-GM (1,1) model, the optimum values of the and parameters were obtained by the PSO algorithm at each rolling stage. Table 2 shows the parameters calculated by the three grey prediction models.
According to the PSO operations steps, the parameters of the PSO algorithm are set as follows: In Eq. (11), and , cognitive and social acceleration coefficients, respectively, are adjusted small () to avoid missing the optimal solution. Besides, the maximum inertia weight was determined as 0.8 based on the study by Shi and Eberhart [32]. The maximum iteration number is set to 2000. All initial parameter values of PSO are given in Table 3.
Table 3.
The initial parameters of the PSO algorithm.
| Parameter | Value |
|---|---|
| Maximum number of iterations (epochs) to train | 2000 |
| Maximum inertia weight, | 0.8 |
| Minimum inertia weight, | 0.1 |
| Acceleration coefficients, | 1 |
| Number of particles | 70 |
| The maximum velocity | 2 |
| Minimum global error gradient |
Table 4 shows the forecasting values of NARNN, GM (1,1), Rolling GM (1,1), and Rolling-PSO-GM (1,1) models used to predict the spread of COVID-19 in countries. To directly compare the performance of classical GM (1,1) with rolling-based forecasting models, the values from April 26 to April 29, 2020, were not taken into account.
Table 4.
Comparison of reported and predicted COVID-19 cases for the countries.
| Date | Germany |
Turkey |
USA |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual | NARNN | GM (1,1) | Rolling- GM (1,1) | Rolling-PSO- GM (1,1) | Actual | NARNN | GM (1,1) | Rolling- GM (1,1) | Rolling-PSO- GM (1,1) | Actual | NARNN | GM (1,1) | Rolling- GM (1,1) | Rolling-PSO- GM (1,1) | |
| In-sample | |||||||||||||||
| 26-Apr | 157,770 | 110,130 | 971,078 | ||||||||||||
| 27-Apr | 158,758 | 112,261 | 994,265 | ||||||||||||
| 28-Apr | 159,912 | 114,653 | 1,018,926 | ||||||||||||
| 29-Apr | 161,539 | 117,589 | 1,046,737 | ||||||||||||
| 30-Apr | 163,009 | 162,819 | 163,748 | 162,871 | 162,948 | 120,204 | 120,534 | 122,709 | 120,265 | 120,347 | 1,076,224 | 1,099,297 | 1,111,092 | 1,073,548 | 1,074,002 |
| 01-May | 164,077 | 163,988 | 164,418 | 164,607 | 164,559 | 122,392 | 122,753 | 123,987 | 123,135 | 123,079 | 1,110,464 | 1,121,550 | 1,129,477 | 1,105,854 | 1,106,259 |
| 02-May | 164,967 | 164,743 | 165,091 | 165,428 | 165,361 | 124,375 | 124,762 | 125,279 | 124,938 | 124,867 | 1,138,228 | 1,148,564 | 1,148,166 | 1,143,081 | 1,143,768 |
| 03-May | 165,664 | 165,485 | 165,767 | 165,985 | 165,951 | 126,045 | 126,496 | 126,584 | 126,550 | 126,520 | 1,162,685 | 1,171,283 | 1,167,164 | 1,171,625 | 1,170,557 |
| 04-May | 166,152 | 166,169 | 166,445 | 166,495 | 166,525 | 127,659 | 128,151 | 127,902 | 127,965 | 127,912 | 1,186,067 | 1,193,261 | 1,186,477 | 1,190,273 | 1,189,709 |
| 05-May | 167,007 | 166,914 | 167,126 | 166,782 | 166,857 | 129,491 | 130,035 | 129,235 | 129,344 | 129,279 | 1,210,577 | 1,216,569 | 1,206,109 | 1,210,939 | 1,210,653 |
| 06-May | 168,162 | 168,150 | 167,810 | 167,622 | 167,683 | 131,744 | 132,085 | 130,581 | 131,216 | 131,239 | 1,235,666 | 1,240,133 | 1,226,066 | 1,235,110 | 1,235,451 |
| 07-May | 169,430 | 169,512 | 168,496 | 169,127 | 169,135 | 133,721 | 134,285 | 131,941 | 133,770 | 133,835 | 1,263,402 | 1,263,741 | 1,246,353 | 1,261,179 | 1,261,608 |
| 08-May | 170,588 | 170,643 | 169,186 | 170,637 | 170,622 | 135,569 | 136,112 | 133,316 | 135,934 | 135,888 | 1,290,151 | 1,290,387 | 1,266,976 | 1,290,288 | 1,290,851 |
| 09-May | 171,324 | 171,341 | 169,878 | 171,833 | 171,792 | 137,115 | 137,729 | 134,704 | 137,546 | 137,503 | 1,315,099 | 1,315,525 | 1,287,941 | 1,318,484 | 1,318,084 |
| 10-May | 171,879 | 170,715 | 170,573 | 172,349 | 172,279 | 138,657 | 139,104 | 136,108 | 138,895 | 138,844 | 1,333,970 | 1,338,717 | 1,309,252 | 1,342,058 | 1,341,652 |
| 11-May | 172,576 | 170,637 | 171,271 | 172,558 | 172,564 | 139,771 | 140,183 | 137,525 | 140,229 | 140,101 | 1,353,397 | 1,355,104 | 1,330,915 | 1,357,438 | 1,356,434 |
| 12-May | 173,171 | 173,191 | 171,971 | 173,182 | 173,210 | 141,475 | 141,887 | 138,958 | 141,189 | 141,118 | 1,376,122 | 1,375,093 | 1,352,938 | 1,372,892 | 1,373,339 |
| 13-May | 174,098 | 174,085 | 172,675 | 173,838 | 173,870 | 143,114 | 142,757 | 140,406 | 142,810 | 142,905 | 1,397,085 | 1,400,335 | 1,375,324 | 1,397,186 | 1,397,695 |
| 14-May | 174,478 | 174,480 | 173,382 | 174,809 | 174,850 | 144,749 | 144,552 | 141,868 | 144,827 | 144,754 | 1,424,243 | 1,419,663 | 1,398,081 | 1,419,764 | 1,420,215 |
| 15-May | 175,233 | 175,264 | 174,091 | 175,226 | 175,135 | 146,457 | 146,889 | 143,346 | 146,416 | 146,433 | 1,449,498 | 1,448,977 | 1,421,215 | 1,447,964 | 1,448,931 |
| 16-May | 175,752 | 175,776 | 174,803 | 175,741 | 175,803 | 148,067 | 148,427 | 144,839 | 148,147 | 148,001 | 1,473,514 | 1,472,656 | 1,444,731 | 1,476,775 | 1,476,611 |
| 17-May | 176,369 | 175,943 | 175,519 | 176,432 | 176,406 | 149,435 | 149,685 | 146,348 | 149,772 | 149,698 | 1,491,829 | 1,493,201 | 1,468,637 | 1,499,013 | 1,498,270 |
| 18-May | 176,551 | 176,552 | 176,237 | 176,924 | 176,732 | 150,593 | 150,741 | 147,873 | 150,987 | 150,927 | 1,513,816 | 1,508,073 | 1,492,938 | 1,514,400 | 1,513,456 |
| 19-May | 177,778 | 175,809 | 176,958 | 177,024 | 176,952 | 151,615 | 151,572 | 149,413 | 151,907 | 151,860 | 1,534,871 | 1,532,351 | 1,517,641 | 1,533,803 | 1,534,378 |
| 20-May | 178,473 | 176,656 | 177,682 | 178,314 | 178,487 | 152,587 | 152,462 | 150,969 | 152,740 | 152,664 | 1,557,933 | 1,554,757 | 1,542,753 | 1,557,028 | 1,557,203 |
| 21-May | 179,021 | 179,019 | 178,409 | 179,530 | 179,442 | 153,548 | 153,435 | 152,542 | 153,603 | 153,565 | 1,583,798 | 1,578,484 | 1,568,280 | 1,580,169 | 1,581,012 |
| 22-May | 179,710 | 180,489 | 179,139 | 179,670 | 179,701 | 154,500 | 154,444 | 154,131 | 154,526 | 154,481 | 1,607,109 | 1,606,756 | 1,594,230 | 1,608,418 | 1,608,141 |
| 23-May | 179,986 | 179,994 | 179,872 | 180,309 | 180,256 | 155,686 | 155,437 | 155,737 | 155,467 | 155,550 | 1,628,212 | 1,628,082 | 1,620,609 | 1,632,715 | 1,632,168 |
| 24-May | 180,328 | 180,348 | 180,608 | 180,539 | 180,470 | 156,827 | 156,407 | 157,359 | 156,728 | 156,796 | 1,648,158 | 1,646,710 | 1,647,425 | 1,651,264 | 1,650,785 |
| 25-May | 180,600 | 180,597 | 181,347 | 180,627 | 180,594 | 157,814 | 157,503 | 158,998 | 158,012 | 157,874 | 1,666,505 | 1,666,766 | 1,674,684 | 1,669,281 | 1,668,453 |
| 26-May | 181,200 | 180,716 | 182,089 | 180,919 | 181,039 | 158,762 | 158,331 | 160,655 | 158,915 | 158,876 | 1,685,956 | 1,685,503 | 1,702,394 | 1,686,265 | 1,686,034 |
| 27-May | 181,524 | 181,558 | 182,834 | 181,583 | 181,601 | 159,797 | 159,416 | 162,328 | 159,745 | 159,777 | 1,704,489 | 1,706,408 | 1,730,563 | 1,705,015 | 1,704,499 |
| 28-May | 182,196 | 182,195 | 183,582 | 182,034 | 182,052 | 160,979 | 160,550 | 164,019 | 160,784 | 160,897 | 1,727,357 | 1,726,176 | 1,759,198 | 1,723,970 | 1,725,182 |
| 29-May | 182,922 | 182,823 | 184,333 | 182,638 | 182,700 | 162,120 | 161,517 | 165,728 | 162,076 | 162,117 | 1,751,612 | 1,750,280 | 1,788,307 | 1,747,751 | 1,748,437 |
| 30-May | 183,189 | 183,264 | 185,087 | 183,616 | 183,367 | 163,103 | 162,359 | 167,454 | 163,302 | 163,172 | 1,775,428 | 1,774,423 | 1,817,898 | 1,775,458 | 1,775,591 |
| Out-of-sample | |||||||||||||||
| 31-May | 183,410 | 183,538 | 185,844 | 183,764 | 183,688 | 163,942 | 163,093 | 169,199 | 164,202 | 164,139 | 1,794,465 | 1,793,849 | 1,847,978 | 1,800,058 | 1,799,322 |
| 01-Jun | 183,594 | 183,421 | 186,605 | 184,135 | 183,959 | 164,769 | 164,006 | 170,961 | 165,234 | 165,096 | 1,811,393 | 1,806,855 | 1,878,556 | 1,824,673 | 1,823,222 |
| 02-Jun | 183,879 | 183,223 | 187,368 | 184,644 | 184,289 | 165,555 | 164,579 | 172,742 | 166,322 | 166,023 | 1,832,782 | 1,814,934 | 1,909,639 | 1,849,832 | 1,846,742 |
| 03-Jun | 184,121 | 183,057 | 188,135 | 185,063 | 184,500 | 166,422 | 167,017 | 174,542 | 167,384 | 167,062 | 1,852,788 | 1,820,198 | 1,941,237 | 1,875,169 | 1,869,405 |
| 04-Jun | 184,472 | 182,724 | 188,904 | 185,544 | 184,824 | 167,410 | 165,874 | 176,360 | 168,474 | 168,042 | 1,874,156 | 1,823,506 | 1,973,358 | 1,900,935 | 1,891,680 |
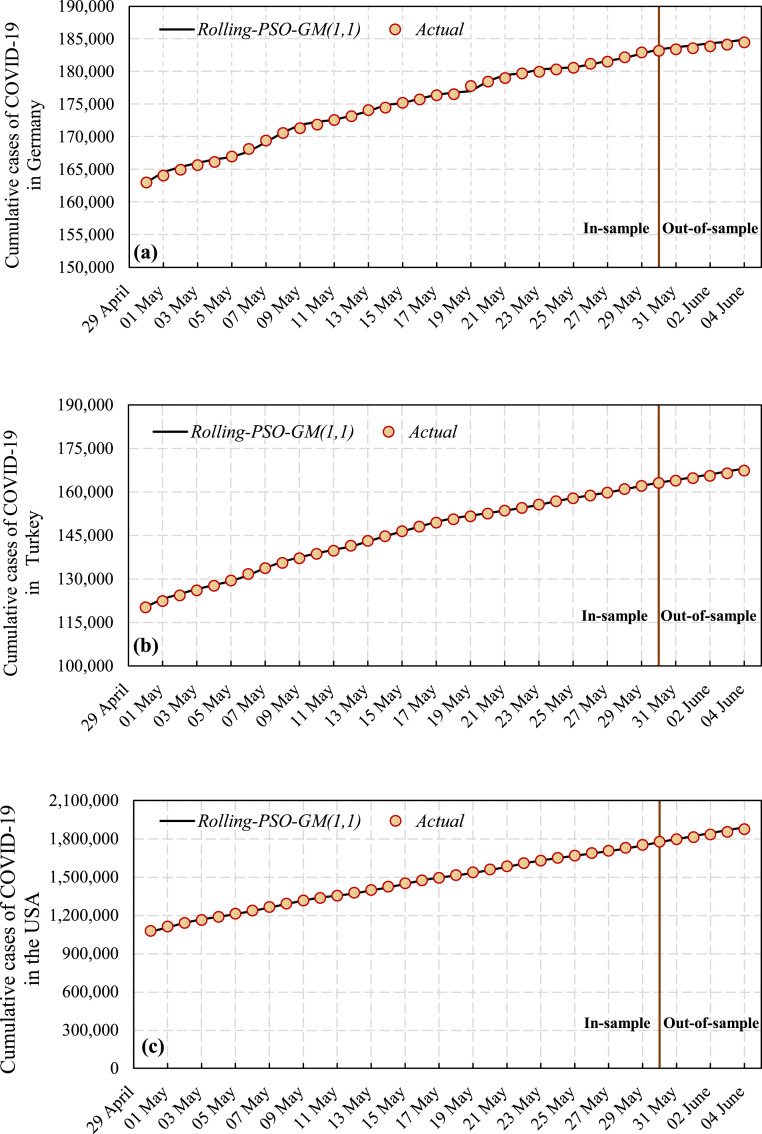
As seen in Table 4, the Rolling-GM (1,1) and Rolling-PSO-GM (1,1) models outperform the original GM (1, 1) model for all countries. On the other hand, in terms of prediction errors, the NARNN achieved better prediction results than the classical GM (1, 1) model. However, it performed worse than the Rolling-GM (1, 1) and Rolling-PSO-GM (1, 1) models. The main reason for this may be that the rolling-based prediction models have a mechanism that updates the data at each rolling stage. It is seen that the PSO algorithm has significantly improved the prediction performance of the Rolling-GM (1,1) model in both model building and model testing stages. This shows that optimizing the and parameters can improve the prediction accuracy of the grey model. Fig. 4 presents the forecasting results of the cumulative cases of COVID-19 for Germany, Turkey, and the USA using Rolling-PSO-GM (1,1) model, respectively. There appears to be good agreement between the reported confirmed cases and the predicted cases.
Fig. 4.
Actual and predicted values of COVID-19 data in (a) Germany, (b) Turkey, and (c) the USA.
From Table 5, it is seen that the lowest MAD, RMSE, and MAPE (%) values of the Rolling-PSO-GM (1,1) model for Germany are 222.935, 292.748, and 0.129% in the sample dataset and 356.800, 359.487, and 0.194% in the out-of-sample dataset, respectively. It also performs best with the values of MAD 201.161, RMSE 266.677, and MAPE 0.148% in the sample dataset and MAD 452.800, RMSE 484.517, and MAPE 0.273% in the out-of-sample dataset of Turkey. Similarly, it has the best performance for the USA with the values MAD 2484.806, RMSE 3292.779, and MAPE 0.184% in the sample dataset and MAD 12 957.400, RMSE 13 723.065, and MAPE 0.703% in the out-of-sample dataset. Clearly, the analysis results confirm that the Rolling-PSO-GM (1,1) is more accurate and provides a significant improvement over the NARNN, traditional GM (1,1), and Rolling-GM (1,1) models.
Table 5.
The performance evaluation metrics to compare NARNN, GM (1,1), Rolling-GM (1,1), and Rolling-PSO-GM (1,1) models.
| Country | Performance criteria | NARNN | GM (1,1) | Rolling- GM (1,1) | Rolling-PSO- GM (1,1) |
|---|---|---|---|---|---|
| In-sample (26 April–30 May) | |||||
| Germany | MAD | 318.355 | 847.323 | 264.484 | 222.935 |
| RMSE | 659.427 | 977.334 | 328.544 | 292.748 | |
| MAPE (%) | 0.182 | 0.482 | 0.153 | 0.129 | |
| Turkey | MAD | 372.484 | 1970.355 | 245.129 | 201.161 |
| RMSE | 407.328 | 2253.889 | 304.895 | 266.677 | |
| MAPE (%) | 0.262 | 1.353 | 0.177 | 0.148 | |
| USA | MAD | 3698.258 | 19 369.065 | 2898.677 | 2484.806 |
| RMSE | 5937.719 | 21 968.532 | 3702.010 | 3292.779 | |
| MAPE (%) | 0.296 | 1.347 | 0.212 | 0.184 | |
| Out-of-sample (31 May–4 June) | |||||
| Germany | MAD | 753.800 | 3476.000 | 734.800 | 356.800 |
| RMSE | 965.841 | 3547.349 | 779.714 | 359.487 | |
| MAPE (%) | 0.409 | 1.889 | 0.399 | 0.194 | |
| Turkey | MAD | 943.800 | 7141.200 | 703.600 | 452.800 |
| RMSE | 996.882 | 7261.774 | 765.461 | 484.517 | |
| MAPE (%) | 0.569 | 4.306 | 0.424 | 0.273 | |
| USA | MAD | 21 248.400 | 77 036.800 | 17 016.600 | 12 957.400 |
| RMSE | 28 167.551 | 78 671.177 | 18 527.636 | 13 723.065 | |
| MAPE (%) | 1.144 | 4.190 | 0.922 | 0.703 | |
4. Discussion
The grey system theory requires only a limited number of data to understand the behaviour of unknown systems that differ from other time-series methods. The grey prediction models are widely used for short-term prediction due to the simple calculation ability and higher predictive accuracy. In recent years, grey modelling (1,1) has become increasingly popular in both medicine and public health research. Therefore, in this study, a hybrid model based on grey modelling (1,1) and rolling mechanism optimized by the PSO was used for short-term prediction of COVID-19 spread.
The study results can give information about the estimated number of COVID-19 cases that may occur in the next few days. Since the outbreak started on different dates in different countries, viewing the curve of each country allows us to compare countries more easily. Comparisons between countries can provide preliminary information about where and how the pandemic grew at any given time.
According to results obtained by the Rolling-PSO-GM (1,1) model, the number of confirmed new cases is expected to be an average of 303, 988, and 23 250 cases in the next five days (31 May-4 June) for Germany, Turkey, and the USA, respectively. Germany is one of the first countries to develop a reflex against the epidemic, and it has seen a consistent drop in new cases. On the other hand, the total number of COVID-19 continues to increase in the USA, where COVID-19 causes approximately 112,000 deaths, respectively. The country’s health system is struggling to cope with the epidemic. The estimates indicate that the current trend is far behind Germany and Turkey. In all three countries, comprehensive prevention and control are required to be maintained and strengthened to reduce the spread of COVID-19.
The present study should be interpreted in light of some limitations. The used data in this study was taken from the official website of Johns Hopkins University. It includes positive cases are that have been confirmed by the state, national or local labs. However, it is difficult to estimate the actual spread of COVID-19 with this information. Because it is more accurate and reliable to say that there are more cases in these countries that have not yet been detected. Thus, it was assumed that the report data in this study might be slightly less than the actual number of cases of COVID-19.
5. Conclusion
There is limited data on the growth trajectory of the COVID-19 outbreak. Besides, the epidemiological features of the new coronavirus are not fully disclosed. Therefore, the prediction of the COVID-19 spread is essential in that it gives an idea of what might happen next days. Public health professionals and policymakers need estimates when making important decisions. These decisions include how to best utilize resources within a health system, which social distancing measures to implement, and what other measures can be taken to reduce the impact of COVID-19. The forecasts provide preliminary information that shows what might happen in the coming days and whether preventive measures are working. However, traditional methods show limitations such as large amounts of statistical data and a structural system requirement. These pose a significant challenge for researchers to predict the spread of COVID-19 accurately. To overcome the problem, the grey system theory was adopted in predicting the spread of COVID-19 in this study.
The GM (1,1), Rolling-GM (1,1), and Rolling-PSO-GM (1,1) models were used to predict the cumulative case number of COVID-19 in Germany, Turkey, and the USA. Besides, the NARNN model, a neural-based forecasting technique, was also implemented to compare the performance of the developed grey models. Analysis results showed that the use of the rolling mechanism and PSO algorithm with the classical GM (1,1) model has significantly improved the prediction accuracy of the COVID-19 spread. Therefore, the Rolling-PSO-GM (1,1) is selected as the best prediction model with having the lowest prediction errors for all countries. However, the Rolling-PSO-GM (1,1) model cannot take into account the economic and social factors affecting the spread of COVID-19. Also, the effect of climate change was ignored for short-term predictions. These disadvantages can be prevented by using the GM (1, n) model, which can be an important research topic in future studies. Besides, in future studies, the parameters of the classical grey prediction model can be optimized using other techniques such as genetic algorithm or the grey wolf optimizer. Thus, the performance of optimization techniques on the short-term prediction of COVID-19 spread can be compared, and different results can be obtained.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
References
- 1.Sohrabi C., Alsafi Z., Neill N.O., Khan M., Kerwan A., Al-jabir A., Iosifidis C., Agha R. World health organization declares global emergency: A review of the 2019 novel coronavirus ( COVID-19 ) Int. J. Surg. 2019;76(2020):71–76. doi: 10.1016/j.ijsu.2020.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ceylan Z. Estimation of COVID-19 prevalence in Italy, Spain, and France. Sci. Total Environ. 2020;729 doi: 10.1016/j.scitotenv.2020.138817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.You C., Deng Y., Hu W., Sun J., Lin Q., Zhou F., Pang C.H., Zhang Y., Chen Z., Zhou X.-H. Estimation of the time-varying reproduction number of COVID-19 outbreak in China. Int. J. Hyg. Environ. Health. 2020;228 doi: 10.1016/j.ijheh.2020.113555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ceylan Z. Insights into the relationship between weather parameters and COVID-19 outbreak in lombardy. Int. J. Healthc. Manag. 2021;14(1):255–263. doi: 10.1080/20479700.2020.1858394. [DOI] [Google Scholar]
- 5.Tomar A., Gupta N. Prediction for the spread of COVID-19 in India and effectiveness of preventive measures. Sci. Total Environ. 2020;728 doi: 10.1016/j.scitotenv.2020.138762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhao Z., Li X., Liu F., Zhu G., Ma C., Wang L. Prediction of the COVID-19 spread in african countries and implications for prevention and controls: A case study in South Africa, Egypt, Algeria, Nigeria, Senegal and Kenya. Sci. Total Environ. 2020;729 doi: 10.1016/j.scitotenv.2020.138959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Maleki M., Reza M., Wraith D., Pho K. Time series modelling to forecast the confirmed and recovered cases of. Travel Med. Infect. Dis. 2020 doi: 10.1016/j.tmaid.2020.101742. [DOI] [PubMed] [Google Scholar]
- 8.P.Ã. Zhou, B.W. Ang, K.L. Poh, A trigonometric grey prediction approach to forecasting electricity demand, Vol .31 (2006) pp. 2839–2847 10.1016/j.energy.2005.12.002. [DOI]
- 9.Xie M., Wu L., Li B., Li Z. A novel hybrid multivariate nonlinear grey model for forecasting the traffic-related emissions. Appl. Math. Model. 2020;77:1242–1254. doi: 10.1016/j.apm.2019.09.013. [DOI] [Google Scholar]
- 10.Ding S., Hipel K.W., Dang Y. Forecasting China’s electricity consumption using a new grey prediction model. Energy. 2018;149:314–328. doi: 10.1016/J.ENERGY.2018.01.169. [DOI] [Google Scholar]
- 11.Chang C., Li D., Huang Y., Chen C. A novel gray forecasting model based on the box plot for small manufacturing data sets. Appl. Math. Comput. 2015;265:400–408. doi: 10.1016/j.amc.2015.05.006. [DOI] [Google Scholar]
- 12.Wang Y., Chen X., Han Y., Guo S. Forecast of passenger and freight traffic volume based on elasticity coefficient method and grey model. Procedia - Soc. Behav. Sci. 2013;96:136–147. doi: 10.1016/j.sbspro.2013.08.019. [DOI] [Google Scholar]
- 13.Gao S., Liu J., Zhang R., Gen Y., Huang D., Wu S. Establishment and estimation of a GM (1, 1) grey model for forecasting of malaria epidemic situation in shenzhen longgang areas. J Pathog. Biol. 2007;2:357–359. [Google Scholar]
- 14.Ding F., Zarlenga D.S., Qin C., Ren X. A novel algorithm to define infection tendencies in H1n1 cases in mainland China. Infect. Genet. Evol. 2011;11:222–226. doi: 10.1016/j.meegid.2010.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Y. Ren, F. Ding, S. Suo, R. Bu, D.S. Zarlenga, X. Ren, Incidence Rates and Deaths of Tuberculosis in HIV- Negative Patients in the United States and Germany as Analyzed by New Predictive Model for Infection, Vol. 7 (2015) pp. 1–6 10.1371/journal.pone.0042055. [DOI] [PMC free article] [PubMed]
- 16.X. Shen, L. Ou, X. Chen, X. Zhang, X. Tan, The Application of the Grey Disaster Model to Forecast Epidemic Peaks of Typhoid and Paratyphoid Fever in China, Vol. 8 (2013) pp. 1–6 10.1371/journal.pone.0060601. [DOI] [PMC free article] [PubMed]
- 17.Guo X., Liu S., Wu L., Tang L. 2014. Application of a novel grey self-memory coupling model to forecast the incidence rates of two notifiable diseases in China: Dysentery and gonorrhea; pp. 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang L., Zheng Y., Wang K., Zhang X., Zheng Y. An optimized Nash nonlinear grey Bernoulli model based on particle swarm optimization and its application in prediction for the incidence of hepatitis b in xinjiang, China. Comput. Biol. Med. 2014;49:67–73. doi: 10.1016/j.compbiomed.2014.02.008. [DOI] [PubMed] [Google Scholar]
- 19.Zhang L., Wang L., Zheng Y., Wang K., Zhang X., Zheng Y. Time prediction models for echinococcosis based on gray system theory and epidemic dynamics. Int. J. Environ. Res. Public Health. 2017;14 doi: 10.3390/ijerph14030262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yang X., Zou J., Kong D., Jiang G. The analysis of GM (1, 1) grey model to predict the incidence trend of typhoid and paratyphoid fevers in wuhan city, China. Medicine (Baltimore) 2018;97 doi: 10.1097/MD.0000000000011787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang Y.-W., Shen Z.-Z., Jiang Y. Comparison of arima and gm(1,1) models for prediction of hepatitis b in China. PLoS One. 2018;13 doi: 10.1371/journal.pone.0201987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gao J., Li J., Id M.W. 2020. Time series analysis of cumulative incidences of typhoid and paratyphoid fevers in China using both grey and SARIMA models; pp. 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Şahin U., Şahin T. Forecasting the cumulative number of confirmed cases of COVID-19 in Italy, UK and USA using fractional nonlinear grey Bernoulli model. Chaos Solitons Fractals. 2020;138 doi: 10.1016/j.chaos.2020.109948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Luo X., Duan H., Xu K. A novel grey model based on traditional richards model and its application in COVID-19. Chaos Solitons Fractals. 2020 doi: 10.1016/j.chaos.2020.110480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhao Y., Shou M., Wang Z. 2020. Prediction of the number of patients infected with COVID-19 based on rolling grey verhulst models. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhao H., Zhao H., Guo S. 2016. Applied sciences using GM (1, 1) optimized by MFO with rolling mechanism to forecast the electricity consumption of. [DOI] [Google Scholar]
- 27.Akay D., Atak M. Grey prediction with rolling mechanism for electricity demand forecasting of Turkey. Energy. 2007;32:1670–1675. doi: 10.1016/j.energy.2006.11.014. [DOI] [Google Scholar]
- 28.W. Ma, X. Zhu, M. Wang, Forecasting iron ore import and consumption of China using grey model optimized by particle swarm optimization algorithm, Vol. 38 (2013) pp. 613–620.
- 29.Saba A.I., Elsheikh A.H. Forecasting the prevalence of COVID-19 outbreak in Egypt using nonlinear autoregressive artificial neural networks. Process Saf. Environ. Prot. 2020;141:1–8. doi: 10.1016/j.psep.2020.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ceylan Z., Sungur B. Estimation of coal elemental composition from proximate analysis using machine learning techniques. Energy Sources A Recover. Util. Environ. Eff. 2020;42:2576–2592. [Google Scholar]
- 31.Benmouiza K., Cheknane A. 2016. Small-scale solar radiation forecasting using arma and nonlinear autoregressive neural network models; pp. 945–958. [DOI] [Google Scholar]
- 32.Ahmed A., Khalid M. Multi-step ahead wind forecasting using nonlinear autoregressive neural networks. Energy Proc. 2017;134:192–204. doi: 10.1016/j.egypro.2017.09.609. [DOI] [Google Scholar]
- 33.Benmouiza K., Cheknane A. Forecasting hourly global solar radiation using hybrid k -means and nonlinear autoregressive neural network models. Energy Convers. Manag. 2013;75:561–569. doi: 10.1016/j.enconman.2013.07.003. [DOI] [Google Scholar]
- 34.Rogier J.K., Mohamudally N. Forecasting photovoltaic power generation via an IoT network using nonlinear autoregressive neural network. Procedia Comput. Sci. 2019;151:643–650. doi: 10.1016/j.procs.2019.04.086. [DOI] [Google Scholar]
- 35.Khaleghi S., Karimi D., Beheshti S.H., Hosen S., Behi H., Berecibar M., Van Mierlo J. Online health diagnosis of lithium-ion batteries based on nonlinear autoregressive neural network. Appl. Energy. 2021;282 doi: 10.1016/j.apenergy.2020.116159. [DOI] [Google Scholar]
- 36.Deng J. Introduction to grey system. J. Grey Syst. 1989;1:1–24. [Google Scholar]
- 37.Lin Y., Chen M.Y., Liu S. Theory of grey systems: Capturing uncertainties of grey information. Kybernetes. 2004;33:196–218. doi: 10.1108/03684920410514139. [DOI] [Google Scholar]
- 38.Ding S., Xu N., Ye J., Zhou W., Zhang X. Estimating chinese energy-related CO2 emissions by employing a novel discrete grey prediction model. J. Clean. Prod. 2020;259 doi: 10.1016/j.jclepro.2020.120793. [DOI] [Google Scholar]
- 39.Hu Y.C. Electricity consumption prediction using a neural-network-based grey forecasting approach. J. Oper. Res. Soc. 2017;68:1259–1264. doi: 10.1057/s41274-016-0150-y. [DOI] [Google Scholar]
- 40.Wu W., Ma X., Zhang Y., Li W., Wang Y. Science of the total environment a novel conformable fractional nonhomogeneous grey model for forecasting carbon dioxide emissions of BRICS countries. Sci. Total Environ. 2020;707 doi: 10.1016/j.scitotenv.2019.135447. [DOI] [PubMed] [Google Scholar]
- 41.Liu S., Lin Y. Grey Information: Theory and Practical Applications. Springer-Verlag; Berlin, Heidelberg: 2005. (Advanced Information and Knowledge Processing). [Google Scholar]
- 42.Şahin U. Forecasting of Turkey’s greenhouse gas emissions using linear and nonlinear rolling metabolic grey model based on optimization. J. Clean. Prod. 2019;239 doi: 10.1016/j.jclepro.2019.118079. [DOI] [Google Scholar]
- 43.Kennedy J., Eberhart R. Part. Swarm Optim. 1995:1942–1948. [Google Scholar]
- 44.Chouikhi N., Ammar B., Rokbani N., Alimi A.M. PSO-Based analysis of echo state network parameters for time series forecasting. Appl. Soft Comput. J. 2017;55:211–225. doi: 10.1016/j.asoc.2017.01.049. [DOI] [Google Scholar]
- 45.Ceylan Z., Pekel E., Ceylan S., Bulkan S. Biomass higher heating value prediction analysis by ANFIS, PSO- ANFIS and GA-ANFIS. Glob. Nest J. 2018;20:589–597. [Google Scholar]
- 46.Ervural B.C. 2019. Improvement of grey prediction models and their usage for energy demand forecasting. [DOI] [Google Scholar]